Риски банков: новый взгляд на оценку потерь

Автор: Денис Аветисян

В статье предлагается усовершенствованный подход к измерению банковских рисков, позволяющий более точно оценивать потенциальные убытки и повышать стабильность финансовой системы.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Кредитный риск в банковском секторе демонстрирует экстремальные потери, оцениваемые с использованием $VaR_{99.9\%}$ и $ES_{99.9\%}$, что позволяет выявить наиболее уязвимые участки распределения убытков.

Предлагается расширение частотно-тяжестной модели оценки рисков до трехточечного распределения, основанное на методах оптимального транспорта и квантования.

Несмотря на десятилетия исследований в области управления рисками, существующие подходы часто сводятся к скалярным показателям, упуская из виду многомерную природу потенциальных потерь. В данной работе, ‘Informative Risk Measuresin the Banking Industry: A Proposal based on the Magnitude-Propensity Approach’, предлагается новый многомерный подход к оценке рисков, основанный на расширении классической модели частоты и тяжести убытков, который позволяет более адекватно отразить структуру возможных потерь портфеля. Предложенная методика, использующая трехточечное распределение вероятностей, обеспечивает повышенную интерпретируемость и устойчивость по сравнению с традиционными мерами, такими как VaR и Expected Shortfall. Сможет ли предложенный подход стать основой для разработки более эффективных систем управления рисками в банковской сфере и повысить их устойчивость к экстремальным событиям?

За пределами традиционных рисков: ограничения VaR

На протяжении многих лет, Value at Risk (VaR) являлся ключевым инструментом в управлении рисками, однако всё больше признаётся его ограниченность в оценке так называемых «хвостовых» рисков — событий с крайне низкой вероятностью, но потенциально катастрофическими последствиями. Эта метрика, основанная на статистических предположениях о нормальном распределении, зачастую недооценивает вероятность экстремальных убытков, особенно в сложных инвестиционных портфелях, подверженных нелинейным зависимостям. В результате, полагаясь исключительно на VaR, организации могут столкнуться с недостаточным объёмом капитала для покрытия реальных потерь в периоды повышенной волатильности или кризисных ситуаций. Неспособность адекватно учитывать «хвостовые» риски становится всё более очевидной в контексте растущей финансовой нестабильности и усложнения рыночных процессов, что стимулирует поиск и внедрение более совершенных методов оценки рисков.

Расчет ценности под риском (VaR) часто основывается на предположении о нормальном распределении доходностей активов и линейной зависимости между компонентами портфеля. Однако, в реальности, финансовые рынки демонстрируют отклонения от нормальности, а взаимосвязи между активами могут быть нелинейными, особенно в периоды турбулентности. Это приводит к тому, что VaR может недооценивать потенциальные убытки в сложных портфелях, состоящих из производных инструментов, опционов или активов с высокой степенью корреляции. Недооценка рисков, в свою очередь, ведет к недостаточному резервированию капитала, что ставит финансовые институты в уязвимое положение перед непредвиденными рыночными шоками и может привести к серьезным финансовым потерям. Таким образом, при использовании VaR необходимо учитывать ограничения, связанные с упрощающими предположениями, и дополнять его другими методами оценки рисков, учитывающими “хвостовые” события и нелинейные зависимости.

Недостаточность традиционных метрик риска, таких как Value at Risk (VaR), в адекватном отражении реального распределения убытков стимулирует поиск более надежных и всеобъемлющих методов оценки. Современные исследования показывают, что стандартные модели часто упрощают сложность финансовых рынков, недооценивая вероятность экстремальных, но потенциально катастрофических потерь. Альтернативные подходы, такие как ожидаемый дефицит (Expected Shortfall, ES) и стресс-тестирование, направлены на более точное моделирование «хвоста» распределения убытков, учитывая не только вероятность наступления неблагоприятного события, но и величину ожидаемых потерь в случае его реализации. Внедрение этих усовершенствованных инструментов позволяет финансовым институтам более эффективно управлять рисками и обеспечивать достаточный уровень капитала для защиты от непредвиденных обстоятельств, что особенно важно в условиях растущей волатильности и взаимосвязанности финансовых рынков.

Традиционные методы оценки рисков зачастую испытывают трудности при одновременном учете частоты и величины потенциальных потерь. Анализ, сконцентрированный исключительно на вероятности наступления неблагоприятного события или же на максимальной возможной сумме убытков, упускает из виду сложную взаимосвязь между этими двумя факторами. Например, редкие, но крайне масштабные потери могут быть недооценены, если система ориентирована на более частые, но менее значительные риски. Подобный подход не позволяет сформировать адекватное представление о полной картине возможных убытков и, как следствие, может привести к неоптимальному распределению капитала и недостаточной готовности к экстремальным событиям. Более современные методики стремятся к комплексному анализу, учитывающему как вероятность, так и размер потенциальных потерь, что позволяет получить более реалистичную и полную оценку рисков.

Распределение убытков показывает риски страхового рынка, оцениваемые по показателям VaR 99.5% и ES 99.5% в хвостовой части.

Когерентные меры риска и продвинутые техники

Когерентные меры риска, такие как Expected Shortfall (ES), также известные как Conditional Value-at-Risk (CVaR), представляют собой более теоретически обоснованный подход к количественной оценке риска по сравнению с Value-at-Risk (VaR). VaR имеет недостатки, включая несоблюдение принципа суб-аддитивности, что может приводить к недооценке риска в портфелях с нелинейными позициями или при наличии зависимостей между активами. Когерентные меры, напротив, удовлетворяют аксиомам, гарантирующим согласованность и рациональность, таким как суб-аддитивность, монотонность, положительная гомогенность и трансляционная инвариантность. Это обеспечивает более надежную основу для принятия решений, связанных с риском, и более точную оценку потенциальных убытков, особенно в сложных финансовых сценариях.

Когерентные меры риска, такие как Expected Shortfall (ES), отличаются от Value-at-Risk (VaR) тем, что удовлетворяют ключевым аксиомам, обеспечивающим согласованность и рациональность при оценке риска. К этим аксиомам относятся монотонность (увеличение убытков при увеличении вероятности их наступления), суб-аддитивность (совокупный риск портфеля не превышает сумму рисков отдельных позиций), положительная гомогенность (пропорциональное увеличение убытков при пропорциональном увеличении размера позиции) и трансляционная инвариантность (добавление константы к убыткам не влияет на оценку риска). Соблюдение этих аксиом позволяет использовать когерентные меры риска в качестве более надежной основы для принятия решений, связанных с риском, и для построения более эффективных систем управления капиталом, поскольку они предотвращают ситуации, когда диверсификация может привести к увеличению общего риска.

Для эффективной реализации когерентных мер риска, таких как Expected Shortfall (ES), критически важна оценка распределения убытков, осуществляемая с помощью продвинутых методов моделирования. Историческое моделирование (Historical Simulation) использует фактические исторические данные для построения эмпирического распределения убытков, что позволяет учесть нелинейности и ненормальность. Метод Монте-Карло (Monte Carlo Simulation) генерирует большое количество сценариев, основанных на заданных параметрах и зависимостях между факторами риска, позволяя получить статистическую оценку распределения убытков. Точность оценки напрямую зависит от количества симуляций и адекватности модели, используемой для описания взаимосвязей между факторами риска, например, многомерной гауссовской копулы.

Методы Монте-Карло часто используют многомерную Гауссову копулу для моделирования сложных зависимостей между факторами риска. Копула позволяет отделить моделирование маргинальных распределений отдельных факторов от моделирования их совместного распределения и корреляций. Многомерная Гауссова копула, в частности, предполагает, что совместное распределение факторов риска может быть описано с помощью Гауссова процесса, где корреляционная матрица определяет силу и направление взаимосвязей. Это позволяет генерировать сценарии, отражающие сложные зависимости, и оценивать распределение убытков в условиях стрессовых ситуаций, учитывая не только индивидуальные риски, но и их взаимодействие. Параметры копулы, такие как матрица корреляции, калибруются на основе исторических данных или экспертных оценок для адекватного представления взаимосвязей между факторами риска.

Анализ устойчивости кривой дефицита (DRC) в области 99,9% VaR демонстрирует, что даже незначительные изменения вероятностей дефолта, корреляций или объемов могут сместить DRC, не оказывая существенного влияния на величину потерь, что подчеркивает высокую чувствительность кривой к локальным флуктуациям в экстремальной области.

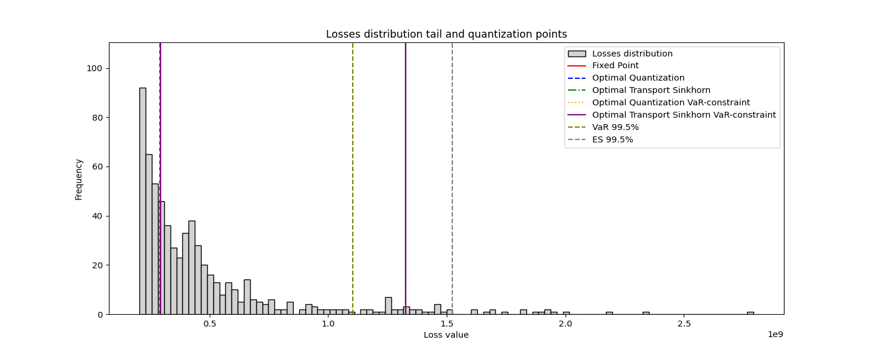
Уточнение оценки рисков: квантование и трёхточечные распределения

Квантование представляет собой метод аппроксимации непрерывных распределений вероятностей дискретными множествами, что существенно снижает вычислительную сложность при анализе рисков. Вместо работы с бесконечным числом возможных значений, квантование позволяет оперировать лишь ограниченным набором дискретных точек, представляющих исходное распределение. Такие методы, как оптимальный транспорт (Optimal Transport), позволяют минимизировать погрешность при переходе от непрерывного к дискретному представлению, находя оптимальное соответствие между точками исходного и дискретизированного распределения. Использование квантования особенно актуально в задачах, требующих высокой скорости вычислений, например, при моделировании портфелей или оценке кредитных рисков, где точное представление распределения потерь может быть ресурсоемким.

Трёхточечное распределение представляет собой упрощённую, но эффективную модель распределения убытков, основанную на трёх ключевых точках: нулевом убытке ($m_0$), умеренном убытке ($m_1$) и экстремальном убытке ($m_2$). Этот подход позволяет описать распределение убытков, выделяя наиболее вероятный сценарий (отсутствие убытков), типичный сценарий умеренных убытков и редкий, но критически важный сценарий экстремальных убытков. В отличие от более сложных моделей, трёхточечное распределение требует минимального количества параметров для определения, что упрощает расчеты и анализ рисков, при этом сохраняя достаточную точность для практических целей. Значение $m_2$ (экстремальный убыток) должно быть не меньше величины Value at Risk (VaR), что обеспечивает адекватную оценку максимальных потенциальных потерь.

Использование трёхточечного распределения напрямую интегрируется в подход величины и склонности (Magnitude-Propensity Approach), позволяя упростить расчет риска. В рамках данного подхода, вероятность наступления различных сценариев потерь, определенных в трёхточечном распределении (нулевые потери, умеренные потери и экстремальные потери), комбинируется с оценкой величины этих потерь. Это позволяет получить взвешенную оценку риска, которая является более вычислительно эффективной по сравнению с традиционными методами, требующими моделирования всей функции распределения потерь. В частности, $E[Loss] = m_0 p_0 + m_1 p_1 + m_2 * p_2$, где $m_i$ — величина потерь в сценарии $i$, а $p_i$ — вероятность наступления данного сценария. Таким образом, трёхточечное распределение служит основой для быстрого и точного вычисления ожидаемых потерь и оценки риска.

Трёхточечное распределение позволяет выявить несоответствия в традиционных методах оценки риска, таких как VaR (Value at Risk) и ES (Expected Shortfall). В частности, при использовании трёхточечного распределения, величина экстремальных потерь ($m_2$), представляющая собой один из параметров распределения, гарантированно должна быть не меньше значения VaR. Это связано с тем, что трёхточечное распределение явно моделирует сценарий наихудших потерь, в то время как VaR и ES могут недооценивать вероятность и величину таких событий, особенно при ненормальном характере распределения потерь. Таким образом, сравнение $m_2$ и VaR служит индикатором адекватности используемых методов оценки риска и позволяет выявить потенциальные недостатки в их реализации.

Аналитические основания: B-производные и H-функция

Вычисление производных, являющееся краеугольным камнем управления рисками, может быть осуществлено посредством B-производных, использующих специфическую функцию, обозначенную как H. Данный подход предоставляет альтернативный, но эквивалентный способ определения чувствительности финансовых инструментов к изменениям рыночных факторов. Функция H играет роль ключевого элемента в построении B-производной, позволяя описывать изменения цен активов в контексте более широкой модели рыночного поведения. В отличие от классических производных, B-производные обладают рядом преимуществ при работе с недифференцируемыми функциями и сложными финансовыми инструментами, обеспечивая более точную и надежную оценку рисков, особенно в условиях высокой волатильности и нелинейных взаимосвязей. Использование B-производных в сочетании с функцией H позволяет строить более устойчивые модели для анализа рисков и принятия обоснованных инвестиционных решений, что особенно важно для портфельных управляющих и финансовых аналитиков.

Установление B-дифференцируемости является фундаментальным требованием для обеспечения надежности и устойчивости расчетов в рамках данной аналитической модели. В то время как классические понятия дифференцируемости могут оказаться недостаточными для работы со сложными финансовыми инструментами и портфелями, B-дифференцируемость предоставляет более широкий и гибкий подход. Это позволяет корректно оценивать изменения в стоимости активов и рисков даже в условиях негладких или разрывных функций, что особенно важно при моделировании рыночных сценариев. Гарантируя существование B-производных, исследователи подтверждают, что алгоритмы расчета рисков будут давать стабильные и предсказуемые результаты, минимизируя вероятность ошибок и неточностей, которые могут привести к значительным финансовым потерям. Таким образом, B-дифференцируемость служит ключевым элементом в построении надежной и точной системы управления рисками.

Предложенный аналитический аппарат закладывает прочную основу для точной оценки и управления рисками в сложных инвестиционных портфелях. В его основе лежит возможность последовательного анализа взаимосвязей между различными активами, позволяя выявлять и количественно оценивать потенциальные потери даже в условиях высокой неопределенности. Данный подход, в отличие от упрощенных моделей, учитывает нелинейные зависимости и позволяет моделировать широкий спектр рыночных сценариев. Использование $B$-производных и $H$-функции обеспечивает математическую строгость и позволяет строить надежные прогнозы, что особенно важно для институциональных инвесторов и управляющих активами, стремящихся к оптимизации риско-доходности своих портфелей и соблюдению регуляторных требований.

В рамках разработанного аналитического подхода, оценка риска дефолта, выраженная в виде 1-летнего VaR (Value at Risk), успешно реализуется посредством метода Монте-Карло. Численные процедуры, используемые в симуляциях, демонстрируют сходимость к стабильным результатам, что подтверждает надежность и точность расчетов. Полученные данные свидетельствуют о высокой вычислительной эффективности алгоритмов, позволяя оперативно оценивать потенциальные убытки от дефолта в сложных инвестиционных портфелях. Такой подход обеспечивает возможность точного определения величины риска и способствует принятию обоснованных решений в области управления активами и пассивами, минимизируя потенциальные финансовые потери.

Согласование оценки рисков со стратегией организации

Эффективное управление рисками не сводится исключительно к технической точности расчетов и моделей. Ключевым фактором является согласование процессов оценки рисков с уровнем риска, который организация готова принять — её риск-аппетитом, и пределом отклонений от этого уровня — риск-толерантностью. Если оценка рисков не учитывает стратегические цели и готовность организации к потенциальным потерям, даже самые совершенные расчеты могут оказаться бесполезными или даже контрпродуктивными. Организация, стремящаяся к инновациям и росту, может быть готова принять более высокий уровень риска, чем консервативная компания, ориентированная на стабильность. Поэтому, понимание и интеграция этих организационных факторов в процесс управления рисками является необходимым условием для достижения долгосрочного успеха и устойчивости.

Рассмотрение взаимосвязи между частотой и серьёзностью рисков представляет собой ключевой инструмент в управлении рисками. Данный подход, известный как Частотно-Серьёзный анализ, позволяет организациям количественно оценить потенциальное воздействие различных рисков. Вместо того чтобы рассматривать каждый риск изолированно, он учитывает вероятность его возникновения (частоту) и потенциальный ущерб (серьёзность). Риски с высокой частотой и высокой серьёзностью требуют немедленного внимания, в то время как риски с низкой частотой и низкой серьёзностью могут быть приняты или отложены. Комбинируя эти два параметра, организации могут более эффективно приоритизировать свои усилия по смягчению рисков и распределять ресурсы, обеспечивая оптимальный баланс между стоимостью контроля и потенциальными потерями. Такой подход позволяет не только количественно оценить риски, но и наглядно продемонстрировать заинтересованным сторонам профиль риска организации и обосновать принятые решения.

Эффективная программа управления рисками формируется посредством интеграции передовых аналитических методов с чётким пониманием предпочтений организации. Использование сложных статистических моделей, таких как факторный анализ и сценарное планирование, позволяет выявлять и количественно оценивать потенциальные риски, однако, лишь сопоставление этих данных с установленным уровнем риска, который организация готова принять, обеспечивает реальную ценность. Успех в управлении рисками заключается не только в точности расчетов, но и в способности адаптировать стратегии к конкретным целям и культуре организации, позволяя принимать обоснованные решения и эффективно распределять ресурсы для минимизации негативных последствий и достижения устойчивого развития.

Перспективные исследования в области управления рисками должны быть направлены на интеграцию передовых методик с постоянно меняющимися нормативными требованиями и усложняющимися финансовыми инструментами. По мере развития финансовых рынков и появления новых видов активов, традиционные подходы к оценке рисков становятся недостаточно эффективными. Необходима разработка и внедрение более сложных моделей, учитывающих нелинейные зависимости и системные риски, а также адаптирующихся к изменениям в законодательстве и регуляторных стандартах. Особое внимание следует уделить разработке алгоритмов машинного обучения и искусственного интеллекта, способных автоматически выявлять и оценивать риски, связанные с новыми финансовыми инструментами и рыночными условиями, обеспечивая тем самым устойчивость и надежность финансовой системы.

Исследование, представленное в статье, подчеркивает важность перехода от скалярных мер риска, таких как VaR и ES, к более детализированной оценке, основанной на частоте и серьезности убытков. Этот подход позволяет учитывать не только величину потенциальных потерь, но и вероятность их наступления, что особенно важно для оценки рисков, связанных с производными финансовыми инструментами. Как заметил Ральф Уолдо Эмерсон: «Каждая машина, которую вы построили, является зеркалом вашей души». Подобно тому, как сложность души отражается в многообразии ее проявлений, так и сложность финансовых рисков требует отхода от упрощенных моделей в пользу более тонких и всеобъемлющих методов анализа. Предлагаемая методика, основанная на трехточечном распределении (нулевые, умеренные и экстремальные убытки), представляет собой шаг в этом направлении, позволяя банкам лучше понимать и управлять своими рисками.

Что дальше?

Предложенный подход, расширяющий рамки оценки частоты и серьезности потерь до трехточечного распределения, не столько предлагает новый инструмент контроля, сколько обнажает иллюзорность самого понятия «контроль» в системах, подверженных случайным воздействиям. Устойчивость, как показывает практика, возникает не из централизованного управления, а из локальных правил, формирующихся на уровне взаимодействий. Использование оптимального транспорта и квантования, безусловно, повышает точность описания рисковых сценариев, однако истинная ценность заключается в возможности более адекватного восприятия неопределенности, а не в попытках ее подавления.

Очевидным направлением дальнейших исследований представляется изучение возможности применения данного подхода к более сложным производным финансовым инструментам, особенно учитывая растущую роль B-деривативов. Однако, более фундаментальным вопросом остается разработка методов адаптации данной системы к изменяющимся условиям рынка. Попытки создать универсальный инструмент измерения риска обречены на провал; гораздо перспективнее создание гибких, самоорганизующихся систем, способных учитывать локальные особенности и быстро адаптироваться к новым вызовам.

В конечном итоге, предложенный подход, подобно многим другим инновациям в области управления рисками, является лишь инструментом. Его эффективность зависит не от математической точности, а от способности признать, что порядок не нуждается в архитекторе — он возникает из локальных правил. Влияние, а не контроль, — вот истинный путь к устойчивости.

Оригинал статьи: https://arxiv.org/pdf/2511.21556.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-11-28 04:17