Нейросети на службе прочности материалов: новый подход к решению сложных задач

Автор: Денис Аветисян

Исследователи предложили инновационный метод решения уравнений линейной упругости, объединяющий возможности графовых нейронных сетей и частотного анализа.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

На рисунке демонстрируется анализ производительности алгоритма AG-FNS на неструктурированной сетке Data-1, показывающий траекторию обучения, его поведение в качестве итерационного решателя и его эффективность в роли предварительного решателя для FGMRES.

Разработанный многоуровневый адаптивный графовый Фурье-нейронный решатель (ML-AG-FNS) демонстрирует превосходство над традиционными методами при решении крупномасштабных задач на неструктурированных сетках.

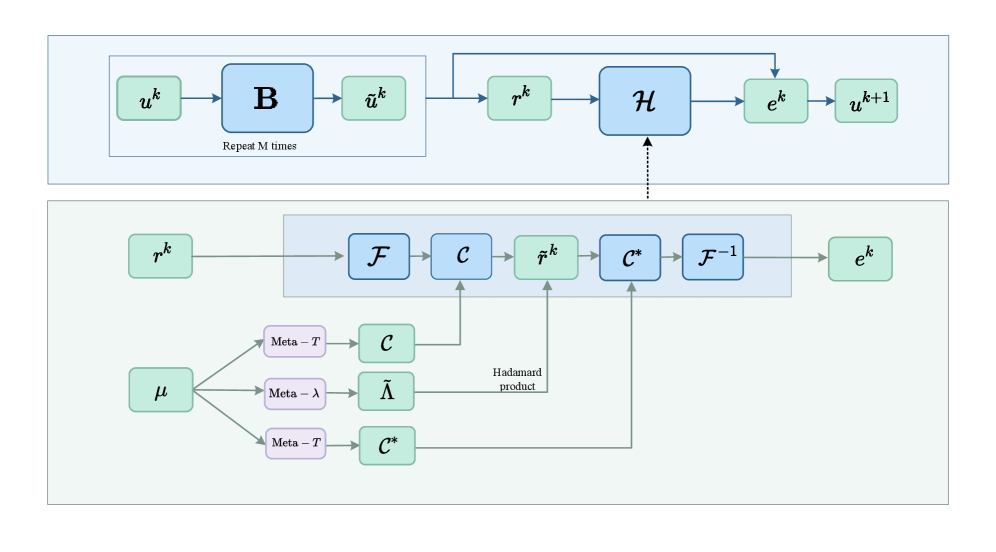
Численное решение уравнений линейной упругости на неструктурированных сетках представляет собой сложную задачу, особенно при наличии неоднородных и анизотропных материалов. В данной работе, посвященной ‘Vertex-based Graph Neural Solver and its Application to Linear Elasticity Equations’, предложен новый итеративный решатель, объединяющий преимущества сглаживания Блока-Якоби с обучаемым нейронным корректором в частотной области. Предложенный подход демонстрирует превосходную устойчивость и эффективность по сравнению с классическим методом мультисеточной агрегации, обеспечивая значительное ускорение сходимости. Каковы перспективы дальнейшего развития гибридных методов, сочетающих традиционные численные подходы с возможностями нейронных сетей для решения задач механики сплошных сред?

Вызов Масштаба в Численном Моделировании

Традиционные итерационные методы играют ключевую роль в решении масштабных разреженных систем линейных уравнений, которые являются основой метода конечных элементов. Данные методы, такие как метод сопряженных градиентов или GMRES, позволяют численно моделировать поведение сложных систем, разбивая задачу на множество мелких, связанных между собой уравнений. Эффективность этих методов заключается в их способности использовать разреженность системы — то есть, большое количество нулевых элементов в матрице коэффициентов — для снижения вычислительных затрат и требований к памяти. Именно благодаря этим свойствам итерационные методы стали незаменимым инструментом в различных областях, включая структурный анализ, гидродинамику и электромагнитное моделирование, позволяя инженерам и ученым предсказывать поведение сложных материалов и конструкций с высокой точностью.

Традиционные итеративные методы, являющиеся основой для решения масштабных разреженных систем линейных уравнений, необходимых в конечноэлементном моделировании, всё чаще сталкиваются с трудностями при работе с возрастающей сложностью и масштабом современных симуляций. Это связано с тем, что требуемые вычислительные ресурсы растут непропорционально увеличению размера модели и детализации решаемой задачи. Решение сложных задач, особенно связанных с моделированием материалов с анизотропными свойствами, может потребовать огромных объемов памяти и времени процессора, что ограничивает возможности исследователей и инженеров. Поиск оптимальных алгоритмов и аппаратных решений для преодоления этих ограничений является ключевой задачей в области численного моделирования.

Эффективность итеративных методов решения больших разреженных систем линейных уравнений, критически важных для моделирования методом конечных элементов, в значительной степени зависит от качества исходного приближения. Получение точного и эффективного начального решения представляет собой сложную задачу, требующую значительных вычислительных ресурсов. Неудачный выбор начального приближения может привести к замедлению сходимости, увеличению числа итераций и, как следствие, к существенному увеличению времени вычислений. Более того, процесс получения хорошего начального приближения сам по себе может быть вычислительно затратным, нивелируя преимущества использования итеративных методов. Поэтому разработка эффективных и экономичных стратегий для получения качественного исходного решения является ключевой задачей в области численного моделирования.

При моделировании сложных материалов, таких как анизотропные среды, применение линейной модели упругости требует значительно больших вычислительных ресурсов. Это связано с тем, что анизотропия подразумевает зависимость механических свойств от направления, что приводит к более сложной и объёмной системе уравнений. В отличие от изотропных материалов, где достаточно описать упругие характеристики всего двумя параметрами (модуль Юнга и коэффициент Пуассона), анизотропные материалы требуют описания через тензор упругих свойств — матрицу $C_{ijkl}$ — содержащую большее число независимых параметров. Решение системы уравнений, основанных на таком тензоре, требует больше памяти и вычислительной мощности, особенно при использовании численных методов, таких как метод конечных элементов. Увеличение числа параметров и сложность тензора упругих свойств напрямую влияют на время решения и требуемые ресурсы, что становится критичным фактором при моделировании крупномасштабных структур и процессов.

Сравнение различных итерационных решателей и предварительных решателей для FGMRES на задаче Data-3 (2D анизотропия) демонстрирует их влияние на скорость сходимости.

Нейронные Решатели: Новый Подход к Численным Методам

Нейронные решатели представляют собой новый подход к численным методам, объединяющий глубокое обучение с традиционными итерационными алгоритмами. Данный подход направлен на преодоление ограничений, связанных со скоростью и эффективностью классических методов, особенно при решении сложных задач, требующих значительных вычислительных ресурсов. В отличие от традиционных алгоритмов, которые полагаются на заранее определенные правила и структуры, нейронные решатели используют возможности глубоких нейронных сетей для обучения отображению между параметрами задачи и полями решений. Это позволяет им адаптироваться к конкретным проблемам и оптимизировать процесс вычислений, что потенциально приводит к значительному ускорению сходимости и повышению общей эффективности решения $f(x) = 0$.

Методы нейронных решателей используют возможности глубокого обучения для установления соответствия между параметрами задачи и полями решений. Этот подход позволяет модели научиться аппроксимировать функцию, отображающую входные параметры в выходное решение, минуя традиционные итеративные вычисления. Вместо последовательного приближения к решению, нейронная сеть, обученная на наборе данных, может напрямую предсказывать решение для новых параметров, что потенциально обеспечивает значительное ускорение процесса вычислений, особенно для задач, требующих многократного решения с разными входными данными. Обучение сети осуществляется на основе данных, полученных от традиционных численных методов или экспериментальных данных, что позволяет нейронной сети улавливать сложные зависимости и находить оптимальные решения.

Методы взвешенных итераций Якоби и итераций Чебышева могут быть значительно улучшены за счет использования нейронных сетей для обучения оптимальным предварителям и весам итераций. Традиционно, выбор предварителей и весов требует экспертных знаний и часто является эмпирическим процессом. Нейронные сети, обученные на данных, полученных в результате решения большого числа задач, способны выявлять сложные зависимости и определять оптимальные параметры, минимизирующие число итераций, необходимых для достижения заданной точности. Это позволяет адаптировать алгоритм к конкретным задачам и значительно ускорить сходимость по сравнению с использованием фиксированных или заранее заданных параметров. Обученные нейронные сети, выступая в роли нелинейных функций, эффективно аппроксимируют обратную матрицу системы, что повышает устойчивость и эффективность итерационного процесса, особенно для плохо обусловленных задач, где стандартные методы могут демонстрировать медленную сходимость или расходиться.

Основная идея нейронных решателей заключается в переходе от традиционных алгоритмов численного решения к подходам, основанным на данных. Вместо жестко заданных итерационных процедур, эти методы используют глубокое обучение для аппроксимации отображения между параметрами задачи и полями решений. Это позволяет обучать модели, которые непосредственно предсказывают решения, либо оптимизировать параметры существующих итерационных алгоритмов, таких как методы Якоби или Чебышева, с целью ускорения сходимости и повышения эффективности. Такой подход позволяет использовать накопленные данные для адаптации алгоритма к конкретной задаче, что потенциально приводит к значительному улучшению производительности по сравнению со статическими, универсальными алгоритмами.

Гибридный итерационный алгоритм G-FNS использует нейронную сеть, динамически генерирующую матрицы перехода и фильтры на основе параметров задачи, для итеративного уточнения решения путем обработки остаточной ошибки в частотной области.

Глубокие Операторы: Изучение Пространства Решений

Нейронные операторы, такие как DeepONet, расширяют возможности нейронных решателей, изучая полное отображение из функционального пространства в функциональное пространство. В отличие от традиционных подходов, оперирующих дискретизированными данными, нейронные операторы напрямую моделируют связь между функциями. Это достигается за счет архитектуры, способной принимать на вход функции и выдавать на выходе другие функции, без необходимости явного определения дискретной сетки или конечных элементов. Фактически, нейронный оператор аппроксимирует оператор, действующий на функции, позволяя решать задачи, определяемые функциональными уравнениями, такие как $u(x) = \int K(x,y)f(y)dy$, без дискретизации области определения функций $u$ и $f$. Такой подход обеспечивает более гибкое и потенциально более точное решение, особенно в задачах, где дискретизация затруднена или требует больших вычислительных затрат.

Традиционные численные методы решения частных дифференциальных уравнений (ПДУ) требуют явной дискретизации области определения задачи, что подразумевает разбиение непрерывной области на конечное число элементов и аппроксимацию решения в каждой точке этой дискретизации. В отличие от этого, нейронные операторы позволяют решать ПДУ без предварительной дискретизации, напрямую отображая функции из одного функционального пространства в другое. Это обеспечивает большую гибкость при работе с задачами, имеющими сложную геометрию или требующими адаптивной точности, а также потенциально повышает точность решения за счет избежания ошибок дискретизации, возникающих при использовании конечных разностей или конечных элементов. Вместо аппроксимации решения на дискретной сетке, нейронный оператор учится представлять решение как функцию непрерывной переменной, что особенно полезно для задач, где точное решение неизвестно или вычислительно затратно.

Сети, обученные с учетом физических принципов (Physics-Informed Neural Networks, PINN), улучшают подход к решению задач за счет включения управляющих уравнений непосредственно в функцию потерь. Это достигается путем добавления к стандартной функции потерь членов, представляющих остаток уравнений в частных производных (например, $ \nabla^2 u + f(x,y) = 0 $). В результате, при обучении сети, минимизация функции потерь одновременно оптимизирует соответствие решения данным и удовлетворяет физическим законам, что повышает достоверность и точность полученных результатов, особенно в случаях ограниченного количества данных или при экстраполяции за пределы обучающей выборки.

Архитектуры глубоких операторов, такие как DeepONet, находят применение в широком спектре вычислительных задач. Они успешно применяются для решения как простых линейных систем уравнений, например, $Ax = b$, так и сложных нелинейных симуляций, включающих нелинейные частные дифференциальные уравнения (ЧДУ). Возможность работы с функциями, а не дискретными данными, позволяет эффективно моделировать задачи, где традиционные численные методы требуют значительных вычислительных ресурсов или сталкиваются с проблемами сходимости. Примеры включают моделирование турбулентности, динамику жидкостей, а также задачи обратной задачи, где необходимо восстановить параметры системы по наблюдаемым данным.

Адаптивный оператор в AG-FNS использует обучаемую сеть для преобразования физических координат в латентные, что позволяет динамически формировать базисные функции в преобразовании Фурье и эффективно решать задачи с переменными коэффициентами.

Повышение Эффективности с Декомпозицией Области

Сочетание нейронных решателей с проверенными методами, такими как декомпозиция области, позволяет значительно повысить производительность и масштабируемость при решении сложных вычислительных задач. Данный подход использует преимущества обоих типов методов: нейронные сети эффективно аппроксимируют локальные решения, а декомпозиция области разбивает большую проблему на более мелкие, решаемые параллельно подзадачи. Это не только ускоряет процесс вычислений, но и позволяет решать задачи, которые были бы недоступны для традиционных методов из-за ограничений по памяти или вычислительной мощности. Результаты показывают, что гибридные системы, объединяющие нейронные сети и декомпозицию области, превосходят классические алгоритмы, особенно при моделировании анизотропных материалов и решении задач с большим количеством степеней свободы, достигающих, например, 11,055.

Метод доменного разложения предполагает разделение сложной задачи на ряд более простых, независимых подзадач. Такой подход позволяет решать каждую из них параллельно, существенно сокращая общее время вычислений и повышая эффективность решения. Разделение происходит путем разбиения исходной области на отдельные домены, каждый из которых обрабатывается независимо. Впоследствии, результаты, полученные для каждого домена, объединяются для формирования полного решения исходной задачи. Эффективность этого метода возрастает с увеличением числа доступных вычислительных ресурсов, позволяя масштабировать решение для задач, требующих значительных вычислительных мощностей и больших объемов данных, например, при моделировании сложных физических процессов или решении крупномасштабных инженерных задач.

Эффективность метода доменного разложения напрямую зависит от корректно заданных граничных условий на интерфейсах между поддоменами. Эти условия, известные как условия передачи, обеспечивают согласованность решений в соседних областях, предотвращая появление искусственных разрывов и гарантируя сходимость итерационного процесса. Неправильно сформулированные условия передачи могут приводить к возникновению ошибок, замедлению сходимости или даже к расходимости алгоритма. Поэтому, разработка и выбор оптимальных условий передачи является ключевым аспектом при реализации доменного разложения для решения сложных вычислительных задач, особенно в контексте неоднородных материалов и геометрий, где требуется высокая точность и эффективность численного моделирования. Примером может служить использование условий Неймана или Дирихле, выбор которых определяется физической природой решаемой задачи и свойствами моделируемой среды.

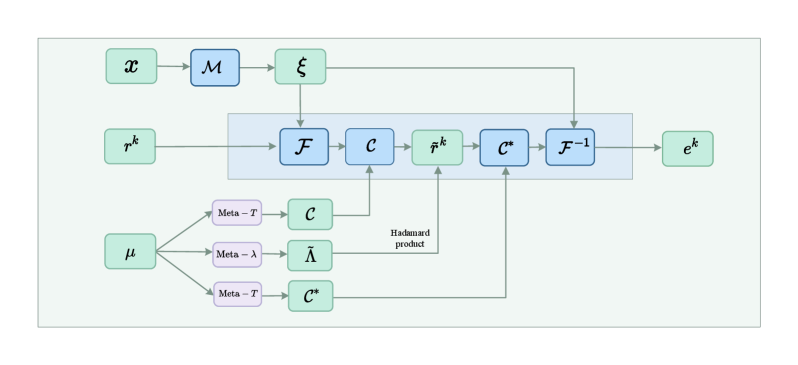
Представленный подход объединяет преимущества традиционных численных методов и возможностей машинного обучения, предлагая эффективное решение для сложных симуляций. Разработанный Multilevel Adaptive Graph Fourier Neural Solver (ML-AG-FNS) демонстрирует превосходство над методами Smoothed Aggregation Algebraic Multigrid (SA-AMG), особенно при моделировании анизотропных материалов. Проведенные исследования показывают, что ML-AG-FNS обеспечивает более высокую производительность при решении задач до 11,055 степеней свободы, что открывает перспективы для масштабирования и применения в широком спектре научных и инженерных областей, где требуются высокоточные и быстрые вычисления.

Сравнение алгоритмов AG-FNS и ML-AG-FNS на данных Data-2 показывает, что ML-AG-FNS превосходит AG-FNS как в скорости сходимости, так и в качестве решения, выступая в роли итерационного решателя и предварительного обусловливателя для FGMRES.

Представленная работа демонстрирует стремление к математической чистоте в решении сложных задач линейной упругости. Разработанный метод, объединяющий графовые нейронные сети и частотный анализ, представляет собой элегантное решение, где каждая операция в многоуровневом адаптивном графовом преобразовании Фурье (ML-AG-FNS) имеет четкое обоснование. Как заметил Эрвин Шрёдингер: «Вся материя является волной, а волна — материей». Эта фраза, хотя и относится к квантовой механике, перекликается с подходом, представленным в статье: преобразуя проблему в частотную область и используя волновую природу графовых сигналов, авторы достигают высокой эффективности и точности, подобно тому, как Шрёдингер описал взаимосвязь между материей и волнами. Доказательство корректности алгоритма, а не просто его работа на тестовых примерах, является ключевым аспектом этой работы, соответствующим философии истинной элегантности кода.

Что Дальше?

Без строгого определения задачи, любое решение — лишь шум, маскирующийся под порядок. Представленная работа демонстрирует потенциал гибридных итерационных методов, опирающихся на графовые нейронные сети, в решении задач линейной упругости. Однако, эвристическая природа обучения нейронных сетей накладывает ограничения на формальную доказуемость сходимости. Дальнейшие исследования должны быть направлены на интеграцию принципов математической строгости в архитектуру нейронных решателей.

Особое внимание следует уделить анализу спектральных свойств операторов, возникающих в задачах упругости, и разработке прекондиционирователей, адаптированных к особенностям этих спектров. Необходимо исследовать возможность построения нейронных сетей, способных автоматически выявлять и использовать структуру оператора для ускорения сходимости и повышения устойчивости. Игнорирование фундаментальных ограничений, накладываемых теорией, неминуемо ведет к появлению решений, корректных лишь на конечном подмножестве тестовых случаев.

В конечном счете, истинная элегантность решения проявляется не в скорости вычислений, а в его математической чистоте. Разработка алгоритмов, которые можно доказать, а не просто протестировать, — вот истинная цель, к которой следует стремиться. Иначе все усилия рискуют превратиться в создание сложных инструментов для решения неверных задач.

Оригинал статьи: https://arxiv.org/pdf/2511.21491.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-11-29 22:18