Спектры сильных корреляций: новый подход к моделированию материалов

Автор: Денис Аветисян

В статье представлена эффективная методика расчета спектральных функций в сильно коррелированных материалах, объединяющая возможности комплексного времени и тензорных сетей.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Функции спектральной плотности, вычисленные методом DMFT для одноорбитальной модели при различных значениях [latex]U[/latex] и [latex]U/D = 2.4, 2.6[/latex] (с [latex]N_b = 179[/latex] и [latex]D t_{max} = 60[/latex]) и [latex]U/D = 3.3[/latex] (с [latex]N_b = 59[/latex] и [latex]D t_{max} = 30[/latex]), демонстрируют зависимость электронной структуры от взаимодействия и параметров симуляции, полученную посредством комплексных временных вычислений при [latex]\alpha = 0.2[/latex] и [latex]\chi = 60[/latex]. — Функции спектральной плотности, вычисленные методом DMFT для одноорбитальной модели при различных значениях $U$ и $U/D = 2.4, 2.6$ (с $N_b = 179$ и $D t_{max} = 60$ ) и $U/D = 3.3$ (с $N_b = 59$ и $D t_{max} = 30$ ), демонстрируют зависимость электронной структуры от взаимодействия и параметров симуляции, полученную посредством комплексных временных вычислений при $\alpha = 0.2$ и $\chi = 60$ .

Предложен метод, сочетающий комплексновременные тензорные решатели с аналитическим продолжением на основе ESPRIT для точного моделирования спектральных функций в рамках многоорбитальной теории динамического среднего поля.

Несмотря на значительный прогресс в теории функциональной интеграции, точное вычисление спектральных функций в сильно коррелированных материалах остается сложной задачей. В данной работе, посвященной ‘Multi-orbital dynamical mean-field theory with a complex-time solver’, предложен новый подход, сочетающий комплексновременные тензорные сети с аналитическим продолжением, основанным на экспоненциальной аппроксимации. Разработанный метод позволяет эффективно и точно восстанавливать спектральные характеристики, снижая вычислительные затраты по сравнению с традиционными методами, основанными на реальном или мнимом времени. Открывает ли предложенный подход новые горизонты для ab initio исследований материалов с сильными электронными корреляциями и позволит ли он лучше понять их физические свойства?

Понимание Коррелированных Систем: Вызов для Новых Методов

Понимание систем с сильной электронной корреляцией имеет первостепенное значение для открытия новых материалов с уникальными свойствами, однако традиционные методы, основанные на независимом приближении электронов, оказываются недостаточно эффективными для их адекватного описания. В этих системах взаимодействие между электронами настолько велико, что оно кардинально изменяет их поведение, приводя к возникновению экзотических состояний материи, таких как высокотемпературная сверхпроводимость или магнетизм с необычными характеристиками. Стандартные подходы, успешно работающие для простых металлов, не способны учесть сложные коллективные эффекты, возникающие в сильно коррелированных системах, что требует разработки принципиально новых теоретических и вычислительных методов для предсказания и понимания их свойств. Именно поэтому, прогресс в этой области напрямую связан с поиском инновационных подходов к решению многочастичной задачи, учитывающих взаимодействие между электронами на всех масштабах.

В сильно коррелированных системах взаимодействие между электронами настолько значительно, что описание поведения каждого электрона по отдельности, как в традиционных подходах, становится принципиально неверным. Электроны в таких системах формируют коллективные состояния, где их поведение определяется не индивидуальными свойствами, а взаимовлиянием друг с другом. Поэтому для адекватного понимания и предсказания свойств этих материалов необходимо использовать методы, учитывающие взаимодействие многих частиц — так называемый многочастичный подход. Такие методы позволяют выйти за рамки упрощенных моделей и описывать сложные явления, такие как сверхпроводимость, магнетизм и другие экзотические состояния материи, которые не могут быть объяснены в рамках одночастичной картины. $Ψ(r_1, ..., r_N)$ — волновая функция, описывающая все электроны в системе, является ключевым элементом этих расчетов и требует значительных вычислительных ресурсов.

Теория Динамического Среднего Поля: Мост Между Теоретическими Расчетами и Реальностью

Теория динамического среднего поля (DMFT) позволяет свести многочастичную задачу о взаимодействии электронов в кристаллической решетке к эффективной модели примеси. В рамках DMFT, взаимодействия между электронами в решетке заменяются самосогласованным средним полем, которое действует на каждый электрон. Это преобразование, по сути, заменяет сложную задачу с бесконечным числом взаимодействующих частиц на задачу, описывающую поведение одного электрона, движущегося в эффективном поле, включающем эффекты всех остальных электронов. Математически, это достигается путем введения $G(k, \omega)$ — функции Грина, которая описывает эволюцию электрона с волновым вектором $k$ и энергией ω в этом эффективном поле. Решение для этой функции Грина позволяет получить информацию о свойствах системы, таких как спектральная функция и плотность состояний.

Решение полученной эффективной модели примеси является вычислительно наиболее сложной задачей в рамках теории динамического среднего поля (DMFT). Традиционно, для этого используются итерационные схемы, такие как алгоритм самосогласованности, требующие последовательного решения одночастичного уравнения и обновления функции Грина. Вычислительная стоимость этих схем масштабируется как $O(N^3)$ или выше, где $N$ — размер матрицы, что ограничивает применимость метода к системам с большим числом атомов. Для повышения эффективности применяются различные оптимизации, включая использование разреженных матричных операций и предварительных решателей, однако, несмотря на это, решение модели примеси остается узким местом при проведении расчетов в рамках DMFT.

Многоорбитальные формулировки в рамках теории динамических средних полей (DMFT) являются критически важными для проведения реалистичных расчетов свойств материалов. В реальных материалах электроны не ограничены одной орбиталью, а распределены по нескольким $d$ или $f$ орбиталям. Учет этих орбитальных степеней свободы необходим для корректного описания электронных корреляций и, следовательно, электронных и магнитных свойств. Игнорирование многоорбитальности приводит к упрощенным моделям, не способным точно воспроизводить экспериментальные данные по сложным материалам, таким как оксиды переходных металлов и интерметаллиды. Расчеты в многоорбитальном приближении требуют значительно больших вычислительных ресурсов, но позволяют получить адекватное описание спектральных функций, магнитных моментов и других ключевых характеристик материалов.

Спектральные функции двухорбитальной модели Хаббарда при [latex]U=1.6D[/latex], [latex]J=0.25U[/latex] и различных уровнях допирования демонстрируют эволюцию структуры с изменением химического потенциала [latex]\mu/D[/latex], при этом результаты, полученные методами комплексного и реального времени с [latex]\chi=40[/latex], показывают хорошее соответствие. — Спектральные функции двухорбитальной модели Хаббарда при $U=1.6D$ , $J=0.25U$ и различных уровнях допирования демонстрируют эволюцию структуры с изменением химического потенциала $\mu/D$ , при этом результаты, полученные методами комплексного и реального времени с $\chi=40$ , показывают хорошее соответствие.

Комплексные Временные Методы: Раскрытие Потенциала Вычислительной Эффективности

Формулировка динамической теории среднего поля (DMFT) в комплексном времени обеспечивает более стабильное и эффективное решение модели примеси. Традиционные методы решения модели примеси в реальном времени часто сталкиваются с проблемами численной нестабильности и требуют больших вычислительных ресурсов. Переход к комплексной временной области позволяет избежать этих проблем, используя свойства аналитического продолжения и обеспечивая сходимость численных процедур. Этот подход позволяет получить более точные результаты за меньшее время, особенно в задачах, требующих вычисления спектральных функций и других частотно-зависимых величин. В частности, использование комплексного времени упрощает процедуру самосогласования в DMFT и позволяет эффективно решать задачи с сильными электронными корреляциями.

Комплексно-временной тензорный решатель примесных задач использует квантовую запутанность для представления функции Грина примеси, что позволяет значительно повысить вычислительную мощность. В отличие от методов, работающих в реальном времени, данный подход обеспечивает существенное сокращение времени моделирования. Представление функции Грина примеси в виде тензорной сети позволяет эффективно описывать корреляции между степенями свободы примеси, используя ограниченные вычислительные ресурсы. Эффективность достигается за счет компактного представления волновой функции примеси, что особенно важно для задач с сильными электронными корреляциями, где традиционные методы становятся вычислительно затратными.

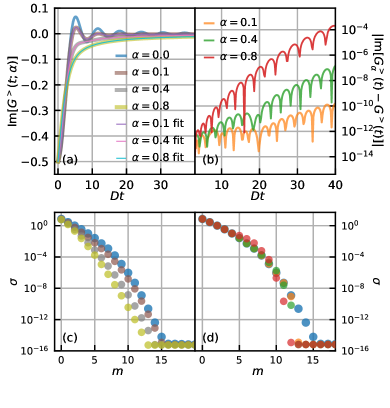
Комплекновременная функция Грина выступает ключевым промежуточным звеном при вычислении свойств в реальном времени. Методика позволяет получать результаты, сопоставимые по точности с высокоточными расчетами в реальном времени, достигнутыми при использовании размерности связей $\chi=1500$ . Это достигается за счет эффективного представления корреляционных функций в комплексной плоскости времени, что упрощает вычисление динамических свойств системы и снижает вычислительные затраты по сравнению с прямыми расчетами в реальном времени.

Анализ функции Грина, выполненный вдоль комплексных временных контуров с различными углами α, показывает, что ошибка реконструкции функции Грина во времени обратно пропорциональна спектру сингулярных чисел матрицы Ханкеля.

От Теории к Наблюдению: Влияние на Реальные Свойства Материалов

Спектральная функция, получаемая в рамках расчетов по методу динамической теории среднего поля (DMFT), представляет собой ключевой инструмент для понимания энергетического распределения электронов в материале. Она описывает вероятность нахождения электрона с определенной энергией в системе, что позволяет напрямую сравнивать теоретические предсказания с экспериментальными данными, полученными, например, с помощью спектроскопии фотоэмиссии или спектроскопии потерь энергии электронов. По сути, эта функция выступает мостом между сложными теоретическими моделями и наблюдаемыми физическими свойствами, позволяя исследователям проверять адекватность используемых приближений и углублять понимание электронного строения материалов. $A(ω)$ — таким образом обозначается спектральная функция — содержит информацию о возбуждениях в системе и является фундаментальной характеристикой, определяющей ее оптические и транспортные свойства.

В последние годы методы динамической теории среднего поля в реальной частоте (DMFT) и ESPRIT стали незаменимыми инструментами для исследования электронных свойств материалов. В отличие от традиционных подходов, требующих аналитического продолжения, эти методы позволяют напрямую вычислять спектральные функции — графическое представление распределения энергии электронов в материале. Это значительно упрощает процесс анализа и повышает точность результатов, поскольку исключает потенциальные ошибки, связанные с процедурой аналитического продолжения. Полученные спектральные функции могут быть непосредственно сопоставлены с экспериментальными данными, полученными, например, с помощью спектроскопии, что позволяет проверить теоретические модели и получить глубокое понимание поведения электронов в сложных материалах. Такой подход открывает новые возможности для изучения коррелированных электронных систем и разработки материалов с заданными свойствами.

Для точного предсказания поведения материалов критически важно понимание взаимодействия различных электронных корреляций, таких как обменное взаимодействие Хунда и взаимодействие Канами. Взаимодействие Хунда, обусловленное спиновым выравниванием электронов, существенно влияет на магнитные свойства, а взаимодействие Канами, возникающее из-за кулоновского отталкивания между электронами, определяет особенности электронной структуры и спектральные характеристики. Спектральная функция, получаемая методами DMFT, позволяет непосредственно исследовать влияние этих взаимодействий на распределение энергии электронов, предоставляя возможность сопоставить теоретические предсказания с экспериментальными данными. Учет этих корреляций необходим для адекватного описания сложных электронных систем и прогнозирования их физических свойств, включая сверхпроводимость, магнетизм и оптические характеристики.

Спектральная функция, рассчитанная методом DMFT для трехорбитальной модели Хаббарда при [latex]D=1[/latex], [latex]U/D=4[/latex], [latex]J=0.15U[/latex] и [latex]\mu/D=-1.0[/latex] (что соответствует [latex]n\\approx1.0[/latex]), демонстрирует характерные особенности при параметрах симуляции [latex]\\alpha=0.2[/latex], [latex]N_b=239[/latex], [latex]t_{max}=60D[/latex] и [latex]\\chi=90[/latex]. — Спектральная функция, рассчитанная методом DMFT для трехорбитальной модели Хаббарда при $D=1$ , $U/D=4$ , $J=0.15U$ и $\mu/D=-1.0$ (что соответствует $n\\approx1.0$ ), демонстрирует характерные особенности при параметрах симуляции $\\alpha=0.2$ , $N_b=239$ , $t_{max}=60D$ и $\\chi=90$ .

За Пределами Современных Ограничений: Будущие Направления и Применение

Сочетание усовершенствованных решателей примесных задач с эффективными методами, работающими в реальной частотной области, открывает принципиально новые возможности для ускорения процесса открытия и проектирования материалов. Традиционно, моделирование электронных свойств материалов требовало значительных вычислительных ресурсов и упрощающих предположений. Однако, данная комбинация позволяет преодолеть эти ограничения, обеспечивая более точное и быстрое предсказание характеристик материалов, таких как проводимость, магнитные свойства и оптические отклики. Это особенно важно при исследовании сложных материалов, где корреляции между электронами играют решающую роль. Благодаря более эффективному учету этих корреляций, ученые смогут более целенаправленно синтезировать и изучать материалы с заданными свойствами, что приведет к прорывам в различных областях, включая электронику, энергетику и катализ. Разработка новых материалов станет возможна не только путем случайного поиска, но и на основе предсказаний, полученных с помощью этих передовых вычислительных методов.

Применение динамической теории среднего поля (DMFT) к сложным решеткам, в частности, к решетке Бете, открывает уникальные возможности для изучения фундаментальных моделей физики конденсированного состояния и понимания возникающих явлений. Решетка Бете, характеризующаяся координационным числом z, служит идеальной платформой для исследования влияния топологии решетки на электронные свойства материалов. Исследования показывают, что DMFT позволяет выявлять фазовые переходы, исследовать влияние корреляций между электронами и рассчитывать спектральные функции, что необходимо для интерпретации экспериментальных данных. Этот подход позволяет глубже понять механизмы возникновения экзотических состояний материи и предсказывать свойства новых материалов, обладающих необычными электронными и магнитными характеристиками. Использование DMFT для изучения сложных решеток способствует развитию теоретической базы для создания материалов с заданными свойствами и расширяет горизонты квантовых технологий.

Дальнейшее развитие предложенных методик открывает перспективы для исследования экзотических материалов, обладающих необычными свойствами, и продвижения в области квантовых технологий. Исследования демонстрируют стабильную сходимость алгоритмов даже при сложных углах до α=0.4, что позволяет моделировать более реалистичные системы. Однако необходимо учитывать, что погрешность в восстановлении ключевых количественных характеристик возрастает с увеличением значения α, что требует дальнейшей оптимизации подходов к повышению точности расчетов и расширению диапазона применимости методов к материалам с еще более сложной структурой и взаимодействиями. Подобные усовершенствования позволят не только лучше понимать фундаментальные свойства материи, но и создавать новые материалы с заданными характеристиками для применения в передовых технологиях.

Сравнение результатов симуляций DMFT в реальном (пунктир) и комплексном (сплошная линия) времени при [latex]U=2D[/latex], [latex]N_b=179[/latex] и [latex]D_t^{max}=60[/latex] показывает хорошее соответствие при [latex]\\mu/D=-1.00[/latex] ([latex]n=1[/latex], синяя линия, [latex]\\chi=30[/latex]) и [latex]\\mu/D=-0.25[/latex] ([latex]n\\approx0.72[/latex], оранжевая линия, [latex]\\chi=40[/latex]), при этом комплексные симуляции выполнялись с [latex]\\alpha=0.2[/latex]. — Сравнение результатов симуляций DMFT в реальном (пунктир) и комплексном (сплошная линия) времени при $U=2D$ , $N_b=179$ и $D_t^{max}=60$ показывает хорошее соответствие при $\\mu/D=-1.00$ ( $n=1$ , синяя линия, $\\chi=30$ ) и $\\mu/D=-0.25$ ( $n\\approx0.72$ , оранжевая линия, $\\chi=40$ ), при этом комплексные симуляции выполнялись с $\\alpha=0.2$ .

Исследование, представленное в данной работе, демонстрирует стремление к пониманию фундаментальных принципов, лежащих в основе сложных систем. Авторы, используя комбинацию методов динамической теории среднего поля и тензорных сетей, стремятся не просто вычислить спектральные функции, но и раскрыть скрытые взаимосвязи в сильно коррелированных материалах. В этом контексте, уместно вспомнить слова Конфуция: “Изучай прошлое, чтобы знать будущее”. Подобно тому, как понимание истории позволяет предвидеть тенденции, глубокий анализ теоретических моделей и вычислительных методов открывает путь к созданию новых материалов с заданными свойствами. Особое внимание к точному расчету самоэнергии, как ключевого элемента, подтверждает важность детального анализа и стремления к полному пониманию системы.

Что дальше?

Представленный подход, комбинирующий решатели на основе тензорных сетей во временной области с аналитическим продолжением, безусловно, открывает новые возможности для изучения спектральных функций в сильно коррелированных материалах. Однако, следует признать, что любое приближение — это лишь карта, а не территория. Эффективность метода, как и любого другого, сталкивается с ограничениями применимости к системам с ещё более сложной структурой и взаимодействиями. Вопрос о масштабируемости — вечная проблема вычислительной физики — остаётся открытым, требуя поиска новых алгоритмов и аппаратных решений.

Интересно, что, решая задачу вычисления спектральных функций, исследователи неизбежно сталкиваются с более фундаментальным вопросом: насколько точно мы вообще можем определить «истинный» спектр? Любое измерение, любая симуляция несут в себе погрешности и упрощения. Поэтому, дальнейшее развитие методов аналитического продолжения, возможно, должно быть направлено не только на повышение точности, но и на разработку способов оценки неопределённости и чувствительности результатов к различным параметрам.

В конечном счёте, успех этого направления исследований зависит от способности выйти за рамки существующих парадигм. Если система не поддаётся взлому — значит, мы её ещё недостаточно поняли. Истинное понимание сильно коррелированных материалов требует не просто улучшения существующих методов, но и поиска принципиально новых подходов к описанию квантовой материи.

Оригинал статьи: https://arxiv.org/pdf/2512.23237.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2025-12-31 10:07