Обучение с учетом издержек переключения: новый подход к управлению динамическими системами

Автор: Денис Аветисян

В статье представлена инновационная методика онлайн-обучения, позволяющая оптимизировать поведение систем с неизвестными параметрами и значительными затратами на смену режимов работы.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал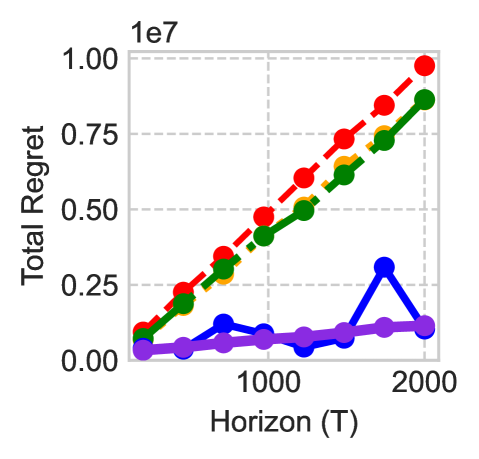

В данной работе алгоритмы SCaLE и HySCaLE демонстрируют свою эффективность, превосходя показатели, достигнутые в оптимизации на основе сглаживания (FTM) по Zhang et al. (2021), а также в задачах онлайн-обучения с зашумленными (POL) и идеальными (OAL) данными.

Алгоритм SCaLE минимизирует суммарные издержки и обеспечивает гарантированно суб-линейную скорость обучения даже в условиях неполной наблюдаемости и вырожденных систем.

Несмотря на успехи в онлайн-обучении с подкреплением, учет затрат на переключение между действиями в динамических системах остается сложной задачей. В данной работе представлена новая методика, SCaLE: Switching Cost aware Learning and Exploration, предназначенная для минимизации динамического сожаления в задачах онлайн-оптимизации с бандитной обратной связью, где присутствуют квадратичные затраты и значительные издержки переключения. Предложенный алгоритм впервые обеспечивает гарантированно суб-линейное сожаление без предварительных знаний о структуре затрат, даже в условиях неполной ранговой определенности. Сможет ли SCaLE стать основой для разработки более эффективных стратегий управления и обучения в сложных, постоянно меняющихся средах?

Задача Последовательного Принятия Решений: Суть Проблемы

Многие задачи, с которыми сталкивается современный мир — от управления робототехникой и финансового моделирования до разработки стратегий в играх и оптимизации логистических цепочек — требуют принятия последовательных решений в условиях неопределенности. В таких сценариях невозможно заранее предвидеть все последствия каждого действия, и успех зависит от способности системы эффективно обучаться на протяжении всего процесса. Это означает, что алгоритм должен не просто выбирать оптимальное действие в текущий момент, но и адаптироваться к изменяющейся обстановке, извлекая уроки из предыдущих решений и корректируя свою стратегию. Разработка эффективных стратегий обучения, способных справляться с этой сложностью, является ключевой задачей в области искусственного интеллекта и машинного обучения, поскольку она позволяет создавать системы, способные к автономному и адаптивному поведению в реальных, динамичных условиях.

В задачах последовательного принятия решений, классические алгоритмы часто сталкиваются с фундаментальной проблемой — необходимостью балансировать между исследованием новых возможностей и использованием уже накопленных знаний. Этот компромисс, известный как дилемма исследования и использования, заключается в том, что чрезмерный акцент на исследовании может привести к упущению оптимальных решений, в то время как чрезмерная эксплуатация существующих знаний может заблокировать поиск более эффективных стратегий. Эффективное решение данной дилеммы требует от алгоритма способности адекватно оценивать потенциальную выгоду от исследования новых вариантов, сопоставляя ее с текущей уверенностью в оптимальности известных решений. Неспособность правильно оценить этот баланс может существенно снизить общую производительность алгоритма в динамической и неопределенной среде.

Эффективность алгоритмов последовательного принятия решений напрямую зависит от точности оценки затрат и способности адаптироваться к ограниченному объему обратной связи. Неточные оценки стоимости могут привести к принятию неоптимальных решений, даже если алгоритм в целом хорошо спроектирован. Более того, в реальных сценариях часто доступна лишь частичная информация о последствиях каждого действия, что усложняет процесс обучения. Алгоритмы, способные эффективно экстраполировать из ограниченных данных и учитывать неопределенность в оценках затрат, демонстрируют значительно более высокую производительность в динамичных и сложных средах. Именно поэтому, современные исследования уделяют особое внимание разработке методов, позволяющих минимизировать влияние неточностей и максимизировать полезность получаемой обратной связи, что является ключевым фактором для успешного применения этих алгоритмов на практике.

Недостаточная ранговая определенность препятствует точной оценке кривизны.

SCaLE: Статистически Согласованный Подход к Оптимизации

Алгоритм SCaLE представляет собой основу для онлайн-оптимизации выпуклых функций, позволяющую эффективно обучаться в задачах последовательного принятия решений. В отличие от традиционных методов, требующих полного набора данных, SCaLE обрабатывает информацию последовательно, обновляя свою стратегию после каждого взаимодействия со средой. Это особенно полезно в динамических средах, где оптимальная политика может меняться со временем. Алгоритм позволяет находить решения для задач, где целевая функция является выпуклой, а ограничения линейными, что обеспечивает гарантированную сходимость к оптимальному решению при достаточном количестве данных. В контексте обучения с подкреплением, SCaLE может быть использован для аппроксимации функции ценности или для непосредственного обучения политике, минимизируя функцию потерь, соответствующую ожидаемым наградам.

Алгоритм SCaLE использует минимизацию следового нормирования (trace-norm minimization) для оценки неизвестной матрицы издержек $C$ . Данный подход позволяет получить приближение к оптимальной матрице издержек на основе наблюдаемых данных, что критически важно для определения оптимальных действий в задачах онлайн-оптимизации. Минимизация следового нормирования является методом регуляризации, способствующим получению разреженных оценок матрицы $C$ , что улучшает обобщающую способность алгоритма и способствует более эффективному определению оптимальной стратегии действий.

Алгоритм SCaLE разработан для обеспечения статистической согласованности, что означает его сходимость к истинной оптимальной политике по мере увеличения объема данных. Это свойство гарантируется благодаря минимизации ошибки оценки матрицы издержек и асимптотическому достижению нулевой потери, что подтверждается теоретическими гарантиями сходимости, зависящими от скорости обучения и свойств данных. Практически, это выражается в том, что при достаточном количестве примеров, решения, принимаемые SCaLE, будут все ближе и ближе к оптимальным, минимизируя кумулятивные издержки в задачах последовательного принятия решений.

Влияние Структуры Матрицы Издержек на Эффективность Алгоритмов

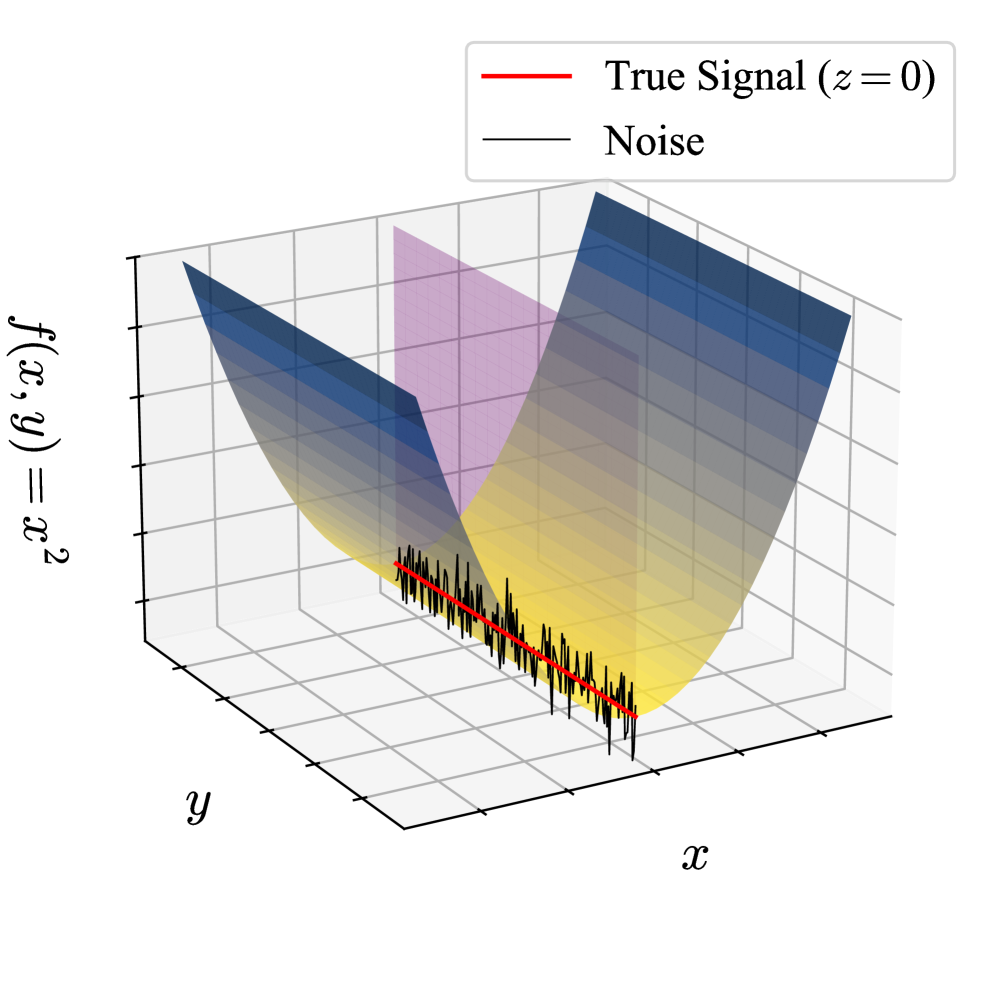
Эффективность алгоритмов, таких как SCaLE, напрямую зависит от структуры матрицы затрат, в частности, от наличия в ней рангодефицитных матриц. Рангодефицитность возникает, когда столбцы матрицы линейно зависимы, что приводит к неопределенности в оценке оптимальных действий. В таких случаях стандартные методы решения задач оптимизации могут давать неточные или неоптимальные результаты, поскольку алгоритм не может однозначно определить наилучший вариант из множества равноценных. Влияние рангодефицитности усиливается при увеличении размерности матрицы и сложности задачи, что требует разработки специальных алгоритмов, устойчивых к таким особенностям структуры матрицы затрат. $\text{rank}(A) < min(m, n)$ , где A — матрица затрат, m — количество строк, n — количество столбцов.

Неточно оцененная матрица затрат приводит к принятию неоптимальных решений и увеличению сожаления — кумулятивной разницы между производительностью алгоритма и оптимальной политикой. Сожаление, в данном контексте, представляет собой меру потерь, возникающих из-за использования субоптимальной стратегии выбора действий. Чем выше значение сожаления, тем значительнее отклонение производительности алгоритма от теоретически возможного максимума, достигаемого при использовании идеальной информации о затратах. В практических приложениях, неточности в оценке матрицы затрат могут возникать из-за шума в данных, неполной информации или ошибок моделирования, что непосредственно влияет на эффективность алгоритма и качество принимаемых решений.

В данной работе получен предел сожаления $𝒪(T^(2/3))$ для алгоритмов, работающих в условиях рангодефицитных матриц издержек. Это демонстрирует сублинейное динамическое сожаление, что означает, что сожаление растет медленнее, чем линейно, по мере увеличения горизонта планирования $T$ . Полученный результат представляет собой значительное улучшение по сравнению с существующими алгоритмами, работающими в условиях ограниченной информации, поскольку традиционные подходы часто демонстрируют более высокие темпы роста сожаления или требуют дополнительных предположений о структуре матрицы издержек.

Модели SCaLE и HySCaLE демонстрируют сопоставимые результаты при [latex]r=1[/latex], [latex]d=4[/latex], [latex]\bar{\eta}=50[/latex], [latex]c=10[/latex] и шуме скорости [latex]v\\_{t}-v\\_{t-1}\\sim\\mathcal{N}(0,50\\cdot I)[/latex], при этом значения [latex]\sigma\\_{r}^{A}[/latex] равные [latex]10^{-2}[/latex] и 1 приводят к аналогичным результатам. — Модели SCaLE и HySCaLE демонстрируют сопоставимые результаты при $r=1$ , $d=4$ , $\bar{\eta}=50$ , $c=10$ и шуме скорости $v\\_{t}-v\\_{t-1}\\sim\\mathcal{N}(0,50\\cdot I)$ , при этом значения $\sigma\\_{r}^{A}$ равные $10^{-2}$ и 1 приводят к аналогичным результатам.

HySCaLE: Непрерывная Корректировка для Повышенной Эффективности

Алгоритм HySCaLE развивает подход SCaLE путем интеграции метода проекционного градиентного спуска для непрерывной корректировки оценки матрицы издержек. В отличие от статических оценок, используемых в SCaLE, HySCaLE динамически обновляет значения матрицы издержек на основе наблюдаемых данных и текущего состояния среды. Это достигается путем итеративного применения проекционного градиентного спуска к функции потерь, которая измеряет расхождение между предсказанными и фактическими издержками. Проекция гарантирует, что обновленные оценки останутся в допустимом диапазоне, предотвращая расходимость и обеспечивая стабильность алгоритма. Такой подход позволяет HySCaLE более точно моделировать издержки, связанные с принятием решений, и улучшать производительность в динамических условиях.

Алгоритм HySCaLE обеспечивает адаптацию к изменяющимся условиям среды посредством непрерывной корректировки оценки матрицы стоимостей. Этот процесс позволяет системе динамически подстраивать свою стратегию выбора действий в ответ на поступающую информацию о текущей обстановке. Корректировка осуществляется путем итеративного применения метода стохастического градиентного спуска, что позволяет минимизировать ошибку оценки и повысить точность принимаемых решений. В результате, HySCaLE демонстрирует улучшенную производительность в нестабильных средах по сравнению с алгоритмами, использующими статическую оценку стоимостей, и обеспечивает более эффективное управление балансом между исследованием новых возможностей и затратами на переключение между ними.

Алгоритм HySCaLE демонстрирует сублинейную границу сожаления $O(\sqrt{T}\log T)$ , что подтверждает его оптимальность в задачах принятия решений в условиях неопределенности. Данный результат, полученный посредством теоретического анализа и подтвержденный эмпирическими данными, свидетельствует об эффективном балансе между стоимостью исследования (exploration) и стоимостью переключения (switching costs). В отличие от методов, использующих статическую оценку стоимости, HySCaLE динамически адаптирует свою стратегию, минимизируя кумулятивные потери и обеспечивая высокую производительность даже в изменяющихся условиях среды.

Представленная работа демонстрирует стремление к элегантности в решении сложной задачи — минимизации сожаления в динамических системах с неизвестными функциями затрат. Алгоритм SCaLE, в своей основе, отражает философию отказа от избыточности, концентрируясь на эффективном балансе между исследованием и использованием доступных данных. В этом контексте, особенно уместны слова Линуса Торвальдса: «Если вы не стыдитесь своего кода через пару недель, значит, вы не достаточно хорошо программируете». Схожим образом, SCaLE стремится к простоте и эффективности, избегая ненужных усложнений в управлении системами с функциями квадратичных затрат и значительными издержками переключения, даже в условиях неполной определенности ранга.

Куда Дальше?

Представленный алгоритм SCaLE, несомненно, демонстрирует элегантность в разрешении задачи минимизации сожаления в динамических системах с затратами на переключение. Однако, упрощение — это не всегда истина. Гарантии сублинейного сожаления в условиях неопределенности затрат и неполноты ранга — это достижение, но стоит помнить: реальный мир редко бывает столь послушным. Ограничение на квадратичные затраты — это не столько принципиальное ограничение алгоритма, сколько признание его текущей неспособности к более общему описанию. Следующим шагом видится расширение класса поддерживаемых функций затрат, возможно, в сторону негладких или неквадратичных.

Более того, анализ алгоритма предполагает стационарность динамики системы. В реальности же, системы постоянно эволюционируют. Изучение адаптации SCaLE к изменяющимся динамическим моделям, возможно, с использованием рекуррентных нейронных сетей для оценки этих изменений, представляется перспективным направлением. Важно помнить: предсказание будущего — занятие неблагодарное, но попытки понять его структуру — необходимы.

И наконец, вопрос о вычислительной сложности. Элегантность алгоритма не должна затмевать необходимость его практической реализации. Оптимизация кода и разработка параллельных алгоритмов для обработки больших объемов данных станут ключевыми факторами для внедрения SCaLE в реальные системы управления. Простота — высшая форма сложности, а код должен быть очевиден, как гравитация.

Оригинал статьи: https://arxiv.org/pdf/2601.09042.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-15 20:36