Управляемые потоки: новый подход к генерации данных с ограничениями

Автор: Денис Аветисян

Исследователи предложили инновационный метод, использующий принципы оптимального управления для создания генеративных моделей, способных точно соответствовать заданным условиям.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал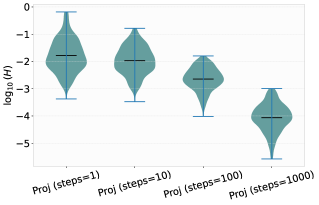

Представленное исследование демонстрирует, что алгоритм TOCFlow значительно превосходит базовые методы в минимизации нарушений ограничений и чувствительности к гиперпараметрам, причём его производительность резко возрастает при увеличении числа шагов явного метода Эйлера до значений больше единицы, в то время как другие методы либо деградируют, либо демонстрируют незначительное улучшение, а дальнейшее увеличение числа итераций терминальной проекции, хоть и снижает ошибку, не позволяет достичь сопоставимых результатов с TOCFlow.

В работе представлена структура TOCFlow, формулирующая обеспечение ограничений в потоковых генеративных моделях как задачу оптимального управления в терминальной фазе.

Наложение сложных ограничений на генеративные модели, основанные на потоках, представляет собой нетривиальную задачу, требующую баланса между соблюдением условий и сохранением качества генерируемых данных. В данной работе, ‘Terminally constrained flow-based generative models from an optimal control perspective’, предложен новый подход, формулирующий задачу как оптимальное терминальное управление, что позволяет эффективно накладывать ограничения различного типа. Разработанный метод TOCFlow обеспечивает геометрическую согласованность и высокую эффективность при генерации выборок, удовлетворяющих заданным условиям, без значительных вычислительных затрат. Возможно ли дальнейшее расширение предложенного подхода для решения еще более сложных задач генеративного моделирования с учетом разнообразных ограничений и требований?

За гранью диффузии: Поиск управляемого генеративного процесса

Диффузионные модели, демонстрирующие впечатляющую способность генерировать разнообразные данные, зачастую сталкиваются с трудностями в точном контроле над создаваемыми образцами. Эта особенность становится критичной в приложениях, требующих строгого соблюдения физических законов или заранее заданных конструктивных ограничений. Например, при моделировании молекулярных структур или проектировании инженерных деталей, произвольное отклонение от необходимых параметров недопустимо. Отсутствие возможности точного управления генерацией ограничивает практическое применение диффузионных моделей в областях, где важна не только реалистичность, но и соответствие определённым требованиям и стандартам, что подчёркивает необходимость разработки новых подходов к генеративному моделированию.

Попытки интегрировать ограничения в существующие генеративные модели, такие как диффузионные, часто сталкиваются со значительными трудностями. Традиционные методы, как правило, приводят к снижению качества генерируемых образцов или вызывают нестабильность процесса обучения. В частности, прямое применение штрафных функций или алгоритмов проекции может искажать распределение данных, приводя к нереалистичным или нежелательным результатам. Кроме того, неспособность эффективно балансировать между соблюдением ограничений и сохранением разнообразия образцов приводит к тому, что модель либо игнорирует ограничения, либо генерирует слишком однообразные и предсказуемые результаты. Это требует разработки принципиально новых подходов, которые позволяют нативно поддерживать и обеспечивать соблюдение заданных условий, не жертвуя при этом качеством и креативностью генерируемых данных.

Ограничения существующих генеративных моделей, особенно в контексте соблюдения физических законов или инженерных требований, обуславливают потребность в принципиально новом подходе к генеративному моделированию. Традиционные методы часто сталкиваются с трудностями при интеграции ограничений, приводя к снижению качества генерируемых образцов или нестабильности процесса обучения. Поэтому возникает необходимость в парадигме, которая изначально поддерживает и обеспечивает соблюдение ограничений с высокой точностью и эффективностью, позволяя создавать не только разнообразные, но и соответствующие заданным критериям данные. Такой подход открывает перспективы для решения сложных задач, требующих строгого соответствия определенным правилам и спецификациям, и позволит значительно расширить область применения генеративных моделей в науке и технике.

Сравнение траекторий, сгенерированных различными методами, показывает, что GD и TOCFlow обеспечивают плавное движение в пределах безопасных коридоров, в то время как методы, основанные на проекциях, хоть и строго соблюдают ограничения, приводят к появлению нефизичных разрывов на границах, в отличие от vanilla-метода, часто нарушающего границы допустимой области.

Метод Flow Matching: Управление потоком генерации

Метод Flow Matching рассматривает генерацию данных как задачу обучения обычному дифференциальному уравнению (ОДУ), которое отображает случайный шум в структуру данных. В основе этого подхода лежит идея построения траектории в пространстве данных, начинающейся с шума и заканчивающейся сгенерированной выборкой. Интегрирование этой ОДУ позволяет напрямую и эффективно осуществлять процесс генерации, минуя необходимость в итеративных методах, таких как цепи Маркова, часто используемые в генеративных моделях. Процесс интегрирования $\frac{dx}{dt} = v(x,t)$ определяет эволюцию состояния $x$ во времени $t$ , где $v(x,t)$ — векторное поле скорости, обученное на данных.

В основе метода Flow Matching лежит обучение поля скоростей — функции, определяющей направление и величину перемещения вдоль траектории генерации данных. Это поле скоростей, обозначаемое как $v(x, t)$ , описывает векторное поле в пространстве данных, указывающее, как точка данных должна перемещаться во времени $t$ для достижения желаемого распределения. По сути, поле скоростей преобразует начальное шумовое состояние в целевое распределение данных посредством интегрирования по времени. Обучение этого поля осуществляется путем минимизации расхождения между предсказанным направлением движения и фактическим градиентом плотности вероятности данных, что позволяет создавать плавные и контролируемые траектории генерации.

Обучение поля скоростей соответствию градиенту распределения данных является ключевым аспектом Flow Matching, обеспечивающим плавность и управляемость процесса генерации. Соответствие градиенту позволяет полям скоростей направлять процесс генерации от шума к области высокой плотности данных, избегая резких переходов и локальных минимумов. По сути, поле скоростей действует как векторное поле, указывающее направление наибольшего увеличения плотности вероятности данных в каждой точке пространства шума. Это гарантирует, что траектории интеграции, используемые для генерации данных, следуют по наиболее вероятным путям, что приводит к получению реалистичных и когерентных образцов. Эффективность этого подхода заключается в том, что поле скоростей, обученное таким образом, позволяет контролировать процесс генерации, направляя его по желаемым траекториям и обеспечивая стабильное качество генерируемых данных.

Сравнение сгенерированных полей проницаемости [latex]K[/latex] и давления [latex]p[/latex] различными методами показывает, что градиентный спуск (GD) и TOCFlow смещают распределение невязок в сторону меньших значений, что свидетельствует о более эффективном удовлетворении ограничений. — Сравнение сгенерированных полей проницаемости $K$ и давления $p$ различными методами показывает, что градиентный спуск (GD) и TOCFlow смещают распределение невязок в сторону меньших значений, что свидетельствует о более эффективном удовлетворении ограничений.

TOCFlow: Оптимальное управление для генерации с ограничениями

Метод TOCFlow применяет инновационный подход к обеспечению соблюдения ограничений при генерации, формулируя задачу управления как задачу оптимального управления на терминальной стадии. В основе подхода лежит использование принципов оптимального управления, где целевая функция минимизирует отклонение от заданных ограничений. Вместо традиционных методов, накладывающих ограничения непосредственно на процесс генерации, TOCFlow рассматривает ограничения как терминальные условия, к которым необходимо стремиться в конце процесса. Это позволяет сформулировать задачу как поиск оптимальной траектории, удовлетворяющей этим терминальным условиям, и, следовательно, обеспечить соблюдение ограничений на генерируемых данных.

Формулировка TOCFlow позволяет получить коррекцию поля скоростей, учитывающую геометрию пространства ограничений. Данная коррекция применяется к векторам скорости генерации образцов, обеспечивая их соответствие заданным ограничениям без существенной потери качества. В процессе вычисления коррекции учитывается локальная геометрия области, что позволяет более эффективно направлять процесс генерации в допустимые области, минимизируя отклонения от заданных ограничений и предотвращая генерацию нежелательных образцов. Это достигается путем вычисления оптимальной траектории изменения вектора скорости для каждого образца, с учетом геометрии ограничений и минимизации затрат на управление.

Алгоритм TOCFlow обеспечивает эффективную и стабильную генерацию с ограничениями благодаря оптимизации минимальных затрат на управление для соблюдения заданных ограничений. В рамках данной оптимизации, целевая функция минимизирует величину управляющего воздействия, необходимого для приведения генерируемых образцов в соответствие с ограничениями. В результате, терминальные издержки (terminal costs) TOCFlow оказываются на несколько порядков величины ниже, чем у базовых методов, что подтверждает повышение эффективности и стабильности процесса генерации. Это достигается за счет более точного и экономичного управления процессом, избегая избыточных коррекций и обеспечивая плавное достижение целевых значений в рамках заданных ограничений.

В ходе количественной оценки нарушений ограничений и чувствительности к гиперпараметрам было показано, что TOCFlow значительно снижает нарушения по сравнению с базовыми алгоритмами GD и Vanilla, достигая результатов, сопоставимых с GN и терминальной проекцией, а также обеспечивает терминальную стоимость около [latex]10^{-{12}}[/latex] даже при одном шаге явной схемы Эйлера, существенно превосходя GD, который достигает [latex]10^{-9}[/latex] при восьми шагах. — В ходе количественной оценки нарушений ограничений и чувствительности к гиперпараметрам было показано, что TOCFlow значительно снижает нарушения по сравнению с базовыми алгоритмами GD и Vanilla, достигая результатов, сопоставимых с GN и терминальной проекцией, а также обеспечивает терминальную стоимость около $10^{-{12}}$ даже при одном шаге явной схемы Эйлера, существенно превосходя GD, который достигает $10^{-9}$ при восьми шагах.

Подтверждение эффективности: Тестирование и оценка TOCFlow

Исследования показали, что TOCFlow демонстрирует высокую эффективность в моделировании течения Дарси, что подтверждено серией численных экспериментов. Метод позволяет точно соблюдать ограничения на движение жидкости в пористых средах, обеспечивая значительное — на несколько порядков — снижение величины остаточных невязок по сравнению с традиционными подходами. Такая точность особенно важна при решении задач фильтрации и гидрогеологии, где даже небольшие погрешности могут приводить к существенным ошибкам в прогнозах. Полученные результаты свидетельствуют о превосходстве TOCFlow в задачах, требующих строгого контроля над потоком жидкости в сложных пористых структурах, и открывают новые возможности для повышения надежности и точности моделирования.

Метод TOCFlow был подвергнут проверке на сложных снимках турбулентного потока, демонстрируя свою применимость к многомерным, реалистичным данным. Анализ показал, что полученные результаты точно соответствуют целевому закону масштабирования, что подтверждает способность метода адекватно моделировать сложные гидродинамические процессы. Такое соответствие имеет важное значение для точного прогнозирования поведения турбулентных потоков в различных инженерных приложениях и научных исследованиях, поскольку позволяет эффективно учитывать нелинейные взаимодействия и сложные зависимости в данных.

Для повышения эффективности и масштабируемости разработанного подхода активно применялись методы понижения метрики до постоянной величины и автоматического дифференцирования. Постоянная метрика позволяет значительно упростить вычислительные процедуры, снижая сложность алгоритма и потребность в ресурсах. В свою очередь, автоматическое дифференцирование обеспечивает точное и эффективное вычисление градиентов, необходимых для оптимизации и решения задач в высокоразмерных пространствах. Комбинация этих техник не только ускоряет процесс вычислений, но и позволяет применять данный подход к более сложным и масштабным задачам, связанным с моделированием потоков в пористых средах и анализом турбулентных данных.

Сравнение визуализации турбулентности, полученной различными методами, демонстрирует различия в структуре и деталях потока между подходами vanilla, GD, TOCFlow, аппроксимированным GN и терминальной проекцией.

Взгляд в будущее: Расширяя границы генерации с ограничениями

Разработанная схема обладает значительным потенциалом для дальнейшего развития, позволяя интегрировать более сложные ограничения и целевые функции. Это открывает возможности для генерации данных, характеризующихся повышенным реализмом и точностью управления. В частности, введение нелинейных ограничений, учитывающих физические свойства моделируемых объектов или специфические требования к генерируемым данным, позволит создавать более правдоподобные и функциональные результаты. Более того, использование многоцелевых функций, учитывающих различные аспекты качества генерируемых данных, например, точность, гладкость и разнообразие, способствует достижению оптимального баланса между этими характеристиками и, как следствие, получению более полезных и применимых данных для широкого спектра задач, от компьютерного зрения до разработки новых материалов.

Исследование проксимальных операторов открывает перспективные пути для повышения устойчивости и надёжности процесса оптимизации в задачах генерации с ограничениями. Эти операторы, в отличие от традиционных методов, обеспечивают более плавный переход к оптимальному решению, минимизируя риск отклонения от заданных границ и предотвращая колебания. Применение проксимальных операторов позволяет эффективно обрабатывать сложные и шумные данные, а также гарантирует сходимость алгоритма даже при наличии неидеальных начальных условий. $\text{prox}_{\gamma f}(x) = \text{arg min}_y \{\frac{1}{2}||y-x||_2^2 + \gamma f(y) \}$ — данная формула демонстрирует принцип работы проксимального оператора, где γ — параметр, контролирующий степень приближения к оптимальному решению. Подобный подход особенно важен для приложений, требующих высокой точности и предсказуемости, например, в задачах управления роботами и автоматической навигации.

Сочетание алгоритма TOCFlow с алгоритмами планирования траектории открывает новые горизонты в таких областях, как робототехника и автономная навигация. TOCFlow, обеспечивая генерацию реалистичных и контролируемых данных, может служить основой для создания более эффективных и адаптивных систем управления движением роботов. В частности, интеграция позволяет решать сложные задачи планирования траектории, учитывая множество ограничений и целей, например, обход препятствий, оптимизацию энергопотребления или соблюдение заданных временных рамок. Подобный симбиоз алгоритмов позволяет создавать роботов, способных автономно ориентироваться в сложных средах, выполнять сложные манипуляции и эффективно взаимодействовать с окружающим миром, что особенно важно для применения в логистике, поисково-спасательных операциях и других критически важных областях.

Сравнительный анализ демонстрирует, что методы GD и TOCFlow значительно превосходят стандартные подходы и проекцию в терминальном состоянии по минимизации терминальной стоимости [latex]H(\bm{x})[/latex], при этом чувствительность к числу шагов явной схемы Эйлера у них схожа, в отличие от терминальной проекции, чья ошибка остаётся высокой независимо от количества итераций. — Сравнительный анализ демонстрирует, что методы GD и TOCFlow значительно превосходят стандартные подходы и проекцию в терминальном состоянии по минимизации терминальной стоимости $H(\bm{x})$ , при этом чувствительность к числу шагов явной схемы Эйлера у них схожа, в отличие от терминальной проекции, чья ошибка остаётся высокой независимо от количества итераций.

Исследование представляет собой элегантную попытку взглянуть на генеративные модели с точки зрения оптимального управления. Авторы, по сути, предлагают рассматривать задачу обеспечения соответствия с ограничениями как задачу оптимального управления в терминальной фазе. Это позволяет применять инструменты из теории оптимального управления для решения проблемы генерации данных, удовлетворяющих сложным условиям. В контексте этого подхода особенно примечательна фраза Джона Маккарти: «Всякий интеллект — это способность видеть возможности, а не только препятствия». Действительно, представленный метод TOCFlow демонстрирует именно это — способность увидеть возможности в ограничениях, превращая их из препятствий в неотъемлемую часть процесса генерации, что особенно важно для достижения геометрической согласованности и эффективности, о которых говорится в работе.

Что Дальше?

Представленный подход, формулируя обеспечение ограничений в потоковых генеративных моделях как задачу оптимального управления, неизбежно наталкивается на вечную проблему: стоимость вычислений. Каждый «патч», каждая оптимизация — это признание несовершенства алгоритма, его неспособности к идеальной генерации с первого раза. Впрочем, это и хорошо — осознание границ системы всегда интереснее иллюзии всемогущества. Следующим шагом видится разработка более эффективных решателей для связанных уравнений Беллмана и Гамильтона-Якоби, возможно, с использованием техник редукции размерности или стохастических методов.

Более глубокое исследование геометрических свойств полученных потоков представляется перспективным направлением. Как именно наложенные ограничения деформируют пространство латентных переменных? Можно ли использовать эти деформации для целенаправленного управления генерацией, «взлома» системы, чтобы получить желаемые образцы? В конечном счете, суть не в создании идеального генератора, а в понимании того, как он работает, и умении его обходить.

Очевидным расширением является применение данного подхода к задачам, где ограничения не являются жесткими, а задаются в виде мягких штрафов или вероятностных ограничений. Это потребует разработки новых методов регуляризации и адаптации алгоритмов обучения. Лучший хак — это осознанность того, как всё работает, а каждый «патч» — философское признание несовершенства.

Оригинал статьи: https://arxiv.org/pdf/2601.09474.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-16 03:21