Риск под контролем: Как не прогадать при неверных предположениях

от

Автор: Денис Аветисян

Новое исследование показывает, что для оценки рисков в условиях неопределенности важно учитывать возможность ошибок в исходных моделях.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал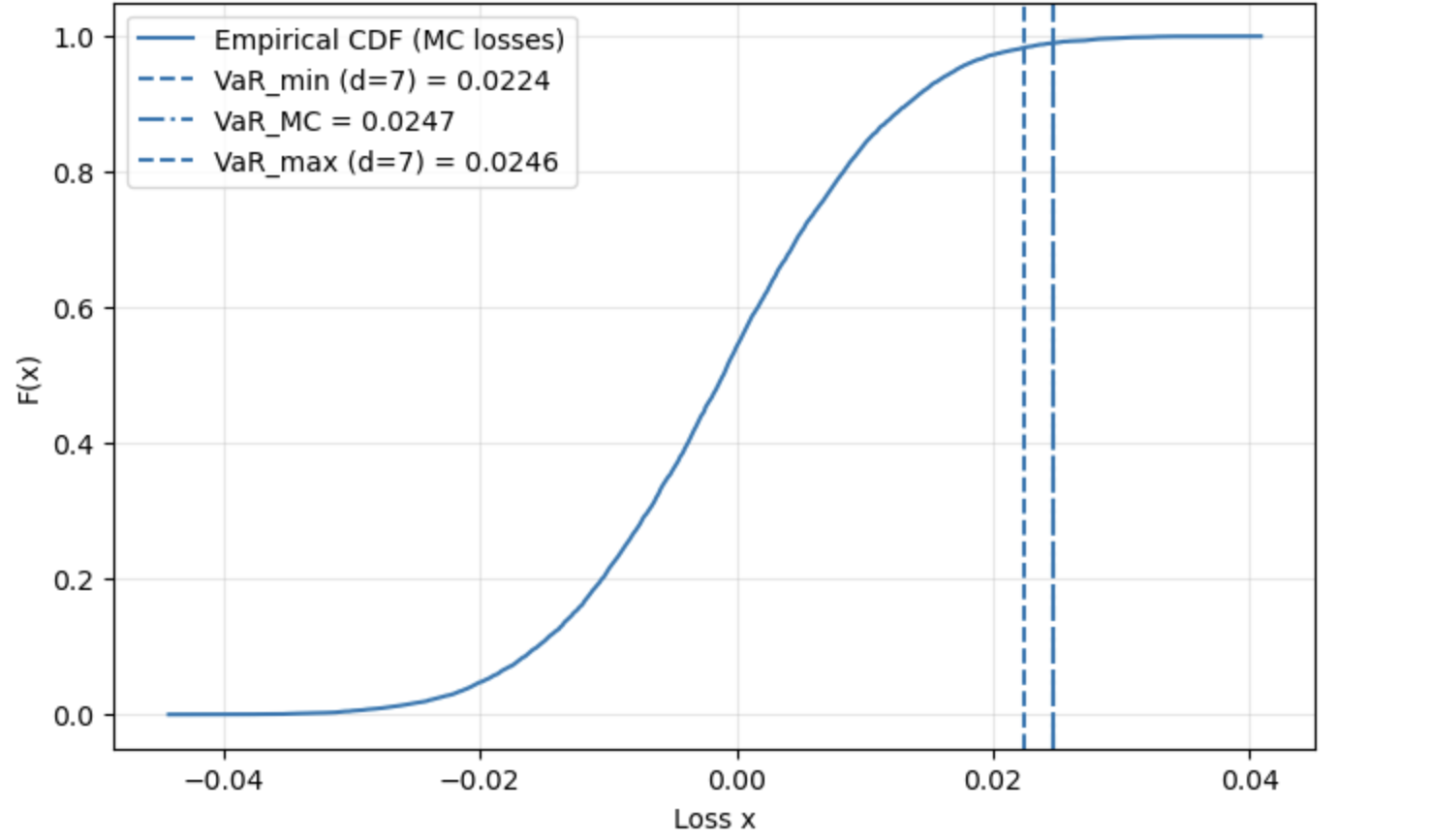
В рамках исследования демонстрируется, что интервалы VaR, рассчитанные с учетом моментальных ограничений, эффективно ограничивают эмпирическую функцию распределения потерь при уровне доверия 0.99, при этом верхняя и нижняя границы VaR, определяемые методом моментов, согласуются с эталонным значением, полученным методом Монте-Карло.
В рамках исследования демонстрируется, что интервалы VaR, рассчитанные с учетом моментальных ограничений, эффективно ограничивают эмпирическую функцию распределения потерь при уровне доверия 0.99, при этом верхняя и нижняя границы VaR, определяемые методом моментов, согласуются с эталонным значением, полученным методом Монте-Карло.

Сравнение эффективности методов Importance Sampling и дискретного сопоставления моментов для оценки Value-at-Risk при неверной спецификации распределения хвостов.

Оценка риска убытков в периоды экстремальных событий представляет собой сложную задачу, особенно чувствительную к поведению “хвостов” распределения и неточности используемых моделей. В работе ‘Efficiency versus Robustness under Tail Misspecification: Importance Sampling and Moment-Based VaR Bracketing’ исследуется эффективность двух подходов к симуляционному оцениванию Value-at-Risk — importance sampling и дискретного сопоставления моментов — при контролируемом искажении характеристик “хвостов”. Полученные результаты демонстрируют, что, хотя importance sampling обеспечивает высокую точность при корректных предположениях о распределении, дискретное сопоставление моментов предоставляет более надежную, хотя и менее точную, оценку VaR при наличии неопределенности в форме распределения. Действительно ли снижение дисперсии является достаточным условием для надежной оценки экстремальных рисков в условиях модельной неопределенности?

Оценка Риска: Иллюзия Точности VaR

Риск-менеджмент в финансовой сфере опирается на показатель Value at Risk (VaR) как на ключевой инструмент оценки потенциальных потерь. Однако, несмотря на широкое применение, точное вычисление VaR представляет собой сложную задачу. Суть проблемы заключается в том, что VaR требует прогнозирования вероятности наступления экстремальных событий, что связано с неопределенностью и зависимостью от используемых моделей. Даже небольшие погрешности в оценке параметров этих моделей могут привести к существенным искажениям в расчете VaR, а следовательно, и к недооценке или переоценке рисков. Поэтому, несмотря на свою кажущуюся простоту, VaR требует постоянного совершенствования методик и учета особенностей конкретных финансовых инструментов и рыночных условий.

Традиционные методы расчета Value at Risk (VaR) часто опираются на предположения о распределении данных, что может приводить к существенным ошибкам в оценке рисков. Особенно критична проблема при работе с распределениями, имеющими «тяжелые хвосты» — то есть, с повышенной вероятностью экстремальных событий. В таких случаях стандартные статистические модели, предполагающие нормальное распределение, недооценивают вероятность наступления крупных потерь, поскольку не учитывают высокую концентрацию вероятности в области экстремальных значений. Неправильная спецификация модели, игнорирующая особенности распределения, приводит к заниженной оценке VaR, создавая иллюзию меньшего риска, чем он есть на самом деле. Это может привести к недостаточной капитализации и, как следствие, к серьезным финансовым потерям в периоды рыночной турбулентности. VaR = \mu - z\sigma , где μ — среднее значение, σ — стандартное отклонение, а z — квантиль нормального распределения, — эта формула наглядно демонстрирует зависимость VaR от предположения о нормальности распределения.

Оценка величины VaR (Value at Risk) часто требует проведения сложных вычислительных симуляций, особенно при анализе редких событий, способных привести к значительным финансовым потерям. Это связано с тем, что стандартные аналитические методы оказываются неэффективными при моделировании экстремальных сценариев, а для точной оценки вероятности их наступления необходимо моделировать большое количество возможных траекторий развития рынка. В частности, методы Монте-Карло, предполагающие многократное случайное моделирование, становятся необходимыми для получения надежных оценок VaR в условиях неопределенности. Вычислительная сложность подобных симуляций возрастает экспоненциально с увеличением количества учитываемых факторов риска и горизонтом прогнозирования, что требует использования мощных вычислительных ресурсов и разработки эффективных алгоритмов для оптимизации процесса моделирования. VaR = \mu - z\sigma , где μ — средняя доходность, σ — стандартное отклонение, а z — значение, соответствующее заданному уровню доверия.

Калибровка IS VaR с использованием t-распределения показывает, что выборочное среднее VaR часто занижает истинное значение, о чем свидетельствует точки ниже линии идентичности.
Калибровка IS VaR с использованием t-распределения показывает, что выборочное среднее VaR часто занижает истинное значение, о чем свидетельствует точки ниже линии идентичности.

Метод Монте-Карло и Искусство Выборки

Метод Монте-Карло предоставляет гибкую основу для оценки ценности под риском (VaR), однако стандартные методы моделирования могут оказаться неэффективными при оценке вероятностей редких событий. Это связано с тем, что для точной оценки вероятности крайне малых значений потерь требуется очень большое количество симуляций, что требует значительных вычислительных ресурсов. В частности, при моделировании «тяжелых хвостов» распределения, стандартные методы Монте-Карло демонстрируют низкую скорость сходимости, требуя экспоненциально возрастающего числа симуляций для достижения приемлемой точности. Это делает их практически неприменимыми для оценки рисков, связанных с экстремальными рыночными условиями, где вероятность наступления неблагоприятных событий крайне мала.

Метод значимой выборки (Importance Sampling) представляет собой технику снижения дисперсии, направленную на повышение эффективности оценки вероятностей редких событий. Вместо равномерной выборки из всего пространства распределения, данный метод концентрирует вычислительные усилия на наиболее критичных областях, где вероятность наступления события наиболее высока. Это достигается за счет использования альтернативного распределения выборки, которое позволяет чаще генерировать значения в интересующих областях, тем самым снижая вариативность оценки и повышая точность при заданном объеме вычислений. Эффективность метода напрямую зависит от правильного выбора функции значимости, определяющей форму нового распределения выборки.

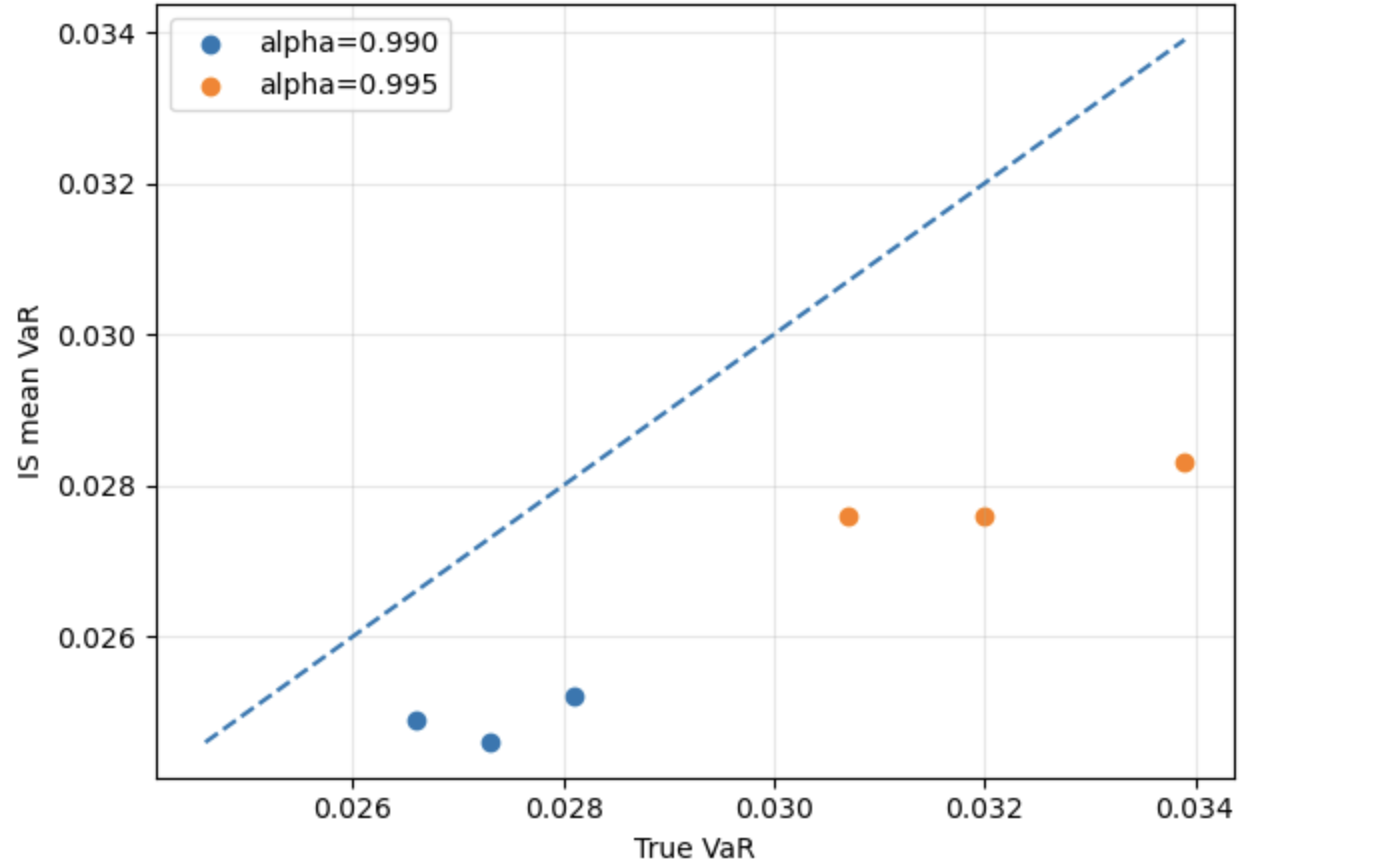
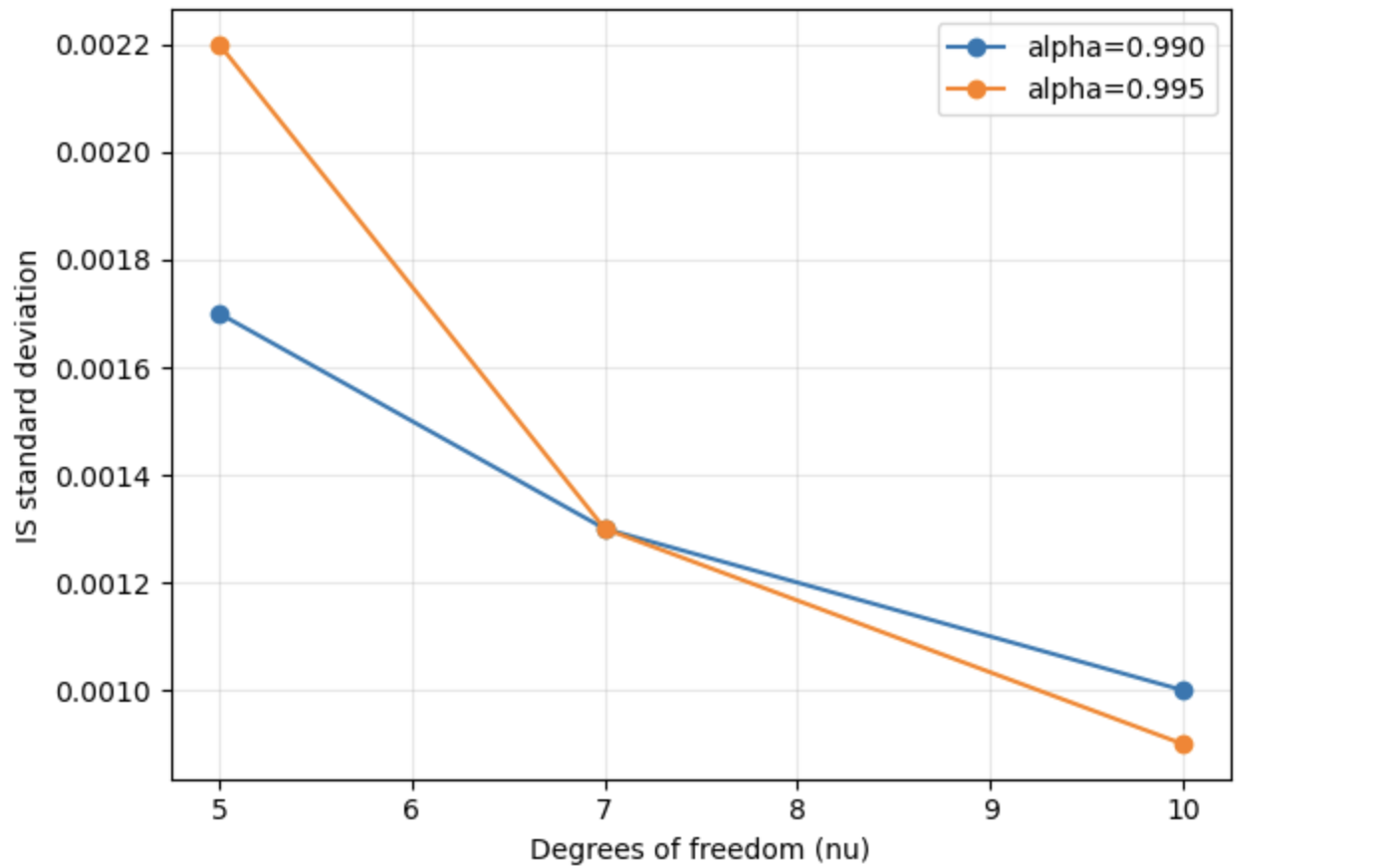
Эффективная реализация метода важности (Importance Sampling, IS) требует тщательного выбора распределения выборки и использования техник, таких как экспоненциальное смещение (exponential tilting). Однако, проведенное исследование показывает, что при использовании распределений, имеющих тяжелые хвосты, подобных распределению Стьюдента (Student-t), IS систематически занижает оценку риска, демонстрируя отрицательную смещенность (negative bias). Это связано с тем, что стандартные методы важности недостаточно эффективно исследуют области высокой вероятности в хвостах распределения, приводя к недооценке вероятности экстремальных событий и, следовательно, к заниженной оценке Value at Risk (VaR).

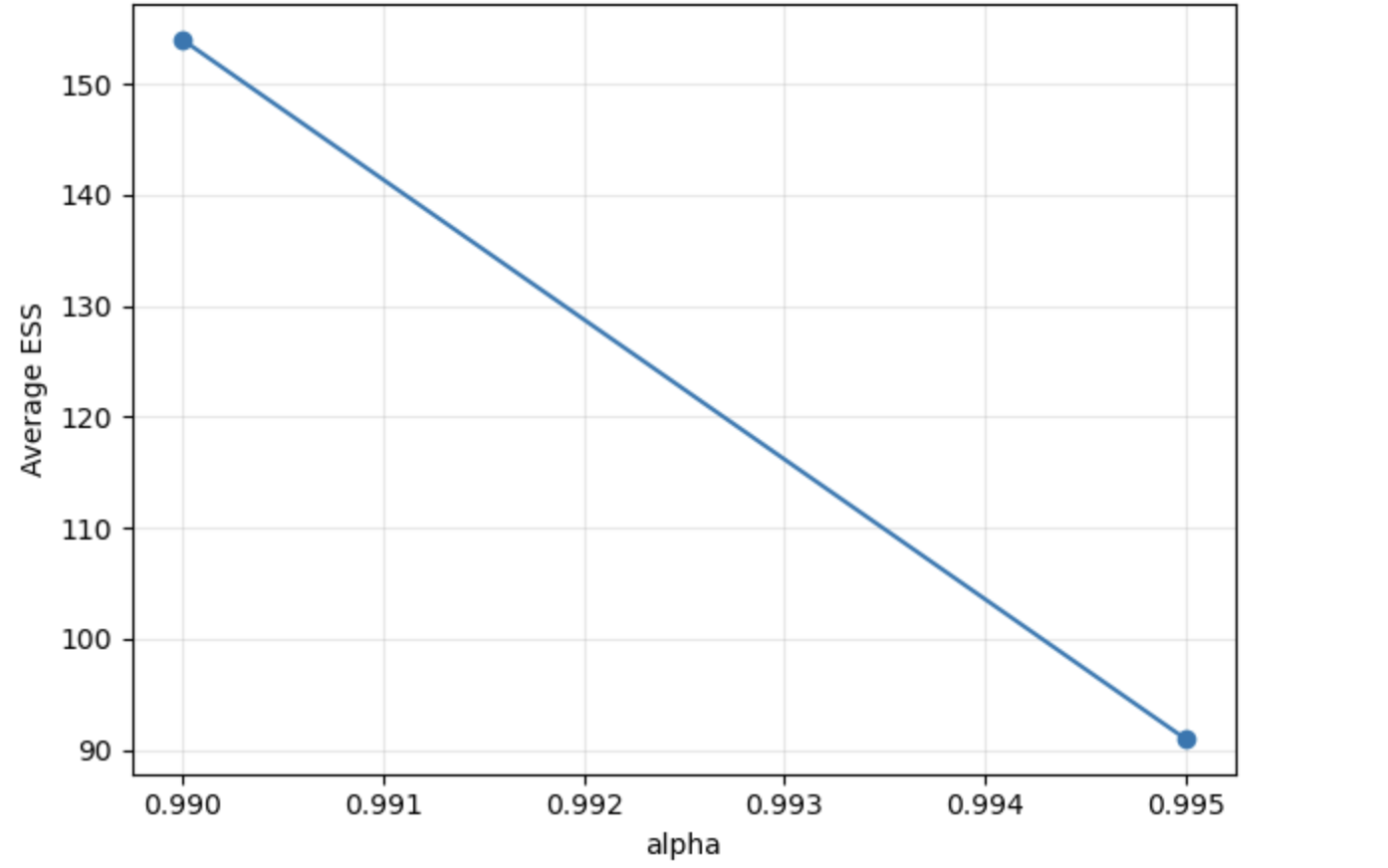
Эффективный размер выборки (ESS) снижается с повышением уровня доверия при использовании метода значимости выборки. В ходе исследования установлено, что при уровне доверия α=0.990 ESS составляет приблизительно 154, в то время как при повышении уровня доверия до α=0.995, ESS снижается до примерно 91. Данное снижение указывает на уменьшение соответствия между мерой, используемой при значимости выборки, и истинной геометрией хвоста распределения, что приводит к снижению точности оценки рисков на высоких уровнях доверия. Это свидетельствует о том, что значимость выборки становится менее эффективной при оценке редких событий, соответствующих высоким уровням доверия.

За пределами предположений: Дискретное Сопоставление Моментов

Метод дискретного сопоставления моментов (Discrete Moment Matching, DMM) позволяет вычислять VaR (Value at Risk) без необходимости предположений о конкретном параметрическом распределении базового актива. В отличие от традиционных методов, которые требуют задания нормального, t-распределения или других параметрических моделей, DMM основывается на установлении ограничений на моменты распределения вероятностей. Это достигается путем определения моментов, таких как среднее значение, дисперсия, асимметрия и эксцесс, и последующего построения интервала, гарантированно содержащего истинное значение VaR, независимо от фактической формы распределения. Такой подход особенно полезен в ситуациях, когда форма распределения неизвестна или подвержена изменениям, обеспечивая более надежную оценку риска по сравнению с методами, полагающимися на конкретные параметрические предположения.

Метод сопоставления дискретных моментов (Discrete Moment Matching, DMM) позволяет получать границы для расчета VaR (Value at Risk) путем наложения ограничений на моменты распределения. Вместо предположения о конкретной параметрической форме распределения, DMM использует моменты — среднее, дисперсию, асимметрию, эксцесс и т.д. — для определения допустимого диапазона значений VaR. При этом, накладывая ограничения на эти моменты, достигается устойчивость к ошибкам спецификации модели, поскольку расчет VaR не зависит от конкретного выбранного распределения, а основывается на фундаментальных статистических характеристиках. Ширина интервала, полученного с помощью DMM, уменьшается с увеличением порядка моментов (до d=7), после чего стабилизируется, что указывает на снижение неопределенности и сужение границ оценки VaR.

Метод дискретного сопоставления моментов (DMM) обеспечивает получение надежных оценок риска даже при неизвестном истинном распределении. Ширина интервала, полученного с помощью DMM, закономерно уменьшается с увеличением порядка моментов, используемых в ограничении (до d=7), после чего стабилизируется. Данная закономерность свидетельствует о снижении неопределенности и уточнении границ оценки VaR, поскольку с каждым добавленным моментом повышается точность моделирования распределения и, соответственно, сужается интервал возможных значений риска. Стабилизация интервала после d=7 указывает на достижение точки, после которой добавление дополнительных моментов не приводит к существенному улучшению точности оценки.

Исследования показали, что дискретное сопоставление моментов (DMM) дает консервативные оценки VaR, то есть, как правило, завышает уровень риска. Однако, эта консервативность обеспечивает повышенную надежность при работе с распределениями с “тяжелыми хвостами” (heavy-tailed distributions), где вероятность экстремальных событий выше, и в условиях неверной спецификации модели. В ситуациях, когда предположения о форме распределения активов не соответствуют действительности, DMM демонстрирует устойчивость и позволяет получить более достоверные оценки риска по сравнению с традиционными параметрическими методами, несмотря на более широкие интервалы.

Вариация границ VaR, рассчитанных методом DMM, с увеличением порядка моментов [latex]dd[/latex] приводит к возрастанию и стабилизации нижней границы, в то время как верхняя граница остается практически неизменной.
Вариация границ VaR, рассчитанных методом DMM, с увеличением порядка моментов dd приводит к возрастанию и стабилизации нижней границы, в то время как верхняя граница остается практически неизменной.

Оптимизация Эффективности: Ключевые Моменты

Эффективность метода важностной выборки (Importance Sampling, IS) напрямую зависит от ряда ключевых факторов, среди которых особое значение имеют отношение правдоподобия и номинальная модель. Отношение правдоподобия, представляющее собой соотношение плотностей вероятности истинного и предлагаемого распределений, определяет вес, присваиваемый каждой выборке. Неточности в номинальной модели, используемой для приближения истинного распределения, приводят к искажению этих весов и, как следствие, к снижению точности оценки. Таким образом, тщательный выбор номинальной модели и корректная оценка отношения правдоподобия являются критически важными для достижения высокой эффективности и надежности результатов, получаемых с помощью IS. Отклонение номинальной модели от реальности может приводить к концентрации весов, что, в свою очередь, уменьшает эффективность метода и требует дополнительных мер для стабилизации оценки.

Концентрация весов в выборке, полученной методом значимой выборки, может существенно повлиять на точность получаемых оценок, что требует постоянного контроля. Высокая концентрация весов указывает на то, что небольшое число выборок вносит непропорционально большой вклад в итоговую оценку, увеличивая её дисперсию и снижая надёжность. Наблюдается, что с увеличением уровня достоверности, доля максимального веса в выборке возрастает — например, от приблизительно 0.056 при α=0.990 до 0.081 при α=0.995. Это свидетельствует об усилении концентрации весов при более высоких уровнях достоверности и может указывать на потенциальную нестабильность оценок, что подчеркивает необходимость применения стратегий для смягчения эффектов концентрации и обеспечения получения стабильных и точных результатов.

Эффективное применение методов, таких как Importance Sampling, требует глубокого понимания взаимосвязи между используемым распределением для выборки и истинным распределением данных. Исследования показывают, что с повышением требуемого уровня достоверности — например, с 0.990 до 0.995 — наблюдается увеличение максимальной доли весов \approx 0.056 до \approx 0.081 . Этот рост свидетельствует о возрастающей концентрации весов в выборке, что может указывать на потенциальную неустойчивость оценок. В условиях высокой концентрации, отдельные элементы выборки оказывают непропорционально большое влияние на результат, что снижает надежность и обобщающую способность модели. Таким образом, анализ зависимости между распределениями и мониторинг концентрации весов являются критически важными для обеспечения точности и стабильности оценок, получаемых с помощью методов Importance Sampling.

Исследование выявило компромисс между вычислительной эффективностью и надежностью методов моделирования. Метод важностной выборки (IS) демонстрирует высокую производительность при корректной спецификации модели, однако его точность существенно снижается при наличии «тяжелых хвостов» в распределении или при неточном описании модели. В таких случаях, метод марковских цепей Монте-Карло с детерминированной выборкой (DMM) обеспечивает более надежные оценки, хотя и с некоторой потерей в вычислительной эффективности и склонностью к консервативным результатам. Таким образом, выбор оптимального метода зависит от конкретной задачи и степени уверенности в адекватности используемой модели.

Повышение уровня достоверности α приводит к снижению эффективного размера выборки (ESS) с приблизительно 154 до 91 и увеличению доли максимального веса с 0.056 до 0.081, что свидетельствует об усилении концентрации весов при более высоких уровнях уверенности.
Повышение уровня достоверности α приводит к снижению эффективного размера выборки (ESS) с приблизительно 154 до 91 и увеличению доли максимального веса с 0.056 до 0.081, что свидетельствует об усилении концентрации весов при более высоких уровнях уверенности.

Расширяя Инструментарий: К Более Реалистичным Моделям Риска

В отличие от широко используемого нормального (Гаусса) распределения, которое предполагает симметричность и отсутствие экстремальных значений, распределение Стьюдента предоставляет более адекватное описание финансовых данных, особенно в условиях рыночных колебаний и возникновения выбросов. t-распределение, благодаря параметру степеней свободы, учитывает возможность появления «толстых хвостов» — повышенной вероятности экстремальных событий, которые часто встречаются на финансовых рынках. Это позволяет более точно моделировать риски, связанные с неожиданными колебаниями цен активов, и создавать более надежные стратегии управления капиталом. Использование распределения Стьюдента позволяет учитывать, что финансовые данные часто не подчиняются строго нормальному закону, что особенно важно при оценке портфельных рисков и разработке моделей ценообразования опционов.

Перспективные исследования в области моделирования рисков направлены на разработку адаптивных стратегий выборки данных. Вместо использования фиксированных методов, эти стратегии способны автоматически корректироваться в зависимости от особенностей анализируемой информации. Идея заключается в том, чтобы алгоритм самостоятельно определял, какие данные наиболее важны для точной оценки риска, и концентрировал усилия именно на них. Например, в периоды повышенной волатильности, алгоритм может увеличить частоту выборки данных, чтобы более оперативно реагировать на изменения рынка. Такой подход позволяет значительно повысить эффективность моделирования, особенно в условиях нестабильной экономической ситуации, и более точно прогнозировать потенциальные убытки, избегая переоценки рисков при наличии выбросов или нетипичных событий.

В условиях растущей сложности финансовых рынков, эффективное управление рисками требует не только усовершенствованных статистических моделей, но и их интеграции с передовыми вычислительными методами. Использование, например, методов Монте-Карло в сочетании с адаптивными алгоритмами сэмплирования и распределенными вычислениями позволяет значительно повысить точность оценки рисков, особенно в случаях, когда традиционные подходы оказываются неэффективными. Такой симбиоз статистического моделирования и вычислительной мощности открывает возможности для анализа сложных финансовых инструментов, стресс-тестирования портфелей в реалистичных сценариях и оперативного реагирования на изменения рыночной конъюнктуры. Разработка и внедрение подобных технологий становится ключевым фактором для обеспечения финансовой стабильности и защиты от непредвиденных убытков в динамично меняющемся мире.

Стандартное отклонение оценки IS уменьшается с увеличением числа степеней свободы ν.
Стандартное отклонение оценки IS уменьшается с увеличением числа степеней свободы ν.

В исследовании, посвящённом оценке рисков и эффективности различных методов, особенно ярко проявляется закономерность, известная, пожалуй, каждому, кто долго работает в сфере разработки. Авторы демонстрируют, что важность корректного моделирования распределения рисков возрастает при отклонении от идеальных условий. Это напоминает о вечной борьбе между эффективностью и надёжностью. Как справедливо заметил Жан-Жак Руссо: «Человек рождается свободным, но повсюду он в цепях». В данном случае, цепи — это упрощения и допущения, необходимые для построения моделей, которые, как только реальность отклоняется от их идеализированного представления, теряют свою точность. Дискретное сопоставление моментов, хоть и менее изящно, чем Importance Sampling, оказывается более устойчивым к этим отклонениям, что не удивительно — всё новое, как правило, просто старое с худшей документацией.

Что дальше?

Представленная работа, как и многие другие, демонстрирует, что эффективность — это иллюзия, а компромисс — вот реальность любой модели. Варианты, превосходящие другие в идеальных условиях, закономерно теряют своё преимущество, когда теория сталкивается с жестокой практикой неверных предположений о хвостах распределений. Упор на дискретное сопоставление моментов, безусловно, добавляет устойчивости, но ценой точности — закономерный обмен, который, вероятно, станет нормой в задачах, где цена ошибки перевешивает стремление к оптимальности.

Впрочем, говорить о решении проблемы не приходится. Скорее, констатируется лишь очередная ступень в бесконечном цикле оптимизации и последующей обратной оптимизации. Всё, что оптимизировано, рано или поздно оптимизируют обратно. Следующим шагом, вероятно, станет поиск более элегантных способов балансировки между эффективностью и робастностью — поиск, который, скорее всего, приведёт к ещё более сложным компромиссам.

Не стоит забывать, что архитектура — это не схема, а компромисс, переживший деплой. В конечном итоге, задача не в создании идеальной модели, а в создании модели, достаточно хорошей для решения конкретной задачи, с пониманием её неизбежных ограничений. Мы не рефакторим код — мы реанимируем надежду.

Оригинал статьи: https://arxiv.org/pdf/2601.09927.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-16 08:21