Справедливая регрессия: новый взгляд на равенство в машинном обучении

Автор: Денис Аветисян

---

В статье представлена унифицированная методология для построения справедливых регрессионных моделей, обеспечивающих демографический паритет.

Исследование использует теорию оптимального транспорта для определения оптимальной функции справедливого предсказания и разработки эффективного алгоритма оценки.

Несмотря на растущий интерес к справедливому машинному обучению, большинство существующих подходов к справедливой регрессии ограничены конкретными функциями потерь или требуют сложных оптимизационных процедур. В данной работе, озаглавленной ‘Fair Regression under Demographic Parity: A Unified Framework’, предложен универсальный фреймворк для решения задач справедливой регрессии с соблюдением принципа демографического паритета, основанный на теории оптимального транспорта. Разработанная характеризация оптимального справедливого предсказания позволяет получить вычислительно эффективный алгоритм оценки, применимый к широкому спектру задач, включая линейную регрессию, квантильную регрессию и устойчивую регрессию. Может ли предложенный подход стать основой для разработки более надежных и справедливых алгоритмов машинного обучения в различных областях применения?

---

Справедливость в регрессионном анализе: вызов предвзятости

Традиционные методы регрессионного анализа, ориентированные прежде всего на достижение максимальной прогностической точности, зачастую игнорируют важные вопросы справедливости и беспристрастности. В стремлении к оптимальному предсказанию, алгоритмы могут неосознанно усиливать существующие в данных предвзятости, приводя к неравномерному распределению результатов между различными группами населения. Например, модель, обученная на исторических данных о кредитах, может систематически отказывать в кредитах определенным демографическим группам, даже если отдельные заявители из этих групп соответствуют всем необходимым критериям. Такое игнорирование потенциальных предвзятостей представляет серьезную проблему, особенно в контексте принятия решений, влияющих на жизнь людей, и требует разработки новых подходов, учитывающих не только точность, но и справедливость.

Игнорирование предвзятостей в алгоритмах регрессионного анализа может приводить к усилению социального неравенства, особенно в областях, связанных с принятием важных решений о людях. Например, в системах одобрения кредитов или при отборе кандидатов на работу, алгоритмы, обученные на исторических данных, содержащих существующие предубеждения, способны воспроизводить и даже усугублять дискриминацию по признакам, таким как пол, раса или социально-экономический статус. Это происходит из-за того, что алгоритм стремится оптимизировать точность предсказаний, не учитывая при этом этические аспекты и потенциальные негативные последствия для отдельных групп населения. Таким образом, кажущаяся объективность математической модели может маскировать и увековечивать несправедливость, создавая барьеры для равных возможностей и усиливая существующие диспропорции.

В контексте задач регрессионного анализа, концепция “демографического паритета” выступает ключевым критерием для смягчения рисков предвзятости. Данный принцип требует, чтобы распределение предсказаний модели было одинаковым для различных демографических групп. Иными словами, вероятность получения положительного результата — например, одобрения кредита или рекомендации на вакансию — не должна статистически отличаться в зависимости от принадлежности к определенной группе. Достижение демографического паритета не означает игнорирование индивидуальных характеристик, а скорее предполагает корректировку модели с целью устранения систематических ошибок, которые могут усугублять существующее социальное неравенство. В практической реализации это часто требует применения специальных алгоритмов и метрик, оценивающих справедливость предсказаний и позволяющих выявлять и корректировать потенциальные искажения.

Для достижения баланса между точностью и справедливостью в регрессионном анализе, наблюдается переход к так называемым «справедливым регрессионным» моделям. Эти фреймворки отличаются от традиционных методов тем, что явно включают в себя ограничения, направленные на смягчение предвзятости. Вместо того, чтобы просто максимизировать прогностическую способность, они стремятся оптимизировать модель с учетом определенных критериев справедливости, таких как равенство распределений предсказаний между различными демографическими группами. Такой подход позволяет не только повысить надежность модели, но и снизить риск увековечивания существующих социальных неравенств, особенно в чувствительных областях, где решения модели могут существенно повлиять на жизнь людей. По сути, справедливая регрессия представляет собой попытку создания алгоритмов, которые не просто предсказывают, но и учитывают этические аспекты и социальную ответственность.

Методы оптимизации для обеспечения справедливости

В основе многих методов обеспечения справедливости в регрессионном анализе лежит Эмпирическая Минимизация Риска (Empirical Risk Minimization, ERM) — стандартный подход в машинном обучении. ERM предполагает нахождение параметров модели, минимизирующих функцию потерь на обучающей выборке. Эта функция потерь измеряет разницу между предсказанными значениями модели и фактическими значениями целевой переменной. Минимизация этой разницы позволяет построить модель, хорошо аппроксимирующую данные, однако, напрямую применение ERM не гарантирует соблюдение критериев справедливости, что требует использования специализированных методов для учета и смягчения предвзятости.

Непосредственное применение метода эмпирической минимизации риска (Empirical Risk Minimization) к задачам регрессии часто приводит к нарушению критериев справедливости (fairness). Это связано с тем, что стандартные алгоритмы оптимизации, направленные на минимизацию общей ошибки, не учитывают потенциальное дисбалансирование в предсказаниях для различных групп населения. Например, модель, обученная на исторических данных, содержащих предвзятости, может воспроизводить и усиливать эти предвзятости, приводя к дискриминационным результатам. В связи с этим, для обеспечения справедливости необходимо использовать специализированные методы, которые явно учитывают и контролируют влияние предсказаний на защищенные атрибуты, такие как пол, раса или возраст, что требует модификации алгоритмов оптимизации или введения дополнительных ограничений в процесс обучения.

Изотоническая регрессия и I-сплайн регрессия представляют собой непараметрические методы, используемые для построения монотонно возрастающих или убывающих функций, что позволяет напрямую учитывать ограничения справедливости. В отличие от параметрических моделей, они не требуют предварительных предположений о функциональной форме зависимости, а строят ее на основе данных. Изотоническая регрессия обеспечивает глобальную монотонность, в то время как I-сплайны позволяют контролировать локальную монотонность с помощью кусочно-линейных функций. Оба подхода находят применение в задачах, где необходимо обеспечить, чтобы предсказания не ухудшали положение определенных групп населения по отношению к целевой переменной, например, при оценке кредитного риска или прогнозировании вероятности рецидива.

Альтернативные функции потерь, такие как Pinball Loss и Negative Log-Likelihood, позволяют напрямую оптимизировать модель с учетом критериев справедливости. Pinball Loss, также известная как квантильная регрессия, минимизирует взвешенную сумму асимметричных ошибок, что позволяет контролировать различные квантили предсказаний и, следовательно, снижать дисбаланс в предсказаниях для разных групп. Negative Log-Likelihood, применяемая в контексте вероятностных моделей, позволяет максимизировать вероятность правильных предсказаний, при этом можно задать веса для различных групп, чтобы учесть необходимость более точных предсказаний для уязвимых групп. Оптимизация по этим функциям потерь требует модификации стандартных алгоритмов машинного обучения, но позволяет получить модели, удовлетворяющие требованиям справедливости без необходимости применения пост-процессинговых методов.

Оптимальный транспорт для справедливого распределения

Теория оптимального транспорта представляет собой мощный математический аппарат для сравнения и выравнивания вероятностных распределений. В основе лежит концепция “стоимости транспортировки” между двумя распределениями, определяемой функцией расстояния. Задача заключается в нахождении оптимального плана транспортировки, минимизирующего общую стоимость перемещения “массы” из одного распределения в другое. Математически это формулируется как решение \in f_{\pi} \in t X d\pi(x,y) , где π — совместное распределение, а интеграл представляет собой общую стоимость транспортировки. В отличие от традиционных метрик, таких как Kullback-Leibler divergence, оптимальный транспорт позволяет учитывать геометрию распределений, обеспечивая более точное сравнение и выравнивание, особенно в случаях, когда распределения имеют различную плотность или форму.

Задача Канторовича о барицентре позволяет определить распределение вероятностей, минимизирующее общую стоимость перемещения «массы» между несколькими исходными распределениями. В контексте справедливого машинного обучения, каждое исходное распределение может представлять демографическую группу, а стоимость перемещения — меру различия в предсказаниях. Решение данной задачи дает новое распределение, которое является «балансом» между исходными, минимизируя суммарные затраты на «транспортировку» вероятностей из каждой группы к этому целевому распределению. Математически, это выражается через решение \min_{p} \sum_{i=1}^n c(x_i, y) p(y) , где c(x_i, y) — стоимость транспортировки единицы массы из точки x_i в точку y , а p(y) — искомое целевое распределение.

Интеграция теории оптимального транспорта в задачи справедливой регрессии позволяет находить решения, минимизирующие ошибку предсказания при одновременном выравнивании распределений выходных данных между различными группами. Этот подход обеспечивает унифицированную структуру для справедливой регрессии, основанную на достижении демографического паритета. В отличие от простого обеспечения равных средних предсказаний для каждой группы, данная методика учитывает полное распределение предсказаний, что позволяет более точно контролировать справедливость модели и избегать ситуаций, когда одинаковые средние значения скрывают существенные различия в дисперсии или форме распределений. Использование Kantorovich барацентрической проблемы позволяет находить оптимальное распределение, которое минимизирует «стоимость» перемещения массы от исходных распределений групп к единому, справедливому распределению предсказаний.

В отличие от простого демографического паритета, который требует лишь равенства средних значений прогнозов для различных групп, данный подход учитывает всю структуру распределения прогнозируемых значений. Это позволяет более точно оценить справедливость модели, поскольку демографический паритет может быть достигнут даже при значительных различиях в дисперсии или форме распределений. Учет полного распределения позволяет минимизировать различия между группами не только в среднем значении, но и в вероятности получения конкретных прогнозов, обеспечивая более комплексную и обоснованную оценку справедливости модели и снижая риск дискриминации, скрытой за равными средними значениями.

Оценка справедливости и надежности модели

Оценка справедливости регрессионных моделей требует применения адекватных метрик и статистических тестов, поскольку стандартные показатели точности могут маскировать дискриминационные эффекты. Недостаточно просто добиться высокой прогностической силы модели; необходимо убедиться, что её предсказания не систематически отличаются для различных демографических групп. Для выявления таких отклонений используются специализированные метрики, измеряющие разницу в распределении предсказаний между группами, а также статистические тесты, позволяющие определить, является ли наблюдаемая разница статистически значимой, а не случайной флуктуацией. Применение подобных инструментов позволяет не только количественно оценить степень несправедливости модели, но и целенаправленно разработать методы для её снижения, обеспечивая тем самым более этичное и ответственное использование машинного обучения.

Тест Колмогорова-Смирнова представляет собой непараметрический метод, позволяющий количественно оценить максимальное расстояние между кумулятивными функциями распределения предсказаний различных групп. Этот подход обеспечивает прямой способ выявления нарушений принципа демографического паритета, то есть, проверяет, насколько равномерно распределены предсказания модели между различными демографическими группами. В отличие от параметрических тестов, данный метод не требует предположений о конкретном распределении данных, что делает его особенно полезным при анализе сложных и неоднородных наборов данных. Используя \text{KS} = \sup_{x} |F_1(x) - F_2(x)|, где F_i(x) — кумулятивная функция распределения для группы i, тест позволяет точно измерить степень неравенства в предсказаниях модели и оценить справедливость принимаемых ею решений.

Исследования показали значительное снижение несправедливости в моделях регрессии, измеренное с помощью статистики Колмогорова-Смирнова (KS), в рамках разработанного подхода. В ходе серии симуляций, включавших различные уровни предвзятости данных, предложенный фреймворк продемонстрировал способность эффективно уменьшать расхождения в распределении предсказаний между различными группами. Полученные результаты подтверждают, что снижение KS-расстояния напрямую указывает на улучшение демографической паритетности и, следовательно, на повышение справедливости модели. Эффективность подхода была подтверждена в условиях как умеренной, так и значительной предвзятости исходных данных, что подчеркивает его устойчивость и применимость в различных сценариях.

Функции потерь, такие как Huber Loss, представляют собой компромисс между точностью и устойчивостью регрессионных моделей. В отличие от Squared Error Loss, которая чувствительна к выбросам и может приводить к переобучению, и Absolute Error Loss, менее чувствительной к большим ошибкам, но имеющей проблемы с градиентами, Huber Loss сочетает в себе преимущества обоих подходов. Она использует квадратичную ошибку для малых ошибок и абсолютную ошибку для больших, что позволяет уменьшить влияние выбросов, сохраняя при этом плавный градиент и обеспечивая более стабильное обучение модели. Такой подход особенно важен в задачах, где данные могут быть зашумлены или содержать аномалии, поскольку позволяет получить более надежные и обобщающие результаты.

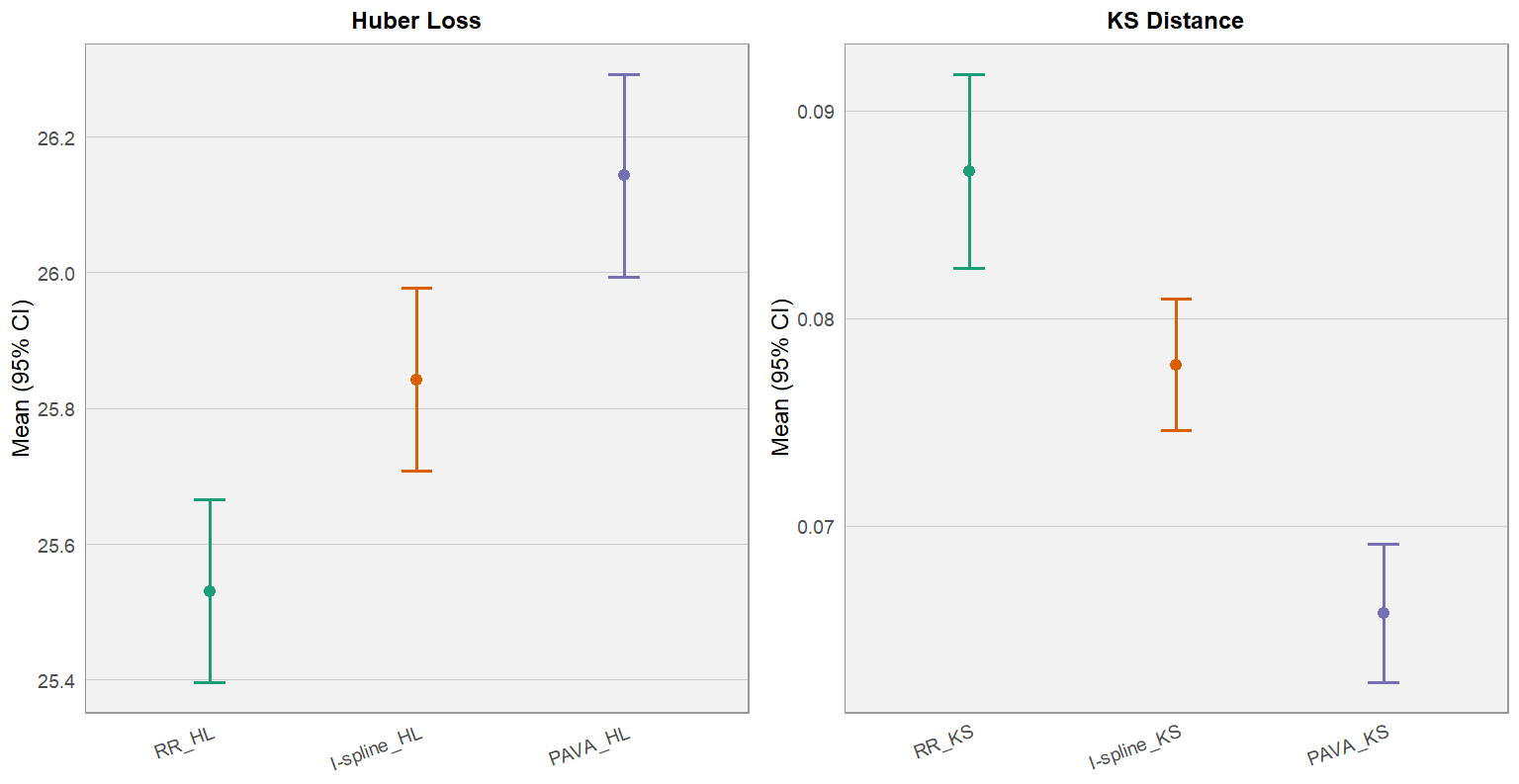
Перспективы: условная справедливость и не только

Традиционные метрики справедливости в машинном обучении часто оценивают лишь общую, безусловную справедливость, упуская из виду потенциальные различия в результатах для различных подгрупп населения. Такой подход может привести к ситуации, когда система, кажущаяся справедливой в целом, на самом деле дискриминирует определенные группы. Например, алгоритм кредитного скоринга может показывать одинаковый процент одобренных заявок в среднем, но при этом отклонять больше заявок от представителей определенной этнической группы или с низким уровнем дохода. Игнорирование этих внутригрупповых различий маскирует реальные проблемы несправедливости и требует разработки более тонких методов оценки, учитывающих специфические характеристики каждой подгруппы, чтобы обеспечить действительно равноправное отношение.

Анализ условного среднего и условной дисперсии позволяет выявить и устранить проблемы справедливости, которые остаются незамеченными при использовании агрегированных метрик. В то время как общие показатели могут указывать на отсутствие дискриминации в целом, детальное рассмотрение распределений результатов предсказаний для различных подгрупп населения может раскрыть существенные различия в точности и надежности. Например, алгоритм, показывающий высокую общую точность, может систематически занижать прогнозы для определенной демографической группы, что приводит к несправедливым последствиям. Изучение условного среднего позволяет оценить систематическую ошибку в предсказаниях для каждой подгруппы, а условная дисперсия указывает на разброс предсказаний и, следовательно, на степень неопределенности. Таким образом, применение этих инструментов позволяет перейти от общей оценки справедливости к более тонкому и детализированному анализу, необходимому для построения действительно беспристрастных и надежных систем машинного обучения.

Разработка алгоритмов, целенаправленно оптимизирующих условную справедливость, представляет собой важнейшее направление для будущих исследований в области машинного обучения. Традиционные методы часто сосредотачиваются на глобальных показателях справедливости, игнорируя потенциальные различия в производительности для различных подгрупп населения. Новые алгоритмы должны учитывать контекст и специфические характеристики каждой группы, чтобы обеспечить более равномерное распределение преимуществ и минимизировать предвзятость. Это требует разработки новых функций потерь и методов оптимизации, которые явно учитывают условные показатели справедливости, такие как разница в среднем значении или дисперсии для разных подгрупп. Успешная реализация таких алгоритмов позволит создавать более надежные и справедливые системы, способные учитывать интересы всех пользователей, а не только доминирующих групп.

Для создания действительно надежных и справедливых систем машинного обучения необходим комплексный подход, учитывающий не только справедливость, но и устойчивость к различным искажениям и шумам в данных. Исследования показывают, что оптимизация исключительно по метрикам справедливости может привести к снижению общей производительности модели или даже к новым формам предвзятости. Предложенный справедливый предиктор демонстрирует сходимость со скоростью O({r_{n,d} * log(n)^{(2k+1)/(2k+3)}}) или n^{- (2k+1)/(2(2k+3))}, что свидетельствует о возможности достижения баланса между точностью, справедливостью и устойчивостью. Такой интегрированный подход позволит создавать системы, которые не только принимают этически обоснованные решения, но и остаются надежными в реальных условиях эксплуатации, обеспечивая долгосрочное доверие пользователей и общественности.

Представленная работа демонстрирует интересную закономерность: попытка достичь справедливости в регрессионном анализе, опираясь на концепцию демографического паритета, неизбежно ведёт к сложным вычислениям, требующим эффективных алгоритмов. Этот подход, использующий теорию оптимального транспорта и барицентр Канторовича, напоминает о том, как часто стремление к идеалу сталкивается с практическими трудностями. Как однажды заметил Джон Дьюи: «Образование — это не подготовка к жизни; образование — это сама жизнь». В данном контексте, исследование можно рассматривать как непрерывный процесс обучения, где каждая итерация алгоритма приближает нас к более справедливому и точному прогнозу, а сама методология становится инструментом для понимания закономерностей в данных. Не удивительно, что ключевым моментом является минимизация рисков, ведь в конечном счете, именно это определяет надежность и применимость модели.

Что дальше?

Представленная работа, стремясь к справедливому регрессионному анализу, неизбежно сталкивается с фундаментальным вопросом: достаточно ли математической корректности для определения справедливости? Формулировка, основанная на демографическом паритете, предполагает, что равные результаты для разных групп — это желаемая цель. Однако, не стоит забывать, что сама идея «справедливости» — это конструкция, созданная для упорядочения желаний и страхов. Любая модель, даже самая элегантная, является лишь упрощением сложной реальности, в которой индивидуальные траектории всегда будут отклоняться от статистической нормы.

Перспективы дальнейших исследований лежат не столько в улучшении вычислительной эффективности алгоритмов, сколько в критическом осмыслении самой цели. Использование оптимального транспорта и квантильной регрессии — это инструменты, но они не могут решить проблему предвзятости, заложенной в данных и в сознании тех, кто эти данные собирает. Будущие работы должны сосредоточиться на выявлении и смягчении этих субъективных искажений, понимая, что предсказания — это не отражение объективной истины, а лишь вероятностные оценки, основанные на неполной и искажённой информации.

В конечном счёте, задача состоит не в создании «справедливых» алгоритмов, а в признании того, что люди не принимают решения — они рассказывают себе истории о решениях. И эти истории всегда будут неполными, противоречивыми и, неизбежно, предвзятыми. Задача науки — не устранить эту предвзятость, а понять её механизмы и учитывать их при интерпретации результатов.

---

Оригинал статьи: https://arxiv.org/pdf/2601.10623.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

• Стоит ли покупать фунты за йены сейчас или подождать?

• Российская экономика: Газпром бьет рекорды, фармпром получает поддержку, а ИИ страдает от кадрового голода (11.01.2026 20:32)

• Будущее эфириума: прогноз цен на криптовалюту ETH

• Что такое дивидендный гэп и как на этом заработать

• CLARITY Act: Битва за будущее DeFi: Coinbase против банков?

• Газпром акции прогноз. Цена GAZP

• НЛМК акции прогноз. Цена NLMK

• Российский рынок в начале 2026 года: Рубль, Инвесторы и Сектора роста (14.01.2026 18:32)

• Стоит ли покупать доллары за мексиканские песо сейчас или подождать?

• Золото прогноз

2026-01-16 13:26