Стратегические игры: как предсказать поведение в условиях неопределенности

Автор: Денис Аветисян

Новое исследование предлагает методы машинного обучения для анализа стратегических взаимодействий и моделирования поведения агентов в различных сценариях.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал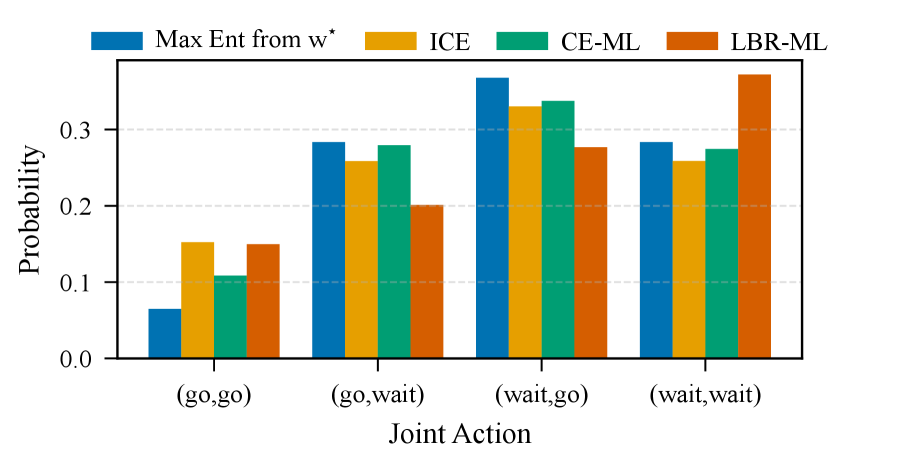

Вероятностное распределение равновесий по совместным действиям, рассчитанное для временного горизонта в 2000 единиц, демонстрирует закономерности формирования стабильных состояний в динамической системе.

Представлены два алгоритма обратного обучения в $2 imes2$ играх, CE-ML и LBR-ML, для оценки полезности агентов и моделирования стратегических взаимодействий, демонстрирующие различные преимущества в скоординированных и нескоординированных условиях.

Понимание стратегий взаимодействия агентов по ограниченным данным поведения остается сложной задачей в моделировании многоагентных систем. В настоящей работе, ‘Inverse Learning in $2\times2$ Games: From Synthetic Interactions to Traffic Simulation’, предложены два подхода к обратному обучению в рамках теории игр: CE-ML и LBR-ML, позволяющие оценить полезность действий агентов и моделировать их стратегическое взаимодействие. Полученные результаты демонстрируют, что CE-ML эффективен в координационных сценариях, в то время как LBR-ML обеспечивает большую устойчивость в условиях отсутствия координации. Смогут ли предложенные методы найти применение в более сложных моделях поведения и оптимизации транспортных потоков?

Равновесие в Действии: Стратегическое Взаимодействие и Его Моделирование

Множество реальных процессов, от экономических взаимодействий до организации дорожного движения, успешно моделируются как стратегические взаимодействия между отдельными агентами. В этих системах каждый участник принимает решения, учитывая возможные действия других, стремясь максимизировать собственный результат. Например, при ценообразовании компании учитывают стратегии конкурентов, а в транспортных потоках каждый водитель выбирает маршрут и скорость, влияя на общую пропускную способность. Такой подход позволяет анализировать сложные системы, выявлять закономерности и прогнозировать поведение, что важно для разработки эффективных стратегий и оптимизации процессов в различных областях, включая экономику, политику и даже биологию.

Равновесие Нэша представляет собой краеугольный камень анализа стратегических взаимодействий. Оно описывает состояние, в котором каждый участник процесса выбрал такую стратегию, что, учитывая стратегии остальных, ни у кого нет стимула изменить свой выбор в одностороннем порядке. Иными словами, если все остальные игроки придерживаются своих стратегий, отклонение от выбранной стратегии не принесет выгоды ни одному из участников. $\text{max}_{s_i} u_i(s_i, s_{-i})$ — эта формула демонстрирует, что игрок $i$ максимизирует свою выгоду, учитывая стратегии других игроков $s_{-i}$ . Данное понятие является фундаментальным для понимания стабильности в различных областях, включая экономику, теорию игр и даже эволюционную биологию, позволяя прогнозировать и анализировать поведение рациональных агентов в конкурентной среде.

В отличие от равновесия Нэша, которое предполагает отсутствие стимулов для одностороннего отклонения при полной неопределенности, концепция коррелированного равновесия учитывает возможность обмена информацией между игроками. Это позволяет достигать более эффективных исходов, поскольку игроки могут координировать свои действия на основе общей информации или сигнала. Представьте ситуацию, где два водителя приближаются к перекрестку: при равновесии Нэша оба могут попытаться проехать первыми, что приводит к аварии. Однако, если они заранее договорились, кто проедет первым (например, по четным/нечетным числам в номере автомобиля), и придерживаются этого соглашения, они избегают столкновения и достигают более благоприятного результата. Таким образом, коррелированное равновесие демонстрирует, что обмен информацией и координация действий могут существенно улучшить исход стратегического взаимодействия, расширяя возможности анализа и моделирования реальных ситуаций, где информация не всегда ограничена.

Распределение равновесий по совместным действиям при [latex]T=500[/latex] демонстрирует вероятностную природу стабильных состояний системы. — Распределение равновесий по совместным действиям при $T=500$ демонстрирует вероятностную природу стабильных состояний системы.

Обратное Моделирование: Раскрытие Стратегий через Наблюдение

Обратное игровое моделирование (Inverse Game-Theoretic Learning) представляет собой набор инструментов, предназначенных для вывода полезности и стратегий агентов на основе наблюдения за их действиями. Этот подход позволяет реконструировать скрытые предпочтения и модели принятия решений, анализируя наблюдаемое поведение. В отличие от традиционного игрового моделирования, где стратегии и полезности задаются априори, обратное моделирование использует наблюдаемые действия как входные данные для оценки этих параметров. Метод применим в различных областях, включая экономику, социологию и искусственный интеллект, где необходимо понимать мотивации и стратегии действующих субъектов на основе имеющихся данных об их поведении.

Метод обратного игрового обучения использует принципы как равновесия Нэша, так и коррелированного равновесия для вывода полезностей и стратегий агентов. Разработанные нами формулировки CE-ML и LBR-ML демонстрируют значительные преимущества в точности по сравнению с существующими подходами. CE-ML, в частности, показывает более низкие значения среднеквадратичной ошибки (RMSE) в ходе экспериментов, что указывает на повышенную эффективность оценки параметров, в то время как LBR-ML обеспечивает устойчивость к неполной информации и динамическим изменениям в поведении агентов. $RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y}_i)^2}$ является основной метрикой оценки точности.

Динамика логит-ответов (Logit Best Response Dynamics) представляет собой реалистичную модель, описывающую процесс обучения и адаптации стратегий агентов во времени. В отличие от предположений о мгновенной оптимизации, данная модель учитывает, что агенты совершают ошибки и выбирают стратегии с вероятностью, зависящей от их ожидаемой выгоды, что соответствует наблюдаемому поведению в реальных сценариях. Экспериментальные данные демонстрируют, что алгоритм CE-ML, использующий данную динамику, последовательно достигает более низких значений среднеквадратичной ошибки (RMSE) по сравнению с альтернативными подходами, что свидетельствует о повышении точности оценки параметров полезности агентов и, следовательно, о более надежном выводе их намерений.

Дорожное Движение как Стратегическая Игра: Моделирование и Анализ

Симулятор дорожного движения SUMO предоставляет высокодетализированную микроскопическую среду для моделирования взаимодействия транспортных средств и потока трафика. В отличие от макроскопических моделей, SUMO позволяет отслеживать перемещение каждого отдельного автомобиля, учитывая его скорость, положение, тип и поведение водителя. Это достигается за счет эмуляции физических параметров, таких как ускорение, торможение и смену полосы движения, а также учета правил дорожного движения и инфраструктуры. Такой подход позволяет исследовать влияние отдельных решений водителей на общую картину трафика, а также тестировать различные стратегии управления транспортными потоками, включая адаптивные системы управления и интеллектуальные транспортные системы.

В рамках моделирования дорожного движения в SUMO, взаимодействие между транспортными средствами может быть представлено как игры в нормальной форме 2×2. В данном контексте, каждое транспортное средство рассматривается как игрок, а доступные действия — например, смена полосы движения или изменение скорости — формируют стратегический набор. Такое представление позволяет формализовать процесс принятия решений каждым водителем, учитывая возможные действия других участников движения и их потенциальное влияние на результат. В частности, каждое действие водителя можно рассматривать как выбор стратегии в матрице выплат, определяющей ожидаемую выгоду (например, сокращение времени в пути или повышение безопасности) в зависимости от комбинации стратегий, выбранных всеми участниками взаимодействия.

Применение обратного игрового обучения (Inverse Game-Theoretic Learning) к данным моделирования трафика в SUMO позволяет с высокой точностью выводить предпочтения и стратегическое поведение водителей. В частности, алгоритм LBR-ML демонстрирует 72.6% точность предсказания совместных действий в неорганизованных сценариях (Эксперимент E4), что подтверждает его устойчивость. Параметры рациональности (λ1, λ2) варьируются в диапазоне от 1.0 до 3.0, что указывает на способность водителей адаптировать свое поведение в отсутствие координации с другими участниками движения.

Исследование демонстрирует, что понимание стратегических взаимодействий требует не только предсказания поведения, но и реконструкции лежащих в его основе мотивов. Авторы предлагают два подхода — CE-ML и LBR-ML — для оценки полезности агентов, подчеркивая, что выбор метода зависит от степени координации в системе. Это согласуется с мыслью Роберта Тарьяна: «Программное обеспечение подобно ледяному айсбергу: видимая часть — это лишь малая доля того, что скрыто под поверхностью». Подобно тому, как анализ программного кода требует проникновения в скрытые слои, так и моделирование взаимодействий требует выявления скрытых предпочтений и стратегий, определяющих поведение участников. CE-ML, преуспевающий в координации, и LBR-ML, устойчивый в условиях разобщенности, демонстрируют, что понимание системы открывает путь к её моделированию и предсказанию.

Что дальше?

Представленные рамки CE-ML и LBR-ML — лишь отправная точка. Что произойдёт, если отказаться от предположения о рациональности игроков? Если допустить, что «логит-ответ» — это не приближение к оптимальной стратегии, а фундаментальное свойство принятия решений, обусловленное когнитивными ограничениями? Тогда моделирование станет не поиском «истинных» предпочтений, а реконструкцией искажённой картины мира, где шум и неточность — это норма. Отказ от поиска «истинной» рациональности может привести к более реалистичным, хотя и менее предсказуемым моделям.

Особый интерес представляет вопрос о масштабируемости. Смогут ли эти методы справиться с играми, где число игроков и стратегий растёт экспоненциально? Предположение о коррелированном равновесии — элегантное решение, но его вычислительная сложность может стать непреодолимым препятствием. Возможно, стоит обратить внимание на приближённые алгоритмы и методы снижения размерности, даже если это потребует некоторой потери точности. Что если «достаточно хорошее» решение лучше, чем «идеальное», но недостижимое?

И, наконец, вопрос о границах применимости. Трафик — лишь одна из возможных областей применения. Смогут ли эти методы быть адаптированы для моделирования экономических рынков, политических взаимодействий или даже эволюции видов? Отказ от универсальности и признание специфики каждой системы может стать ключом к созданию действительно полезных моделей. В конце концов, реальность сложнее любой абстракции.

Оригинал статьи: https://arxiv.org/pdf/2601.10367.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-16 19:59