Сглаживание будущего: Как непрерывные временные ряды открывают новые горизонты в AI

Автор: Денис Аветисян

Новый подход к токенизации финансовых данных позволяет извлекать более глубокие закономерности и повышать эффективность алгоритмов принятия решений.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал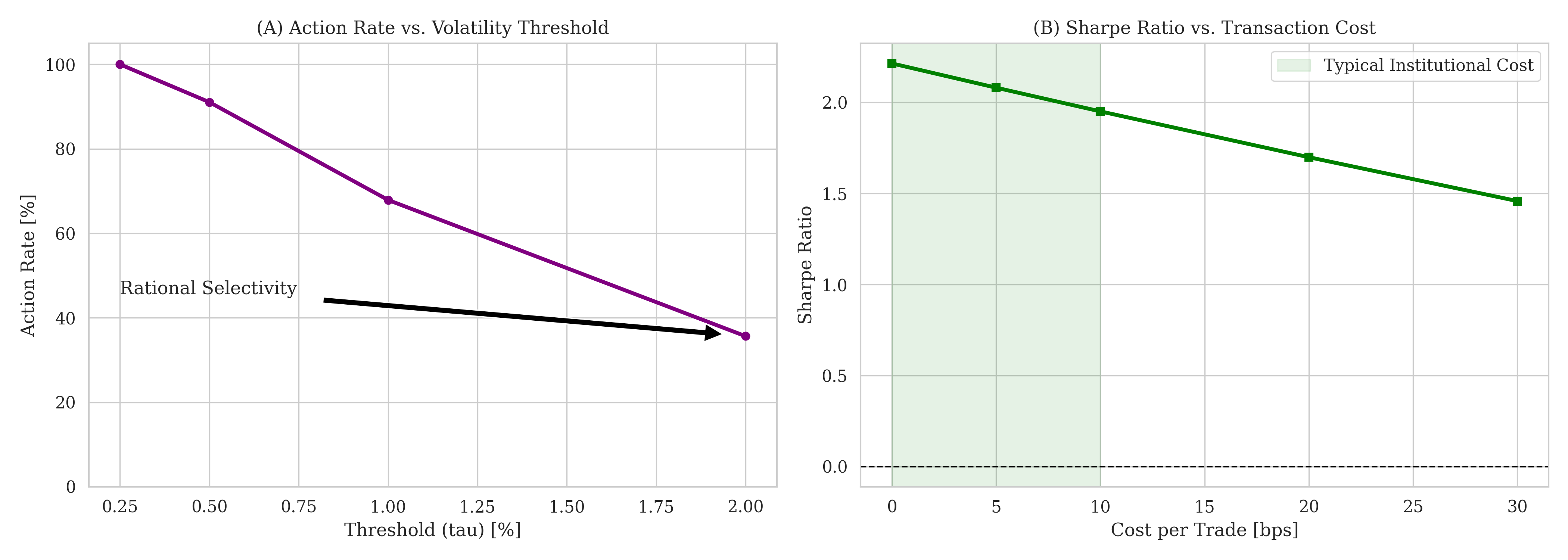

При анализе чувствительности параметров системы NVDA выяснилось, что SplineGPT демонстрирует рациональную избирательность: с увеличением порога волатильности τ (усложнением задачи) частота действий модели монотонно снижается, что позволяет избежать ложных срабатываний, при этом сохраняя устойчивую производительность (коэффициент Шарпа > 2.0) даже в условиях высокого трения (до 30 базисных пунктов), подтверждая, что альфа, генерируемая кинематическими токенами, не является лишь арбитражем микроструктуры.

В статье представлена модель SplineGPT, использующая сплайн-токенизацию для анализа временных рядов и оптимизации стратегий управления рисками.

Дискретные представления данных часто оказываются хрупкими при работе с зашумленными временными рядами, особенно в условиях асимметричных потерь, стимулирующих отказ от действий. В данной работе, ‘Kinematic Tokenization: Optimization-Based Continuous-Time Tokens for Learnable Decision Policies in Noisy Time Series’, предложен подход Kinematic Tokenization, основанный на оптимизации и использующий непрерывные сплайн-токены для извлечения кинематических признаков высокого порядка. Эксперименты на финансовых данных показали, что такой подход позволяет создавать стабильные и откалиброванные стратегии, в отличие от дискретных методов, склонных к “выходу на кассу”. Сможет ли непрерывная токенизация временных рядов открыть новые горизонты в обучении эффективных и надежных систем принятия решений в условиях неопределенности?

За пределами дискретных временных рядов: Непрерывное представление как необходимость

Традиционные методы анализа временных рядов, основанные на дискретном представлении времени, зачастую приводят к потере ценной информации и снижению прогностической силы моделей. При переходе от непрерывного сигнала к дискретному, происходит квантование, в результате которого теряются детали, важные для точного описания динамики процесса. Это особенно критично для сигналов с высокой частотой изменений или нерегулярными интервалами, где дискретизация может исказить реальную картину и привести к ошибкам прогнозирования. Например, в финансовых рынках или нейрофизиологических исследованиях, где даже малейшие изменения могут иметь значительные последствия, потеря информации из-за дискретизации может существенно повлиять на точность моделей и их способность предсказывать будущие события. Таким образом, использование дискретных представлений времени создает ограничения для анализа и моделирования реальных процессов, подчеркивая необходимость разработки методов, способных эффективно работать с непрерывными сигналами.

Реальные сигналы, будь то колебания на финансовых рынках, изменения климата или физиологические процессы, по своей природе непрерывны. Игнорирование этой непрерывности в традиционных методах анализа временных рядов, основанных на дискретных измерениях, неизбежно приводит к потере информации и снижению точности прогнозов. Представление сигнала в дискретном виде — это всегда приближение, которое может упустить важные нюансы и взаимосвязи, особенно в случаях, когда изменения происходят быстро или нерегулярно. Точное моделирование и предсказание требует учитывать весь спектр изменений сигнала, а не только отдельные моменты времени, что делает разработку методов для работы с непрерывными сигналами критически важной задачей для повышения эффективности анализа данных и улучшения качества прогнозов в самых разных областях науки и техники.

Существующие методы анализа временных рядов зачастую оказываются недостаточно эффективными при работе с непрерывными сигналами, что приводит к снижению точности прогнозов и выявлению закономерностей. Традиционные подходы, дискретизируя поток данных, неизбежно теряют ценную информацию о моментальных изменениях и тонких взаимосвязях, существующих между последовательными точками. Это особенно критично в областях, где важна высокая точность и оперативность, например, в финансовых прогнозах, мониторинге состояния оборудования или обработке медицинских данных. Неспособность адекватно представлять и обрабатывать непрерывные сигналы создает заметный пробел в производительности, стимулируя поиск новых, более совершенных методов, способных учитывать динамику процессов в реальном времени и обеспечивать более надежные результаты.

Оптимизация сплайнами и обогащение данных: Путь к непрерывности

Оптимизация сплайнами представляет собой эффективный метод аппроксимации непрерывных функций на основе дискретных данных. В отличие от полиномиальной интерполяции, сплайны используют кусочно-полиномиальные функции, обеспечивая более гладкое и стабильное приближение, особенно при большом количестве данных. Используя узлы (дискретные точки данных) и задавая условия гладкости в этих точках, можно построить сплайн, который минимизирует погрешность аппроксимации. Существуют различные типы сплайнов, такие как кубические сплайны, которые часто используются благодаря их способности точно воспроизводить исходные данные и обеспечивать хорошую сходимость. Этот метод позволяет эффективно реконструировать непрерывную функцию из ограниченного набора дискретных измерений, что критически важно для анализа и моделирования данных во многих областях, включая обработку сигналов и машинное обучение.

Комбинирование сплайн-оптимизации с обогащением данных на основе оптимизации позволяет получить более точное и полное представление исходных данных. Сплайн-оптимизация эффективно аппроксимирует непрерывные функции по дискретным точкам, а обогащение данных, основанное на оптимизации, добавляет информацию, повышая детализацию и уменьшая шум. Данный подход позволяет создавать более качественные модели, поскольку он учитывает не только имеющиеся данные, но и оптимизированные значения, полученные в процессе обогащения, что приводит к повышению точности прогнозов и снижению погрешности модели. Эффективность метода заключается в совместном использовании гладкости сплайнов и информативности обогащенных данных.

В рамках оптимизации непрерывных сигналов, логарифмическое преобразование данных эффективно используется для сужения диапазонов значений и стабилизации дисперсии. Применение логарифма $log(x)$ к данным позволяет уменьшить влияние выбросов и привести данные к более нормальному распределению, особенно в случаях, когда исходные данные имеют экспоненциальный рост или широкий динамический диапазон. Это особенно полезно для временных рядов, где стабилизация дисперсии является важным условием для корректной работы многих моделей прогнозирования и анализа, включая модели, чувствительные к гетероскедастичности. Такой подход позволяет улучшить точность и надежность результатов анализа данных.

Предварительная обработка данных с использованием сплайнов и обогащения позволяет повысить эффективность работы продвинутых моделей временных рядов. Оптимизация и преобразование дискретных данных в непрерывное представление, а также нормализация диапазонов значений и стабилизация дисперсии, улучшают качество входных данных для алгоритмов прогнозирования. Это, в свою очередь, приводит к более точным и надежным результатам моделирования, особенно при работе с данными, содержащими шум или пропуски. Подготовленные данные облегчают выявление закономерностей и трендов, что критически важно для долгосрочного прогнозирования и анализа временных рядов.

Стратегия SplineGPT, использующая управление активными рисками, демонстрирует сглаживание волатильности (например, для TSLA) и сохранение капитала во время обвала PFE (красная линия), в отличие от стратегии Buy & Hold, при этом базовые модели показали сходимость к ликвидационному равновесию, выраженному в постоянной продаже активов (см. таблицы 5, 6 и 7).

Модели пространства состояний и селективное сканирование: Новые горизонты анализа временных рядов

Модели пространства состояний (SSM) представляют собой мощный инструмент для моделирования последовательных данных, основываясь на представлении скрытого состояния системы. В отличие от прямого анализа входных данных, SSM используют внутреннее, латентное представление — вектор состояния — которое обновляется с каждым новым элементом последовательности. Это позволяет модели улавливать зависимости и контекст в данных, сохраняя информацию о прошлом для прогнозирования будущего. Математически, SSM описываются уравнениями, связывающими текущее состояние с предыдущим и текущим входом, а также выходные данные с текущим состоянием. $x_{t+1} = Ax_t + Bu_t$ и $y_t = Cx_t + Du_t$ — типичные примеры таких уравнений, где $x_t$ — состояние, $u_t$ — вход, а $y_t$ — выход на шаге времени t. Вместо обработки всей последовательности сразу, SSM обрабатывают её поэтапно, обновляя состояние с каждым новым элементом, что делает их эффективными для работы с длинными последовательностями.

Модели, такие как Mamba, используют механизмы селективного сканирования (selective scan) в рамках моделей пространства состояний (SSM) для повышения эффективности и точности обработки последовательностей. В отличие от традиционных SSM, применяющих сканирование ко всей последовательности, селективное сканирование динамически определяет, какие части последовательности наиболее релевантны для текущего состояния и фокусируется именно на них. Это достигается путем вычисления весов важности для каждого элемента последовательности на основе текущего состояния и контекста, что позволяет модели игнорировать несущественную информацию и концентрироваться на ключевых данных. Такой подход существенно снижает вычислительные затраты и позволяет обрабатывать более длинные последовательности с большей точностью, особенно в задачах, где релевантная информация распределена неравномерно.

Жидкостные нейронные сети (ЖНС), основанные на моделях пространства состояний (SSM), моделируют активацию нейронов посредством дифференциальных уравнений, что позволяет имитировать динамику биологических нейронных сетей. В отличие от традиционных искусственных нейронных сетей, где активации вычисляются дискретно, ЖНС используют непрерывные во времени уравнения для описания изменения состояния нейронов. Эти уравнения, как правило, описывают взаимосвязи между входными сигналами, внутренним состоянием нейрона и выходным сигналом, позволяя моделировать временную динамику и адаптацию нейронов. Такой подход позволяет ЖНС более эффективно обрабатывать временные ряды и последовательности данных, а также потенциально обеспечивает более высокую устойчивость и адаптивность по сравнению с дискретными моделями.

В задачах моделирования длинных последовательностей, таких как обработка естественного языка и анализ временных рядов, методы на основе моделей пространства состояний (SSM), включая Mamba и Liquid Neural Networks, демонстрируют превосходство над традиционными рекуррентными (RNN) и трансформаторными (Transformer) архитектурами. Это обусловлено способностью SSM эффективно обрабатывать долгосрочные зависимости и избегать проблем затухания или взрыва градиентов, характерных для RNN, а также снижением вычислительной сложности по сравнению с механизмами внимания в Transformer, особенно при обработке очень длинных последовательностей. Экспериментальные результаты показывают, что SSM достигают более высокой точности и требуют меньше вычислительных ресурсов для задач, где важна обработка больших объемов последовательных данных.

В отличие от базовой модели PatchTST, демонстрирующей тенденцию к выбору одного действия, SplineGPT поддерживает широкое распределение действий и обеспечивает четкое разграничение между состояниями удержания и совершения сделок, при этом его вероятностные оценки для сигналов «Купить» соответствуют фактической прибыльности.

Масштабирование для больших наблюдений: Эффективное обучение и адаптация

В современных приложениях анализа временных рядов, таких как прогнозирование нагрузки, мониторинг промышленных процессов и финансовый анализ, модели сталкиваются с обработкой огромных объемов данных. Необходимость в моделях, способных эффективно обрабатывать эти большие наборы наблюдений, обусловлена не только объемом данных, но и сложностью извлекаемых закономерностей. Традиционные модели часто демонстрируют снижение производительности при увеличении длины временного ряда или количества анализируемых переменных. Модели, предназначенные для работы с большими наблюдениями (Large Observation Models), позволяют преодолеть эти ограничения за счет оптимизации архитектуры и алгоритмов обработки данных, обеспечивая более точные и надежные результаты при анализе сложных временных рядов.

Архитектуры PatchTST и TimesFM-ICF повышают эффективность работы моделей временных рядов за счет использования локальной семантической информации и обучения в контексте (in-context learning). PatchTST разбивает входные данные на небольшие фрагменты (патчи), позволяя модели фокусироваться на локальных зависимостях во временном ряду и эффективно обрабатывать длинные последовательности. TimesFM-ICF использует частотно-модулированный (frequency modulation) подход и концепцию информационного сжатия (information compression) для извлечения релевантных локальных признаков и улучшения способности модели к обобщению. Обе архитектуры позволяют модели адаптироваться к новым данным без значительного изменения параметров, используя информацию, содержащуюся непосредственно в контексте входных данных.

Метод адаптации с низким рангом (LoRA) представляет собой параметрически-эффективную технику тонкой настройки, предназначенную для адаптации причинно-следственных трансформаторов к конкретным задачам. Вместо обновления всех параметров предобученной модели, LoRA замораживает веса и вводит обучаемые матрицы низкого ранга в каждый слой трансформатора. Это значительно сокращает количество обучаемых параметров, обычно на несколько порядков, что снижает требования к вычислительным ресурсам и объему памяти, необходимые для тонкой настройки. В процессе обучения обновляются только матрицы низкого ранга, в то время как исходные веса трансформатора остаются неизменными, что позволяет избежать катастрофического забывания и сохранить обобщающую способность модели. $R$ — ранг используемых матриц, определяющий компромисс между параметрической эффективностью и производительностью.

Методы, такие как PatchTST, TimesFM-ICF и LoRA, позволяют эффективно масштабировать модели временных рядов для работы с большими объемами данных и высокой размерностью признаков. PatchTST и TimesFM-ICF используют локальную семантическую информацию и обучение в контексте для улучшения производительности, в то время как LoRA обеспечивает параметрически-эффективную тонкую настройку причинно-следственных трансформаторов. Это достигается за счет снижения вычислительных затрат и требований к памяти, позволяя обучать и адаптировать модели к конкретным задачам даже при ограниченных ресурсах, что критически важно для реальных приложений, генерирующих сложные и многомерные данные.

Анализ производных цены и объема, полученных SplineGPT, выявляет сложную структуру высокочастотного сигнала, отражающую волатильность и ускорение потока объема, что позволяет более четко определить момент капитуляции и последующего восстановления акций Pfizer (PFE) по сравнению с традиционным графиком OHLC.

К активному управлению рисками: Интеграция физики и обоснованных решений

Эффективное управление рисками требует точного прогнозирования потенциальных убытков, для чего используются ключевые показатели, такие как максимальная просадка (Maximum Drawdown), коэффициент Шарпа (Sharpe Ratio) и коэффициент сортино (Sortino Ratio). Максимальная просадка определяет наибольшее падение стоимости актива от пика до минимума, демонстрируя потенциальные потери в неблагоприятном сценарии. Коэффициент Шарпа оценивает доходность с поправкой на риск, позволяя сравнить различные инвестиционные стратегии. В свою очередь, коэффициент сортино фокусируется на рисках падения, учитывая только отрицательные отклонения от средней доходности. Комбинированное использование этих метрик позволяет всесторонне оценить риски и доходность инвестиций, обеспечивая основу для принятия обоснованных решений и сохранения капитала, особенно в условиях волатильности рынка.

Логика импульса служит основой для выявления и использования ценовых трендов. Данный подход предполагает, что активы, демонстрирующие устойчивый рост или падение в прошлом, с большей вероятностью продолжат движение в том же направлении и в будущем. В основе лежит идея о том, что рыночные тенденции обладают инерцией, и текущие движения цен не являются случайными, а отражают существующий импульс. Анализ импульса позволяет выделить активы с высоким потенциалом роста или падения, предоставляя возможность для формирования торговых стратегий, направленных на извлечение прибыли из продолжительности трендов. Успешное применение данной логики требует точного определения силы и продолжительности импульса, а также своевременной корректировки стратегии в зависимости от изменений на рынке.

В основе подхода, использующего искусственный интеллект, обогащенного физическими принципами, лежит интеграция фундаментальных законов природы непосредственно в процесс моделирования. Техники, такие как сети, обусловленные физикой ( $Physics-Informed Neural Networks$ ), позволяют не просто анализировать данные, но и учитывать известные физические ограничения и взаимосвязи. Это существенно повышает надежность и точность прогнозов, особенно в сложных динамических системах, где традиционные методы машинного обучения могут давать сбои из-за недостатка обобщающей способности. Вместо слепого подражания историческим данным, модель стремится к решению, которое физически правдоподобно и соответствует установленным законам, что обеспечивает более устойчивые и предсказуемые результаты даже в условиях высокой волатильности и непредсказуемости рынка.

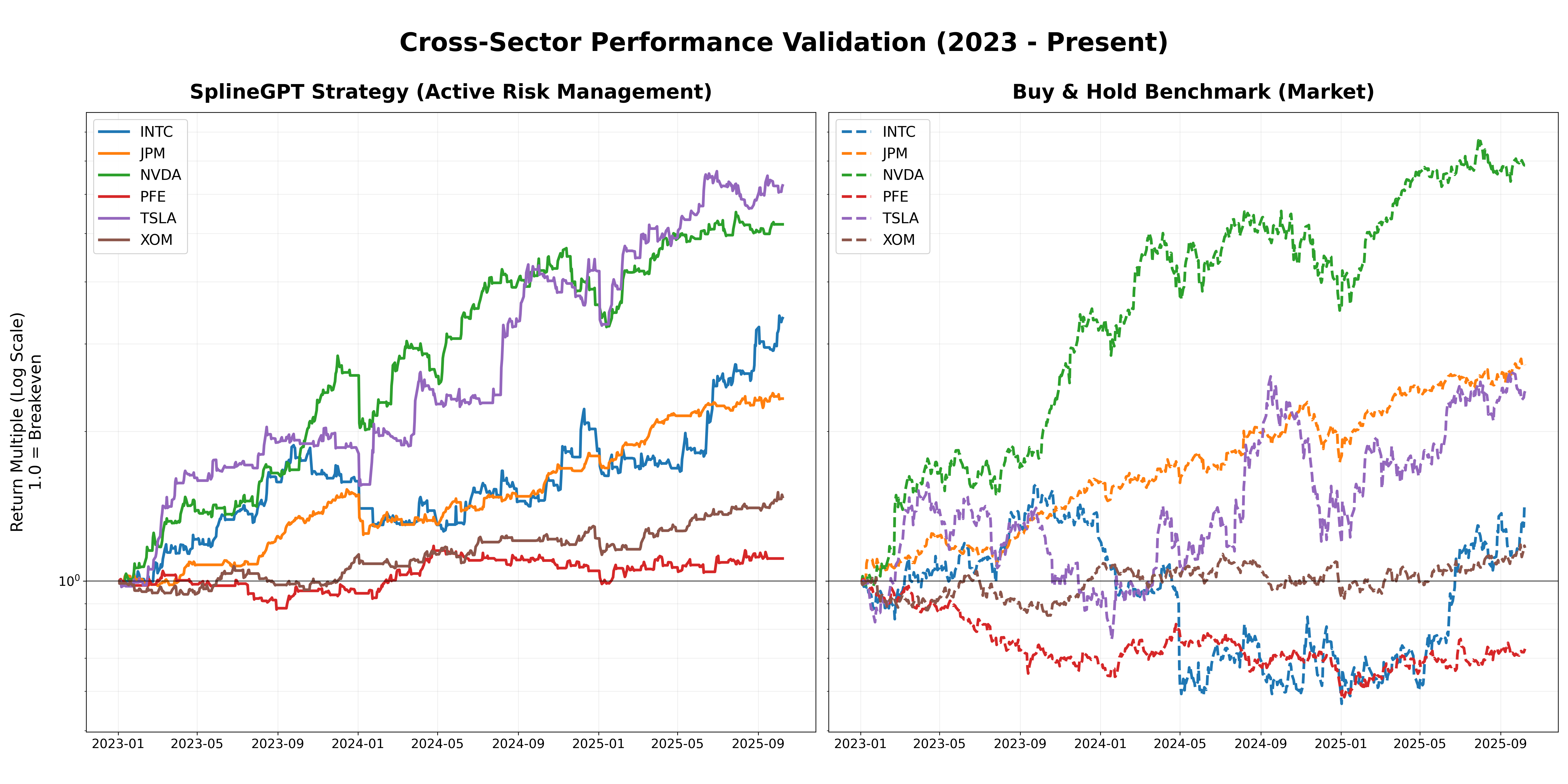
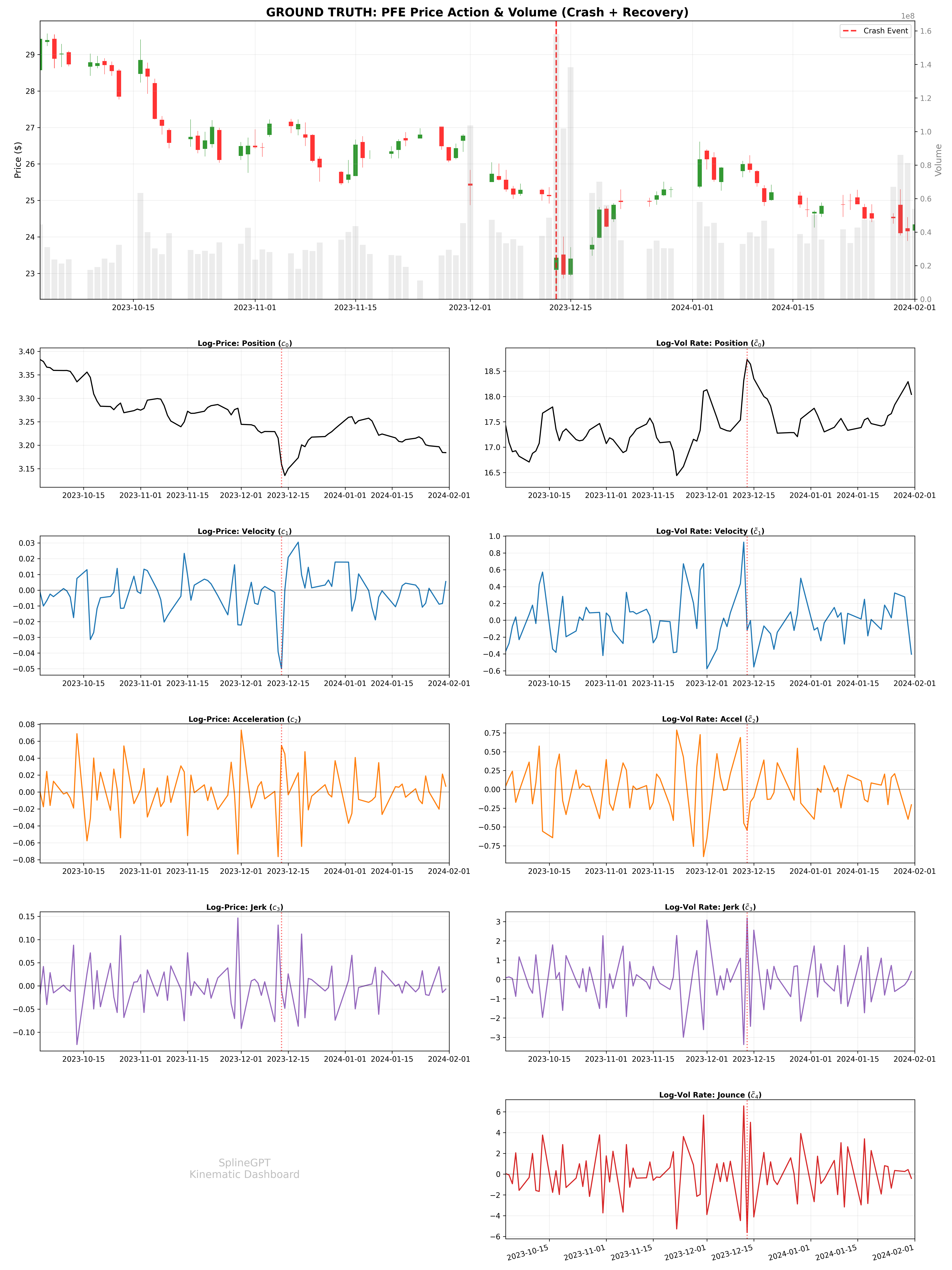
Предложенная методология, объединяющая принципы физики и искусственный интеллект, демонстрирует значительное повышение точности прогнозирования и снижение рисков при принятии решений в сложных системах. Практическая реализация позволила достичь коэффициента Шарпа до 1.42, что свидетельствует о высокой доходности с учетом риска. В условиях резкого обвала рынка, смоделированного на примере акций Pfizer (PFE), система сохранила капитал, ограничившись максимальной просадкой в -18.8%. При этом, разработанная модель характеризуется высокой частотой операций — оборачиваемость капитала варьируется от 36x до 86x — и сохраняет положительные значения коэффициента Шарпа даже при учете транзакционных издержек до 20 базисных пунктов, что подтверждает её эффективность и применимость в реальных торговых условиях.

Модель продемонстрировала быструю адаптацию к ложному пробою, мгновенно отреагировав на изменение ускорения [latex]c2c_{2}[/latex] после первоначального сигнала [latex]c1c_{1}[/latex] и переключившись на позицию “Продать”, что позволило избежать убытков при последующем падении рынка на ≈10%, и объясняет низкие показатели максимальной просадки. — Модель продемонстрировала быструю адаптацию к ложному пробою, мгновенно отреагировав на изменение ускорения $c2c_{2}$ после первоначального сигнала $c1c_{1}$ и переключившись на позицию “Продать”, что позволило избежать убытков при последующем падении рынка на ≈10%, и объясняет низкие показатели максимальной просадки.

Исследование, представленное в данной работе, демонстрирует, что подход к обработке временных рядов не должен ограничиваться дискретными представлениями. Авторы предлагают SplineGPT, модель, использующую сплайны для непрерывной токенизации, что позволяет извлекать кинематические особенности высокого порядка. Это напоминает высказывание Кena Thompson: «Всякий раз, когда думаешь, что все под контролем, значит, что-то упустил». Ведь стремление к упрощению и дискретизации данных может скрывать важные нюансы, влияющие на долгосрочную стабильность системы. Работа подчеркивает, что долгосрочное функционирование модели требует понимания не только текущего состояния, но и динамики изменений, что особенно важно при работе с зашумленными временными рядами и управлении рисками.

Что дальше?

Представленная работа, как и любая попытка обуздать хаос временных рядов, скорее выявляет новые области для пророческих ошибок, чем предлагает окончательные решения. Непрерывное токенизирование сплайнами, безусловно, позволяет извлекать более тонкие кинематические признаки, но каждый новый деплой — это лишь отсрочка неизбежного столкновения с непредсказуемостью рынка. Улучшение показателей, основанное на извлечении производных, — это иллюзия контроля, ведь даже самые элегантные модели оказываются уязвимыми к шуму, который, в конечном счете, определяет реальность.

Следующим шагом видится не столько усложнение архитектуры, сколько признание её фундаментальной неполноты. Акцент должен сместиться с предсказания будущих цен на активное управление рисками, на создание систем, способных адаптироваться к неминуемым провалам. Идея «основополагающих моделей» требует переосмысления: возможно, вместо построения единой, всеобъемлющей модели, стоит стремиться к созданию роя специализированных агентов, каждый из которых отвечает за определенный аспект риска.

Документация? Кто пишет пророчества после их исполнения? Этот труд лишь подчеркивает, что каждая архитектурная оптимизация — это заявление о будущем сбое. Вместо поиска «идеального» токенизатора, необходимо научиться жить с неточностями и строить системы, которые процветают в условиях неопределенности. И тогда, возможно, удастся создать не модель рынка, а экосистему, способную выживать в его хаосе.

Оригинал статьи: https://arxiv.org/pdf/2601.09949.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-16 21:43