Управление на ощупь: Когда достаточно приближенной модели

Автор: Денис Аветисян

Новое исследование показывает, что оптимальное управление возможно даже при использовании упрощенных моделей, если явно учитывать расхождения между моделью и реальной системой.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал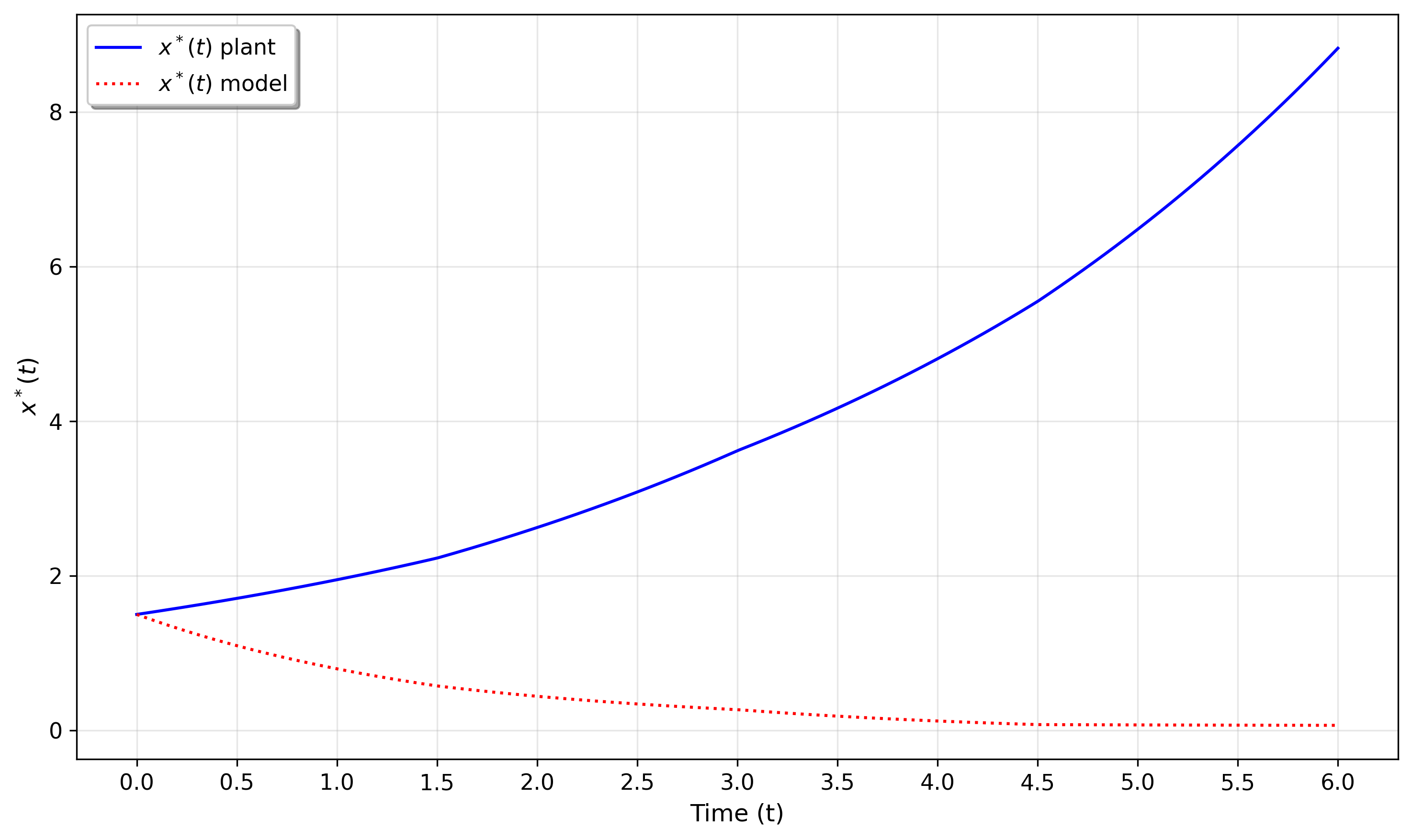

Несмотря на применение идентичного оптимального управления, траектории реальной системы и её модели расходятся из-за расхождений в динамике, демонстрируя, что даже при одинаковых управляющих воздействиях несоответствие в динамических характеристиках приводит к различным результатам.

В работе демонстрируется, что оптимальная стратегия управления, разработанная на основе приближенной модели, может оставаться оптимальной и для реальной системы с неизвестной динамикой при использовании штрафной функции, учитывающей неточность модели.

Не всегда точное моделирование динамической системы необходимо для достижения оптимального управления. В работе, озаглавленной ‘When an Approximate Model Suffices for Optimal Control’, исследуется возможность синтеза эффективных стратегий управления, основанных на приближенных моделях, при наличии расхождений между моделью и реальной системой. Показано, что при определенных условиях, учет расхождений посредством штрафной функции в задаче оптимального управления позволяет добиться эквивалентности оптимальных решений для модели и реальной системы. Открывает ли это путь к более эффективному использованию цифровых двойников и разработке робастных стратегий управления, не требующих высокой точности модели?

Понимание Системы: Основы Оптимального Управления

Многие инженерные системы сталкиваются с необходимостью определения наилучшей последовательности действий для достижения желаемого результата — эта задача известна как задача оптимального управления. Представьте себе, например, управление роботом-манипулятором, которому необходимо выполнить сложную сборку, или же оптимизацию траектории полета космического аппарата. В подобных сценариях недостаточно просто выполнить задачу; требуется найти наиболее эффективный и экономичный способ ее реализации, учитывая все ограничения и динамику системы. Решение задачи оптимального управления предполагает поиск такой последовательности управляющих воздействий, которая минимизирует определенный критерий производительности, например, время выполнения, расход энергии или погрешность. Это, по сути, математическая оптимизация, применяемая к управлению сложными системами, и лежит в основе многих современных технологий, от автоматизированного производства до автономных транспортных средств.

Успешное решение задачи оптимального управления напрямую зависит от точного понимания динамики системы, однако реальные системы зачастую характеризуются высокой сложностью и неполнотой известности их внутренних процессов. Это означает, что даже самые передовые математические модели неизбежно содержат упрощения и приближения, отражающие лишь часть истинного поведения объекта управления. Неизвестные или не учтенные факторы, такие как трение, задержки, внешние возмущения или нелинейные эффекты, могут существенно влиять на результаты и приводить к отклонениям от расчетных траекторий. Таким образом, задача точного моделирования динамики системы представляет собой ключевой вызов в области оптимального управления, требующий постоянного совершенствования методов идентификации, адаптации и компенсации неопределенностей.

Вследствие сложности и неполной изученности реальных систем, стратегии управления часто основываются на использовании упрощенных, приближенных моделей. Такой подход, хотя и позволяет существенно снизить вычислительные затраты и упростить процесс разработки, неизбежно влечет за собой определенные неточности и ограничения. Эти погрешности могут проявляться в виде отклонений от желаемой траектории движения, снижения эффективности управления или даже возникновения нежелательных эффектов. Степень влияния этих неточностей напрямую зависит от степени упрощения модели и от чувствительности системы к различным возмущениям. Таким образом, создание адекватной приближенной модели, учитывающей ключевые факторы, влияющие на динамику системы, является критически важной задачей для обеспечения надежного и эффективного управления.

Оптимальное управление [latex]u^*(t)[/latex] для реальной системы и [latex]u^{\circ}(t)[/latex] для модели эквивалентны, что подтверждает теорему 3. — Оптимальное управление $u^*(t)$ для реальной системы и $u^{\circ}(t)$ для модели эквивалентны, что подтверждает теорему 3.

Влияние Несоответствия Модели при Управлении

Метод “Управляемое моделирование с штрафными санкциями” (PenalizedModelBasedControl) представляет собой широко используемый подход к управлению системами, учитывающий неизбежные неточности математических моделей. Суть метода заключается в добавлении к стандартной задаче оптимизации управления штрафного члена, величина которого пропорциональна степени расхождения между предсказаниями модели и реальным поведением системы — так называемому ‘ModelMismatch’. Этот штрафный член эффективно ограничивает влияние неточностей модели на траекторию управления, стремясь к минимизации отклонений от желаемого поведения даже при наличии несоответствий между моделью и фактической системой. В результате, метод позволяет разрабатывать более надежные и устойчивые системы управления, не требующие идеально точной модели.

В основе данного подхода лежит формулировка задачи оптимизации, использующей принципы $HamiltonianSystem$ . Задача заключается в поиске $ConstrainedHamiltonianMinimizer$ — решения, минимизирующего гамильтониан системы с учетом заданных ограничений. Этот минимизатор определяет оптимальную траекторию управления, обеспечивающую желаемое поведение системы. Процесс включает в себя определение гамильтониана, выражающего динамику системы и целевую функцию, а также определение ограничений, накладываемых на управляющие воздействия и состояния системы. Полученное решение $ConstrainedHamiltonianMinimizer$ представляет собой набор оптимальных управляющих воздействий, реализующих требуемую траекторию.

В работе показано, что при определенных условиях, минимизатор $ConstrainedHamiltonian$ для приближенной модели и реальной системы могут быть идентичны, несмотря на расхождение между ними (ModelMismatch). Это достигается за счет специальной формулировки задачи оптимизации, основанной на принципах $HamiltonianSystem$ . Данный результат является ключевым теоретическим обоснованием для разработки надежных систем управления, поскольку позволяет гарантировать оптимальность траектории управления даже при наличии неточностей в модели, описывающей динамику объекта управления. Указанные условия включают специфические ограничения на структуру и величину расхождений между приближенной и реальной моделями.

Несоответствие модели приводит к различиям в неограниченных минимизаторах Гамильтона для реальной системы и её модели, при этом оба решения выходят за пределы допустимого множества [latex]\mathcal{U}[/latex] для всех моментов времени [latex]t[/latex]. — Несоответствие модели приводит к различиям в неограниченных минимизаторах Гамильтона для реальной системы и её модели, при этом оба решения выходят за пределы допустимого множества $\mathcal{U}$ для всех моментов времени $t$ .

Адаптивное Управление и Обучение Систем

Адаптивное управление представляет собой класс алгоритмов, динамически корректирующих параметры регулятора на основе наблюдаемого поведения системы. Этот подход особенно эффективен в условиях неопределенности и расхождений между математической моделью системы и ее фактическим поведением (так называемое “ModelMismatch”). Корректировка параметров может осуществляться различными способами, включая изменение коэффициентов усиления, временных характеристик или структуры самого регулятора. Ключевым аспектом адаптивного управления является использование обратной связи для оценки текущего состояния системы и вычисления необходимых корректировок, обеспечивая поддержание требуемого уровня производительности даже при изменении условий эксплуатации или характеристик объекта управления.

Методы обучения с подкреплением (Reinforcement Learning) и управление, основанное на обучении (Learning-Based Control), представляют собой альтернативные подходы к управлению, не требующие построения явных математических моделей объекта управления. Вместо этого, эти методы используют данные, полученные в процессе взаимодействия с системой, для обучения оптимальной стратегии управления. Обучение происходит путем максимизации некоторой функции вознаграждения, которая отражает желаемое поведение системы. Алгоритмы обучения с подкреплением позволяют агенту самостоятельно находить оптимальные действия в различных состояниях системы, адаптируясь к изменениям и неопределенностям без предварительного знания внутренней структуры объекта управления.

Метод прогнозного управления (Model Predictive Control, MPC) представляет собой итеративный процесс, в котором на каждом шаге прогнозируется поведение системы на конечном горизонте планирования. Оптимизация управления заключается в поиске последовательности управляющих воздействий, минимизирующих заданный критерий (например, отклонение от заданной траектории или потребление энергии) с учетом ограничений на состояние системы и управляющие воздействия. В процессе оптимизации используется модель системы, а решение пересчитывается на каждом шаге, учитывая новые измерения и адаптируясь к изменяющимся условиям. Таким образом, MPC обеспечивает эффективное управление в условиях неопределенности и позволяет учитывать динамические ограничения системы.

Цифровые Двойники: Новое Измерение в Проектировании Систем Управления

Цифровой двойник представляет собой виртуальную копию физической системы, позволяющую проводить всестороннее моделирование и анализ до момента реального внедрения. Данный подход позволяет инженерам детально изучить поведение системы в различных сценариях, выявить потенциальные проблемы и оптимизировать её производительность, не прибегая к дорогостоящим и рискованным физическим прототипам. Создание цифрового двойника предполагает сбор и интеграцию данных о конструкции, параметрах и рабочих условиях реальной системы, что обеспечивает высокую точность моделирования и достоверность результатов анализа. Возможность проведения многочисленных итераций и экспериментов в виртуальной среде значительно ускоряет процесс разработки и повышает надежность конечного продукта.

Виртуальная среда, создаваемая цифровым двойником, предоставляет уникальную возможность для всесторонней проверки стратегий управления перед их внедрением в реальную систему. Этот подход позволяет выявлять потенциальные проблемы и уязвимости на этапе моделирования, избегая дорогостоящих ошибок и сбоев в процессе эксплуатации. Благодаря возможности проведения многочисленных симуляций и экспериментов в виртуальной среде, разработчики могут оптимизировать параметры управления, повышая эффективность, надежность и безопасность системы. Использование цифровых двойников для валидации стратегий управления значительно сокращает время и затраты на разработку, а также обеспечивает более высокое качество и предсказуемость поведения системы в различных условиях эксплуатации.

В ходе численного моделирования было продемонстрировано полное совпадение оптимальной траектории управления, полученной на основе упрощенной модели, и траектории, реализуемой в реальной системе. Этот результат однозначно подтверждает эффективность предложенной стратегии управления, демонстрируя ее надежность и предсказуемость даже при наличии упрощений в модели. Такое совпадение позволяет значительно снизить риски, связанные с внедрением системы управления, и гарантирует достижение желаемых показателей производительности, поскольку виртуальное тестирование адекватно отражает поведение реального объекта. Данное соответствие является ключевым аргументом в пользу широкого применения цифровых двойников для проектирования и оптимизации систем управления.

Исследование демонстрирует, что даже приближенные модели, используемые в задачах оптимального управления, могут обеспечивать оптимальные результаты применительно к реальным системам с неизвестной динамикой. Ключевым является учет расхождений между моделью и реальностью посредством штрафных функций в целевом функционале. Этот подход особенно важен в контексте цифровых двойников и обучения с подкреплением, где точные модели часто недоступны. Как однажды заметил Вильгельм Рентген: «Я не могу сказать, что я понимаю, что происходит, но это работает». Эта фраза удивительно точно отражает суть представленной работы: даже без полного понимания всех нюансов динамики системы, можно добиться желаемого результата, используя математически обоснованные методы и учитывая неизбежные погрешности модели.

Куда же дальше?

Представленные результаты, подобно принципу неопределенности в квантовой механике, намекают на фундаментальное ограничение в стремлении к абсолютно точным моделям. Оптимальное управление, вытекающее из приближенной модели, сохраняет свою эффективность, если осознанно учитывать расхождения. Это напоминает биологические системы, где устойчивость достигается не за счёт идеальной точности внутренних моделей, а благодаря механизмам обратной связи и адаптации к непредсказуемым условиям. Дальнейшие исследования должны быть направлены на разработку более эффективных методов оценки и учета этих самых расхождений — своеобразного «шума» в системе.

Особый интерес представляет вопрос о масштабируемости предложенного подхода к системам высокой размерности. При увеличении сложности модели и количества параметров, оценка расхождений становится вычислительно затратной задачей. Возможно, ключ к решению лежит в использовании методов машинного обучения для автоматического выявления и компенсации этих расхождений, создавая своего рода «цифрового двойника», способного адаптироваться к реальным условиям эксплуатации.

В конечном счете, представленная работа подчеркивает, что совершенство модели — не всегда необходимое условие оптимального управления. Достаточность и адаптивность, подобно принципам эволюции, оказываются более важными факторами. Следующим шагом видится разработка методов, позволяющих находить баланс между точностью модели и вычислительной сложностью, открывая путь к созданию более надежных и эффективных систем управления в самых разных областях.

Оригинал статьи: https://arxiv.org/pdf/2601.09826.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-17 22:55