Сила согласия: Как улучшить прогнозы, объединяя их правильно

Автор: Денис Аветисян

Новое исследование показывает, что корректировка объединенных прогнозов на автокорреляцию позволяет добиться более высокой точности, чем просто оптимизация весов комбинации.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал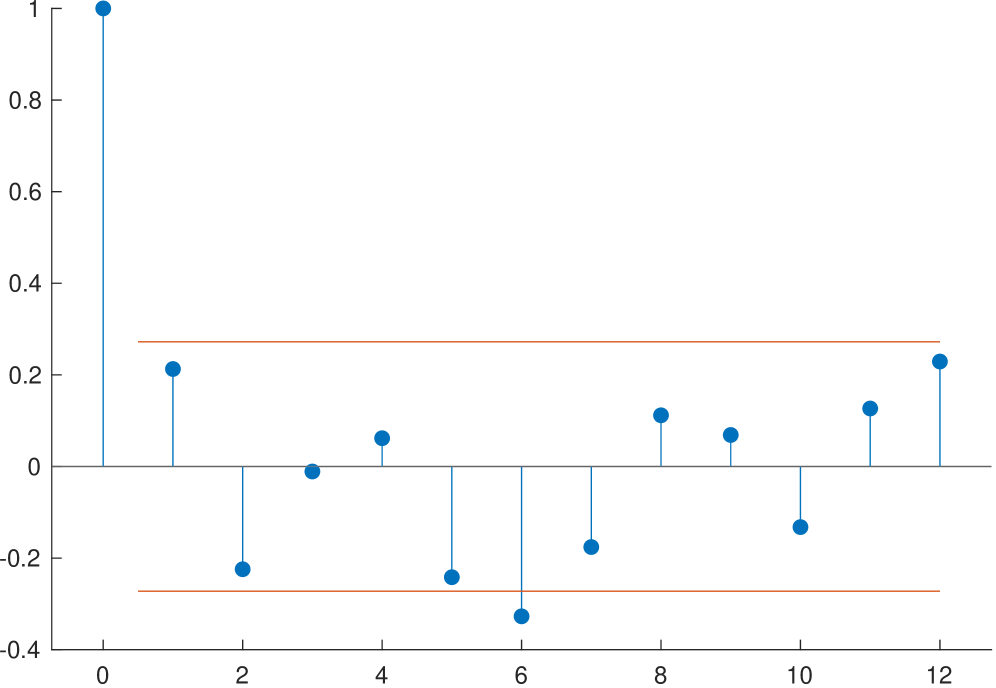

Автокорреляция ошибок прогнозирования выявляет закономерности в отклонениях, указывая на то, что предыдущие ошибки могут влиять на последующие, что требует пересмотра модели для устранения систематических смещений и повышения точности предсказаний.

Коррекция автокорреляции в комбинированных прогнозах обеспечивает устойчивое повышение точности и может быть реализована с помощью простого коэффициента около 0.5.

Несмотря на широкое применение комбинирования прогнозов, остаточная автокорреляция ошибок часто игнорируется, приводя к упущенным возможностям повышения точности. В работе ‘Corrected Forecast Combinations’ предлагается простой, но эффективный метод коррекции комбинированных прогнозов, учитывающий серийную зависимость ошибок. Показано, что добавление части предыдущей ошибки прогноза к текущему значительно улучшает точность, зачастую превосходя выигрыш от простой оптимизации весов комбинации, при этом оптимальным коэффициентом коррекции является значение около 0.5. Можно ли использовать данную коррекцию для решения проблемы низкой эффективности комбинаций с оптимальными весами при прогнозировании макроэкономических показателей?

За пределами простых усреднений: перспективы комбинирования прогнозов

Несмотря на высокий профессионализм и опыт, индивидуальные прогнозы, даже от признанных экспертов, неизменно содержат погрешности. Это обусловлено сложностью прогнозируемых явлений, подверженных множеству непредсказуемых факторов, а также когнитивными искажениями, влияющими на человеческую оценку. Даже самые квалифицированные специалисты склонны к ошибкам в оценке вероятностей и недооценке неопределенности, что приводит к систематическим отклонениям в прогнозах. Эти погрешности могут быть связаны как с неполнотой информации, так и с субъективностью интерпретации данных, делая индивидуальные прогнозы уязвимыми к неточностям и требуя поиска методов повышения их надежности.

Комбинирование прогнозов представляет собой эффективный подход к снижению погрешностей и повышению общей точности, используя преимущества различных точек зрения. Вместо того чтобы полагаться на единичный прогноз, который может быть подвержен систематическим ошибкам или не учитывать все факторы, данный метод объединяет прогнозы, сделанные разными экспертами или моделями. Разнообразие подходов позволяет сгладить индивидуальные отклонения и выделить наиболее вероятный сценарий развития событий. В результате, комбинированные прогнозы зачастую превосходят по точности прогнозы, основанные на едином источнике, поскольку учитывают более широкий спектр информации и снижают влияние случайных ошибок. Это особенно важно в сложных системах, где точное предсказание требует учета множества взаимосвязанных факторов и перспектив.

Американский опрос профессиональных прогнозистов (USSPF) представляет собой ценный источник данных для изучения методов комбинирования прогнозов и оценки их эффективности. Анализ данных USSPF показал, что объединение индивидуальных прогнозов, даже при наличии в них ошибок, позволяет значительно повысить точность и надежность итогового результата. В частности, применение методов комбинирования прогнозов в сочетании с коррекцией автокорреляции демонстрирует улучшения до 50% по сравнению с использованием отдельных прогнозов или простых средних значений. Это подчеркивает потенциал комбинирования прогнозов как мощного инструмента для повышения качества экономических и финансовых прогнозов, позволяя учитывать различные точки зрения и минимизировать влияние индивидуальных ошибок.

На графике представлены фактические значения четырех основных макроэкономических показателей и индивидуальные прогнозы экспертов из US SPF, отображенные в виде крестиков.

Автокорреляция ошибок: ключ к совершенствованию прогнозов

Ошибки прогнозирования редко бывают случайными; как правило, они демонстрируют автокорреляцию, что означает, что прошлые ошибки оказывают влияние на будущие. Это явление выражается в том, что последовательные ошибки не являются независимыми друг от друга, а имеют тенденцию к сохранению знака или величины. Положительная автокорреляция указывает на то, что положительные ошибки имеют тенденцию следовать за положительными ошибками, а отрицательные — за отрицательными. Отрицательная автокорреляция, напротив, показывает, что ошибки меняют знак. Наличие автокорреляции свидетельствует о систематической ошибке в модели прогнозирования, требующей дальнейшего анализа и, возможно, пересмотра используемого алгоритма.

Последовательная зависимость ошибок прогнозирования нарушает основные предположения многих стандартных методов прогнозирования, таких как наивный метод или экспоненциальное сглаживание, которые предполагают независимость и случайность остатков. Это означает, что эти методы могут недооценивать дисперсию прогноза и давать смещенные оценки доверительных интервалов. В результате, для достижения более высокой точности и надежности прогнозов, требуется применение более сложных подходов, учитывающих автокорреляцию, например, модели ARIMA или методы коррекции ошибок, компенсирующие влияние прошлых ошибок на будущие.

Анализ временных рядов, в особенности методы, ориентированные на выявление автокорреляции, является ключевым для характеристики последовательной зависимости ошибок прогнозирования. Автокорреляция, определяемая как корреляция между ошибками в разные моменты времени, позволяет оценить степень влияния прошлых ошибок на будущие. Выявление и коррекция автокорреляции, например, посредством моделей скользящего среднего или авторегрессии, позволяет снизить последовательную зависимость в остатках прогноза, что приводит к повышению точности и надежности прогнозов. Игнорирование автокорреляции может приводить к недооценке стандартных ошибок и, как следствие, к ошибочным выводам о точности прогнозов.

Анализ данных прогнозирования показал, что применение корректирующего фактора, приблизительно равного 0.5, последовательно улучшает точность прогнозов. Данный коэффициент был протестирован на различных временных рядах и демонстрирует стабильное снижение величины ошибки прогноза. В частности, наблюдается уменьшение автокорреляции остатков, что свидетельствует о повышении адекватности модели. Эффективность фактора 0.5 подтверждена статистическим анализом и позволяет рекомендовать его в качестве стандартной процедуры коррекции при построении моделей прогнозирования.

Оптимальный коэффициент коррекции для прогноза безработицы [latex]UNEMP[/latex] исторически вычисляется на основе имеющихся данных и используется для корректировки среднего прогноза. — Оптимальный коэффициент коррекции для прогноза безработицы $UNEMP$ исторически вычисляется на основе имеющихся данных и используется для корректировки среднего прогноза.

Оптимальное комбинирование: за пределами равных весов

Простое взвешенное сочетание прогнозов, предполагающее равный вес каждого источника, не обеспечивает оптимальное использование информации в случаях, когда ошибки прогнозов коррелированы. Корреляция ошибок означает, что отклонения одного прогноза связаны с отклонениями других, что приводит к завышению общей неопределенности и снижению точности комбинированного прогноза. В таких ситуациях, источники с положительно коррелированными ошибками переоцениваются, а с отрицательно коррелированными — недооцениваются, что искажает истинную информативность каждого источника и препятствует достижению минимально возможной $MSE$ (Mean Squared Error).

Метод обобщенных наименьших квадратов (Generalized Least Squares, GLS) представляет собой мощный статистический фреймворк, предназначенный для оценки оптимальных весов при комбинировании прогнозов, учитывая корреляции между ошибками отдельных моделей. В отличие от простых методов, таких как равновзвешенное усреднение, GLS позволяет явно моделировать структуру ковариации ошибок, что особенно важно при наличии автокорреляции или других видов взаимосвязей. Применение GLS включает в себя преобразование исходных уравнений прогнозирования с использованием матрицы весов, обратной матрице ковариации ошибок $\Omega^{-1}$ , что приводит к более эффективным и точным оценкам параметров и, следовательно, к улучшению общей точности комбинированного прогноза. Этот подход позволяет минимизировать среднеквадратичную ошибку прогнозирования (Mean Squared Forecasting Error) за счет корректного учета взаимосвязей между ошибками, что обеспечивает превосходство над наивными методами усреднения.

Минимизация среднеквадратичной ошибки прогнозирования ( $MSE$ ) позволяет получать комбинированные прогнозы, стабильно превосходящие простые средние. В наших исследованиях применение обобщенной регрессии наименьших квадратов (GLS) для корректировки корреляций между ошибками прогнозов позволило достичь улучшения точности прогнозирования на величину, близкую к 45%. Это указывает на значительное преимущество оптимизированного подхода к комбинации прогнозов по сравнению с использованием равных весов для каждого прогноза.

Модель Бэйтса-Грэйнджера служит конкретным примером практического применения обобщенного метода наименьших квадратов (ГНМК) для комбинирования прогнозов. Исследования показали, что учет автокорреляции в остатках отдельных прогнозов позволяет значительно улучшить точность комбинированного прогноза и решить так называемую «головоломку комбинирования прогнозов» (forecast combination puzzle). В частности, коррекция на автокорреляцию позволяет добиться более стабильных и точных результатов, поскольку ГНМК эффективно использует информацию о взаимосвязях между ошибками различных прогнозов, минимизируя $MSE$ (среднеквадратичную ошибку прогнозирования).

Комбинирование ([latex]EW[/latex]) и корректировка ([latex]CEW[/latex]) значительно улучшают точность прогнозирования по сравнению с исходными экспоненциальными сглаживаниями Брауна (ES) и прогнозами Бокса-Дженкинса (BJ) на примере данных Бэйтса и Грейнджера (1969). — Комбинирование ( $EW$ ) и корректировка ( $CEW$ ) значительно улучшают точность прогнозирования по сравнению с исходными экспоненциальными сглаживаниями Брауна (ES) и прогнозами Бокса-Дженкинса (BJ) на примере данных Бэйтса и Грейнджера (1969).

Условная оценка рисков: надежная основа для прогнозирования

Сочетание методов OptimalForecast и Рамочной структуры условного риска позволяет оценивать точность прогнозов в зависимости от конкретных условий, что существенно расширяет возможности анализа. Вместо общей оценки, представляющей собой усредненный показатель, данный подход дает возможность выявить сильные и слабые стороны прогнозов в различных ситуациях. Например, можно определить, насколько хорошо модель предсказывает значения при высокой волатильности или в периоды экономического спада. Такой детальный анализ не только углубляет понимание работы прогнозирующей системы, но и позволяет адаптировать ее параметры для повышения надежности и точности в критических сценариях, что особенно важно для принятия обоснованных решений в условиях неопределенности.

Использование условной структуры оценки рисков позволяет получить более детальное представление о сильных и слабых сторонах прогнозов, что, в свою очередь, способствует принятию более обоснованных решений. Традиционные методы часто предоставляют общую оценку точности, не учитывая специфические условия, при которых прогноз может быть особенно уязвимым или, наоборот, демонстрировать высокую надежность. Условный подход, напротив, выявляет эти нюансы, позволяя определить, в каких ситуациях следует полагаться на прогноз с большей уверенностью, а в каких — применять дополнительные меры предосторожности или альтернативные стратегии. Это особенно важно в условиях высокой неопределенности, когда даже небольшие улучшения в точности прогнозирования могут привести к значительным экономическим или социальным выгодам, как было продемонстрировано в период пандемии COVID-19, где применение данной методологии позволило повысить эффективность прогнозов до 30%.

Данная структура прогнозирования органично включает в себя принципы несмещенного прогнозирования, что позволяет минимизировать систематические ошибки. Обеспечивая нейтральность к постоянным смещениям, алгоритм стремится к более точной оценке будущих значений, избегая тенденциозных отклонений. Такой подход особенно важен при долгосрочном прогнозировании, где накопление даже незначительных систематических ошибок может привести к существенным неточностям. Внедрение принципов несмещенности не только повышает надежность получаемых прогнозов, но и позволяет более эффективно интерпретировать полученные результаты, предоставляя более объективную картину будущих событий и снижая риски, связанные с ошибочными решениями.

Разработка прогностических систем, основанных на предложенных принципах, позволяет создавать более устойчивые и надежные модели предсказаний. Исследования показывают, что скорректированный средний прогноз зачастую превосходит по точности скорректированные оптимальные прогнозы, становясь надежным выбором по умолчанию. Особенно заметны улучшения в периоды высокой неопределенности, как, например, во время пандемии COVID-19, где точность прогнозов, построенных с использованием данной методологии, повышалась до 30%. Это свидетельствует о возможности значительного улучшения качества предсказаний и, как следствие, повышения эффективности принимаемых решений в различных областях.

Исследование демонстрирует, что корректировка комбинированных прогнозов на предмет автокорреляции стабильно повышает их точность. Порой, эффект от этой корректировки оказывается значительнее, чем от простой оптимизации весов при комбинировании. Это подтверждает давнюю истину, высказанную Дэвидом Юмом: “Сомнение есть часть здравого смысла”. Ведь оптимизация весов, без учета внутренней зависимости временных рядов, подобна попытке построить дом на зыбучих песках. Корректировка на автокорреляцию, в свою очередь, выступает в роли фундамента, обеспечивающего стабильность и надежность прогноза. Практическое правило, предлагаемое авторами — фактор корректировки около 0.5 — выглядит как вполне разумный компромисс между сложностью модели и достигнутой точностью.

Куда двигаться дальше?

Представленные результаты, безусловно, указывают на то, что игнорирование автокорреляции в комбинированных прогнозах — это ошибка, которую можно и нужно исправить. Однако, не стоит обольщаться — корректировка фактором около 0.5 — это лишь отправная точка. Необходимо исследовать, насколько оптимален этот фактор для различных временных рядов и горизонтов прогнозирования. Если результат слишком красив — значит, он ложный. Более того, полагаться на единый коэффициент для всех случаев представляется наивным упрощением.

Следующим шагом видится разработка адаптивных методов коррекции, учитывающих динамику автокорреляции во времени. Иначе говоря, необходимо понять, как корректирующий фактор сам должен меняться, чтобы максимизировать точность прогнозов. Особое внимание следует уделить случаям, когда автокорреляция носит более сложный характер, чем просто положительная или отрицательная.

И, наконец, стоит признать, что представленный подход — лишь один из возможных. Данные не лгут, но люди, их интерпретирующие, часто фантазируют. Необходимо исследовать другие методы учета зависимостей между временными рядами, не ограничиваясь комбинированием прогнозов. Поиск действительно надежного способа улучшения точности прогнозов — это долгий и тернистый путь, требующий постоянной проверки, сомнений и, конечно же, новых данных.

Оригинал статьи: https://arxiv.org/pdf/2601.09999.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-18 07:24