Хвосты и Масштабирование: Что Движет Моделью Бергоми?

Автор: Денис Аветисян

Новое исследование показывает, что мультискалирование в модели Бергоми обусловлено, прежде всего, тяжелыми хвостами распределений доходностей, а не сложными временными зависимостями.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Зависимость прокси-функции мультимасштабирования [latex]B[/latex] от величины [latex]H[/latex] в модели Бергоми с шероховатостями демонстрирует характерное поведение, отражающее влияние негладкости на фрактальные свойства случайного процесса. — Зависимость прокси-функции мультимасштабирования $B$ от величины $H$ в модели Бергоми с шероховатостями демонстрирует характерное поведение, отражающее влияние негладкости на фрактальные свойства случайного процесса.

Мультискалирование в модели Бергоми является следствием стохастической волатильности и тяжелых хвостов, а не эффектов памяти.

Несмотря на широкое применение модели Rough Bergomi в финансовом моделировании, природа наблюдаемого в ней мультискалирования остается предметом дискуссий. В работе ‘Multiscaling in the Rough Bergomi Model: A Tale of Tails’ проведено исследование, направленное на выявление источника этого явления. Полученные результаты убедительно свидетельствуют о том, что мультискалирование в данной модели обусловлено преимущественно «толстыми хвостами» распределения доходностей, а не эффектами памяти. Может ли это означать, что акцент в построении моделей стохастической волатильности следует сместить с учета временной зависимости на анализ распределений доходностей?

По ту сторону стандартных моделей: Раскрытие сложности рыночной динамики

Традиционные финансовые модели, основанные на диффузионных процессах, зачастую оказываются неспособными адекватно отразить сложность динамики цен на активы. Эти модели, предполагающие постепенное и случайное изменение цен, не учитывают наблюдаемые на практике резкие скачки, длительные периоды стабильности и асимметричные колебания. В результате, предсказания, основанные на этих моделях, могут значительно отклоняться от реальных рыночных данных, особенно в периоды повышенной волатильности или кризисных ситуаций. Неспособность уловить всю палитру рыночного поведения обусловлена упрощенными предположениями о нормальном распределении доходностей и отсутствии долгосрочной памяти в ценовых рядах, что приводит к недооценке рисков и неэффективности стратегий управления активами. Наблюдаемая неадекватность стандартных моделей стимулирует поиск более сложных и реалистичных подходов к моделированию финансовых рынков.

Эмпирические данные последовательно демонстрируют, что волатильность на финансовых рынках не является случайным процессом, как это предполагается в классических моделях. Вместо этого наблюдаются периоды повышенной и пониженной волатильности, формирующие так называемые кластеры волатильности, которые сохраняются на протяжении значительных отрезков времени. Кроме того, распределение доходности активов часто отклоняется от нормального закона, характеризуясь более “тяжелыми хвостами” и выраженной асимметрией. Эти отклонения указывают на то, что стандартные предположения о нормальном распределении и постоянной волатильности не отражают реальную динамику рынков. Наблюдаемые закономерности намекают на наличие скрытых механизмов, таких как долгосрочная зависимость, нелинейные эффекты или влияние внешних факторов, которые необходимо учитывать для более точного моделирования и прогнозирования поведения финансовых активов. $\sigma_t = \sqrt{GARCH(p,q)}$ — подобная структура, учитывающая прошлую волатильность, может быть необходима для адекватного описания наблюдаемых явлений.

Несоответствие между предсказаниями стандартных финансовых моделей и реальной динамикой цен на активы требует изучения явлений мультискалирования. Данный феномен предполагает, что изменения цен демонстрируют различную динамику на разных временных масштабах — от краткосрочных колебаний до долгосрочных трендов. Иными словами, волатильность и корреляции, наблюдаемые за короткий период, могут существенно отличаться от тех, что проявляются в более длительной перспективе. Исследование мультискалирования позволяет выявить закономерности, скрытые в структуре финансовых данных, и создать более точные модели, учитывающие неравномерность временных рядов. Понимание этих многоуровневых процессов критически важно для оценки рисков и разработки эффективных стратегий управления инвестициями, поскольку игнорирование мультискалирования может приводить к существенным ошибкам в прогнозировании и, как следствие, к финансовым потерям.

Уменьшение параметра HH в модели Rough Bergomi приводит к увеличению нерегулярности траекторий цен, утяжелению распределений доходностей и усилению кластеризации и шероховатости волатильности.

Модель Rough Bergomi: Новый взгляд на волатильность

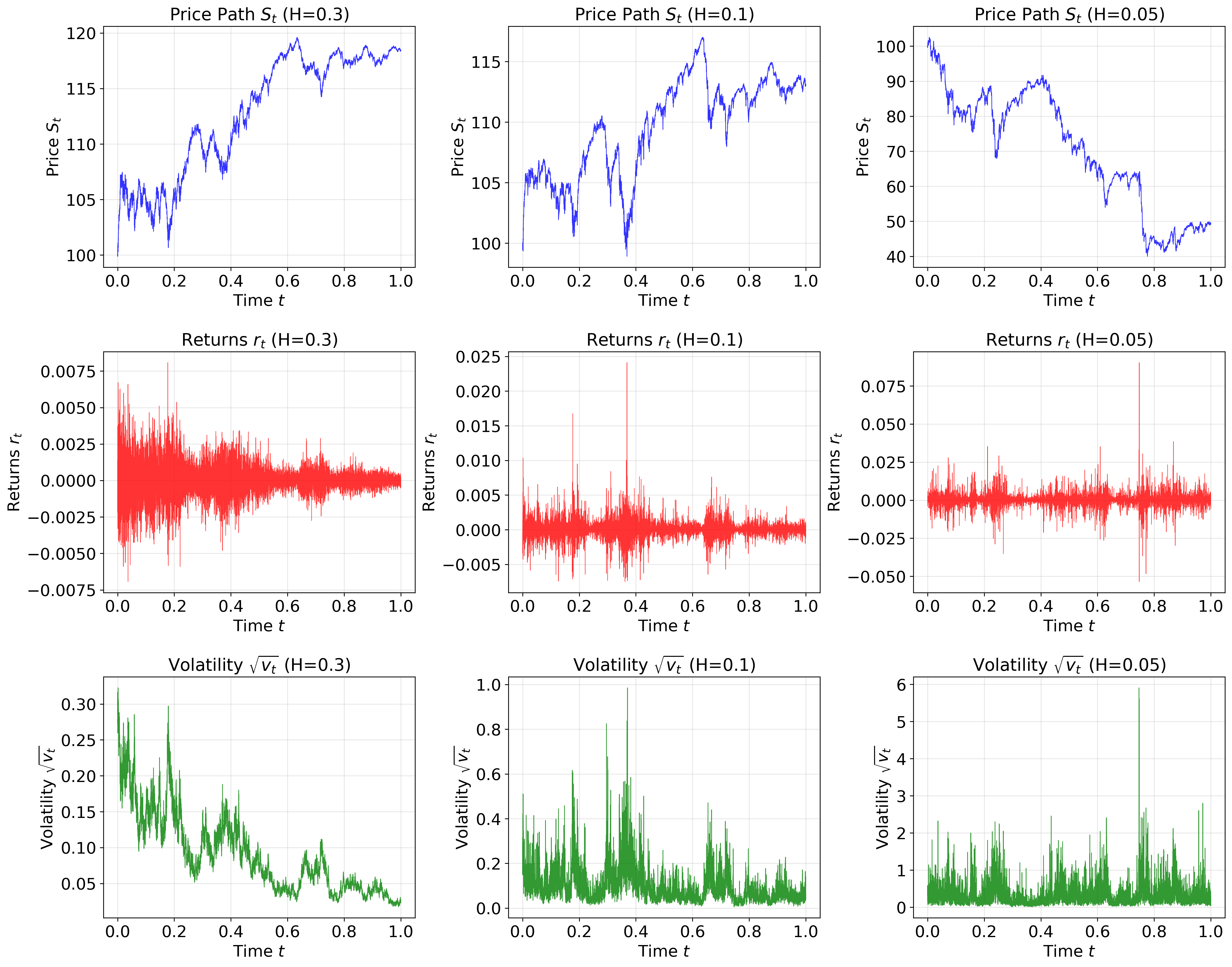
Модель Rough Bergomi представляет собой продвинутый подход к моделированию финансовых временных рядов, использующий фрактальное броуновское движение для генерации реалистичных траекторий волатильности. В отличие от стандартных моделей, предполагающих независимые приращения, фрактальное броуновское движение характеризуется зависимостью приращений во времени, что позволяет моделировать долгосрочные зависимости и нерегулярности, наблюдаемые на финансовых рынках. Это достигается за счет использования параметра Херста $H$ , определяющего степень самоподобия и долгосрочной памяти процесса. Модель позволяет генерировать более правдоподобные траектории волатильности, чем традиционные модели, такие как Black-Scholes, что особенно важно для оценки и хеджирования сложных деривативов и управления рисками.

Включение концепции «шероховатости» (roughness) в модель позволяет более адекватно отразить характеристики реальных финансовых рынков, проявляющиеся в долгосрочной зависимости и нерегулярности временных рядов. Традиционные модели часто предполагают независимость изменений цен, что не соответствует наблюдаемым паттернам, где корреляции сохраняются на протяжении значительных периодов времени. Шероховатость, достигаемая за счет использования дробного броуновского движения, моделирует эти долгосрочные зависимости, учитывая, что текущая волатильность зависит от её предыдущих значений на протяжении длительного времени. Это приводит к более реалистичному моделированию волатильности и, как следствие, к более точным оценкам рисков и ценообразованию деривативов. Фактически, модель позволяет уловить «память» волатильности, что особенно важно для анализа рыночных шоков и экстремальных событий.

Зависимость модели от показателя Херста (Hurst exponent) позволяет количественно оценить “память” волатильности и ее влияние на динамику цен. Показатель Херста, принимающий значения от 0 до 1, определяет степень долгосрочной зависимости в траекториях волатильности. Значение, близкое к 0, указывает на отсутствие памяти и случайный характер изменений волатильности. Значение, приближающееся к 1, указывает на сильную долгосрочную зависимость, где волатильность имеет тенденцию сохранять свое направление. В модели Rough Bergomi, значение показателя Херста $H \in (0, 1)$ напрямую влияет на характеристики фрактальной случайной траектории, определяющей динамику волатильности, и, следовательно, на расчет ценовых траекторий.

В модели rough Bergomi наблюдается выраженная волатильность, усиливающаяся с ростом параметра Херста [latex]H[/latex], что проявляется в увеличении суммы первых 10 автокорреляционных коэффициентов абсолютных доходностей от почти нуля при [latex]H\leq 0.01[/latex] до приблизительно 3 при [latex]H=0.2[/latex], согласно 1000 независимым симуляциям. — В модели rough Bergomi наблюдается выраженная волатильность, усиливающаяся с ростом параметра Херста $H$ , что проявляется в увеличении суммы первых 10 автокорреляционных коэффициентов абсолютных доходностей от почти нуля при $H\leq 0.01$ до приблизительно 3 при $H=0.2$ , согласно 1000 независимым симуляциям.

Подтверждение мультискалирования: Синтетические и статистические тесты

Для подтверждения наличия мультискалирования в финансовых данных используется модель Multifractal Random Walk — синтетическая модель, специально разработанная для демонстрации данного свойства. Эта модель позволяет генерировать временные ряды, обладающие характеристиками мультискалирования, что служит эталоном для сравнения с реальными финансовыми данными. Использование синтетической модели позволяет отделить истинное мультискалирование от случайных флуктуаций и статистических артефактов, возникающих при анализе реальных данных, поскольку все параметры модели известны и контролируются. Данный подход обеспечивает возможность валидации методов обнаружения мультискалирования и оценки их чувствительности и точности.

Для верификации наличия мультискалирования и исключения ложных срабатываний, вызванных статистическими артефактами, применяется анализ на основе суррогатных данных. Данный подход включает в себя два основных метода: создание перемешанных суррогатов (shuffled surrogates), которые сохраняют распределение исходных данных, но разрушают временную корреляцию, и генерацию согласованных фрактальных движений Брауна (matched fractional Brownian motion), имитирующих долгосрочные зависимости, но не обладающих характеристиками мультискалирования. Сравнение статистических характеристик исходных данных с характеристиками, полученными для суррогатных данных, позволяет оценить, насколько наблюдаемое мультискалирование является реальным свойством данных, а не результатом случайных флуктуаций или особенностей статистического распределения.

В ходе проведенного исследования установлено, что при значениях параметра шероховатости (H) менее 0.01, 100% проведенных симуляций демонстрируют выраженное мультискалирование. Это указывает на высокую вероятность возникновения мультискалирующего поведения в моделях, настроенных на столь низкие значения параметра шероховатости, и подтверждает, что данный параметр является ключевым фактором, определяющим наличие данного свойства в синтетических данных. Полученные результаты позволяют использовать модели с H < 0.01 в качестве эталонных для валидации мультискалирования в реальных финансовых данных.

Анализ распределительных свойств временных рядов выявил, что подавляющая доля (95.3%) наблюдаемого мультискалирования обусловлена именно характеристиками распределения данных, а не их временной структурой. Лишь 4.7% наблюдаемого эффекта мультискалирования связано с временными свойствами рядов. Данный результат указывает на преобладающую роль статистических характеристик данных в формировании мультискалирующего поведения, что необходимо учитывать при построении и интерпретации моделей финансовой динамики и анализе рисков.

Обобщенный показатель Херста (Generalized Hurst Exponent) является ключевым метриком для количественной оценки степени мультискалирования, наблюдаемого как в смоделированных, так и в реальных финансовых данных. Значение этого показателя позволяет определить преобладание долгосрочных зависимостей и фрактальное поведение временных рядов. В частности, отклонения от значения 0.5 указывают на наличие долгосрочных зависимостей: значения больше 0.5 свидетельствуют о персистентности (тенденции к продолжению тренда), а значения меньше 0.5 — об антиперсистентности (тенденции к развороту тренда). $H$ рассчитывается на основе анализа масштабируемости дисперсии временного ряда и предоставляет объективную меру степени мультискалирования, позволяя сравнивать различные наборы данных и модели.

В модели Бергоми с шероховатостью, увеличение параметра Херста [latex]H[/latex] приводит к значительному снижению тяжести хвостов распределения доходности, при этом медианные значения уменьшаются от примерно 50 для сильно шероховатых процессов ([latex]H=0.001[/latex]) до около 5 при [latex]H=0.2[/latex], что подтверждено 1000 независимыми симуляциями. — В модели Бергоми с шероховатостью, увеличение параметра Херста $H$ приводит к значительному снижению тяжести хвостов распределения доходности, при этом медианные значения уменьшаются от примерно 50 для сильно шероховатых процессов ( $H=0.001$ ) до около 5 при $H=0.2$ , что подтверждено 1000 независимыми симуляциями.

Влияние на экстремальные события и устойчивость модели

Модель Rough Bergomi, благодаря генерации динамики, соответствующей мультискалированию, естественным образом формирует распределения с “тяжелыми хвостами”. Это означает, что вероятность наступления экстремальных событий, таких как резкие скачки или падения активов, значительно выше, чем в традиционных моделях, предполагающих нормальное распределение. В отличие от последних, где подобные события считаются крайне редкими, модель Rough Bergomi адекватно описывает реальные финансовые данные, где экстремальные колебания происходят заметно чаще. Такое поведение связано с тем, что мультискалирование позволяет модели захватывать сложные зависимости в данных и учитывать влияние событий разных масштабов, что, в свою очередь, приводит к увеличению вероятности возникновения неожиданных и значительных изменений в ценах активов. $\text{Это особенно важно для оценки рисков и управления портфелем}$ .

Куртозис, как мера «толщины хвостов» распределения, предоставляет количественную связь между результатами модели и наблюдаемым распределением доходности активов. В частности, при значении параметра Херста $H = 0.001$ , модель демонстрирует значения куртозиса, приближающиеся к 50. Это указывает на значительно более высокую вероятность экстремальных событий, чем предполагает нормальное распределение, и подтверждает способность модели адекватно отражать реальную динамику финансовых рынков, характеризующуюся повышенной вероятностью резких скачков и падений. Высокий куртозис, таким образом, служит важным индикатором точности модели в прогнозировании рисков, связанных с редкими, но значительными колебаниями цен.

Исследования показали, что при увеличении параметра Херста до значения 0.2, эксцесс, являющийся мерой “толщины хвостов” распределения, снижается приблизительно до 5. Это указывает на уменьшение вероятности экстремальных событий и более умеренное поведение активов. В то время как низкие значения параметра Херста (например, 0.001) приводят к значительному эксцессу, около 50, что свидетельствует о выраженной склонности к резким колебаниям, увеличение Херста сглаживает распределение, приближая его к нормальному и снижая риск непредсказуемых скачков. Данное изменение эксцесса демонстрирует способность модели адаптироваться к различным уровням долгосрочной зависимости и тяжести хвостов, предлагая более гибкий инструмент для моделирования финансовых рынков.

Дополнительное тестирование с использованием фрактального левиевского стабильного движения подтвердило устойчивость модели Rough Bergomi при работе как с долгосрочной зависимостью, так и с тяжелыми хвостами распределений. Данный подход позволяет адекватно моделировать финансовые активы, демонстрирующие не только тенденцию к сохранению ценовых движений на протяжении длительного времени, но и повышенную вероятность экстремальных событий. Подтверждена способность модели корректно отражать как тенденцию к кластеризации убытков, так и наличие значительных скачков цен, что особенно важно для оценки рисков и разработки эффективных стратегий управления активами. Результаты демонстрируют, что модель сохраняет свою адекватность даже при наличии сложных зависимостей и ненормальных распределений, что делает ее ценным инструментом для анализа финансовых рынков.

Исследование демонстрирует, что наблюдаемое мультискалирование в модели rough Bergomi в первую очередь обусловлено распределениями возвратов с «тяжелыми хвостами», возникающими в результате стохастической волатильности. Этот вывод подчеркивает важность понимания влияния волатильности на финансовые модели. Как заметил Поль Фейерабенд: «В науке нет универсального метода, а есть лишь набор уловок». В данном случае, кажущаяся сложность мультискалирования оказывается иллюзией, вызванной не сложными временными зависимостями, а базовой характеристикой волатильности. Анализ фокусируется не на добавлении сложности, а на выявлении фундаментальных причин наблюдаемого явления — именно в этом проявляется истинный смысл моделирования.

Что Дальше?

Представленная работа, лишая сложность кажущейся многомасштабности в модели Бергоми, обнажает простую истину: тяжелые хвосты распределений возвратов, порожденные стохастической волатильностью, оказываются достаточным объяснением наблюдаемого феномена. Бессмысленно искать призрачные зависимости во времени, когда причина кроется в фундаментальной природе волатильности. Система, требующая сложного аппарата для объяснения очевидного — проиграла.

Тем не менее, отказ от многомасштабного анализа не означает полного исчерпания вопроса. Понимание механизмов генерации тяжелых хвостов — задача, далекая от завершения. Будущие исследования должны сосредоточиться на более реалистичных моделях стохастической волатильности, учитывающих не только распределение, но и динамику самих изменений волатильности. Понятность — это вежливость; избегайте усложнения ради усложнения.

Особый интерес представляет вопрос о границах применимости упрощенных моделей. Когда упрощение становится искажением реальности? Ответ на этот вопрос потребует не только математической строгости, но и честной оценки практической значимости полученных результатов. Не стоит забывать, что идеальная модель — это не та, которая идеально описывает данные, а та, которая позволяет предсказывать будущее с минимальными усилиями.

Оригинал статьи: https://arxiv.org/pdf/2601.11305.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-19 10:17