Оптимизация знаний из разных источников: новый подход к машинному обучению

Автор: Денис Аветисян

Исследование предлагает теоретическую основу и практический алгоритм для эффективного использования данных из множества источников в задачах переноса обучения.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал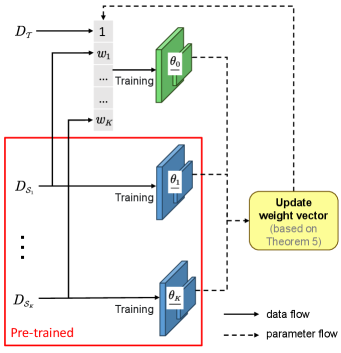

Обучающая схема UOWQ использует итеративный процесс, в котором параметры модели оптимизируются посредством градиентного спуска с использованием целевых данных и взвешенных выборок из каждой исходной задачи, при этом веса исходных задач обновляются на основе текущих параметров модели, формируя таким образом замкнутый цикл, совместно оптимизирующий веса источников и целевую модель.

Предложена унифицированная оптимизация весов источников и количеств переноса в многоисточниковом обучении с использованием асимптотического анализа.

Несмотря на широкое применение, перенос обучения из множества источников часто страдает от негативного переноса, требуя взвешенного подхода к вкладу каждого источника. В работе, озаглавленной ‘Unified Optimization of Source Weights and Transfer Quantities in Multi-Source Transfer Learning: An Asymptotic Framework’, предложен теоретический каркас UOWQ, формулирующий задачу переноса обучения как проблему оценки параметров на основе асимптотического анализа расхождения Кульбака-Лейблера. Ключевым результатом является доказательство оптимальности использования всех доступных данных из источников при корректной настройке весов, а также разработка эффективных алгоритмов для определения этих весов и количества переносимых данных. Не приведет ли предложенный подход к существенному улучшению производительности моделей в условиях ограниченных данных и позволит ли он более эффективно использовать гетерогенные источники знаний?

Истинная Природа Переноса Обучения: Вызов Смещения Домена

Перенос обучения, будучи перспективным подходом в машинном обучении, направлен на использование знаний, полученных при решении одной задачи, для повышения эффективности при решении другой. Однако, на практике, производительность таких систем часто снижается при столкновении с проблемой смещения домена — различиями в распределении данных между исходной и целевой областями. Это явление, известное как негативный перенос, возникает из-за того, что модель, обученная на одном наборе данных, может оказаться неспособной эффективно обобщать знания на данные, существенно отличающиеся по своим характеристикам. Несмотря на теоретическую привлекательность переноса обучения, преодоление смещения домена остается ключевой задачей для обеспечения его надежной работы в реальных приложениях и раскрытия всего потенциала данного подхода.

Снижение эффективности, часто проявляющееся как негативный перенос знаний, возникает из-за различий в пространствах признаков исходной и целевой областей. Представьте, что алгоритм обучен распознавать объекты на фотографиях, сделанных в хорошем освещении, а затем применяется к изображениям, полученным в условиях низкой освещенности или с другого типа камеры. Различия в распределении признаков — например, яркости, контрастности, текстуры — приводят к тому, что модель, хорошо работавшая в исходной области, начинает ошибаться в новой. Эти расхождения могут быть вызваны различными факторами, включая различия в датчиках, условиях съемки, или даже способе представления данных. Преодоление этих несоответствий в пространствах признаков является ключевой задачей для успешного применения переноса обучения в реальных условиях и избежания негативного переноса, когда знания из исходной области, напротив, ухудшают производительность в целевой.

Существующие методы переноса обучения часто демонстрируют ограниченную эффективность при столкновении с изменениями в данных, известных как смещение домена. Неспособность адаптироваться к различиям в распределении признаков между исходным и целевым доменами приводит к снижению обобщающей способности модели и, как следствие, к ухудшению производительности. Это особенно заметно в реальных приложениях, где данные могут значительно отличаться от тех, на которых модель была изначально обучена. В результате, потенциал переноса обучения для решения практических задач остается не полностью реализованным, поскольку модели, успешно работающие в лабораторных условиях, могут давать неудовлетворительные результаты при развертывании в реальном мире. Необходимость разработки более надежных и адаптивных методов, способных преодолевать смещение домена, является ключевой задачей для дальнейшего развития области переноса обучения.

Реализация полного потенциала переноса обучения в практических приложениях напрямую зависит от эффективного преодоления проблемы смещения доменов. Несоответствие между распределениями данных в исходном и целевом доменах часто приводит к ухудшению производительности, нивелируя преимущества, которые могло бы обеспечить использование предварительно обученных моделей. Успешное решение этой задачи позволит создавать системы, способные адаптироваться к новым условиям и данным без существенной потери точности, открывая возможности для широкого спектра применений — от обработки естественного языка и компьютерного зрения до робототехники и медицинского анализа. В конечном итоге, преодоление смещения доменов является ключевым фактором для превращения переноса обучения из многообещающей концепции в надежный и эффективный инструмент для решения реальных задач.

Набор данных, включающий DomainNet и OfficeHome, демонстрирует разнообразие визуальных стилей и условий съемки, характерные для изображений из различных доменов.

UOWQ: Формальный Подход к Оптимизации Мульти-Источникного Переноса

Многозадачное обучение с переносом (multi-source transfer learning) представляет собой перспективное решение для повышения эффективности обучения, позволяющее объединять знания, полученные из различных исходных задач. Однако, эффективная комбинация этих источников знаний представляет собой сложную проблему. Традиционные методы часто сталкиваются с трудностями при определении релевантности и веса каждого исходного домена, что может привести к негативному переносу знаний и снижению производительности. Проблема усугубляется различиями в распределениях данных между исходными и целевыми задачами, а также необходимостью выбора оптимального способа агрегации знаний из различных источников для максимизации обобщающей способности модели на целевой задаче.

Фреймворк UOWQ представляет собой новый подход к совместной оптимизации весов источников и объемов переносимого знания, основанный на асимптотическом анализе. В рамках данного подхода, веса источников и объемы переносимого знания определяются как функции от параметров модели, стремящихся к определенным асимптотическим значениям. Это позволяет аналитически вывести оптимальные значения весов и объемов, минимизируя ошибку обобщения на целевой задаче. Оптимизация производится путем поиска таких весов и объемов, которые обеспечивают максимальную информативность переносимого знания при минимальных затратах на передачу, что позволяет повысить эффективность обучения модели на целевой задаче. Асимптотический анализ позволяет избежать вычислительно сложных операций, связанных с непосредственной оптимизацией на конечных данных.

В рамках UOWQ, количественная оценка информативности каждой исходной задачи осуществляется посредством использования матрицы Фишера $F$ . Эта матрица, представляющая собой ожидаемое значение квадрата второго порядка частной производной логарифмической функции правдоподобия, служит мерой количества информации, содержащейся в градиентах параметров модели, полученных при обучении на конкретной исходной задаче. Более высокие значения элементов матрицы $F$ указывают на более значимую и информативную задачу. UOWQ использует эти значения для взвешивания вклада каждой исходной задачи в процесс переноса обучения, отбирая наиболее релевантные знания и минимизируя влияние задач с низкой информативностью, что способствует повышению обобщающей способности модели на целевой задаче.

Фреймворк UOWQ обеспечивает более принципиальный и эффективный перенос знаний, что приводит к улучшению обобщающей способности на целевых задачах. Оптимизация весов источников и количества переносимой информации, основанная на асимптотическом анализе и матрице Фишера, позволяет выявлять наиболее релевантные знания из множества исходных задач. Это, в свою очередь, снижает влияние нерелевантных или избыточных данных, что способствует повышению точности и надежности модели на новых, ранее не встречавшихся данных. Практические результаты демонстрируют, что UOWQ превосходит существующие методы переноса знаний по ключевым показателям обобщающей способности, особенно в условиях ограниченного количества данных для целевой задачи.

Изменение веса передачи [latex]w_1[/latex] влияет на смещение и дисперсию оценки: увеличение [latex]w_1[/latex] снижает дисперсию и увеличивает смещение при [latex]w_1 \in [0, 1][/latex], но увеличивает и то, и другое при [latex]w_1 \in (1, +\in fty)[/latex], при этом оптимальное значение [latex]w_1^*[/latex] обеспечивает наилучший компромисс между ними. — Изменение веса передачи $w_1$ влияет на смещение и дисперсию оценки: увеличение $w_1$ снижает дисперсию и увеличивает смещение при $w_1 \in [0, 1]$ , но увеличивает и то, и другое при $w_1 \in (1, +\in fty)$ , при этом оптимальное значение $w_1^*$ обеспечивает наилучший компромисс между ними.

Экспериментальная Проверка и Достигнутые Результаты

Методика UOWQ подверглась строгой оценке на широко известных наборах данных Office-Home и DomainNet, которые специально разработаны для оценки производительности моделей машинного обучения в условиях значительных изменений домена (domain shift). Набор данных Office-Home включает изображения, полученные из офисных и домашних сцен, а DomainNet состоит из изображений, охватывающих шесть различных доменов: изображения, нарисованные от руки (Quickdraw), картины (Painting), фотографии, нарисованные цифровым способом (Sketch), изображения из реального мира (Real World), инфляционные фотографии и изображения, полученные с помощью синтетического рендеринга. Использование этих наборов данных позволило всесторонне оценить способность UOWQ к обобщению и адаптации к новым, ранее не встречавшимся условиям съемки и стилю изображений.

В ходе экспериментов для оценки UOWQ использовались две архитектуры нейронных сетей: ResNet-18 и ViT-Small. Обе модели обучались с применением оптимизатора Adam, что позволило обеспечить стабильность и эффективность процесса обучения. Выбор данных архитектур позволил оценить универсальность UOWQ, поскольку ResNet-18 представляет собой сверточную нейронную сеть, а ViT-Small — трансформерную модель, использующую механизм внимания. Применение Adam позволило автоматически адаптировать скорость обучения для каждого параметра модели, оптимизируя процесс сходимости и улучшая общую производительность.

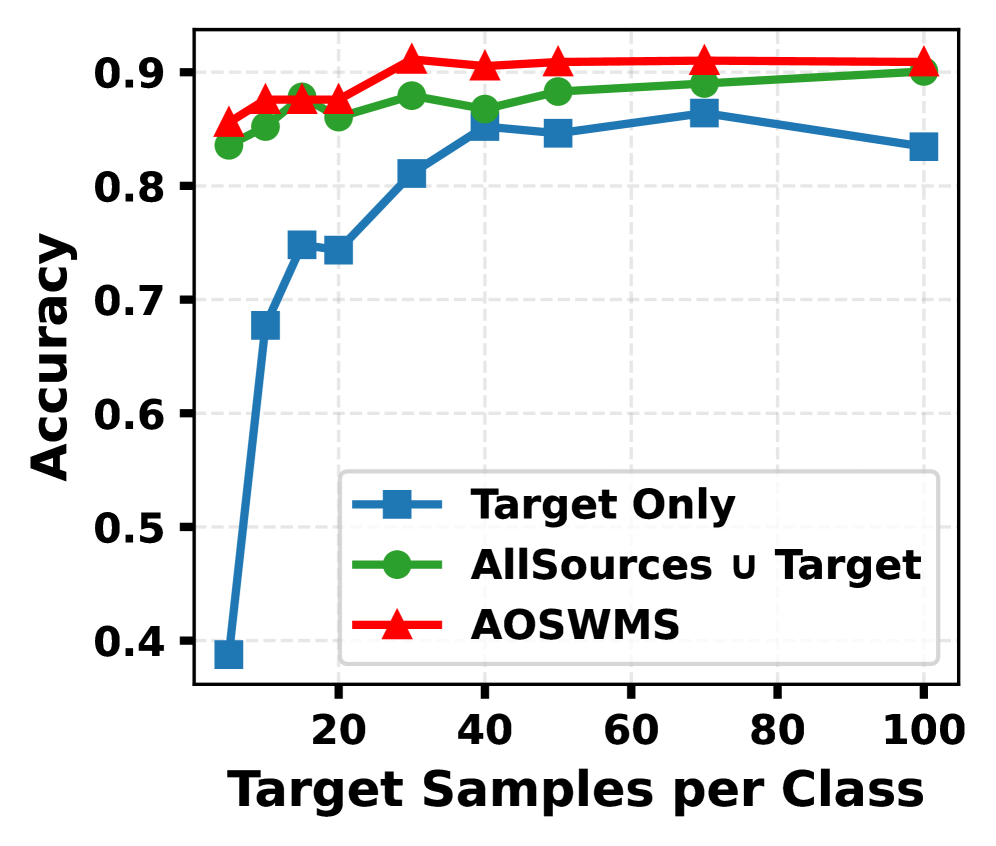
В ходе экспериментов на наборах данных Office-Home и DomainNet, UOWQ демонстрирует стабильное превосходство над существующими методами. Средняя точность UOWQ составила 51.9% на DomainNet и 79.1% на Office-Home. Данный подход превзошел наиболее эффективную базовую модель (MoDo) на 0.7 и 0.4 процентных пункта соответственно, что подтверждает его эффективность в задачах адаптации к различным доменам.

В ходе экспериментов на датасетах DomainNet и Office-Home, UOWQ продемонстрировал значительное улучшение точности на отдельных задачах. На задаче Quickdraw датасета DomainNet, UOWQ достиг абсолютной точности 36.8%, что на 3.0% выше, чем у предыдущего лучшего результата. Аналогично, на задаче Painting в DomainNet, точность составила 35.2%, что на 1.4% превосходит предыдущий показатель. В датасете Office-Home, UOWQ показал улучшение на 0.8% на задаче Art и на 0.4% на задаче Real World, подтверждая эффективность подхода на различных типах данных.

В основе UOWQ лежит применение асимптотического анализа и расхождения Кульбака-Лейблера (Kullback-Leibler Divergence, $D_{KL}[P||Q]$ ), что позволяет повысить надежность и устойчивость процесса переноса обучения. Асимптотический анализ используется для оценки поведения модели при увеличении объема данных, выявляя ключевые факторы, влияющие на обобщающую способность. Расхождение Кульбака-Лейблера, в свою очередь, служит метрикой для измерения различий между распределениями исходной и целевой областей, минимизируя отклонения и обеспечивая более эффективный перенос знаний. Комбинация этих методов способствует снижению чувствительности к изменениям в данных и повышению адаптивности модели к новым, ранее не встречавшимся условиям.

Результаты на наборе данных Office-Home демонстрируют, что производительность системы изменяется в зависимости от количества целевых снимков.

Значение и Перспективы Развития

Предлагаемый подход UOWQ представляет собой обоснованную методику смягчения негативного влияния смещения домена в процессе переноса обучения, что позволяет создавать более устойчивые и надежные модели. В отличие от эмпирических методов, UOWQ формально учитывает расхождения между исходным и целевым доменами, оптимизируя как веса исходной модели, так и количество передаваемой информации. Это обеспечивает адаптацию знаний к новым задачам с повышенной эффективностью и уменьшением риска переобучения. Благодаря такому принципиальному подходу, модели, обученные с использованием UOWQ, демонстрируют улучшенную обобщающую способность и стабильность в условиях, когда распределения данных в обучающей и тестовой выборках существенно различаются, что крайне важно для практического применения машинного обучения в реальных сценариях.

Предлагаемый фреймворк демонстрирует значительный потенциал в адаптации знаний между различными задачами благодаря одновременной оптимизации как весов исходной модели, так и объемов переносимой информации. Вместо того, чтобы полагаться исключительно на настройку весов или на выбор оптимальных признаков для переноса, система динамически регулирует оба этих аспекта. Такой подход позволяет более эффективно использовать знания, полученные на исходной задаче, и минимизировать негативное влияние различий между доменами. В результате, модель способна адаптироваться к новым задачам с меньшими затратами вычислительных ресурсов и достигать более высокой производительности по сравнению с традиционными методами трансферного обучения. Гибкость и точность этой оптимизации открывают новые возможности для применения в широком спектре задач машинного обучения, где необходимо эффективно использовать существующие знания для решения новых проблем.

Дальнейшие исследования направлены на расширение возможностей UOWQ для решения более сложных сценариев смещения доменов, включая ситуации, когда различия между исходным и целевым доменами значительно возрастают. Особое внимание будет уделено адаптации алгоритма к задачам, требующим учета не только изменений в распределении данных, но и структурных различий между доменами. Кроме того, планируется изучить применимость UOWQ в различных парадигмах машинного обучения, таких как обучение с подкреплением и генеративные модели, с целью повышения их устойчивости к изменениям в окружающей среде и улучшения обобщающей способности. Предполагается, что расширение области применения UOWQ позволит создать более гибкие и надежные системы искусственного интеллекта, способные эффективно адаптироваться к новым условиям и решать широкий спектр задач.

Данное исследование вносит значительный вклад в развитие более эффективных и обобщенных систем машинного обучения, открывая новые возможности для прогресса в различных областях. Благодаря способности адаптировать знания к новым задачам и условиям, разработанный подход позволяет создавать модели, менее подверженные влиянию изменений в данных. Это особенно важно для практических приложений, где данные часто отличаются от тех, на которых обучалась модель. Перспективные направления включают автоматизацию процесса адаптации и расширение применимости к более сложным типам данных и задачам, что в конечном итоге позволит создавать интеллектуальные системы, способные к самообучению и адаптации в динамично меняющемся мире.

Представленная работа демонстрирует, что совместная оптимизация весов источников и величин переноса данных позволяет добиться значительного улучшения в задачах многоисточного трансферного обучения, особенно при ограниченном количестве обучающих примеров. Это согласуется с глубокой убежденностью Алана Тьюринга: “Я не думаю, что когда-нибудь можно будет сказать, что машина «думает» так же, как человек, но я думаю, что мы можем сделать так, чтобы машины вели себя так, как будто они думают.”. В данном контексте, тщательно выверенная математическая модель, предложенная авторами, позволяет «заставить» алгоритм эффективно использовать информацию из различных источников, приближая его поведение к оптимальному решению даже в условиях неполноты данных. Анализ расхождений Кульбака-Лейблера, лежащий в основе предложенного подхода, подчеркивает стремление к математической чистоте и доказуемости, что является ключевым элементом элегантного и эффективного решения.

Куда двигаться дальше?

Представленная работа, хоть и демонстрирует элегантность совместной оптимизации весов источников и объемов переноса, не решает фундаментальную проблему: как определить истинную меру близости между доменами. Использование расхождения Кульбака-Лейблера — это прагматичный, но не всегда оправданный выбор. Если решение кажется магией — значит, инвариант не раскрыт. Следующим шагом видится разработка метрик, основанных на более глубоком понимании структуры данных, возможно, с привлечением инструментов дифференциальной геометрии или теории информации.

Ограничения асимптотического анализа также требуют внимания. Хотя доказательства корректности в пределе дают уверенность, практическая сходимость и устойчивость алгоритма в условиях ограниченных данных и вычислительных ресурсов — вопрос открытый. Необходимо исследовать влияние различных стратегий регуляризации и адаптивных методов оптимизации для повышения робастности и эффективности в реальных сценариях.

В конечном счёте, задача переноса знаний — это не только вопрос оптимизации, но и вопрос представления знаний. Следует задуматься о разработке более выразительных и компактных представлений, позволяющих эффективно переносить знания между доменами, минимизируя при этом риск переобучения и искажения информации. Истина, как всегда, кроется в простоте и математической строгости.

Оригинал статьи: https://arxiv.org/pdf/2601.10779.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-19 22:08