Опционные стратегии: новый подход к хеджированию в условиях высокой размерности

Автор: Денис Аветисян

Исследователи предложили эффективный метод хеджирования сложных опционов, основанный на применении Kolmogorov-Arnold Networks и глубокого обучения.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал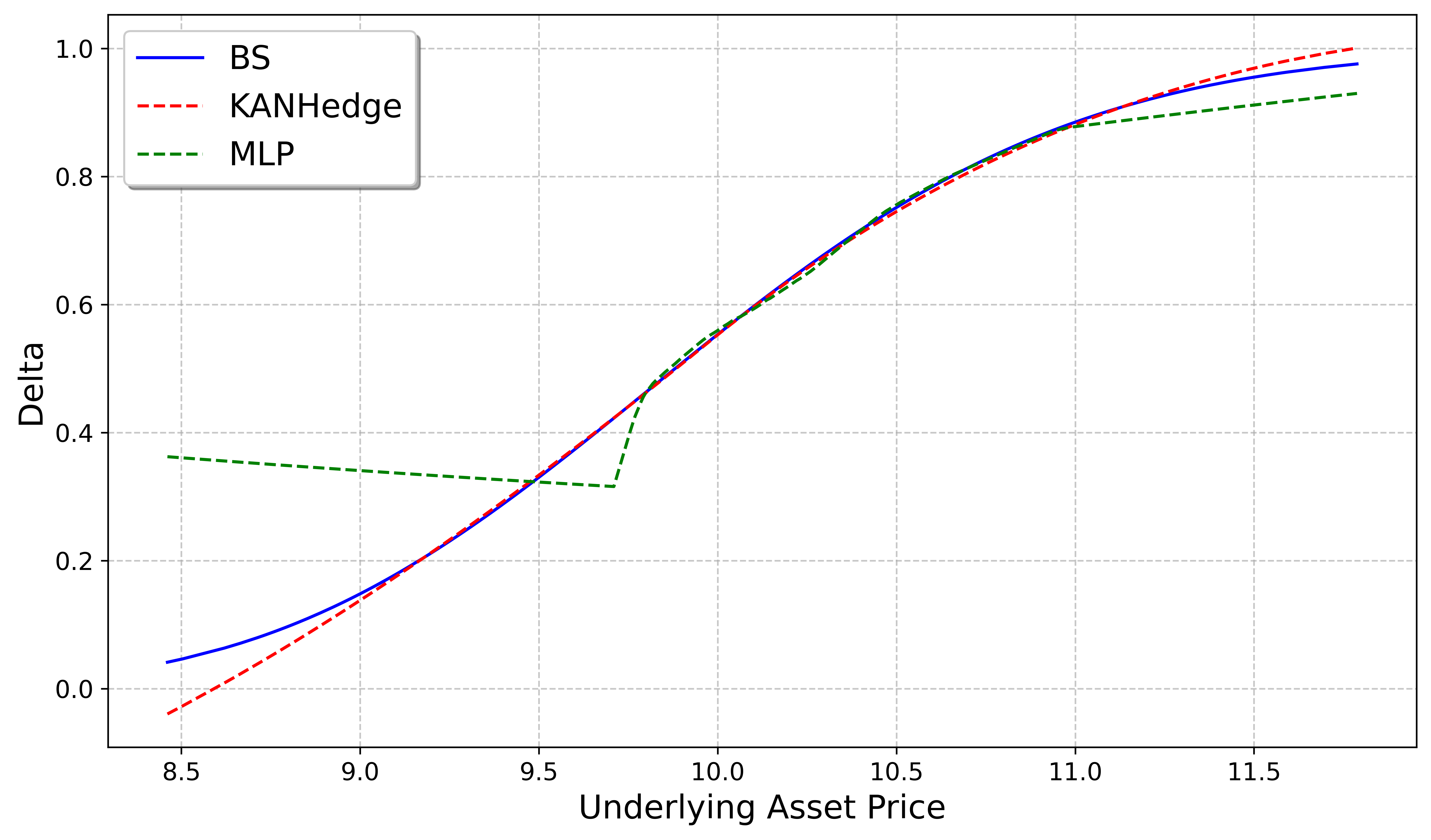

Для оценки дельты европейского колл-опциона в одномерном случае, метод KANHedge (обозначен красным) демонстрирует более точное приближение к аналитическому значению дельты, рассчитанному по формуле Блэка-Шоулза (синий), чем многослойный персептрон (зеленый), особенно в областях, где опцион находится «вне денег».

В статье представлена KANHedge — инновационная система, использующая сети Kolmogorov-Arnold в рамках Deep BSDE для повышения эффективности хеджирования корзин опционов высокой размерности.

Вычисление цен и формирование хеджа для опционов в многомерных пространствах представляет собой сложную задачу, ограничивающую эффективность традиционных численных методов. В данной работе, посвященной разработке ‘KANHedge: Efficient Hedging of High-Dimensional Options Using Kolmogorov-Arnold Network-Based BSDE Solver’, предлагается новый подход, использующий сети Колмогорова-Арнольда (KAN) в рамках решения обратных стохастических дифференциальных уравнений (BSDE). Полученные результаты демонстрируют, что KANHedge обеспечивает более точную оценку хеджа по сравнению с традиционными многослойными персептронами (MLP), сохраняя при этом сопоставимую точность ценообразования. Сможет ли предложенный метод стать стандартом де-факто для управления рисками в сложных финансовых инструментах?

Вызов многомерного ценообразования опционов

Традиционные методы оценки опционов, такие как уравнение Блэка-Шоулза $BS Equation$ , сталкиваются с серьезными ограничениями при работе с опционами на несколько базовых активов, известных как европейские корзинные опционы $European Basket Option$ . Проблема заключается в так называемом «проклятии размерности», когда вычислительная сложность и требуемые ресурсы экспоненциально возрастают с увеличением числа активов в корзине. Это происходит из-за необходимости учитывать все возможные комбинации изменений цен базовых активов, что делает точное и эффективное вычисление цены опциона практически невозможным при большом количестве составляющих. В результате, применение классической модели Блэка-Шоулза к сложным финансовым инструментам, включающим множество активов, становится непрактичным и требует поиска альтернативных, более эффективных подходов к оценке.

Существующие вычислительные методы, применяемые для оценки стоимости опционов на несколько базовых активов, сталкиваются со значительными ограничениями по мере увеличения их числа. С ростом размерности задачи, сложность вычислений возрастает экспоненциально, что приводит к неприемлемо высоким затратам времени и ресурсов. Например, методы Монте-Карло, часто используемые в финансовом моделировании, требуют огромного количества симуляций для достижения приемлемой точности при работе с большим количеством активов. Это, в свою очередь, делает их непрактичными для оценки сложных финансовых инструментов, таких как корзинные опционы на большое количество акций или опционы на процентные ставки, зависящие от множества макроэкономических факторов. В результате, традиционные подходы часто приводят к неточным оценкам, что снижает эффективность управления рисками и оптимизации портфеля, особенно в условиях динамично меняющихся финансовых рынков. $BS Equation$ и другие классические модели оказываются недостаточно эффективными для адекватного анализа таких инструментов.

Неспособность эффективно оценивать опционы на множество базовых активов серьезно ограничивает возможности точного управления рисками в современной финансовой практике. Неадекватная оценка стоимости сложных финансовых инструментов, таких как корзинные опционы, может привести к значительному занижению или завышению рисков, что, в свою очередь, негативно сказывается на процессах оптимизации портфеля. Инвесторы и финансовые институты, не имеющие доступа к надежным и быстрым методам ценообразования в условиях высокой размерности, сталкиваются с повышенной вероятностью убытков и упущенных возможностей. В результате, затрудняется адекватная оценка подверженности портфеля неблагоприятным колебаниям рыночной конъюнктуры и, следовательно, снижается общая эффективность инвестиционных стратегий. $BS Equation$ и традиционные подходы оказываются недостаточно эффективными, подчеркивая необходимость разработки инновационных вычислительных методов для преодоления данной проблемы.

При использовании риска убытков в качестве стоимости хеджирования, метод KANHedge (красный) демонстрирует незначительно лучшую эффективность по сравнению с MLP (зеленый) при хеджировании европейской геометрической корзины опционов.

Обратно-стохастические дифференциальные уравнения: основа ценообразования опционов

Обратно-стохастические дифференциальные уравнения (ОСУ) предоставляют эффективный инструмент для решения задач ценообразования опционов в многомерных пространствах, преобразуя их в задачи стохастической оптимизации. В отличие от традиционных методов, требующих решения сложных частных дифференциальных уравнений (ПДУ) в высоких размерностях, ОСУ позволяют выразить цену опциона как оптимальное управление стохастическим процессом. Это достигается путем формулировки задачи в терминах ожидаемого значения некоторой случайной величины, зависящей от траекторий базового актива и стратегии управления. Решение ОСУ, таким образом, соответствует оптимальной стратегии, минимизирующей (или максимизирующей) эту величину, что и приводит к определению справедливой цены опциона. $Y(t) = E[\xi | \mathcal{F}_t]$ , где $Y(t)$ — решение ОСУ в момент времени t, ξ — случайная величина, представляющая выплату по опциону в момент погашения, и $\mathcal{F}_t$ — фильтрация информации, доступной в момент времени t.

Теорема Фейнмана-Каца обеспечивает теоретическую основу для использования обратных стохастических дифференциальных уравнений (ОСДУ) в ценообразовании опционов, устанавливая связь между ОСДУ и частными дифференциальными уравнениями (ПДУ). В частности, теорема показывает, что решение ОСДУ с определенными терминальными и стохастическими условиями эквивалентно решению соответствующего ПДУ, известного как уравнение Колмогорова-Чаплыгина. Это позволяет применять хорошо разработанные численные методы для ПДУ, такие как метод конечных разностей или метод конечных элементов, для эффективного решения ОСДУ и, следовательно, для вычисления цен опционов в многомерных пространствах. Формально, если $Y_t$ является решением ОСДУ, а $f(x, t)[latex] - функцией, удовлетворяющей определенным условиям, то решение ПДУ [latex]\frac{\partial V}{\partial t} + \mathcal{L}V = 0$ с терминальным условием $V(T) = \xi$ может быть получено через $V(t) = E_t[ \xi ]$ , где $E_t$ - условное математическое ожидание при времени $t$ .

Непосредственное решение обратных стохастических дифференциальных уравнений (ОСДУ) требует значительных вычислительных ресурсов, особенно при работе со сложными производными финансовыми инструментами. Сложность обусловлена многомерностью пространства состояний и необходимостью численного решения уравнений в этом пространстве. Для повышения эффективности применяются различные методы, такие как методы Монте-Карло и конечно-разностные схемы, однако они всё равно могут быть ресурсоемкими при увеличении размерности и сложности производной. Вычислительная нагрузка возрастает экспоненциально с увеличением количества базовых активов и факторов, влияющих на стоимость опциона, что ограничивает применение прямого подхода к решению ОСДУ для высокоразмерных задач.

Глубокие BSDE: использование нейронных сетей для повышения эффективности

Методы глубоких BSDE используют многослойные персептроны (MLP) для параметризации величин, входящих в BSDE. Это позволяет эффективно аппроксимировать решения в задачах высокой размерности, где традиционные численные методы становятся вычислительно затратными. Параметризация включает в себя замену функций, определяющих решение BSDE, нейронной сетью, что сводит задачу к обучению этой сети на наборе данных. Такой подход позволяет получить приближенное решение BSDE без явного построения сетки или проведения итеративных вычислений, что особенно важно для задач, характеризующихся большим количеством факторов или сложной структурой.

Обучение нейронных сетей на сгенерированных данных позволяет точно оценивать стоимость сложных опционов без необходимости использования аналитических решений или ресурсоемких методов Монте-Карло. Вместо прямого вычисления стоимости, сеть аппроксимирует функцию стоимости на основе данных, полученных из симуляций, что значительно снижает вычислительную нагрузку. Этот подход особенно эффективен для опционов с высокой размерностью и сложными зависимостями, где традиционные методы становятся непрактичными из-за экспоненциального роста вычислительных затрат. Точность оценки напрямую зависит от объема и качества обучающих данных, а также от архитектуры и параметров используемой нейронной сети.

Использование глубоких BSDE значительно снижает вычислительную нагрузку при ценообразовании финансовых инструментов. Традиционные методы, такие как Монте-Карло симуляции, требуют значительных ресурсов для достижения приемлемой точности, особенно в задачах высокой размерности. В отличие от них, параметризация компонентов BSDE с помощью нейронных сетей позволяет аппроксимировать решения, используя значительно меньше вычислительных ресурсов. Это расширяет возможности точного ценообразования для сложных финансовых деривативов, включая экзотические опционы и инструменты со сложными зависимостями, которые ранее были непрактичны для оценки с использованием стандартных методов.

KANHedge: новый подход с использованием сетей Колмогорова-Арнольда

KANHedge представляет собой новый подход к решению задач ценообразования и хеджирования опционов в многомерных пространствах, основанный на использовании сетей Колмогорова-Арнольда (KAN). В отличие от традиционных методов глубокого обучения, таких как Deep BSDE, KANHedge использует архитектуру KAN для повышения эффективности моделирования сложных финансовых инструментов. KAN позволяют эффективно аппроксимировать функции в высоких размерностях, что особенно важно при работе с корзинами опционов и другими производными финансовыми инструментами, требующими учета множества базовых активов. Это позволяет расширить возможности Deep BSDE и решать более сложные задачи ценообразования и управления рисками.

В архитектуре KANHedge используются обучаемые функции активации, основанные на B-сплайнах ( $BSpline$ ), что обеспечивает улучшенное моделирование непрерывных функций по сравнению с традиционными многослойными перцептронами (MLP). В отличие от MLP, использующих фиксированные функции активации, такие как ReLU или сигмоида, B-сплайны позволяют KAN более гибко аппроксимировать сложные функции, особенно в задачах опционного ценообразования. Обучаемость параметров B-сплайнов позволяет сети адаптироваться к специфике решаемой задачи, что приводит к повышению точности и эффективности моделирования по сравнению со статичными функциями активации, применяемыми в MLP.

Применение KANHedge обеспечивает более точное и эффективное ценообразование сложных производных финансовых инструментов, включая опционы на корзину активов американского и геометрического типа, а также позволяет разрабатывать надежные стратегии хеджирования. В ходе тестирования KANHedge продемонстрировал снижение стоимости хеджирования до 9% (измеряемого как CVaR) по сравнению с методами на основе многослойных персептронов (MLP), при этом погрешность ценообразования оставалась в пределах 1%. Данные результаты подтверждают преимущества использования KANHedge для управления рисками и оптимизации портфелей.

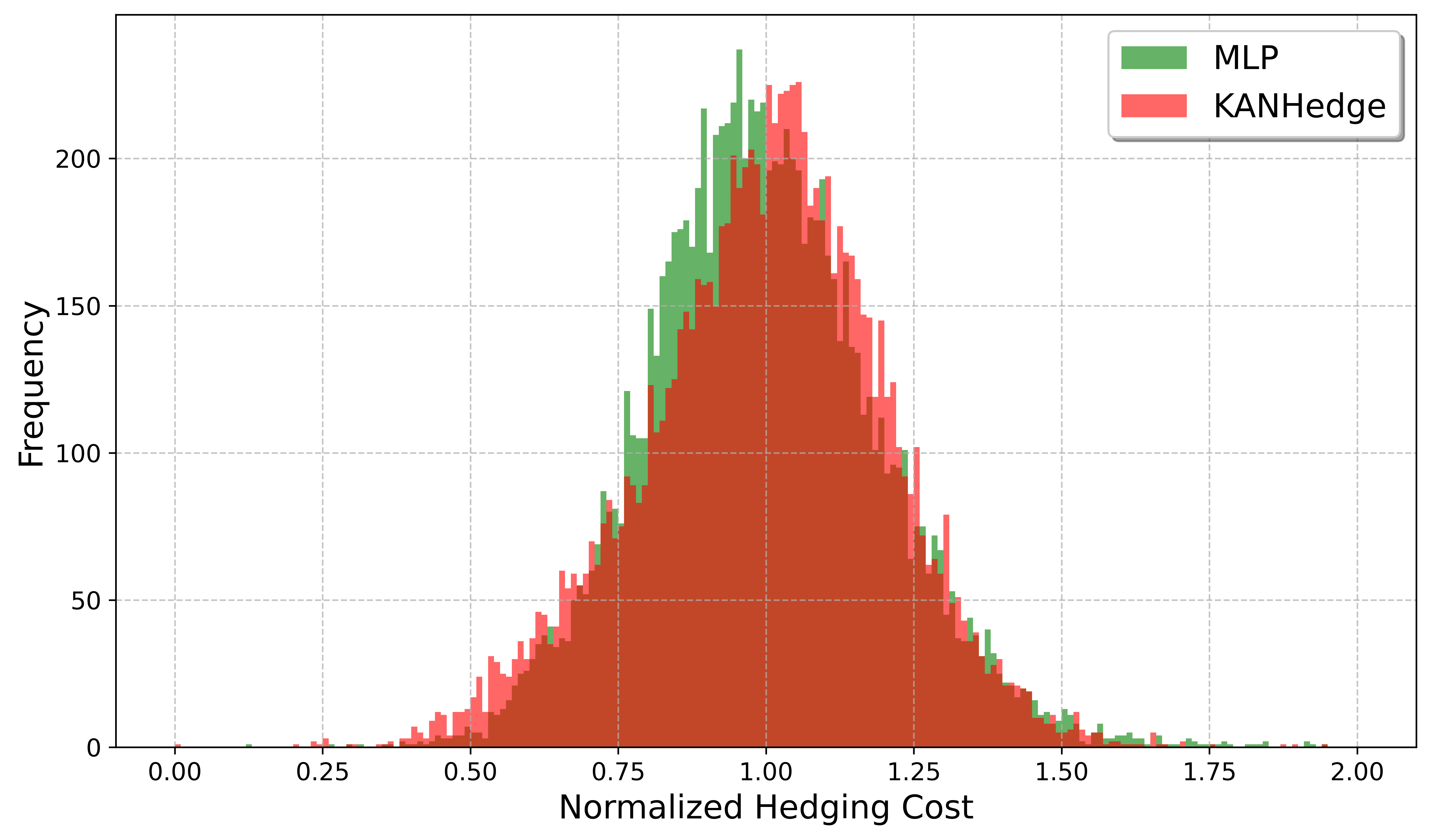
При параметрах [latex]\sigma_1 = 0.3[/latex], [latex]\rho = 0.3[/latex] и [latex]K = 35[/latex], стратегия KANHedge (красный) демонстрирует более низкие затраты на хеджирование американской корзинной опции по сравнению с MLP (зеленый). — При параметрах $\sigma_1 = 0.3$ , $\rho = 0.3$ и $K = 35$ , стратегия KANHedge (красный) демонстрирует более низкие затраты на хеджирование американской корзинной опции по сравнению с MLP (зеленый).

Влияние и перспективы повышения эффективности хеджирования

Точное ценообразование опционов и эффективное хеджирование играют первостепенную роль в минимизации затрат на хеджирование и управлении финансовыми рисками. Неспособность адекватно оценить стоимость опциона приводит к неоптимальным стратегиям хеджирования, увеличивая подверженность портфеля неблагоприятным движениям рынка и, как следствие, увеличивая общие издержки. Эффективное хеджирование, напротив, позволяет снизить волатильность портфеля и защитить от потенциальных убытков, обеспечивая стабильность и предсказуемость финансовых результатов. В конечном итоге, достижение точности в ценообразовании и эффективности в хеджировании является ключевым фактором для обеспечения финансовой устойчивости и максимизации прибыли в условиях неопределенности рынка.

Методы, такие как KANHedge, предоставляют специалистам возможность существенно снизить подверженность портфеля колебаниям рынка и повысить его эффективность. Исследования показывают, что применение KANHedge позволяет уменьшить затраты на хеджирование до 4% для европейских опционов и до 9% для американских опционов, в сравнении с традиционными методами, основанными на MLP. Оценка эффективности достигается посредством использования метрик управления рисками, в частности, $CVaR$ (Conditional Value at Risk), что позволяет более точно оценить потенциальные убытки в неблагоприятных сценариях и оптимизировать стратегии хеджирования для минимизации рисков и увеличения доходности портфеля.

Перспективные исследования направлены на адаптацию разработанных методов к более сложным производным финансовым инструментам, выходящим за рамки стандартных европейских и американских опционов. Особое внимание уделяется возможности применения полученных результатов в других областях финансового моделирования и управления рисками, таких как оценка экзотических опционов, моделирование кредитных деривативов и оптимизация инвестиционных портфелей. Ожидается, что расширение области применения позволит повысить эффективность управления рисками в различных финансовых сценариях и улучшить точность оценки стоимости сложных финансовых инструментов, способствуя более обоснованным инвестиционным решениям и снижению потенциальных убытков.

Исследование, представленное в данной работе, напоминает процесс вскрытия сложного механизма. Авторы, подобно инженерам-реверсерам, стремятся понять внутреннюю структуру финансовых инструментов, используя новаторский подход KANHedge. Эта система, основанная на сетях Колмогорова-Арнольда, позволяет более эффективно решать стохастические дифференциальные уравнения в частных производных (BSDE), что критически важно для точной оценки и хеджирования опционов высокой размерности. Как заметила Мария Кюри: «Ничто в жизни не дается даром, и нужно работать, чтобы получить желаемое». Этот принцип отражает суть представленной работы - кропотливое исследование и разработка новых методов для достижения более точных и эффективных финансовых решений. Успех KANHedge в решении задачи хеджирования сложных опционов подтверждает, что понимание базовых принципов и смелые эксперименты приводят к прорывным результатам.

Что дальше?

Представленный подход, использующий сети Колмогорова-Арнольда для решения обратных стохастических дифференциальных уравнений, демонстрирует, что даже в многомерных пространствах опционов можно найти обходные пути, пусть и требующие изрядной вычислительной мощи. Однако, стоит признать: сама природа хеджирования, как попытка удержать неуловимое, остается проблематичной. Точность, достигнутая KANHedge, - это не абсолютная истина, а лишь приближение, зависящее от архитектуры сети и качества данных. Попытка "взломать" рынок, пусть и с помощью элегантных математических конструкций, неизбежно наталкивается на его непредсказуемость.

Будущие исследования, вероятно, сосредоточатся на адаптивности. Способность сети не просто аппроксимировать решение, но и самообучаться на потоке рыночных данных, представляется ключевой. Интересным направлением является комбинация KANHedge с другими методами, например, с reinforcement learning, для создания самооптимизирующихся стратегий хеджирования. В конечном счете, задача не в создании идеального хеджа, а в понимании границ его применимости и умении адаптироваться к меняющимся условиям.

И, конечно, нельзя забывать о фундаментальном вопросе: является ли стремление к абсолютному хеджу вообще разумным? Возможно, сама суть рынка заключается в непредсказуемости, и попытка её "взломать" - это лишь иллюзия, позволяющая выиграть время, но не изменить саму природу вещей. Понимание этой диалектики - вот что действительно важно.

Оригинал статьи: https://arxiv.org/pdf/2601.11097.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-20 03:09