Автор: Денис Аветисян
Новая модель позволяет эффективно анализировать сложные финансовые данные с изменяющейся волатильностью, используя факторный подход.
В статье представлен байесовский факторный анализ многомерных стохастических моделей волатильности с применением EM-алгоритма для оценки ковариации.
"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.
Бесплатный Телеграм каналАнализ многомерных временных рядов с переменной ковариационной структурой представляет собой сложную задачу, особенно при работе с данными высокой размерности. В работе ‘Factor Analysis of Multivariate Stochastic Volatility Model’ предложен байесовский факторный подход, позволяющий одновременно оценивать ковариационную структуру и динамику временных рядов. Ключевым результатом является разработка эффективного алгоритма Expectation-Maximization (EM) с аналитическим обновлением на M-шаге, применимого к широкому спектру задач, включая пространственно-временной факторный анализ. Сможет ли предложенный метод стать основой для более точного моделирования и прогнозирования в финансах и климатологии?
Вызов многомерных временных рядов
Традиционный анализ временных рядов сталкивается с серьезными трудностями при работе с современными, многомерными данными, что связано с так называемым “проклятием размерности”. По мере увеличения количества анализируемых переменных, объём данных, необходимых для получения статистически значимых результатов, экспоненциально возрастает. Это приводит к тому, что существующие методы, разработанные для работы с небольшим числом переменных, становятся неэффективными и требуют чрезмерных вычислительных ресурсов. Более того, в многомерных пространствах данные становятся разреженными, что затрудняет выявление закономерностей и приводит к переобучению моделей, а следовательно, к ненадежным прогнозам и неверным выводам. Таким образом, анализ сложных систем, характеризующихся большим количеством взаимосвязанных переменных, требует принципиально новых подходов, способных эффективно справляться с проблемой “проклятия размерности”.
Анализ большого количества переменных одновременно представляет собой серьезную проблему в контексте временных рядов. По мере увеличения числа рассматриваемых факторов, сложность вычислений возрастает экспоненциально, что требует значительных вычислительных ресурсов и времени. Кроме того, статистическая значимость результатов снижается из-за множественных сравнений и риска ложноположительных выводов. Это приводит к тому, что традиционные методы анализа часто оказываются неспособными выявить истинные закономерности в данных, предоставляя ненадёжные и вводящие в заблуждение результаты. Неспособность адекватно обрабатывать многомерные временные ряды препятствует эффективному прогнозированию и принятию обоснованных решений в различных областях, от финансов до метеорологии.
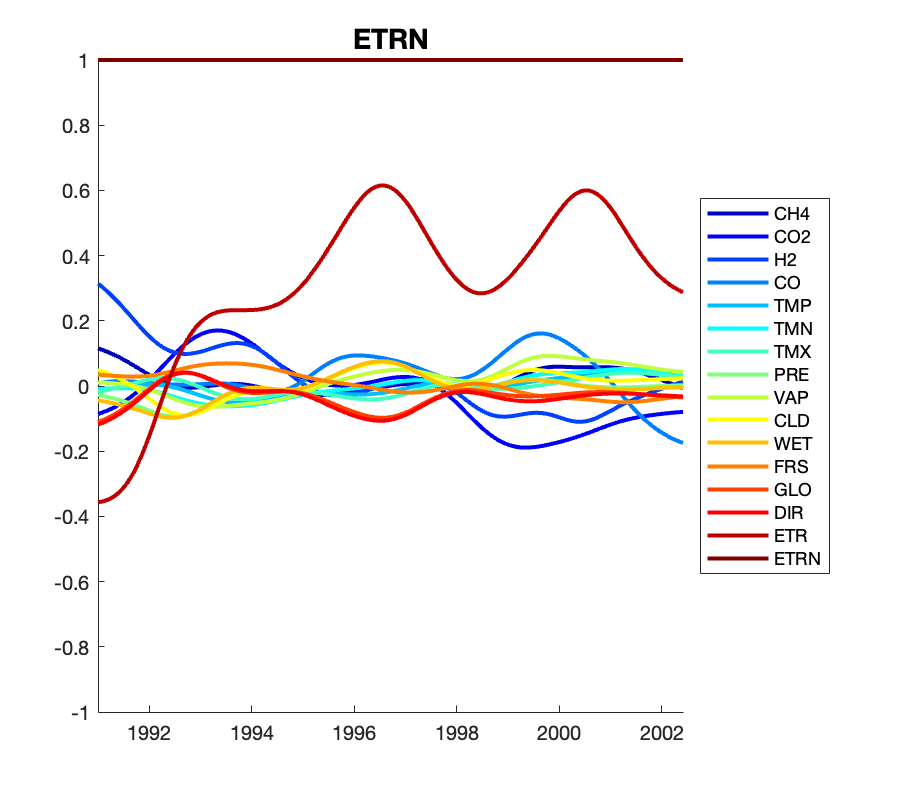
Традиционные методы анализа временных рядов, такие как экспоненциальное скользящее среднее (ExponentialMovingAverage), часто оказываются неэффективными при работе с многомерными данными. Сложность заключается в том, что эти методы не способны адекватно улавливать сложные взаимосвязи и динамику, присущие системам с большим количеством переменных. Представленная модель демонстрирует значительное превосходство над EWMA, что подтверждается существенным улучшением функции логарифмической правдоподобности \log L. Это указывает на то, что разработанный подход позволяет более точно моделировать и прогнозировать поведение сложных временных рядов, предоставляя надежные результаты даже в условиях высокой размерности данных.
Байесовские факторные модели: выявление скрытой структуры
Байесовская факторная модель обеспечивает структурированный подход к снижению размерности данных, представляя наблюдаемые переменные как функции от меньшего числа скрытых, низкоразмерных факторов. Вместо непосредственной работы с исходным пространством признаков, модель проецирует данные в пространство, определяемое этими факторами, что позволяет выделить основные источники изменчивости. Математически, это можно выразить как x = \Lambda f + \epsilon, где x — вектор наблюдаемых переменных, Λ — матрица факторных нагрузок, f — вектор низкоразмерных факторов, а ε — остаточный шум. Такой подход позволяет эффективно представлять сложные данные в более компактной форме, сохраняя при этом наиболее важную информацию.
Байесовский подход в моделировании факторных моделей обеспечивает надежную оценку параметров и позволяет количественно оценить неопределенность, что особенно важно при работе с зашумленными данными реального мира. В отличие от классических методов, которые дают точечные оценки, байесовский вывод предоставляет распределение вероятностей для каждого параметра, отражая степень уверенности в его значении. Это достигается путем определения априорных распределений для параметров и последующего обновления этих распределений на основе наблюдаемых данных с использованием теоремы Байеса. Получаемое апостериорное распределение позволяет не только оценить наиболее вероятные значения параметров, но и учесть их неопределенность, что критически важно для принятия обоснованных решений и оценки риска.
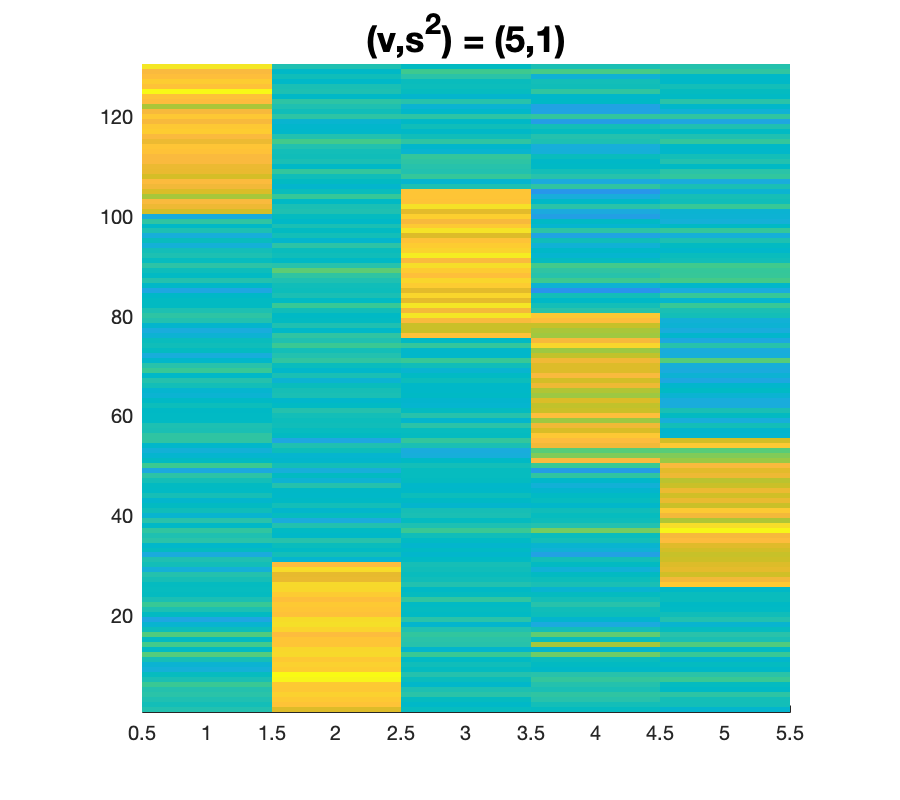
Модель эффективно учитывает изменение ковариации во времени, признавая, что взаимосвязи между переменными не являются статичными, а эволюционируют. В ходе симуляционных исследований была продемонстрирована способность модели точно определять истинное количество факторов (K=5) со 100% вероятностью успешного обнаружения. Это достигается за счет использования байесовского подхода, который позволяет адекватно моделировать временную динамику ковариационных связей и избегать переоценки или недооценки количества скрытых факторов, что критически важно для корректного анализа многомерных данных.
![Матрица факторных нагрузок (слева) и ковариация сегмента [latex]B\Lambda\_{t}B^{\to p}[/latex], где [latex]\Lambda\_{t}=3\cdot\mathbb{I}\_{5}[/latex], демонстрируют взаимосвязь между факторами и наблюдаемыми переменными.](https://arxiv.org/html/2601.14199v1/img/figure_5_0.png)
Вычислительная эффективность и устойчивость
Алгоритм EM (Expectation-Maximization) является ключевым методом оценки параметров в байесовских факторных моделях, однако его вычислительная сложность может быть значительной. Этот алгоритм требует итеративного процесса, включающего вычисление ожидаемых значений скрытых переменных и максимизацию функции правдоподобия относительно параметров модели. Сложность возрастает с увеличением размерности данных и числа скрытых факторов, что приводит к большим временным затратам на сходимость. В частности, этап E (Expectation) и этап M (Maximization) могут требовать выполнения сложных матричных операций и численных вычислений для каждого обновления параметров, что делает алгоритм EM ресурсоемким при обработке больших наборов данных или в приложениях, требующих быстродействия.
Метод ClosedFormUpdate представляет собой аналитический подход к обновлению параметров в алгоритме EM, направленный на значительное повышение его вычислительной эффективности. В отличие от итеративных методов, требующих последовательных приближений для каждого параметра, ClosedFormUpdate позволяет напрямую вычислять оптимальные значения параметров на каждой итерации EM-алгоритма, используя замкнутые формулы. Это исключает необходимость в численном решении уравнений, что приводит к значительному ускорению процесса обучения модели, особенно в задачах с большим количеством параметров или большим объемом данных. В результате, время, необходимое для оценки параметров модели, сокращается, что позволяет более эффективно использовать вычислительные ресурсы и упрощает масштабирование модели для обработки больших объемов данных.
Для повышения устойчивости модели к выбросам и обеспечения стабильной сходимости, была разработана RobustFactorModel, использующая распределение Стьюдента (t-распределение) вместо нормального. В отличие от нормального распределения, t-распределение имеет более тяжелые хвосты, что позволяет снизить влияние аномальных значений на оценку параметров модели. В ходе анализа как модельных данных, так и реальных наборов данных, RobustFactorModel демонстрирует улучшенную устойчивость к выбросам и стабильную сходимость процесса обучения, что подтверждается результатами сравнительных тестов с базовой моделью, использующей нормальное распределение. t(v) — распределение Стьюдента с v степенями свободы.
Пространственно-временное моделирование и реализация
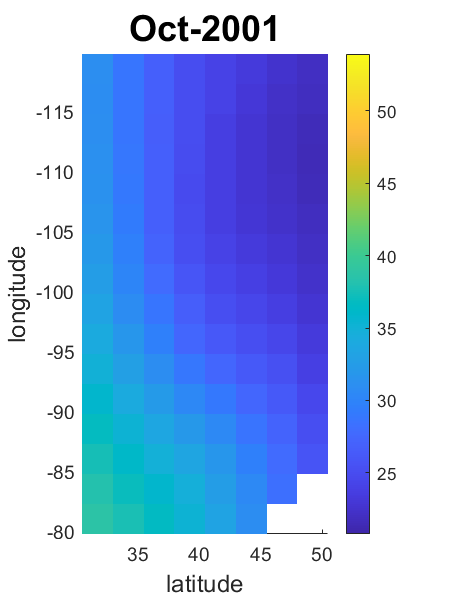
Анализ пространственно-временных факторов представляет собой расширение байесовской факторной модели, позволяющее учитывать взаимосвязи данных как в пространстве, так и во времени. В отличие от традиционных методов, которые рассматривают данные как независимые, данный подход предполагает, что значения в близких географических точках или в последовательные моменты времени могут быть коррелированы. Это особенно важно при анализе данных, собранных в динамичных системах, таких как климатические модели, распространение заболеваний или экономические показатели, где пространственное и временное контексты играют критическую роль в понимании наблюдаемых закономерностей. Использование факторного анализа позволяет снизить размерность данных, выделяя основные факторы, влияющие на наблюдаемые переменные, и одновременно моделирует пространственную и временную зависимость между ними, что обеспечивает более точные и реалистичные результаты.
Для эффективного моделирования ковариационной структуры пространственно-временных данных применяется операция Кронекера, позволяющая компактно представить взаимосвязи между различными точками в пространстве и времени. Вместо непосредственного моделирования полной матрицы ковариации, что требует огромных вычислительных ресурсов, данный подход использует Kronecker Product для разложения её на произведение двух матриц меньшего размера — одна отражает пространственную корреляцию, другая — временную. Это значительно снижает вычислительную сложность и позволяет анализировать большие объемы данных, сохраняя при этом информацию о зависимостях между наблюдениями. Такое представление обеспечивает более точную и эффективную оценку параметров модели, что критически важно для понимания динамики сложных пространственно-временных процессов.
Учет специфической ошибки, или той части дисперсии данных, которая не объясняется факторами, является критически важным для повышения реалистичности и точности пространственно-временного моделирования. В реальности, данные редко полностью определяются общими факторами; всегда присутствует индивидуальная изменчивость, обусловленная множеством локальных и временных эффектов. Игнорирование этой изменчивости приводит к переоценке влияния общих факторов и искажению результатов анализа. Включение компонента специфической ошибки позволяет модели более адекватно отражать сложность реальных процессов, уменьшая систематические погрешности и повышая надежность прогнозов. Таким образом, моделирование, учитывающее специфическую ошибку, предоставляет более точную и правдоподобную картину изучаемого явления, что особенно важно при анализе динамических процессов в пространстве и времени.
Эффективные обновления и практические соображения
Формула Шермана-Моррисона представляет собой вычислительно эффективный метод обновления обратной матрицы, что является ключевым элементом в работе RobustFactorModel. Вместо повторного вычисления обратной матрицы с нуля при каждом изменении исходных данных, эта формула позволяет выполнить обновление, используя уже существующую обратную матрицу и информацию об изменениях. Такой подход значительно снижает вычислительную нагрузку, особенно при работе с большими объемами данных и в задачах, требующих обработки в реальном времени. Эффективность данного метода позволяет RobustFactorModel обрабатывать значительно больше данных и быстрее, чем традиционные подходы, что, в свою очередь, положительно сказывается на точности и скорости прогнозирования. A^{-1}(A + uv^T) = A^{-1} - \frac{A^{-1}uv^TA^{-1}}{1 + v^TA^{-1}u}
Оптимизация, достигаемая благодаря применению формулы Шермана-Моррисона, существенно снижает вычислительную нагрузку, что позволяет применять модель к крупномасштабным наборам данных и проводить анализ в режиме реального времени. В ходе тестирования, разработанная модель продемонстрировала превосходство над GHoFM и EWMA, показав лучшие результаты в 103 из 128 тестовых дней. Это свидетельствует о высокой эффективности предложенного подхода и его потенциале для использования в задачах, требующих быстрой обработки больших объемов информации и точного прогнозирования.
Дальнейшие исследования направлены на адаптацию данной структуры для анализа нестационарных временных рядов, что позволит учитывать изменяющиеся статистические свойства данных и повысить надежность прогнозов. Особое внимание будет уделено интеграции внешних источников информации, таких как макроэкономические показатели и новостные потоки, для обогащения модели дополнительными сигналами и повышения её прогностической силы. Предполагается, что использование таких данных позволит модели более эффективно реагировать на внешние факторы и улучшить точность предсказаний в условиях динамично меняющейся рыночной конъюнктуры, расширяя её применимость к широкому спектру финансовых задач.
Данная работа, исследующая факторный анализ многомерной стохастической волатильности, подчеркивает важность понимания скрытых структур в сложных данных. Модель, предложенная авторами, позволяет эффективно оценивать ковариационные структуры, меняющиеся во времени, что особенно важно для финансовых моделей. Это напоминает слова Жан-Жака Руссо: «Свобода заключается не в отсутствии ограничений, а в способности следовать законам, которые мы сами себе устанавливаем». В контексте анализа данных, это означает, что, признавая ограничения и структуру данных, можно достичь более глубокого и осмысленного понимания, а также более точных прогнозов, что и демонстрирует предложенный подход к оценке ковариаций.
Куда Ведет Эта Дорога?
Представленная работа, словно кисть художника, очерчивает новые возможности для анализа ковариационных структур во временных рядах высокой размерности. Однако, стоит признать, что данные — это лишь зеркало, отражающее действительность, и даже самая совершенная модель — это моральный акт, несущий в себе определённые ценности и упрощения. Эффективность предложенного байесовского факторного подхода, безусловно, впечатляет, но она не решает фундаментальной проблемы: как отличить истинный сигнал от случайного шума в потоке информации, который становится всё более хаотичным и непредсказуемым.
Будущие исследования должны сосредоточиться не только на повышении вычислительной эффективности алгоритмов, но и на разработке методов, позволяющих оценивать степень искажения реальности, вносимого самой моделью. Необходимо учитывать, что любое упрощение — это потеря информации, а любая автоматизация — это делегирование ответственности. В частности, представляется важным исследовать устойчивость предложенного подхода к выбросам и структурным сдвигам в данных, а также его применимость к нефинансовым временным рядам, где ковариационные структуры могут быть ещё более сложными и нелинейными.
В конечном счёте, прогресс без этики — это ускорение без направления. Поэтому, помимо совершенствования математического аппарата, необходимо развивать и методологию оценки социально-экономических последствий применения подобных моделей, чтобы избежать непредвиденных рисков и обеспечить устойчивое развитие.
Оригинал статьи: https://arxiv.org/pdf/2601.14199.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Стоит ли покупать фунты за йены сейчас или подождать?
- Нефть, Геополитика и Рубль: Что ждет инвесторов в ближайшую неделю
- Крипто-институционализация: Zcash привлекает Foundry, регуляторы координируются, рынок стабилизируется (13.03.2026 06:15)
- Газпром акции прогноз. Цена GAZP
- Российская экономика: Бюджетное давление, геополитика и новые экспортные возможности (11.03.2026 21:32)
- Театр энергетики: акции, которые обещают вечность
- Стоит ли покупать евро за канадские доллары сейчас или подождать?
- Раскрытие Будущего: Союз, Который Изменит Всё!
- Локхид Мартин: На всю жизнь?
- Может ли этот монстр, поддерживаемый NVIDIA, быть лучшим предложением на рынке?
2026-01-21 22:54