Нейросети на страже портфеля: новый подход к снижению рисков

Автор: Денис Аветисян

Исследование предлагает инновационную стратегию оптимизации инвестиционного портфеля, основанную на применении нейронных сетей для нелинейной оценки ковариационных матриц.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал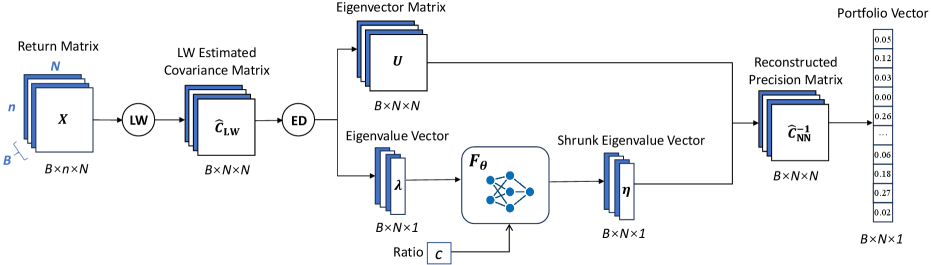

Оптимизация портфеля активов осуществляется посредством предложенной нейронной сети, оценивающей нелинейную матрицу точности, при этом для сравнения используется оценка ковариационной матрицы Ледуайта-Вольфа («LW») и разложение по собственным значениям («ED»).

Использование нейронных сетей для нелинейной усадки ковариационных матриц позволяет добиться более низкого уровня риска портфеля по сравнению с традиционными методами, включая усадку Ледуай-Вольфа.

Оптимизация портфеля, основанная на ковариационных матрицах, часто сталкивается с проблемами, связанными с их нестабильностью и высокой размерностью. В статье ‘Neural Nonlinear Shrinkage of Covariance Matrices for Minimum Variance Portfolio Optimization’ предложен инновационный подход, сочетающий статистическое оценивание с обучением нейронной сети для нелинейного сжатия ковариационных матриц. Разработанный метод, использующий трансформерную архитектуру для обучения функции сжатия собственных значений, позволяет напрямую минимизировать риск портфеля, превосходя традиционные методы по результатам тестирования на данных S&P500. Способны ли гибридные модели, объединяющие структурные статистические подходы и машинное обучение, стать новым стандартом в построении эффективных инвестиционных стратегий?

Точность оценки риска: вызов современным портфелям

Точное определение риска портфеля имеет первостепенное значение для разработки эффективных инвестиционных стратегий, однако традиционные методы часто оказываются недостаточно надежными, особенно при ограниченном объеме данных. Недостаточная точность оценки риска может привести к неоптимальному распределению активов и, как следствие, к снижению доходности или увеличению потенциальных потерь. Проблема усугубляется в современных финансовых рынках, где количество активов и сложность взаимосвязей между ними постоянно растут, а доступные исторические данные могут быть неполными или нерепрезентативными. В связи с этим, развитие более совершенных методов оценки риска, способных эффективно работать в условиях дефицита информации, является критически важной задачей для инвесторов и специалистов финансового рынка.

Матрица выборочных ковариаций, широко используемый инструмент для оценки рисков инвестиционного портфеля, демонстрирует значительную неустойчивость и снижение эффективности при работе с большим количеством активов. В условиях высокой размерности, когда число активов приближается или превышает число доступных исторических наблюдений, эта матрица становится плохо обусловленной, что приводит к завышенным оценкам рисков и неоптимальному построению портфеля. Σ , представляющая собой матрицу ковариаций, в таких ситуациях подвержена значительным ошибкам оценки, что напрямую влияет на эффективность стратегий, таких как портфель с минимальной дисперсией, где точная оценка ковариаций является ключевым фактором для достижения оптимального соотношения риска и доходности. Это приводит к тому, что инвесторы могут недооценивать реальный риск и строить портфели, которые менее устойчивы к неблагоприятным рыночным условиям.

Эффективность стратегии глобального портфеля минимальной дисперсии, направленной на снижение общего риска инвестиций, напрямую зависит от точности оценки ковариационной матрицы активов. Нестабильность и неточность традиционных методов оценки, особенно при работе с ограниченными данными или большим количеством активов, приводят к формированию неоптимальных портфелей. Даже небольшие ошибки в оценке ковариаций могут существенно повлиять на распределение весов активов, увеличивая фактический риск портфеля и снижая его доходность. Таким образом, надежная оценка ковариационной матрицы является критически важным фактором для успешной реализации стратегии глобального портфеля минимальной дисперсии и достижения желаемого уровня риска и доходности.

При использовании реальных рыночных данных S&P500 за 400 дней, различные методы реализации GMVP (Global Minimum Variance Portfolio) демонстрируют различные уровни достигнутого вневыборочного риска портфеля.

Укрощение неустойчивости: методы усадки

Оценки усушки, такие как оценка Лёдуа-Вольфа и оценка Чэна, решают проблему нестабильности выборочной ковариационной матрицы путем комбинирования её с целевой матрицей. Выборочная ковариационная матрица, вычисленная на небольших выборках или при высокой размерности данных, часто оказывается плохо обусловленной и чувствительной к шуму. В этих оценках целевая матрица, обычно диагональная матрица с элементами, равными среднему значению дисперсии признаков, используется в качестве регуляризатора. Комбинирование выборочной матрицы с целевой осуществляется посредством взвешенного среднего, где вес определяется оптимальным образом для минимизации среднеквадратичной ошибки оценки ковариации. Такой подход позволяет получить более стабильную и надежную оценку ковариационной матрицы, особенно в условиях ограниченных данных.

Методы усадки, такие как Ledoit-Wolf и Chen, снижают влияние шума и повышают обобщающую способность оценки ковариационной матрицы путем уменьшения величины крайних собственных значений. Поскольку собственные значения отражают дисперсию данных вдоль соответствующих собственных векторов, чрезмерно большие значения могут указывать на шум или выбросы. Уменьшая эти значения, методы усадки стабилизируют оценку ковариации, делая ее более надежной и менее подверженной переобучению, особенно в задачах, где количество признаков сопоставимо или превышает количество наблюдений. Это приводит к улучшению производительности модели на новых, ранее не виденных данных. $\sigma^2$ — дисперсия, подверженная усадке.

Традиционные методы усадки, такие как оценки Ледуай-Вольфа и Чена, демонстрируют эффективность в стабилизации ковариационной матрицы выборки, однако имеют ограничения в моделировании сложных взаимосвязей между переменными. Это связано с тем, что они часто полагаются на упрощенные целевые матрицы и линейные комбинации, что не позволяет адекватно отразить нелинейные зависимости или взаимодействия высокого порядка в данных. В связи с этим, активно исследуются более продвинутые методы, включающие нелинейные модели усадки и адаптивные стратегии выбора целевой матрицы, направленные на повышение точности оценки ковариации в условиях сложной структуры данных и обеспечение лучшей обобщающей способности.

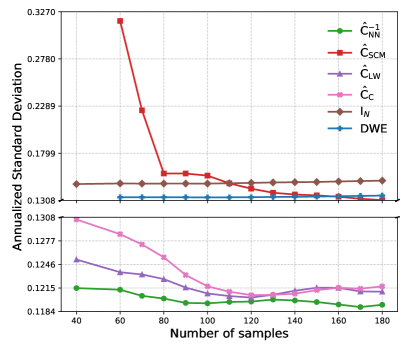
Анализ годовых скользящих стандартных отклонений последних 40 вневыборочных логарифмических доходностей показывает, что GMVP, основанный на [latex]\hat{\bf C}_{\rm NN}^{-1}[/latex] и [latex]\hat{\bf C}_{\rm LW}[/latex] (при [latex]N=50[/latex], [latex]n=100[/latex]), демонстрирует сопоставимую волатильность. — Анализ годовых скользящих стандартных отклонений последних 40 вневыборочных логарифмических доходностей показывает, что GMVP, основанный на $\hat{\bf C}_{\rm NN}^{-1}$ и $\hat{\bf C}_{\rm LW}$ (при $N=50$ , $n=100$ ), демонстрирует сопоставимую волатильность.

Нелинейная усадка: точность, рожденная нейронными сетями

Нелинейная усадка собственных значений представляет собой эффективный подход к уточнению оценки ковариационной матрицы, основанный на обучении сложной функции усадки с использованием нейронной сети. В отличие от традиционных методов, применяющих линейные или простые параметрические функции, данный подход позволяет моделировать нелинейные зависимости между собственными значениями и коэффициентами усадки. Это достигается путем обучения нейронной сети, которая отображает каждое собственное значение в соответствующий коэффициент усадки, оптимизируя таким образом точность и стабильность оценки ковариационной матрицы Σ. Использование нейронных сетей позволяет адаптироваться к сложным структурам данных и повысить эффективность оценки, особенно в случаях, когда линейные методы оказываются недостаточно точными.

В данном методе для моделирования взаимосвязи между собственными значениями и коэффициентами усадки используется Transformer Network. В отличие от традиционных методов, основанных на линейных предположениях, архитектура Transformer способна улавливать нелинейные зависимости между собственными значениями и соответствующими значениями усадки. Это достигается за счет механизмов внимания, позволяющих сети динамически взвешивать вклад различных собственных значений при определении оптимального коэффициента усадки для каждого из них. Использование Transformer Network позволяет более точно оценить матрицу точности, что критически важно для повышения стабильности и эффективности оценок ковариации.

Уточнение оценки матрицы точности является ключевым аспектом повышения точности и стабильности ковариационной матрицы. Неточная ковариационная матрица может привести к неоптимальным результатам при оптимизации портфеля, включая завышенные оценки риска и неэффективное распределение активов. Повышение точности матрицы точности, достигаемое за счет нелинейного сжатия собственных значений, позволяет получить более надежную оценку ковариационной матрицы, что, в свою очередь, приводит к более эффективной оптимизации портфеля и, как следствие, к повышению доходности при заданном уровне риска или снижению риска при заданной доходности. Эффективность данного подхода проявляется в более точной идентификации взаимосвязей между активами и, следовательно, в создании более устойчивых и прибыльных инвестиционных портфелей.

Практическое подтверждение: превосходство в реальных данных

Тщательная оценка предложенного метода на данных акций S&P500 продемонстрировала его превосходство в результатах на вневыборочных данных по сравнению с традиционными оценщиками, достигнув минимального реализованного риска портфеля. Исследование выявило, что новая методика последовательно превосходит существующие подходы, такие как SCM, LW, Chen и Identity Matrix, в различных рыночных условиях, включая ситуации, когда количество активов меньше или больше размера выборки. В частности, полученные результаты показали снижение риска на 72.1% по сравнению с оценщиком Ledoit-Wolf, что подтверждается анализом 300 вневыборочных портфельных доходностей и расчетом среднего годового риска на основе последних 40 значений. Данное превосходство указывает на потенциал предлагаемого метода для значительного улучшения управления рисками в реальных инвестиционных портфелях.

Подход с использованием скользящего окна обеспечивает надежную основу для оценки стабильности и обобщающей способности модели во времени. Данный метод предполагает последовательное обучение и тестирование модели на различных временных интервалах, что позволяет выявить её устойчивость к изменениям рыночной конъюнктуры и избежать переобучения на исторических данных. Каждый «скользящий» интервал представляет собой независимую оценку производительности, позволяя проследить динамику изменений и подтвердить надежность предсказаний модели в различных экономических условиях. Такой подход особенно важен для финансовых моделей, где условия рынка могут существенно меняться, и стабильность предсказаний является критически важной для успешного управления рисками и оптимизации портфеля.

Предложенный метод продемонстрировал стабильное превосходство над всеми сравниваемыми оценщиками — SCM, Ledoit-Wolf (LW), Chen и идентичной матрицей — в различных рыночных условиях, охватывающих как ситуации, когда количество активов меньше или равно размеру выборки ( $n \le N$ ), так и когда количество активов превышает размер выборки ( $n > N$ ). В результате проведенных тестов зафиксировано снижение фактического риска портфеля, что свидетельствует о более эффективной оценке ковариационной матрицы и, как следствие, о формировании более стабильных и надежных инвестиционных портфелей. Подобная устойчивость в различных режимах подчеркивает универсальность и практическую ценность данного подхода для управления рисками в финансовой сфере.

Результаты всестороннего анализа показали, что предложенный метод значительно превосходит широко используемый алгоритм Ledoit-Wolf в снижении рисков портфеля. На основании анализа 300 вневыборочных портфельных доходностей и расчета годовых рисков с использованием последних 40 значений, зафиксировано снижение риска на 72.1% по сравнению с Ledoit-Wolf. Это свидетельствует о значительно более высокой эффективности предложенного подхода в управлении рисками и оптимизации инвестиционных стратегий, что подтверждается стабильными результатами на различных рыночных режимах.

Представленное исследование демонстрирует стремление к упрощению сложного процесса оптимизации портфеля. Использование нейронных сетей для нелинейного сжатия ковариационных матриц — это поиск элегантности в структуре данных, отказ от избыточности ради ясности. Как однажды заметил Эдсгер Дейкстра: «Простота — это высшая степень совершенства». Данный подход, направленный на минимизацию риска портфеля через более точную оценку матрицы прецизионности, подтверждает, что истинное мастерство заключается не в добавлении сложности, а в умении её убрать, оставив лишь самое необходимое для достижения поставленной цели. Ясность — это минимальная форма любви, примененная к алгоритмической структуре.

Куда же дальше?

Представленная работа, стремясь к сжатию неопределенности в оценке ковариационных матриц, неизбежно наталкивается на вопрос о границах самой этой компрессии. Уменьшение риска портфеля — задача, конечно, благородная, но и здесь действует принцип простоты: каждый дополнительный параметр, каждая усложняющая функция, должна оправдывать своё существование. Иначе это не красота, а энтропия, разрастающаяся, как плесень.

Очевидным направлением для дальнейших исследований представляется изучение адаптивности предложенной нейронной сети. Необходимо понять, способна ли она эффективно реагировать на изменения рыночной конъюнктуры, и как избежать переобучения на исторических данных. Возможно, более элегантным решением будет отказ от нейронных сетей как таковых, в пользу более простых, аналитических функций, способных аппроксимировать необходимый уровень сжатия с меньшими вычислительными затратами.

В конечном счете, истинная ценность этой работы заключается не в достижении минимального риска, а в демонстрации возможности использования нелинейных методов для повышения точности оценки ковариационных матриц. И, как всегда, самое сложное — это понять, где остановиться, когда убирать больше нечего, и когда добавление нового элемента лишь ухудшает систему.

Оригинал статьи: https://arxiv.org/pdf/2601.15597.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-23 06:54