Обучение с подкреплением: Новый взгляд на градиенты

Автор: Денис Аветисян

Исследование предлагает улучшенный подход к обучению с подкреплением в стохастических средах за счет моделирования не только значений, но и их градиентов.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал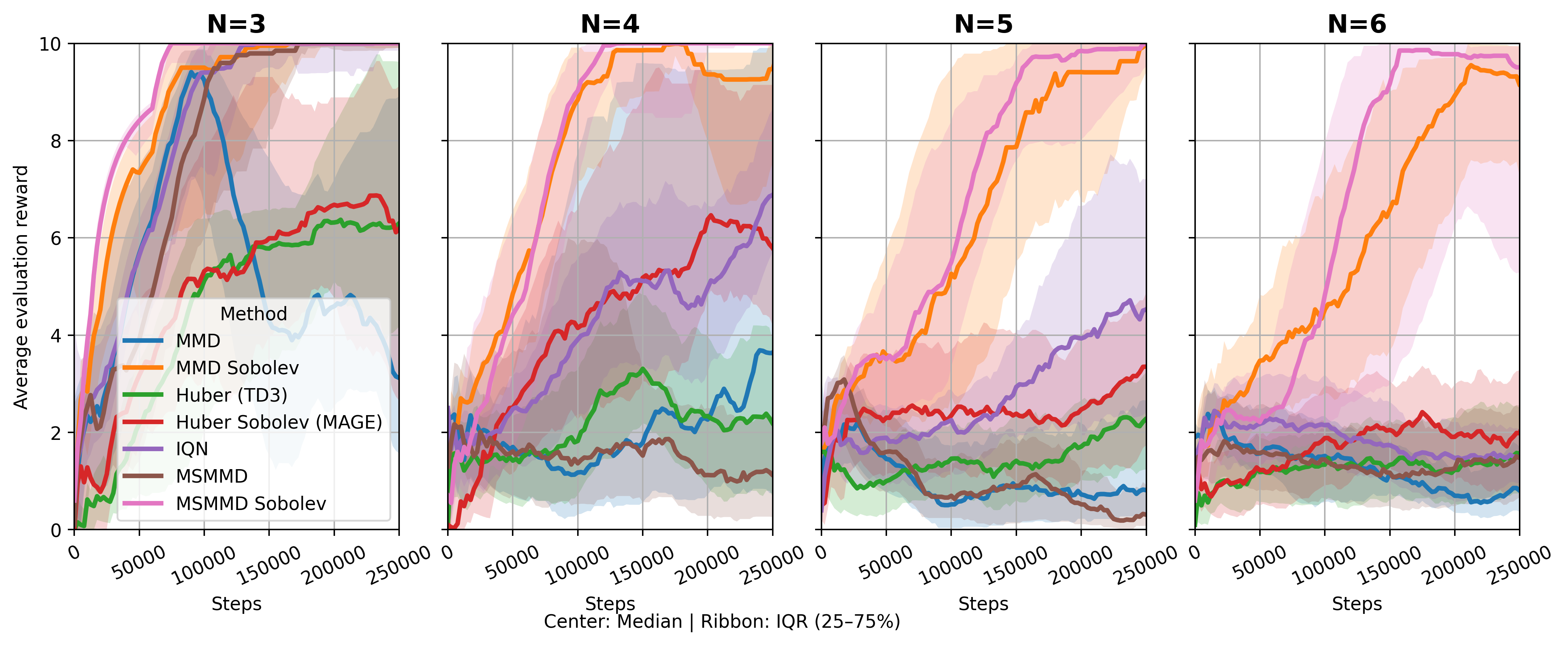

Исследование демонстрирует, что предложенные методы, основанные на Distributional Sobolev (в частности, MMD Sobolev и MSMMD Sobolev), превосходят детерминированные аналоги (MAGED’Oro и Jaskowski, 2020) и другие базовые подходы в среде двумерных точечных масс с множеством потенциальных бонусов, что подтверждается оценкой по кривым производительности (среднее по 5 случайным инициализациям с интерквартильным размахом 25%-75%) и свидетельствует о повышенной способности агента к достижению целей.

Предложен метод DSDPG, использующий распределённое обучение и пространства Соболева для повышения стабильности и эффективности в задачах с непрерывными пространствами действий.

Несмотря на успехи методов обучения с подкреплением, их эффективность в стохастических средах остается ограниченной из-за сложностей с оценкой градиентов. В данной работе, посвященной ‘Distributional value gradients for stochastic environments’, предложен подход, расширяющий обучение с подкреплением на основе распределений, для моделирования не только распределений значений состояний и действий, но и их градиентов. Используя концепцию пространства Соболева и условный вариационный автоэнкодер, авторы демонстрируют, что предложенный метод, Distributional Sobolev Training, обеспечивает устойчивость и улучшенную производительность в задачах с непрерывными пространствами состояний и действий. Каким образом моделирование градиентов в пространстве распределений может открыть новые горизонты для разработки более надежных и эффективных алгоритмов обучения с подкреплением?

За гранью данных: Экосистемы обучения с подкреплением

Традиционные алгоритмы обучения с подкреплением зачастую требуют колоссального объема данных для достижения приемлемой производительности, что существенно ограничивает их практическое применение. Данная зависимость от больших данных обусловлена сложностями точной оценки функций ценности и градиентов стратегии, особенно в сложных, реалистичных средах. Для эффективной работы в подобных условиях алгоритмам необходимо совершать огромное количество проб и ошибок, чтобы «научиться» оптимальному поведению. Это делает применение обучения с подкреплением в задачах, где сбор данных дорог или ограничен, крайне затруднительным. Например, в робототехнике, здравоохранении или финансовых моделях, где каждая ошибка может иметь серьезные последствия, или где доступ к данным строго регламентирован, потребность в алгоритмах, способных обучаться на ограниченном количестве примеров, становится критически важной.

Сложность точной оценки функций ценности и градиентов политики является фундаментальной проблемой, ограничивающей эффективность обучения с подкреплением. В сложных средах, характеризующихся высокой размерностью пространства состояний и действий, а также нелинейными зависимостями, стандартные алгоритмы сталкиваются с трудностями в обобщении полученного опыта. Недостаточность данных приводит к переоценке или недооценке определенных состояний или действий, что, в свою очередь, приводит к субоптимальной политике. $Q(s,a)$ — функция ценности, оценивающая ожидаемую награду за выполнение действия $a$ в состоянии $s$ — особенно подвержена ошибкам оценки при ограниченном количестве данных, что затрудняет выбор оптимальной стратегии поведения агента. Повышение точности этих оценок требует разработки более эффективных методов, способных извлекать максимальную пользу из ограниченного количества взаимодействий со средой.

Повышение эффективности использования данных имеет решающее значение для внедрения обучения с подкреплением в практические сценарии, где получение данных сопряжено с ограничениями или значительными затратами. В реальных приложениях, таких как робототехника или управление ресурсами, сбор большого объема данных может быть невозможен из-за физических ограничений, финансовых соображений или временных рамок. Поэтому разработка алгоритмов, способных обучаться на ограниченном количестве примеров, является ключевой задачей. Это позволит использовать обучение с подкреплением в более широком спектре приложений, включая те, где взаимодействие с окружающей средой дорогостоящее или рискованное. Успех в этой области откроет возможности для автоматизации сложных задач и оптимизации процессов в различных отраслях, несмотря на ограниченность доступных данных.

Обучение с учителем позволяет модели предсказывать распределение в выходном и градиентном пространствах, приближаясь к истинным пятимодальным данным после 25 000 шагов обучения, несмотря на использование детерминированной модели и [latex]L_2[/latex] потерь. — Обучение с учителем позволяет модели предсказывать распределение в выходном и градиентном пространствах, приближаясь к истинным пятимодальным данным после 25 000 шагов обучения, несмотря на использование детерминированной модели и $L_2$ потерь.

DSDPG: Обучение, ориентированное на градиенты

Алгоритм DSDPG использует метрику Maximum Mean Discrepancy (MMD) для моделирования как значений функций, так и их градиентов. MMD позволяет оценивать разницу между распределениями функций и их производных в пространстве признаков, что обеспечивает более точное приближение целевых распределений. Применение MMD к градиентам особенно важно для стабилизации обучения в задачах с высокой размерностью и сложными функциями вознаграждения. Это достигается путем минимизации расхождения между градиентами, предсказанными моделью, и градиентами, полученными из данных, что приводит к более устойчивому и надежному обучению по сравнению с методами, которые учитывают только значения функций.

В основе DSDPG лежит фреймворк Sobolev Temporal Difference (STD), который интегрирует информацию о градиентах в процесс обучения с подкреплением. В отличие от традиционных алгоритмов, использующих только значения функций, STD учитывает не только $Q(s,a)$ , но и $\nabla_{a}Q(s,a)$ — градиент функции ценности по действию. Это позволяет алгоритму более эффективно оценивать изменения в пространстве действий и, как следствие, ускоряет сходимость и улучшает стабильность обучения, особенно в задачах с высокой размерностью пространства состояний и действий. Использование градиентной информации позволяет алгоритму лучше адаптироваться к сложным ландшафтам вознаграждений и избегать локальных оптимумов.

Осознание градиентов позволяет DSDPG более эффективно исследовать сложные пространства состояний, что приводит к повышению эффективности использования данных. В процессе обучения алгоритм учитывает не только значения функции, но и направление ее изменения, что позволяет быстрее находить оптимальные решения и избегать локальных минимумов. Экспериментальные результаты, полученные в средах MuJoCo, демонстрируют, что DSDPG последовательно превосходит базовые алгоритмы, требуя меньше взаимодействий со средой для достижения аналогичного или лучшего уровня производительности. Это особенно важно в задачах с разреженными наградами и высокими размерностями пространства состояний.

Варианты DSDPG (MMD Sobolev и MSMMD Sobolev) демонстрируют сопоставимые или превосходящие результаты по сравнению с другими методами на шести задачах MuJoCo, особенно в условиях шума и повышенной сложности, что подтверждается оценкой по 10 случайным начальным значениям с указанием медианы и 95% доверительного интервала, рассчитанного с помощью Bootstrap.

Архитектура и оптимизация DSDPG

В DSDPG для управления и оценки действий используются две многослойные персептронные сети: сеть политики (Policy Network) и сеть критики (Critic Network). Обе сети построены с использованием архитектуры, включающей пропуски соединений (skip connections), что позволяет градиентам распространяться более эффективно и облегчает обучение более глубоких сетей. Сеть политики отвечает за выбор действий, основываясь на текущем состоянии среды, а сеть критики оценивает качество этих действий, предоставляя сигнал обратной связи для обучения сети политики. Использование пропусков соединений позволяет улучшить стабильность обучения и повысить эффективность сходимости алгоритма.

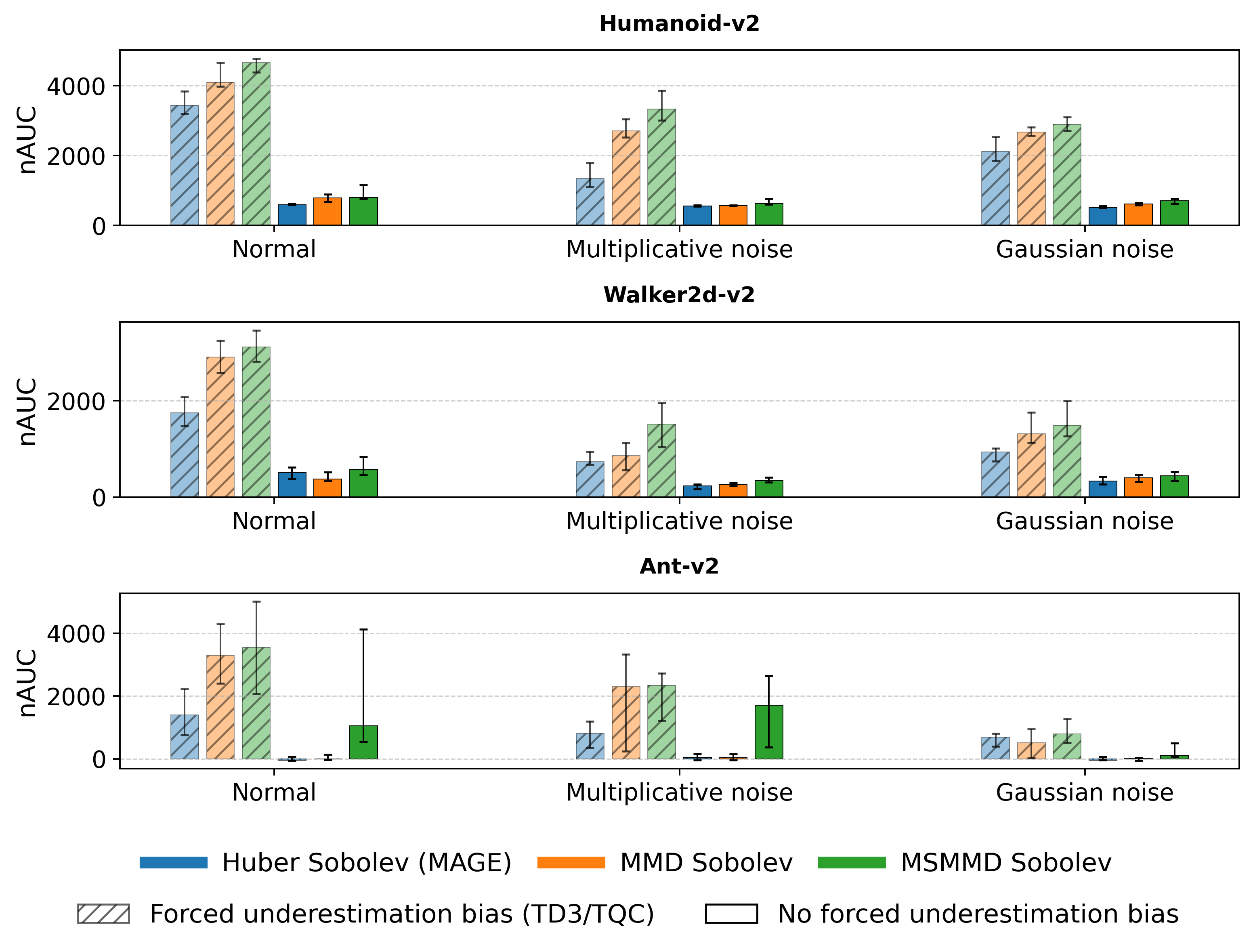
Процесс обучения DSDPG использует оптимизатор Rectified Adam, модификацию стандартного алгоритма Adam, предназначенную для улучшения сходимости и стабильности в задачах обучения с подкреплением. Для дальнейшей стабилизации обучения применяется метод TQC Truncation (Truncated Quantile Critic), который ограничивает разброс значений Q-функции, предотвращая переоценку и снижая вероятность выбора неоптимальных действий. TQC Truncation эффективно уменьшает смещение в оценках Q-функции, что приводит к более надежному и воспроизводимому обучению агента в сложных средах.

Для прогнозирования будущих состояний и обеспечения дифференцируемого обучения в DSDPG используется Мировая Модель, реализованная в виде условного вариационного автоэнкодера (CVAE). CVAE позволяет моделировать одношаговые переходы, предсказывая следующее состояние среды на основе текущего состояния и действия агента. В процессе обучения CVAE кодирует текущее состояние и действие в латентное пространство, а затем декодирует его обратно в предсказанное следующее состояние. Использование CVAE обеспечивает возможность вычисления градиентов через предсказания модели, что позволяет агенту обучаться на основе прогнозируемых, а не только реальных переходов, улучшая эффективность и стабильность обучения.

Алгоритм DSDPG, представленный в виде блок-схемы, использует критику [latex]Z_{\phi}[/latex] для отображения шума ξ и пары состояние-действие [latex](s, a)[/latex] в выборки Sobolev-возвратов, модель мира cVAE для генерации выборок следующего состояния и награды [latex](\hat{s}^{\prime},\hat{r})[/latex], а также MSMMD или MMD для сравнения предсказанных и бутстрап-распределений Sobolev-возвратов, что позволяет обновлять политику на основе среднего значения критики (направленные градиенты показаны пунктирными стрелками, вдохновлено Singhet al. (2022)); псевдокод для оценки смещенного MSMMD между предсказанными и бутстрап Sobolev-возвратами представлен справа. — Алгоритм DSDPG, представленный в виде блок-схемы, использует критику $Z_{\phi}$ для отображения шума ξ и пары состояние-действие $(s, a)$ в выборки Sobolev-возвратов, модель мира cVAE для генерации выборок следующего состояния и награды $(\hat{s}^{\prime},\hat{r})$ , а также MSMMD или MMD для сравнения предсказанных и бутстрап-распределений Sobolev-возвратов, что позволяет обновлять политику на основе среднего значения критики (направленные градиенты показаны пунктирными стрелками, вдохновлено Singhet al. (2022)); псевдокод для оценки смещенного MSMMD между предсказанными и бутстрап Sobolev-возвратами представлен справа.

Влияние DSDPG: Результаты в робототехнике

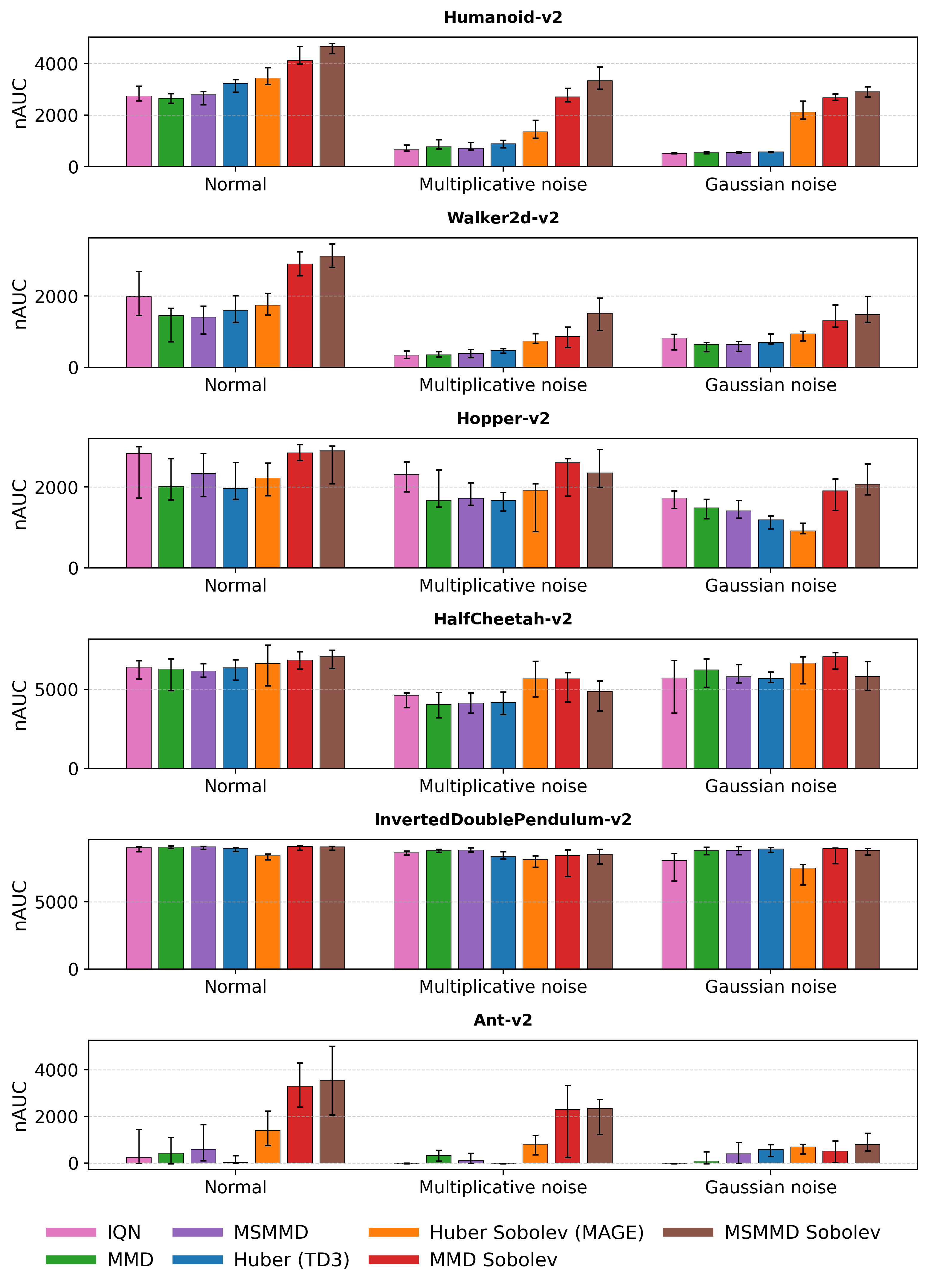
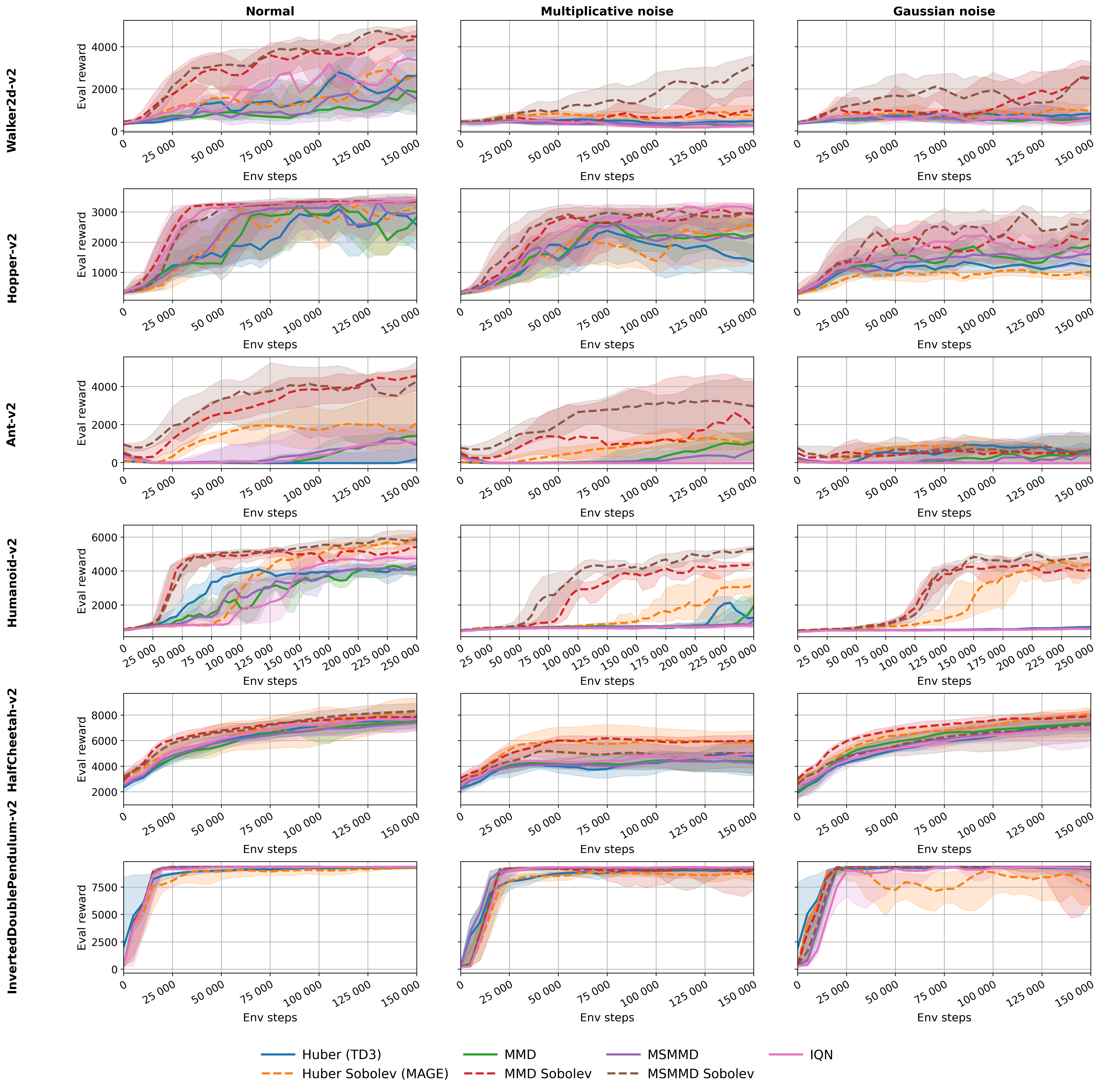
В ходе исследований, алгоритм DSDPG был протестирован в симуляторе физики MuJoCo, где он продемонстрировал превосходящие результаты по сравнению с базовыми алгоритмами, такими как TD3, IQN и MAGE. Эксперименты показали, что DSDPG стабильно превосходит конкурентов в различных задачах управления роботами, обеспечивая более эффективное обучение и улучшенные показатели производительности. Данное сравнение подтверждает потенциал DSDPG как перспективного подхода к разработке интеллектуальных систем управления, способного к адаптации и оптимизации в сложных динамических средах.

В ходе оценки алгоритма DSDPG в среде физического моделирования MuJoCo, ключевым показателем эффективности являлась суммарная награда (Cumulative Reward). Полученные результаты последовательно демонстрировали значительное улучшение этого показателя по сравнению с базовыми алгоритмами, такими как TD3, IQN и MAGE. Данное устойчивое превосходство указывает на существенный прирост в эффективности обучения, позволяя агентам быстрее осваивать оптимальные стратегии управления и достигать более высоких результатов в задачах роботизированного управления. Повышенная эффективность обучения, отраженная в суммарной награде, свидетельствует о потенциале DSDPG для создания более надежных и эффективных агентов обучения с подкреплением, применимых в реальных условиях.

Полученные результаты подчеркивают значительный потенциал DSDPG для ускорения разработки надежных и эффективных агентов обучения с подкреплением, применимых в реальных задачах. Эксперименты в среде MuJoCo продемонстрировали устойчивое превосходство DSDPG над базовыми алгоритмами, такими как TD3, IQN и MAGE, по ключевому показателю — накопленной награде. Это указывает на существенный прирост в эффективности обучения и открывает перспективы для более быстрого создания интеллектуальных систем управления, способных решать сложные задачи в различных областях, от робототехники до автоматизированного принятия решений. Устойчивое преимущество DSDPG над существующими методами позволяет предположить, что данный подход может стать важным инструментом для исследователей и разработчиков, стремящихся к созданию более совершенных и адаптивных систем искусственного интеллекта.

Оценка алгоритма DSDPG (MMD Sobolev) на шести задачах MuJoCo показала его эффективность, превосходящую или сопоставимую с алгоритмами, такими как Deterministic Sobolev/MAGED’Oro, Jaskowski (2020), TD3-Huber, IQN и стандартный MMD, при использовании медианного значения с межквартильным размахом 25%-75% и сглаживанием по скользящему окну размера 3.

Перспективы развития DSDPG

Дальнейшие исследования в области DSDPG могут быть направлены на расширение его применимости к более сложным и многомерным средам. Текущая эффективность алгоритма демонстрируется в относительно простых задачах, однако потенциал его масштабируемости остается предметом активных разработок. Особый интерес представляет возможность адаптации DSDPG к задачам, характеризующимся высокой степенью неопределенности и большим количеством параметров, таким как сложные робототехнические системы или управление сложными финансовыми моделями. Успешное решение этих задач потребует оптимизации алгоритма для эффективной обработки больших объемов данных и разработки новых стратегий исследования пространства состояний, что откроет новые возможности для применения DSDPG в различных областях науки и техники.

Интеграция DSDPG с передовыми методами, такими как иерархическое обучение с подкреплением и мета-обучение, открывает перспективные пути для повышения эффективности и адаптивности алгоритмов. Иерархическое обучение позволит разложить сложные задачи на более простые подзадачи, что упростит процесс обучения и повысит скорость сходимости. В свою очередь, мета-обучение позволит агенту быстро адаптироваться к новым, ранее не встречавшимся средам, используя полученный опыт от решения аналогичных задач. Комбинирование DSDPG с этими подходами может привести к созданию интеллектуальных систем, способных эффективно функционировать в динамичных и непредсказуемых условиях, демонстрируя значительный прогресс в области автономного обучения и управления. Особенно перспективным представляется использование мета-обучения для автоматической настройки гиперпараметров DSDPG, что позволит снизить вычислительные затраты и повысить обобщающую способность модели.

В ходе исследования значительную помощь оказало использование LLM-ассистента на различных этапах работы, включая отладку кода и форматирование математических уравнений, таких как $E=mc^2$ . Этот инструмент не просто облегчил рутинные задачи, но и способствовал повышению общей эффективности процесса разработки. Перспективы дальнейшей интеграции LLM-ассистентов в научные пайплайны представляются весьма многообещающими, позволяя автоматизировать трудоемкие операции, ускорить проверку гипотез и, в конечном итоге, стимулировать инновации в области искусственного интеллекта и машинного обучения. Возможность автоматического выявления и исправления ошибок в коде, а также аккуратного представления сложных формул, значительно снижает когнитивную нагрузку на исследователей и позволяет им сосредоточиться на более творческих аспектах работы.

Сравнение MAGE (D’Oro и Jaskowski, 2020) и DSDPG показывает, что исключение двойной оценки из MAGE и приема TQC из DSDPG позволяет избежать смещения и повысить точность оценки.

Исследование, представленное в статье, демонстрирует, что стремление к стабильности в системах обучения с подкреплением часто оказывается иллюзорным. Авторы предлагают подход, основанный на моделировании не только значений функций, но и их градиентов, используя пространства Соболева. Это позволяет системе адаптироваться к неопределенности и шуму, характерным для стохастических сред. Как однажды заметил Бертран Рассел: «Чем больше у нас информации, тем больше способов ее неверно истолковать». Иными словами, попытки жестко зафиксировать систему могут привести к непредсказуемым последствиям, тогда как гибкость и способность к адаптации — ключ к устойчивости. В данном случае, моделирование градиентов позволяет системе «чувствовать» направление изменений и корректировать свою стратегию, избегая застревания в локальных оптимумах.

Что дальше?

Представленная работа, стремясь обуздать стохастичность сред посредством моделирования градиентов, не столько решает проблему, сколько смещает фокус. Каждая зависимость, введённая для стабилизации обучения, — это обещание, данное прошлому, гарантия, что определённый класс сбоев не повторится. Однако системы живут циклами, и рано или поздно даже самые тщательно спроектированные механизмы самокоррекции начнут требовать внимания. Вопрос не в контроле — контроль есть иллюзия, требующая SLA — а в предвидении этих циклов, в построении систем, способных изящно пережить собственные ошибки.

Вместо того чтобы стремиться к идеальной модели мира, возможно, стоит сосредоточиться на создании систем, способных адаптироваться к неточностям этой модели. Пространства Соболева и расхождения максимального среднего — инструменты, но не цели. Истинная ценность заключается в понимании, что каждая архитектурная деталь — это пророчество о будущем сбое, и в проектировании систем, способных не просто выдерживать эти сбои, но и учиться на них.

Будущие исследования, вероятно, будут направлены на разработку методов, позволяющих динамически адаптировать сложность модели в зависимости от характеристик среды. Всё, что построено, когда-нибудь начнёт само себя чинить, но скорость и эффективность этого самовосстановления — ключевой фактор, определяющий жизнеспособность любой системы.

Оригинал статьи: https://arxiv.org/pdf/2601.20071.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-30 00:37