Адаптивные сетки: новый подход к балансу точности и эффективности

Автор: Денис Аветисян

В статье представлена унифицированная вариационная функциональность, позволяющая оптимизировать адаптивные сетки для достижения равномерного распределения и точной ориентации элементов.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

На примере 5.1 демонстрируется эволюция функционального значения сетки и минимального объема элемента при использовании предлагаемой функциональности и функциональности Хуанга с 25600 элементами, что позволяет оценить динамику изменения этих параметров в процессе оптимизации.

Предложенный метод объединяет принципы эквидистрибуции и выравнивания с использованием вариационного подхода и обеспечивает улучшенные теоретические свойства и стабильность.

Существующие вариационные функционалы для адаптивных сеток часто страдают от высокой нелинейности и зависимости от эмпирических параметров. В данной работе, посвященной ‘A Unified Variational Functional for Equidistribution and Alignment in Moving Mesh Adaptation’, предложен новый вариационный функционал, обеспечивающий равномерное распределение узлов и выравнивание элементов посредством $\boldsymbol A$ -отката, где $\boldsymbol A=\boldsymbol J^{-1}\boldsymbol M^{-1}\boldsymbol J^{-T}$ . Комбинация следового и логарифма определителя позволяет сбалансированно контролировать размер и анизотропию сетки без использования эмпирических параметров, а доказанные свойства коэрцитивности, поливыпуклости и геометрической выпуклости открывают новые возможности для эффективных алгоритмов адаптации сеток. Позволит ли предложенный подход создать более надежные и точные численные модели для широкого круга задач, включая гидродинамику и задачи с развивающимися границами?

Адаптивная Сетка: Вызов Эквидистрибуции

В многочисленных научных и инженерных расчетах, моделирование непрерывных сред часто требует дискретизации, то есть разбиения на отдельные элементы. Однако, этот процесс неизбежно приводит к накоплению ошибок в областях, где решение изменяется наиболее интенсивно. Например, при моделировании гидродинамики вокруг объекта, турбулентные вихри и ударные волны создают локальные градиенты, требующие высокой детализации сетки. Если сетка фиксирована и недостаточно плотна в этих критических зонах, точность моделирования резко снижается, а ошибки могут приводить к неверным выводам. В противоположность этому, излишне плотная сетка по всему расчетному пространству является неэффективной с точки зрения вычислительных ресурсов, поскольку большая часть усилий тратится на области, где решение меняется незначительно. Таким образом, задача поддержания необходимого уровня точности при одновременном снижении вычислительных затрат является ключевой в современной вычислительной науке.

Традиционные методы дискретизации, использующие фиксированную сетку, часто сталкиваются с трудностями при точном моделировании локализованных особенностей в сложных системах. В таких случаях, для достижения приемлемой точности решения, требуется значительно увеличить разрешение сетки по всему расчетному пространству, даже в областях, где изменения параметров незначительны. Это приводит к экспоненциальному росту вычислительных затрат и объема необходимой памяти, делая моделирование высокодетализированных явлений практически невозможным. Представьте, например, моделирование турбулентного потока: для точного разрешения мелких вихрей необходимо использовать чрезвычайно плотную сетку, хотя большая часть расчетного домена может характеризоваться плавными изменениями. В результате, фиксированные сетки оказываются неэффективными и дорогостоящими при решении задач, требующих высокой точности в ограниченных областях пространства.

Адаптивное уточнение сетки (AMR) представляет собой эффективный подход к решению задач, где требуется высокая точность в определенных областях расчетной области, однако его реализация требует тщательной проработки. Суть метода заключается в динамическом изменении плотности сетки: в областях с высокой скоростью изменения решения, сетка уплотняется, обеспечивая более детальное моделирование, а в областях с небольшими изменениями — напротив, упрощается, что позволяет существенно снизить вычислительные затраты. Ключевым аспектом является поддержание оптимального баланса между точностью и эффективностью, что достигается за счет разработки алгоритмов, определяющих критерии уточнения и упрощения сетки, а также методов интерполяции данных между различными уровнями сетки. Некорректный выбор этих параметров может привести к появлению артефактов, неточной аппроксимации решения или чрезмерным вычислительным затратам, поэтому разработка надежных и эффективных алгоритмов AMR является важной задачей современной вычислительной науки.

Сравнение результатов моделирования падения и подъема жидкости, полученных с использованием h-адаптивной (зеленый) и перемещающихся сеток на основе гессиана (красный) и разложения по собственным значениям (синий), демонстрирует соответствие траекторий вершины жидкости во времени.

Построение Функционала: Эквидистрибуция и Выравнивание

Построение функционала для адаптивной сетки (AMR) требует принципа равнораспределения, который обеспечивает равномерное распределение точек сетки относительно меры, характеризующей изменение решения. Это означает, что плотность точек сетки должна быть пропорциональна скорости изменения решения, например, градиенту или гессиану. Неравномерное распределение может привести к низкой точности в областях с высокой вариативностью решения и избыточному разрешению в областях с низкой вариативностью, что негативно сказывается на эффективности вычислений. Реализация этого принципа обычно включает в себя определение целевой плотности точек сетки на основе анализа решения и последующую адаптацию сетки для достижения этой плотности. $\frac{\partial u}{\partial x}$ и $\frac{\partial^2 u}{\partial x^2}$ являются типичными мерами вариативности, используемыми для определения необходимой плотности точек.

Принцип равномерного распределения узлов сетки в процессе функционального построения АМР должен быть тесно связан с принципом выравнивания. Выравнивание подразумевает приведение формы и расположения элементов сетки в соответствие с геометрией решения и его характеристиками, такими как градиенты и кривизна. Это означает, что плотность сетки должна увеличиваться в областях с высокой изменчивостью решения, а элементы сетки должны быть ориентированы вдоль направлений основного изменения, обеспечивая адекватное разрешение особенностей решения и повышая точность численного моделирования. Отсутствие выравнивания приводит к неэффективному использованию вычислительных ресурсов и снижению точности результатов.

Формулировка A-Pullback предоставляет эффективный способ упрощения как функционала, так и процесса дискретизации. Вместо работы непосредственно с геометрией исходной области, она использует отображение $A$ для перенесения задачи на эталонную область, обычно куб или прямоугольник. Это позволяет использовать более простые и структурированные сетки для дискретизации, что значительно снижает вычислительную сложность и упрощает реализацию алгоритмов. Упрощение функционала достигается за счет преобразования интегральных выражений с использованием якобиана отображения $A$ , что приводит к более компактной и удобной для анализа форме. Использование эталонной области также облегчает адаптацию сетки, поскольку можно использовать стандартные алгоритмы адаптивной дискретизации на кубе или прямоугольнике.

Для обеспечения корректности и устойчивости функционала, используемого в задачах адаптивной дискретизации, критически важны такие свойства, как масштабонезависимость, поливыпуклость и коэрцитивность. Масштабонезависимость $\text{scale invariance}$ гарантирует, что решение не зависит от единиц измерения, что обеспечивает физическую осмысленность результатов. Поливыпуклость $\text{polyconvexity}$ является необходимым условием для существования сильных локальных минимумов функционала, предотвращая возникновение нежелательных осцилляций и обеспечивая устойчивость решения. Коэрцитивность $\text{coercivity}$ , в свою очередь, гарантирует ограниченность решения и существование единственного минимума, что необходимо для сходимости численных методов и получения надежных результатов.

Распределения сетки для решения уравнения Бюргерса, полученные с использованием разработанной функциональной комбинации и метрики на основе длины дуги, демонстрируют стабильность решения в моменты времени [latex]t = 0.5[/latex] с, [latex]1[/latex] с и [latex]1.5[/latex] с. — Распределения сетки для решения уравнения Бюргерса, полученные с использованием разработанной функциональной комбинации и метрики на основе длины дуги, демонстрируют стабильность решения в моменты времени $t = 0.5$ с, $1$ с и $1.5$ с.

Реализация Движения Сетки: Градиентный Поток и Численные Решатели

Движение сетки в методе адаптивной локальной детализации (AMR) определяется градиентным потоком дискретной энергетической функциональности. Эта функциональность является дискретизацией непрерывной функциональности, представляющей собой целевую функцию оптимизации, которую необходимо минимизировать для достижения желаемого распределения сетки. Градиентный поток обеспечивает направление движения узлов сетки таким образом, чтобы уменьшить значение дискретной функциональности, тем самым улучшая качество сетки и точность решения. $\nabla E_d(x)$ представляет собой градиент дискретной энергетической функциональности $E_d$ в точке $x$ , который определяет скорость движения узлов сетки.

Для реализации движения сетки, определяемого градиентным потоком, требуется применение эффективных итерационных решателей. В частности, решатель Ньютона-Крылова показал свою эффективность в данной задаче. Для обеспечения требуемой точности вычислений, в процессе итераций используется критерий останова с допуском $10^{-6}$ . Данный уровень точности необходим для стабильной и корректной работы алгоритма, особенно при решении сложных задач вычислительной гидродинамики и физики плазмы.

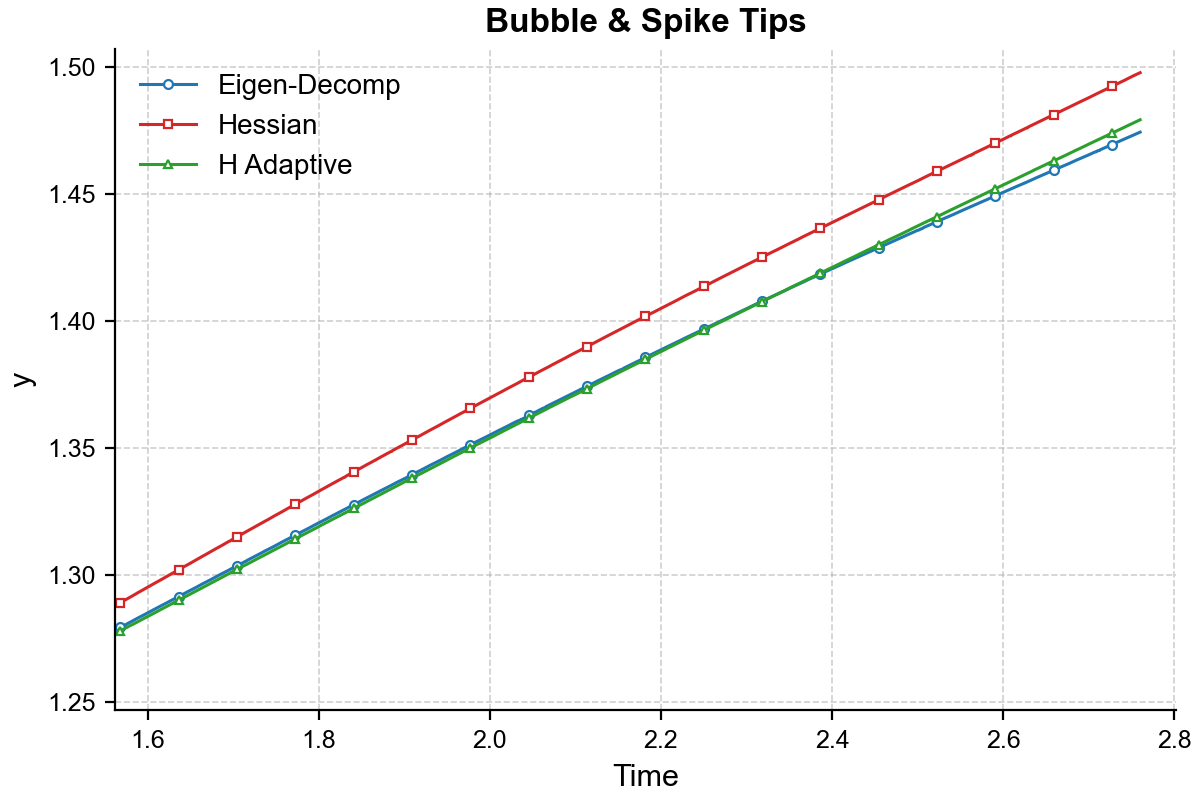
Применение разложения собственных значений (eigen-decomposition) позволяет значительно ускорить процесс решения системы линейных уравнений, возникающих при реализации градиентного потока для перемещения сетки. Предварительное вычисление собственных векторов и собственных значений матрицы системы позволяет перейти к диагональному представлению, упрощая и ускоряя итерационные методы, такие как метод Ньютона-Крилова. В частности, предварительное разложение позволяет эффективно вычислять обратную матрицу или решать системы уравнений с этой матрицей, снижая вычислительные затраты на каждой итерации и, следовательно, общее время решения. Это особенно полезно для больших и разреженных матриц, характерных для задач адаптивной сетки.

Эффективность метода адаптивной локальной сетки (AMR) была продемонстрирована при решении сложных задач, таких как уравнение Бергера и неустойчивость Рэлея-Тейлора. Достигнутая точность сопоставима с точностью, получаемой при использовании метода h-адаптивности, однако вычислительные затраты при использовании AMR составляют приблизительно в два раза больше. Это указывает на разумный компромисс между точностью и производительностью, делающий AMR жизнеспособным подходом для задач, требующих высокого разрешения в областях с большими градиентами, но при этом ограниченных вычислительных ресурсах.

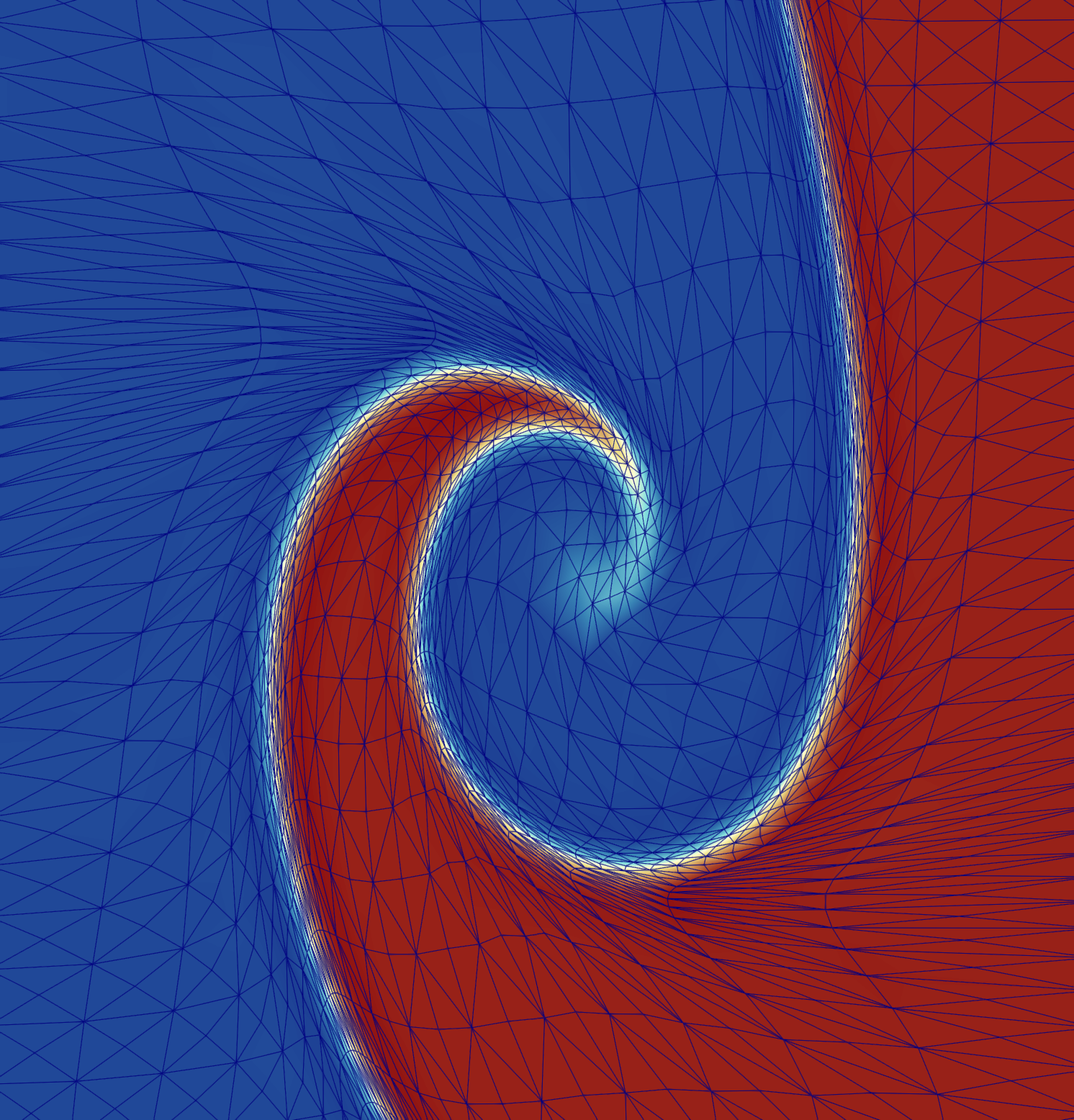
Распределение сетки при решении уравнения Бургера с использованием разработанной функциональной комбинации и метрики на основе гессиана демонстрирует стабильность и точность на временных отметках [latex]t = 0.5[/latex], [latex]1[/latex] и [latex]1.5[/latex] секунды. — Распределение сетки при решении уравнения Бургера с использованием разработанной функциональной комбинации и метрики на основе гессиана демонстрирует стабильность и точность на временных отметках $t = 0.5$ , $1$ и $1.5$ секунды.

Усиление Адаптивности: Метрики и Контроль Общего Объема

Выбор тензора метрики играет фундаментальную роль в определении локального масштабирования и ориентации элементов сетки. От этого выбора напрямую зависит точность и эффективность численного моделирования. Два основных подхода — использование метрик, основанных на длине дуги, и метрик, основанных на гессиане. Метрики, подобные длине дуги, стремятся сохранить форму элементов сетки, обеспечивая равномерное распределение разрешения вдоль кривых и поверхностей. В свою очередь, гессиан-основанные метрики учитывают кривизну исследуемой области, позволяя более точно адаптировать сетку к сложным геометрическим особенностям и концентрировать элементы в областях с высокой кривизной. Правильный выбор метрики позволяет эффективно управлять плотностью сетки, минимизируя вычислительные затраты и повышая точность результатов моделирования, особенно в задачах, связанных с анализом деформаций и течений.

Контроль общего объема метрики является ключевым аспектом поддержания стабильного размера сетки в процессе адаптивной детализации. В ходе численного моделирования, при увеличении разрешения в областях с высокой кривизной или сложными особенностями, важно предотвратить чрезмерное уменьшение элементов сетки по всей области. Регулируя общий объем метрики, алгоритм стремится к сохранению средней плотности элементов, эффективно распределяя ресурсы детализации именно в тех областях, где это необходимо для повышения точности решения. Данный подход позволяет избежать нежелательного увеличения вычислительных затрат, связанных с чрезмерной детализацией в областях, не требующих столь высокого разрешения, и гарантирует, что размер сетки остается управляемым и согласованным на протяжении всего процесса моделирования. Таким образом, поддержание постоянного общего объема метрики обеспечивает оптимальный баланс между точностью и эффективностью численного решения.

Для точного моделирования сложных геометрий и физических явлений необходимо установление соответствия между физической областью, представляющей реальный объект, и вычислительной областью, используемой для численного решения. Это достигается посредством координатного преобразования, которое отображает точки из физической области в вычислительную. Ключевую роль в этом процессе играет матрица Якоби, представляющая собой производные координатного преобразования и определяющая локальную деформацию и искажение элементов сетки. Аккуратное вычисление и отслеживание матрицы Якоби позволяет корректно учитывать изменения масштаба и ориентации, гарантируя, что решения, полученные в вычислительной области, адекватно отражают поведение в физической области, что особенно важно при адаптивном изменении размера сетки для повышения точности и эффективности моделирования.

Точное отслеживание функции плотности метрики является ключевым для поддержания необходимого уровня адаптивности расчетной сетки. В процессе моделирования, для обеспечения стабильности и точности, используются специфические параметры: $\gamma = 1.25$ и $\tau = 0.004$ . Значение γ влияет на скорость изменения плотности метрики, предотвращая чрезмерные локальные искажения, а параметр τ контролирует чувствительность к изменениям кривизны поверхности. Использование фиксированного размера временного шага, равного 0.05, гарантирует, что адаптация сетки происходит плавно и согласованно на протяжении всего расчета, что особенно важно для сложных геометрических форм и динамических процессов.

Локальные увеличения структуры сворачивания показывают, что метрика на основе гессиана и метрика на основе разложения по собственным значениям позволяют визуализировать схожие особенности её формирования.

Представленная работа демонстрирует стремление к созданию систем, способных к долгосрочной адаптации и сохранению целостности. Как отмечал Исаак Ньютон: «Если я вижу дальше других, то это потому, что стою на плечах гигантов». Аналогично, предложенный вариационный функционал опирается на существующие методы адаптации движущихся сеток, но предлагает более изящное и эффективное решение для обеспечения как равномерного распределения элементов, так и их согласованности. Это позволяет создавать сетки, которые не просто адаптируются к текущим условиям, но и сохраняют свою структуру и предсказуемость на протяжении длительного времени, минимизируя накопление ‘технического долга’ в процессе вычислений и обеспечивая устойчивость решения.

Что впереди?

Представленная работа, подобно любому тщательно выстроенному каркасу, обнажает не только достигнутое, но и горизонты нерешенных вопросов. Уравновешивание эквидистрибуции и выравнивания в адаптивных сетях — это не статичная цель, а скорее динамический процесс, требующий постоянной калибровки. Логирование изменений метрического тензора, эта своеобразная хроника жизни системы, позволяет отслеживать деформации, но не предсказывает их. Следующим шагом представляется исследование возможностей интеграции предсказательных моделей, способных учитывать влияние внешних факторов и нелинейностей, в процесс адаптации сетки.

Вариационный функционал, предложенный в данной работе, демонстрирует улучшенные теоретические свойства и сниженную нелинейность. Однако, развертывание этого функционала в реальных задачах — лишь мгновение на оси времени. Остается открытым вопрос о его масштабируемости на задачи высокой размерности и о возможности адаптации к сложным геометриям. Необходимо исследовать альтернативные подходы к геометрической дискретизации, которые могли бы обеспечить большую гибкость и точность.

Все системы стареют — вопрос лишь в том, делают ли они это достойно. Адаптивные сетки, подобно живым организмам, нуждаются в постоянном обновлении и совершенствовании. Истинный прогресс заключается не в создании идеальной сетки, а в разработке методов, позволяющих ей эволюционировать и приспосабливаться к изменяющимся условиям. Именно в этом направлении представляется наиболее перспективным путь дальнейших исследований.

Оригинал статьи: https://arxiv.org/pdf/2601.20235.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-30 05:38