Траектория Победы: Обучение Автономных Гоночных Автомобилей

от

Автор: Денис Аветисян

Новый подход к оптимизации траекторий для автономных гоночных автомобилей позволяет значительно сократить время круга благодаря учету специфики трассы и динамики транспортного средства.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал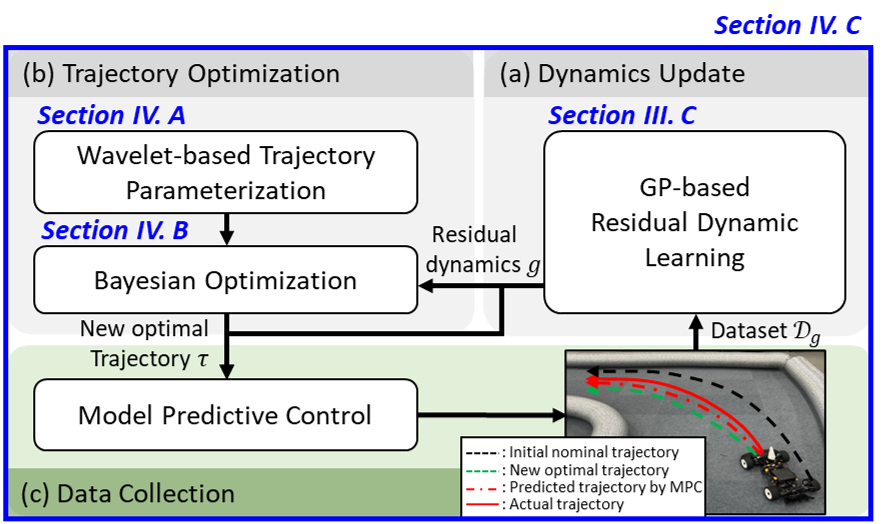
Итеративное обучение, ориентированное на траектории, формирует архитектуру, в которой система не конструируется, а эволюционирует посредством последовательных циклов, предсказывая будущие точки отказа в каждом архитектурном решении.
Итеративное обучение, ориентированное на траектории, формирует архитектуру, в которой система не конструируется, а эволюционирует посредством последовательных циклов, предсказывая будущие точки отказа в каждом архитектурном решении.

Предложена track-centric итеративная схема обучения для глобальной оптимизации траекторий, использующая параметризацию вейвлетами, байесовскую оптимизацию и учет остаточных динамических свойств автомобиля.

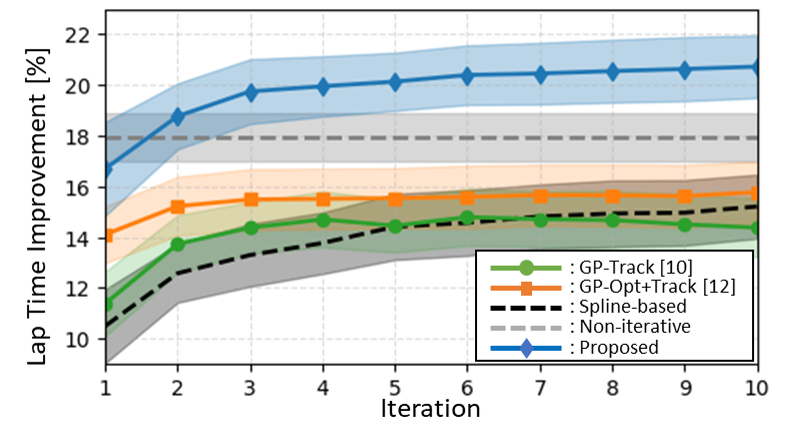
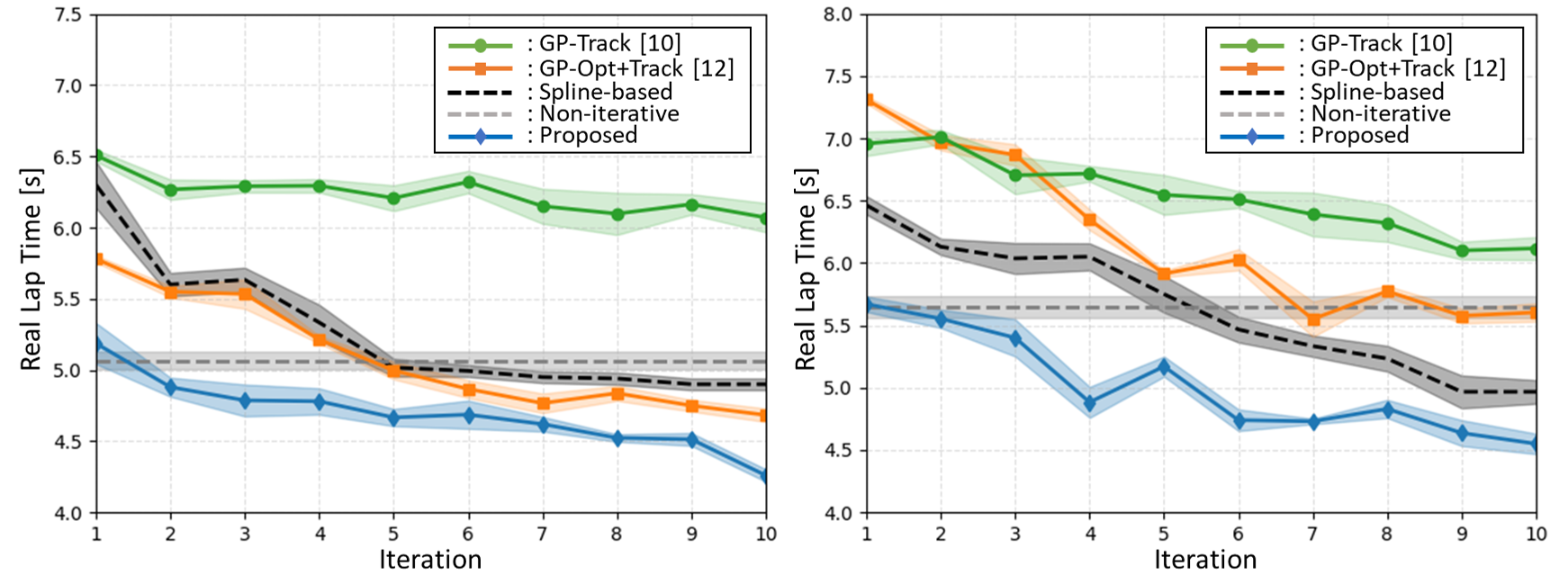
Оптимизация траектории гоночного автомобиля на протяжении всего круга является вычислительно сложной задачей, а учет неопределенности динамики автомобиля в реальном времени затрудняет достижение глобальной оптимальности. В данной работе, посвященной ‘Track-centric Iterative Learning for Global Trajectory Optimization in Autonomous Racing’, предлагается новый подход, основанный на итеративном обучении и оптимизации траектории с учетом специфических для трассы характеристик динамики автомобиля. Предложенная методика, использующая параметризацию траектории на основе вейвлет-преобразования и байесовскую оптимизацию, позволяет улучшить время прохождения круга до 20.7% по сравнению с базовым уровнем. Каковы перспективы масштабирования данного подхода для решения задач автономной навигации в более сложных и непредсказуемых условиях?

Симфония Скорости: Постановка Задачи Автономных Гонок

Автономные гонки представляют собой уникальную задачу, требующую достижения оптимальной производительности в динамичных и высокоскоростных условиях. В отличие от традиционной робототехники, где приоритетом является надежность и безопасность, здесь ключевым фактором является скорость и точность маневрирования на пределе возможностей транспортного средства. Эта среда характеризуется постоянными изменениями, непредсказуемым поведением соперников и необходимостью мгновенного принятия решений, что требует от систем автономного управления способности адаптироваться к непрерывно меняющимся условиям и эффективно использовать все доступные ресурсы для максимизации скорости и сохранения траектории. Сочетание высокой скорости и динамичности предъявляет повышенные требования к сенсорным системам, алгоритмам планирования траектории и системам управления, делая автономные гонки сложной, но перспективной областью исследований в области искусственного интеллекта и робототехники.

Для достижения успеха в автономных гонках требуется не просто управление транспортным средством, а предельно точный контроль над каждым аспектом его движения, позволяющий максимально эффективно использовать возможности автомобиля на сложных трассах. Это подразумевает способность беспрепятственно проходить повороты на максимальной скорости, мгновенно реагировать на изменения дорожного покрытия и оптимизировать траекторию движения в реальном времени. По сути, речь идет о создании системы, способной действовать на грани физических возможностей автомобиля, постоянно балансируя между скоростью и устойчивостью, и адаптироваться к непредсказуемым условиям гоночной трассы, чтобы обеспечить стабильно высокие результаты.

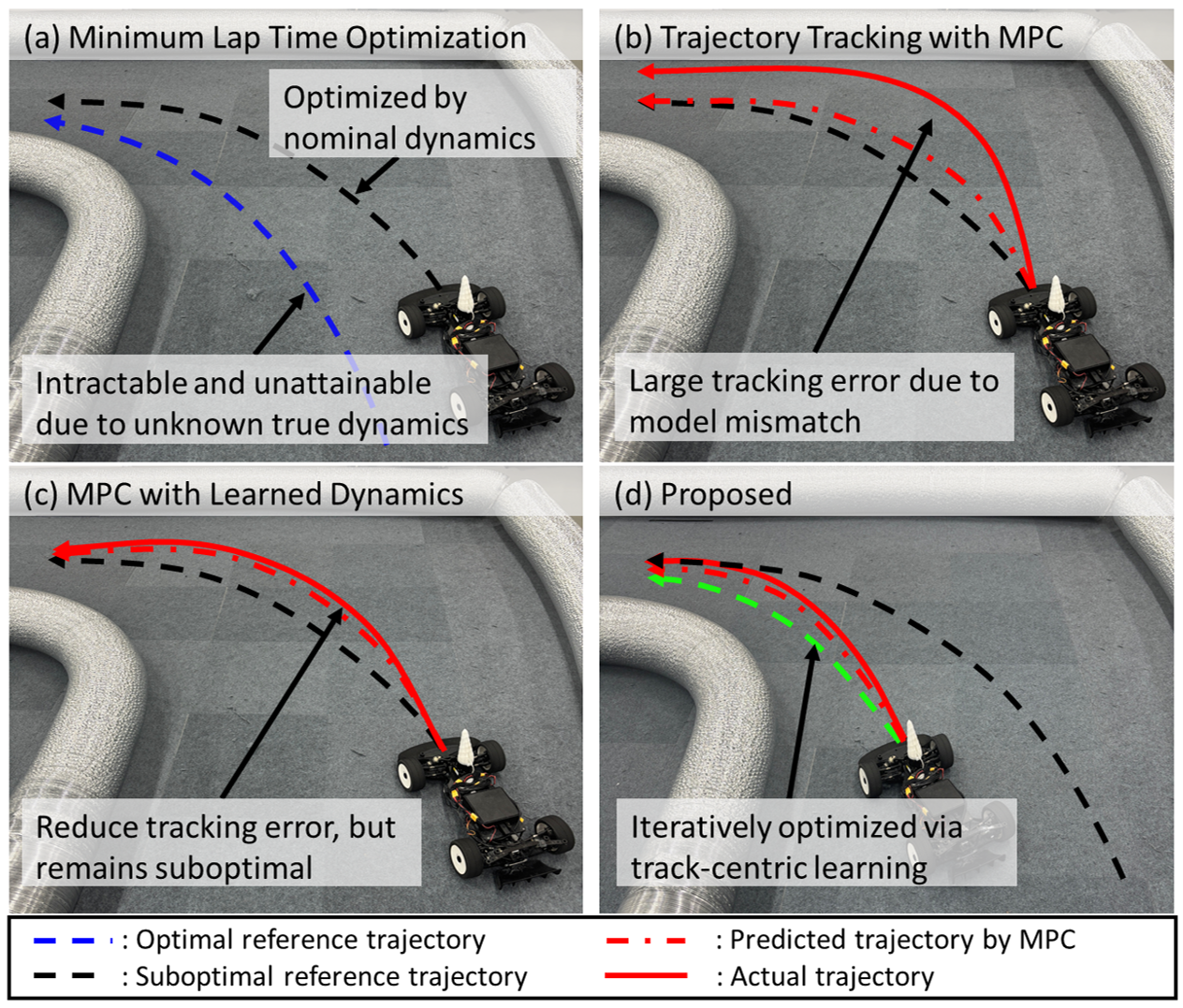
Традиционные методы планирования траектории движения часто сталкиваются с серьезными вычислительными трудностями, особенно в условиях динамичных гоночных трасс. Оптимизация траектории в реальном времени требует огромных ресурсов, а жесткие ограничения по времени реакции не позволяют использовать сложные алгоритмы. К тому же, стандартные подходы испытывают трудности при адаптации к непредвиденным изменениям на трассе — неровностям покрытия, меняющимся условиям сцепления или внезапным препятствиям. В результате, существующие системы часто демонстрируют недостаточную точность и стабильность, что препятствует достижению максимальной скорости и эффективности в гоночных соревнованиях. Поэтому, разработка новых, более эффективных методов планирования движения, способных оперативно реагировать на изменяющиеся условия и оптимизировать траекторию в реальном времени, является ключевой задачей в области автономных гонок.

Для достижения успеха в автономных гонках требуется разработка принципиально новых подходов к моделированию и прогнозированию поведения автомобиля. Традиционные алгоритмы зачастую не справляются с вычислительной сложностью, необходимой для оперативного планирования траектории и адаптации к постоянно меняющимся условиям на треке. В связи с этим, исследователи активно применяют методы машинного обучения, в частности, глубокие нейронные сети, для создания моделей, способных эффективно прогнозировать динамику автомобиля и оптимизировать управление в реальном времени. Эти модели учатся на больших объемах данных, полученных в ходе симуляций и реальных заездов, позволяя автомобилю предвидеть изменения в траектории, учитывать факторы, влияющие на сцепление с дорогой, и выбирать оптимальные параметры управления для достижения максимальной скорости и точности.

Предложенный подход итеративно оптимизирует траекторию, позволяя уменьшить ошибку отслеживания и улучшить время прохождения, в отличие от стандартной оптимизации и MPC, которые либо дают субоптимальные траектории, либо испытывают значительные отклонения из-за неточности модели.
Предложенный подход итеративно оптимизирует траекторию, позволяя уменьшить ошибку отслеживания и улучшить время прохождения, в отличие от стандартной оптимизации и MPC, которые либо дают субоптимальные траектории, либо испытывают значительные отклонения из-за неточности модели.

Моделирование Динамики: Эмпирический Фундамент

Для построения точных моделей поведения транспортных средств, применяются методы, основанные на анализе данных, что позволяет учитывать сложные взаимодействия между компонентами и остаточные динамические эффекты. Традиционные аналитические модели часто упрощают реальные процессы, в то время как data-driven подходы, используя большие объемы эмпирических данных, позволяют идентифицировать и моделировать нелинейности, гистерезис и другие явления, которые сложно предсказать теоретически. Это особенно важно при моделировании динамики автомобиля в условиях реального вождения, где учитываются такие факторы, как износ шин, изменение параметров подвески, влияние дорожного покрытия и аэродинамические эффекты. Использование методов машинного обучения, таких как регрессия, нейронные сети и гауссовские процессы, позволяет создать модели, способные точно предсказывать поведение автомобиля на основе данных, полученных от датчиков и телеметрии.

Упрощенная модель велосипеда, дополненная системой координат Френе, является эффективным инструментом для представления динамики транспортного средства. Данная модель оперирует двумя основными точками — центром масс передней оси и центром масс задней оси — и рассматривает автомобиль как систему, движущуюся в плоскости. Система координат Френе, основанная на тангенциальной и нормальной осях траектории движения, позволяет описывать положение и ориентацию автомобиля относительно трассы, упрощая расчет сил и моментов, действующих на него. \dot{x}, \dot{y} представляют собой скорости в координатах Френе, а φ — угол рыскания. Несмотря на свою простоту, модель позволяет достаточно точно описывать основные характеристики движения, такие как радиус поворота, скорость и угловая скорость, что делает ее полезной для разработки и тестирования систем управления транспортным средством.

Понимание остаточных динамических эффектов — разницы между математической моделью поведения автомобиля и реальным поведением — является ключевым фактором повышения точности предсказаний. Эта разница возникает из-за упрощений, сделанных при создании модели, а также из-за не учтенных факторов, таких как шероховатость дорожного покрытия, износ шин, и нелинейности в подвеске. Анализ остаточных динамических эффектов позволяет выявить систематические ошибки модели и внести корректировки, улучшающие ее адекватность. Количественная оценка этих остатков, например, через расчет e = y_{real} - y_{model}, где y_{real} — фактическое поведение, а y_{model} — предсказанное, позволяет определить области, требующие дальнейшего уточнения модели и повышения ее точности.

Использование данных позволяет создать трек-центричную суррогатную модель, специфичную для каждой гоночной трассы. Данная модель строится на основе данных, собранных непосредственно на конкретной трассе, включая телеметрию, данные датчиков и информацию о покрытии. Это позволяет учесть уникальные особенности каждого участка трассы — углы поворотов, перепады высот, характеристики асфальта — и создать более точную модель поведения автомобиля. В отличие от универсальных моделей, трек-центричная суррогатная модель оптимизирована для конкретной трассы, что значительно повышает точность прогнозирования и позволяет эффективно использовать ее для планирования траектории, оптимизации настроек автомобиля и разработки систем помощи водителю. Она представляет собой аппроксимацию сложной динамики автомобиля, полученную на основе эмпирических данных, и может использоваться для быстрого и точного предсказания поведения автомобиля в различных сценариях.

Предложенный метод, использующий итеративное обучение динамики на основе симуляции, позволяет значительно сократить время прохождения трассы - в среднем на 20.7% по сравнению с базовым уровнем и превосходит другие подходы благодаря непосредственной оптимизации реального времени прохождения, что подтверждается результатами, представленными на рисунках 5 и 6.
Предложенный метод, использующий итеративное обучение динамики на основе симуляции, позволяет значительно сократить время прохождения трассы — в среднем на 20.7% по сравнению с базовым уровнем и превосходит другие подходы благодаря непосредственной оптимизации реального времени прохождения, что подтверждается результатами, представленными на рисунках 5 и 6.

Оптимизация Траектории: Искусство Контроля

Оптимизация траектории является ключевым фактором достижения высоких результатов в автономных гонках. Эффективное планирование траектории позволяет минимизировать время прохождения круга за счет точного контроля над положением автомобиля, скоростью и ускорением на протяжении всей дистанции. Процесс оптимизации включает в себя поиск оптимальной последовательности управляющих воздействий, обеспечивающих максимальную скорость и стабильность при прохождении поворотов, прямых участков и других элементов трассы. Алгоритмы оптимизации, такие как метод последовательного квадратичного программирования (SQP) и другие численные методы, используются для решения сложных задач нелинейной оптимизации, учитывающих динамику автомобиля, ограничения на управляющие воздействия и геометрию трассы. Успешная оптимизация траектории требует учета множества факторов, включая характеристики автомобиля, состояние трассы и стратегию гонки.

Параметризация сплайнами и на основе вейвлетов предоставляет гибкие методы представления и оптимизации траекторий движения. Сплайны, в частности кубические сплайны, позволяют создавать гладкие кривые, определяемые набором контрольных точек и обеспечивающие непрерывность первой и второй производных, что важно для динамически осуществимых траекторий. Вейвлет-параметризация, в свою очередь, использует вейвлеты — локализованные во времени и частоте функции — для представления траектории, что позволяет эффективно моделировать сложные формы и адаптироваться к изменениям геометрии трассы. Оба подхода позволяют компактно задавать траекторию с помощью небольшого количества параметров, которые затем оптимизируются для достижения максимальной скорости и минимального времени прохождения круга. Выбор конкретного метода зависит от требований к точности, вычислительной сложности и специфики трассы.

Оптимизация по всему горизонту (Full-Horizon Optimization) предполагает планирование траектории с учетом всей длины круга, а не отдельных его сегментов. Такой подход позволяет разрабатывать стратегии, максимизирующие общую производительность, поскольку изменения в одной части трассы могут быть скоординированы с другими. В отличие от локальной оптимизации, где рассматривается лишь небольшой участок, Full-Horizon Optimization учитывает взаимосвязь между всеми участками трассы, что позволяет находить глобально оптимальные решения. Это особенно важно для гонок, где стратегическое планирование и координирование действий на протяжении всего круга критически важны для достижения максимальной скорости и сокращения времени прохождения.

Байесовская оптимизация (BO) представляет собой эффективный метод поиска оптимальных параметров траектории в автономных гонках. В основе этого подхода лежит использование суррогатной модели, ориентированной на конфигурацию трассы (Track-Centric Surrogate Model). Данная модель аппроксимирует сложную функцию, связывающую параметры траектории и время прохождения круга, что позволяет избежать дорогостоящих вычислений, связанных с прямым моделированием динамики автомобиля. BO итеративно уточняет суррогатную модель, используя информацию о результатах предыдущих симуляций или реальных заездов, и затем использует эту модель для выбора наиболее перспективных параметров траектории для следующей итерации. Алгоритм BO эффективно исследует пространство параметров, балансируя между исследованием новых областей и эксплуатацией уже известных, что позволяет быстро сходиться к оптимальным значениям и минимизировать время прохождения круга. Применение BO значительно сокращает количество необходимых симуляций по сравнению с другими методами оптимизации, особенно в задачах с высокой размерностью пространства параметров.

В отличие от традиционных параметризаций траекторий, вейвлет-подход позволяет более точно воспроизводить различные тренды и эффективно представлять множество образцов вблизи оптимальной траектории даже при ограниченном количестве параметров.
В отличие от традиционных параметризаций траекторий, вейвлет-подход позволяет более точно воспроизводить различные тренды и эффективно представлять множество образцов вблизи оптимальной траектории даже при ограниченном количестве параметров.

Эволюция Системы: Непрерывное Совершенствование

Описанные методы функционируют в рамках итеративной системы обучения, предназначенной для непрерывного совершенствования. Эта система предполагает последовательное выполнение нескольких этапов: сбор данных о результатах движения на трассе, уточнение модели динамики транспортного средства и оптимизация траектории. Повторяя эти шаги, система способна адаптироваться к изменениям условий на трассе и улучшать свои показатели с течением времени. Такой подход позволяет не только достичь конкурентоспособности с профессиональными гонщиками, но и превзойти их, демонстрируя среднее улучшение времени круга на 20.7% в различных сценариях.

Рассматриваемая система функционирует в цикле непрерывного совершенствования, последовательно собирая данные о реальной динамике транспортного средства на трассе. Эти данные используются для уточнения математической модели автомобиля, что позволяет более точно предсказывать его поведение в различных условиях. На основе обновленной модели происходит оптимизация траектории движения, направленная на минимизацию времени прохождения круга. Этот итеративный процесс, включающий сбор данных, перестройку модели и оптимизацию траектории, повторяется многократно, позволяя системе адаптироваться к изменениям на трассе и постоянно повышать эффективность движения. В результате, достигается существенное улучшение характеристик автономного транспортного средства, позволяющее ему демонстрировать результаты, превосходящие показатели опытных гонщиков.

Система, функционирующая в рамках итеративного процесса обучения, демонстрирует способность эффективно преодолевать изменения, возникающие на гоночной трассе, и со временем повышать свои результаты. Благодаря непрерывному анализу данных, полученных в процессе движения, и адаптации к специфическим особенностям каждой трассы — будь то неровности покрытия, изменения угла наклона или особенности конфигурации — модель динамики транспортного средства постоянно совершенствуется. Такой подход позволяет системе не только компенсировать непредсказуемые факторы, влияющие на скорость и устойчивость, но и оптимизировать траекторию движения, что в конечном итоге приводит к стабильному улучшению показателей и позволяет ей адаптироваться к новым, ранее не встречавшимся условиям.

Предложенный подход открывает возможности для автономных транспортных средств не просто конкурировать, но и превосходить профессиональных гонщиков на гоночных трассах. В ходе испытаний, система продемонстрировала среднее улучшение времени круга на 20.7% в различных сценариях, что свидетельствует о значительном потенциале для оптимизации траекторий и адаптации к меняющимся условиям. Такой результат достигнут благодаря непрерывному обучению и совершенствованию модели динамики автомобиля, позволяя автономному транспортному средству эффективно справляться с особенностями каждой трассы и демонстрировать превосходство в скорости и точности управления.

Экспериментальные данные показывают, что хорошо настроенный контроллер обеспечивает значительно более быстрое время круга по сравнению с плохо настроенным.
Экспериментальные данные показывают, что хорошо настроенный контроллер обеспечивает значительно более быстрое время круга по сравнению с плохо настроенным.

Исследование демонстрирует, что подход к оптимизации траектории, ориентированный на конкретную трассу, позволяет значительно повысить эффективность обучения автономных гоночных автомобилей. Авторы предлагают не просто абстрактные алгоритмы, а систему, способную адаптироваться к уникальным особенностям каждого трека, что подчеркивает важность учета контекста. Как заметил Эдсгер Дейкстра: «Простота — это предварительное условие надежности». В данном случае, упрощение задачи за счет фокусировки на конкретной трассе, а не на универсальной модели, позволяет достичь большей стабильности и предсказуемости поведения автомобиля. Особенно примечательно применение волновой параметризации и байесовской оптимизации для обучения модели динамики автомобиля непосредственно на трассе, что позволяет учитывать даже незначительные отклонения и нелинейности.

Что Дальше?

Предложенный подход, фокусирующийся на адаптации к специфике трассы, не устраняет, а лишь маскирует фундаментальную проблему — хрупкость оптимизированных систем. Каждая итерация обучения, каждое уточнение динамической модели — это еще один слой зависимости, еще одна потенциальная точка отказа. Система, стремящаяся к идеальному времени круга, становится все более чувствительной к малейшим отклонениям от ожидаемого поведения. Разделение задачи оптимизации траектории и модели динамики — это разделение ответственности, но не судьбы. Когда-нибудь, и оптимизированная траектория, и выученная модель, и сама трасса придут к синхронному коллапсу.

Вместо бесконечного уточнения моделей, возможно, стоит обратить внимание на робастность. Как создать систему, которая не стремится к совершенству, а принимает неизбежность неопределенности? Как построить алгоритм, который не боится отклонений, а адаптируется к ним? Вероятностные модели и байесовская оптимизация — это шаги в правильном направлении, но они лишь смягчают проблему, не решая ее.

В конечном итоге, гонка — это не только оптимизация времени круга, но и выживание. И система, стремящаяся к абсолютному контролю, может оказаться менее приспособленной к реальным условиям, чем система, способная к самоорганизации и адаптации. Изучение принципов устойчивости и самовосстановления может оказаться более перспективным направлением, чем бесконечная гонка за эффективностью.

Оригинал статьи: https://arxiv.org/pdf/2601.21027.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-31 03:30