Оптимальное распределение агентов: новый подход к управлению покрытиями

от

Автор: Денис Аветисян

Исследование предлагает инновационный метод управления группой агентов для эффективного покрытия изменяющейся территории, основанный на принципах оптимального транспорта.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал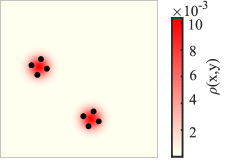
В ходе исследования продемонстрировано, что система из 88 агентов способна поддерживать заданную структуру при изменяющейся плотности, адаптируясь к её сжатию, расширению и даже разделению на бимодальное распределение в моменты времени t=1, t=2, t=4 и t=6 условных единиц.
В ходе исследования продемонстрировано, что система из 88 агентов способна поддерживать заданную структуру при изменяющейся плотности, адаптируясь к её сжатию, расширению и даже разделению на бимодальное распределение в моменты времени t=1, t=2, t=4 и t=6 условных единиц.

В статье разработан фреймворк оптимального транспорта для управления покрытием в многоагентных системах с переменной плотностью, использующий расстояние Вассерштейна и ячейки Лагерра.

Традиционные алгоритмы управления группой агентов для обеспечения покрытия, как правило, ориентированы на статические плотности целей, что ограничивает их применение в динамически меняющихся условиях. В данной работе, посвященной ‘Optimal Transport for Time-Varying Multi-Agent Coverage Control’, предложена новая формулировка задачи, основанная на теории оптимального транспорта, позволяющая агентам минимизировать расстояние Вассерштейна до непрерывно меняющейся целевой плотности. Предложенное решение опирается на связанную систему дифференциальных уравнений, описывающих положение агентов и двойственные переменные, определяющие области Лаггера. Каковы перспективы масштабирования предложенного подхода для задач с большим числом агентов и высокой размерностью пространства?

Элегантность Покрытия: Вызов Динамичной Среды

Эффективное управление покрытием — координация автономных агентов для оптимального сбора данных — играет ключевую роль в широком спектре приложений, от мониторинга окружающей среды и сельскохозяйственного сектора до поисково-спасательных операций и обеспечения безопасности. Точное и полное покрытие территории или объема позволяет своевременно обнаруживать изменения, выявлять аномалии и принимать обоснованные решения. Например, в сельском хозяйстве, рои дронов, скоординированные для покрытия полей, способны оперативно оценивать состояние посевов, выявлять очаги заболеваний или нехватку влаги, что позволяет оптимизировать использование ресурсов и повысить урожайность. В контексте экологического мониторинга, подобные системы позволяют отслеживать распространение загрязнений, контролировать состояние лесов и водных ресурсов. Таким образом, координация группы агентов для достижения оптимального сенсорного покрытия является фундаментальной задачей, определяющей эффективность и результативность множества современных технологических решений.

Традиционные методы управления группой агентов для обеспечения оптимального покрытия сталкиваются с серьезными трудностями в динамически меняющихся условиях. При изменении плотности объектов наблюдения, существующие алгоритмы вынуждены постоянно перестраивать планы действий каждого агента, что требует значительных вычислительных ресурсов и времени. Необходимость непрерывной перепланировки приводит к замедлению реакции системы на изменения в окружающей среде и снижению эффективности покрытия, особенно в сценариях с быстро меняющимися условиями. Постоянный пересчет оптимальных позиций агентов представляет собой существенную проблему с точки зрения масштабируемости и энергопотребления, ограничивая применимость этих подходов в реальных задачах, где требуется оперативное и эффективное покрытие больших территорий.

Существенным ограничением в системах управления группой агентов является их неспособность оперативно адаптировать свои позиции к быстро меняющимся условиям окружающей среды, что негативно сказывается на эффективности работы. Традиционные алгоритмы часто сталкиваются с задержками в перепланировании маршрутов и перераспределении ресурсов, особенно в ситуациях, когда плотность объектов наблюдения динамически изменяется. Неспособность агентов быстро реагировать на такие изменения приводит к ухудшению качества собираемых данных, увеличению времени отклика и, в конечном итоге, к снижению общей производительности системы. Данная проблема особенно актуальна в сложных и непредсказуемых средах, где требуется высокая степень гибкости и адаптивности для поддержания оптимального покрытия наблюдаемой области.

Оценка расхождения между желаемым и фактическим распределением сенсорного покрытия имеет основополагающее значение для эффективного контроля в динамически меняющихся условиях. В рамках представленной работы, для количественной оценки этого расхождения активно используется метрика Кульбака-Лейблера D_{KL}. Продемонстрировано, что разработанная система контроля позволяет достигать значительно более низких значений D_{KL}, что напрямую коррелирует с повышенной точностью отслеживания объектов в сложных, динамичных сценариях. Низкое значение расхождения указывает на то, что фактическое покрытие максимально приближено к оптимальному, обеспечивая надежный сбор данных и эффективное решение поставленных задач. Данный подход позволяет агентам адаптивно перестраивать свое положение, минимизируя погрешности и повышая общую производительность системы.

Предложенный метод успешно отслеживает изменяющиеся во времени гауссовы распределения различной сложности (одномодальные и многомодальные) в одномерном пространстве, демонстрируя более высокую точность (измеряемую расстоянием Вассерштейна) по сравнению с альтернативными подходами, такими как метод на основе диаграмм Вороного и стратегии без прямой связи ([22]), как показано на эволюции плотностей и траекторий агентов.
Предложенный метод успешно отслеживает изменяющиеся во времени гауссовы распределения различной сложности (одномодальные и многомодальные) в одномерном пространстве, демонстрируя более высокую точность (измеряемую расстоянием Вассерштейна) по сравнению с альтернативными подходами, такими как метод на основе диаграмм Вороного и стратегии без прямой связи ([22]), как показано на эволюции плотностей и траекторий агентов.

Оптимальный Транспорт: Основа Управления Покрытием

Оптимальная транспортировка (OT) представляет собой мощный математический аппарат для сравнения вероятностных распределений и определения минимальной стоимости перемещения «массы» между ними. В рамках OT, задача формулируется как поиск оптимального плана транспортировки, минимизирующего общую стоимость перемещения массы из одного распределения в другое, где стоимость определяется функцией расстояния между точками в пространстве. Формально, для двух вероятностных распределений μ и ν на пространстве X, оптимальный план транспортировки γ представляет собой вероятностное распределение на X \times X, которое минимизирует функционал стоимости \in t_{X \times X} c(x, y) d\gamma(x, y), где c(x, y) — функция стоимости транспортировки массы из точки x в точку y. Этот подход позволяет количественно оценить «разницу» между распределениями и найти наиболее эффективный способ преобразования одного в другое.

Применение оптимального транспорта (OT) к задаче управления покрытием позволяет рассматривать агентов как дискретные точки в пространстве, а желаемую плотность покрытия — как непрерывное целевое распределение вероятностей. В данном контексте, агенты представляют собой источники покрытия, распределенные по области, а целевое распределение определяет требуемую плотность покрытия в каждой точке этой области. Задача управления покрытием сводится к определению оптимального расположения агентов, минимизирующего «стоимость» перемещения «массы» от целевого распределения к распределению, определяемому позициями агентов. Математически, это выражается как решение задачи оптимального транспорта, где «стоимость» перемещения может быть определена как расстояние между точками или другая метрика, отражающая эффективность покрытия.

Полудискретный оптимальный транспорт (Semi-Discrete Optimal Transport) представляет собой усовершенствованный метод, позволяющий сравнивать непрерывное целевое распределение плотности с дискретным набором агентов. В отличие от классического оптимального транспорта, требующего сравнения двух непрерывных распределений, полудискретный подход позволяет напрямую вычислять оптимальное размещение агентов для приближения к заданному распределению. Это достигается путем минимизации транспортной стоимости перемещения «массы» от каждого агента к целевому распределению, что приводит к более эффективным вычислениям и практической применимости в задачах управления покрытием. Такой подход упрощает процесс оптимизации, поскольку необходимо учитывать только дискретные позиции агентов, а не непрерывное поле.

Диаграммы Лагерра обеспечивают разделение области покрытия на ячейки влияния, каждая из которых связана с конкретным агентом. Принцип построения диаграммы основан на вычислении расстояния до ближайшего агента для каждой точки в области. Это позволяет определить границы каждой ячейки, формируя разбиение пространства. Использование диаграмм Лагерра упрощает расчет транспортной стоимости в задачах оптимального транспорта, поскольку стоимость перемещения ‘массы’ между ячейками может быть определена на основе геометрии этих ячеек и расстояния между их центрами. Вместо вычисления стоимости перемещения между всеми точками и агентами, расчет сводится к определению стоимости перемещения между ячейками, что существенно снижает вычислительную сложность алгоритма.

Предложенный метод успешно валидирован в одномерных средах с 55 агентами, взаимодействующими только с ближайшими соседями, демонстрируя сходимость эмпирического распределения к целевому, что подтверждается эволюцией плотности агентов (отображенной цветом от белого к красному) и траекториями агентов (черные линии) во времени и пространстве, а также показателями расстояния Вассерштейна (panel b).
Предложенный метод успешно валидирован в одномерных средах с 55 агентами, взаимодействующими только с ближайшими соседями, демонстрируя сходимость эмпирического распределения к целевому, что подтверждается эволюцией плотности агентов (отображенной цветом от белого к красному) и траекториями агентов (черные линии) во времени и пространстве, а также показателями расстояния Вассерштейна (panel b).

Непрерывная Адаптация: Расширение Рамок

Непрерывно-временной полудискретный оптимальный транспорт (Continuous-Time Semi-Discrete Optimal Transport) расширяет стандартную формулировку, позволяя учитывать изменяющиеся во времени целевые плотности распределения. Это достигается за счет включения временной зависимости в функцию стоимости, что позволяет агентам адаптировать свое покрытие в ответ на динамические изменения в целевой плотности. В отличие от статических методов оптимального транспорта, данная методика обеспечивает возможность непрерывной адаптации к изменяющимся условиям, что критически важно для задач, требующих динамического контроля покрытия, например, в задачах мониторинга, робототехники и распределенных сенсорных сетей. Такой подход позволяет агентам реагировать на изменения целевой плотности в реальном времени, оптимизируя распределение ресурсов для обеспечения оптимального покрытия.

Формулировка двойственной задачи Канторовича предоставляет возможность вывести динамику агентов, представляя их движение в виде решений системы дифференциальных уравнений. В рамках данной формулировки, функция стоимости переносится в двойственное пространство, что позволяет выразить оптимальное распределение агентов через градиент этой функции. Полученные дифференциальные уравнения описывают, как каждый агент должен изменять свою позицию во времени, чтобы минимизировать общую стоимость переноса массы к целевой плотности. Решение этих уравнений определяет траектории движения агентов и обеспечивает адаптивное покрытие области в изменяющихся условиях. \frac{d\mathbf{x}_i}{dt} = \nabla_{\mathbf{x}_i} \mathcal{L} , где \mathcal{L} — двойственная лагранжиана, а \mathbf{x}_i — положение i-го агента.

Для децентрализованной реализации алгоритма необходимо вычисление обратной матрицы, что может быть вычислительно затратным. Использование ряда Неймана позволяет эффективно аппроксимировать данную обратную матрицу, значительно снижая вычислительную нагрузку. Ряд Неймана представляет собой бесконечную сумму, которая в данном контексте усекается до определенного порядка для достижения приемлемого компромисса между точностью и вычислительной сложностью. В результате, вычисление обратной матрицы сводится к последовательному умножению матриц, что значительно упрощает процесс и делает его пригодным для реализации на бортовых вычислительных устройствах агентов, избегая необходимости решения сложных систем линейных уравнений.

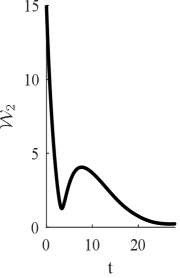
В ходе экспериментов в одномерном пространстве предложенный метод адаптивного оптимального транспорта продемонстрировал значительное снижение метрики Вассерштейна по сравнению с базовыми алгоритмами, такими как основанные на диаграмме Вороного и квазистатический оптимальный транспорт. Конкретно, полученные результаты показывают, что предложенный подход обеспечивает более эффективное распределение агентов и более точное следование за изменяющейся целевой плотностью, что подтверждается количественным анализом W_1-дистанции. Наблюдаемое улучшение производительности указывает на преимущества использования непрерывно-временной адаптации для задач управления покрытием в динамических средах.

На графике показано, что предложенная TV-OT стратегия демонстрирует значительно меньшую ошибку Вассерштейна [latex] (log scale) [/latex] по сравнению с OTCC без прямой связи, при изменении скорости смещения плотности и коэффициента усиления [latex] K_x(y) [/latex].
На графике показано, что предложенная TV-OT стратегия демонстрирует значительно меньшую ошибку Вассерштейна (log scale) по сравнению с OTCC без прямой связи, при изменении скорости смещения плотности и коэффициента усиления K_x(y) .

Уточнение Динамики Агентов с Продвинутым Управлением

Включение пропорциональной обратной связи в контур управления агентами позволяет минимизировать расхождение между текущим положением агента и желаемым положением, вычисленным на основе решения оптимального транспорта. Данный механизм корректировки непрерывно измеряет отклонение агента от целевой точки и генерирует управляющий сигнал, пропорциональный величине этой ошибки. Это обеспечивает плавное и точное приближение агента к заданным координатам, эффективно уменьшая погрешность отслеживания траектории. По сути, пропорциональная обратная связь действует как самокорректирующая система, гарантируя, что агенты остаются на оптимальных путях, определенных алгоритмом оптимального транспорта, даже при наличии внешних возмущений или неточностей в моделировании.

Компенсация по каналу предвидения играет ключевую роль в повышении точности движения агентов. Данный подход позволяет заранее учитывать изменения целевой позиции, корректируя траектории движения еще до возникновения ошибки отслеживания. Вместо реактивного исправления отклонений, система активно прогнозирует будущие потребности в перемещении, что значительно снижает задержки и повышает общую эффективность работы. Фактически, агенты не просто следуют за изменяющейся целью, но и предвосхищают её движение, обеспечивая плавное и точное позиционирование. Это особенно важно в динамических средах, где целевая позиция может быстро меняться, позволяя поддерживать оптимальную производительность и минимизировать погрешности даже при сложных сценариях.

В основе точного и скоординированного движения агентов лежит использование барицентрических координат Лаггера. Эти точки, вычисляемые на основе оптимального транспортного плана, служат ключевыми ориентирами для каждого агента, определяя желаемое положение в пространстве. Вместо непосредственного следования за целевыми точками, агенты стремятся к этим барицентрическим координатам, что позволяет существенно снизить вычислительную сложность и обеспечить более плавные траектории. Laguerre Barycenters эффективно распределяют агентов в пространстве, минимизируя перекрытия и максимизируя покрытие, а также способствуют коллективной координации, позволяя агентам согласованно перемещаться к своим назначениям и избегать столкновений. Такой подход обеспечивает не только высокую точность позиционирования, но и устойчивость системы к внешним возмущениям и изменениям в окружающей среде.

Разработанная система управления покрытием демонстрирует высокую устойчивость и эффективность благодаря интеграции передовых методов контроля. Особым достижением является то, что средняя квадратичная ошибка Вассерштейна, характеризующая отклонение фактического покрытия от оптимального, масштабируется как 1/N, где N — количество агентов. Такая закономерность соответствует теоретическим предсказаниям оптимальной теории квантования, что подтверждает эффективность предложенного подхода к управлению роем агентов и гарантирует достижение высокой точности покрытия при увеличении числа участников. Данный результат указывает на то, что система способна эффективно распределять агентов для минимизации ошибок и достижения оптимального покрытия пространства, даже в сложных и динамически меняющихся условиях.

Исследование демонстрирует, что эффективное управление многоагентными системами требует не просто фиксации структуры, но и понимания динамики их взаимодействия. Авторы предлагают подход, основанный на оптимальном транспорте, позволяющий минимизировать расстояние Вассерштейна между распределением агентов и целевой плотностью. Это подчеркивает важность целостного взгляда на систему, где поведение рождается из взаимодействия компонентов. Как говорил Джон Дьюи: «Образование — это не подготовка к жизни; образование — это сама жизнь». Этот принцип находит отражение в предложенном методе, поскольку он позволяет агентам адаптироваться к изменяющейся среде, обеспечивая эффективное покрытие в динамических условиях.

Куда Дальше?

Представленная работа демонстрирует элегантность подхода оптимального транспорта к задаче покрытия, избегая излишней сложности, присущей традиционным методам, основанным на диаграммах Вороного. Однако, кажущаяся простота этой конструкции не должна вводить в заблуждение. Необходимо признать, что минимизация расстояния Вассерштейна — это лишь один из инструментов, и его эффективность напрямую зависит от корректной оценки динамики целевой плотности. В реальности, эта плотность редко бывает известна заранее и может изменяться непредсказуемо. Поэтому, ключевой задачей на будущее представляется разработка робастных алгоритмов оценки и прогнозирования этой динамики, а не только оптимизация транспортного плана.

Более того, представленный подход, хотя и эффективен для умеренно большого числа агентов, может столкнуться с вычислительными сложностями при масштабировании на системы, насчитывающие сотни или тысячи участников. Необходимо искать компромиссы между точностью решения и вычислительной эффективностью, возможно, используя приближённые методы или иерархические структуры управления. Простота масштабируется, изощрённость — нет. Очевидно, что зависимость от вычислительных ресурсов — настоящая цена свободы выбора наиболее оптимального плана.

В конечном счёте, истинная ценность данной работы заключается не в конкретном алгоритме, а в смене парадигмы. Хорошая архитектура незаметна, пока не ломается. Предложенный подход открывает новые горизонты для разработки интеллектуальных мультиагентных систем, способных адаптироваться к изменяющимся условиям и эффективно решать сложные задачи покрытия. Следующим шагом должно стать исследование возможности применения данного подхода к более широкому классу задач, требующих распределённого принятия решений.

Оригинал статьи: https://arxiv.org/pdf/2601.21753.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-31 05:10