Баланс спроса и предложения: Алгоритм динамического сопоставления в реальном времени

Автор: Денис Аветисян

Новый подход к управлению ресурсами позволяет оптимизировать сопоставление в динамических системах, учитывая непредсказуемость входящих запросов.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал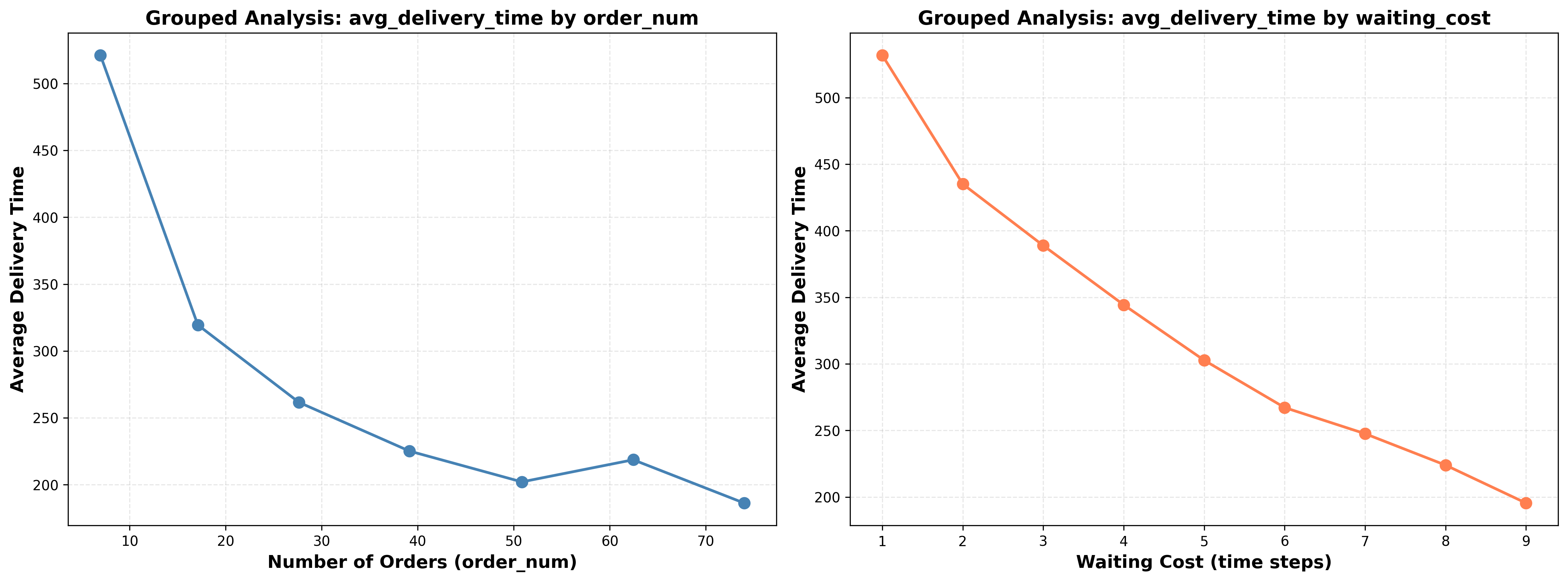

Эмпирическая проверка демонстрирует монотонность стоимости сопоставления, что подтверждает предсказуемость и стабильность алгоритма при различных параметрах и входных данных.

Предлагается алгоритм, обеспечивающий гарантированную производительность в системах динамического сопоставления при неблагоприятных сценариях поступления данных, основанный на принципах балансировки затрат и использующий методы теории массового обслуживания.

Постоянный компромисс между немедленным удовлетворением спроса и ожиданием более эффективных сопоставлений является ключевой проблемой для динамических платформ, от заказа еды до онлайн-игр. В статье ‘When to Match: A Cost-Balancing Principle for Dynamic Markets’ предложен универсальный подход к многостороннему сопоставлению, основанный на принципе балансировки затрат, позволяющий оптимизировать распределение ресурсов в условиях неопределенности. Показано, что разработанный адаптивный алгоритм гарантирует конкурентное соотношение $(1+\sqrt{\Gamma})$ даже при неблагоприятных сценариях поступления запросов, приближаясь к оптимальному решению в реальном времени. Сможет ли этот подход стать основой для построения более эффективных и устойчивых онлайн-платформ в различных отраслях?

Динамическое Сопоставление: Вызовы Реального Времени

Во многих реальных системах возникает необходимость сопоставления агентов с подходящими объектами или задачами в условиях постоянно меняющейся обстановки — этот процесс получил название динамического сопоставления. Данный вид сопоставления отличается от статических моделей тем, что агенты и объекты могут появляться и исчезать, а также изменять свои характеристики со временем. Примерами таких систем являются онлайн-платформы для поиска работы, где кандидаты и вакансии постоянно обновляются, или системы управления транспортом, где необходимо оперативно назначать водителей на рейсы, учитывая меняющиеся дорожные условия и запросы пассажиров. Эффективное динамическое сопоставление играет ключевую роль в оптимизации работы подобных систем и достижении максимальной производительности.

Традиционные алгоритмы сопоставления, такие как жадный алгоритм (GreedyPolicy), зачастую ориентированы исключительно на немедленную выгоду, игнорируя долгосрочные последствия. Данный подход, хотя и обеспечивает быстрые результаты в краткосрочной перспективе, может привести к неоптимальной производительности системы в целом. Например, быстрое назначение агента к первому доступному заданию может заблокировать его от более важных или выгодных задач в будущем, снижая общую эффективность работы системы. В результате, несмотря на кажущуюся рациональность, приоритет мгновенного результата часто оказывается контрпродуктивным, требуя разработки более сложных стратегий, учитывающих временной горизонт и потенциальные выгоды от ожидания.

Суть сложности динамического сопоставления заключается в постоянном компромиссе между выгодой от ожидания более подходящего соответствия и затратами от немедленного выбора, который может оказаться не оптимальным. Системы, требующие оперативного распределения ресурсов или назначения задач, сталкиваются с необходимостью оценки этой дилеммы в режиме реального времени. Задержка в надежде на появление лучшего варианта может привести к упущенным возможностям или увеличению общих издержек, тогда как поспешное решение, хотя и быстрое, может снизить эффективность всей системы. Таким образом, эффективные стратегии динамического сопоставления должны учитывать не только текущую выгоду, но и долгосрочные последствия каждого принимаемого решения, находя баланс между немедленной реакцией и стратегическим ожиданием.

Определение Оптимального Подхода: Политики, Основанные на Затратах

Оптимальная политика (OptimalPolicy) представляет собой идеальный процесс принятия решений, направленный на минимизацию совокупной стоимости ожидания и сопоставления в динамической системе сопоставления. Данная политика определяет, когда следует инициировать процесс сопоставления, учитывая компромисс между затратами на ожидание агентов в очереди и затратами, связанными с самим процессом сопоставления. Минимизация общей стоимости достигается путем балансировки между поддержанием достаточно короткой очереди для снижения $WaitingCost$ и избежанием слишком частых и дорогостоящих процессов сопоставления, влияющих на $MatchingCost$ . Эффективная реализация OptimalPolicy требует точной оценки этих затрат и динамической адаптации стратегии принятия решений к изменяющимся условиям системы.

Взаимосвязь между длиной очереди (QueueLength), стоимостью ожидания (WaitingCost) и стоимостью сопоставления (MatchingCost) является ключевой для определения оптимальной политики в динамической системе сопоставления. Увеличение длины очереди напрямую ведет к росту стоимости ожидания для агентов, поскольку время ожидания возрастает. Однако, более длинная очередь также может снизить стоимость сопоставления, поскольку увеличивается вероятность найти подходящего партнера без необходимости немедленного поиска и связанных с этим затрат. Оптимальная политика должна учитывать компромисс между этими двумя факторами, находя баланс, который минимизирует суммарные затраты, определяемые как $TotalCost = WaitingCost + MatchingCost$ . Анализ этой взаимосвязи позволяет разработать стратегию, которая эффективно управляет очередью и снижает общие издержки системы.

Анализ предельных состояний (FluidLimitAnalysis) представляет собой математический аппарат, используемый для исследования поведения динамической системы согласования при увеличении числа агентов. Данный подход позволяет аппроксимировать дискретную систему непрерывной, что упрощает анализ и позволяет получить аналитические результаты, недоступные при прямом рассмотрении дискретной модели. В рамках анализа предельных состояний, поведение системы описывается дифференциальными уравнениями, которые позволяют определить оптимальную политику принятия решений, минимизирующую суммарные затраты на ожидание и согласование. В частности, анализ позволяет определить оптимальное значение порога, при котором агент переходит из состояния ожидания в состояние активного поиска, учитывая взаимосвязь между длиной очереди, стоимостью ожидания и стоимостью согласования. $\lim_{n \to \in fty} \frac{X_n}{n} = X$ , где $X_n$ — случайная величина, представляющая длину очереди, а $X$ — ее предельное значение.

Балансировка Затрат: Адаптивная Стратегия Сопоставления

Метод CostBalancing представляет собой адаптивную политику, разработанную для оптимизации динамического сопоставления путем динамического балансирования затрат на ожидание и сопоставление. В отличие от статических политик, CostBalancing непрерывно корректирует свои решения на основе текущего состояния системы, стремясь минимизировать общие затраты. Это достигается путем оценки компромисса между затратами на ожидание (связанными с поддержанием элементов в очереди) и затратами на сопоставление (связанными с немедленным выполнением сопоставления). Адаптивность метода позволяет ему эффективно функционировать в условиях изменяющихся объемов запросов и различных затрат, обеспечивая оптимальное сопоставление ресурсов в режиме реального времени.

Метод CostBalancing калибрует процесс принятия решений на основе показателя CostRatio — отношения между стоимостью ожидания и стоимостью сопоставления в оптимальном стационарном состоянии. Этот показатель, $CostRatio = \frac{c_w}{c_m}$ , где $c_w$ — стоимость ожидания, а $c_m$ — стоимость сопоставления, определяет баланс между задержкой и немедленным сопоставлением. Постоянная переоценка CostRatio позволяет алгоритму динамически адаптироваться к изменяющимся условиям, стремясь минимизировать общую стоимость, учитывая как затраты на ожидание, так и затраты на немедленное сопоставление. Использование CostRatio обеспечивает возможность эффективной настройки параметров алгоритма без необходимости предварительного знания характеристик входящего потока запросов.

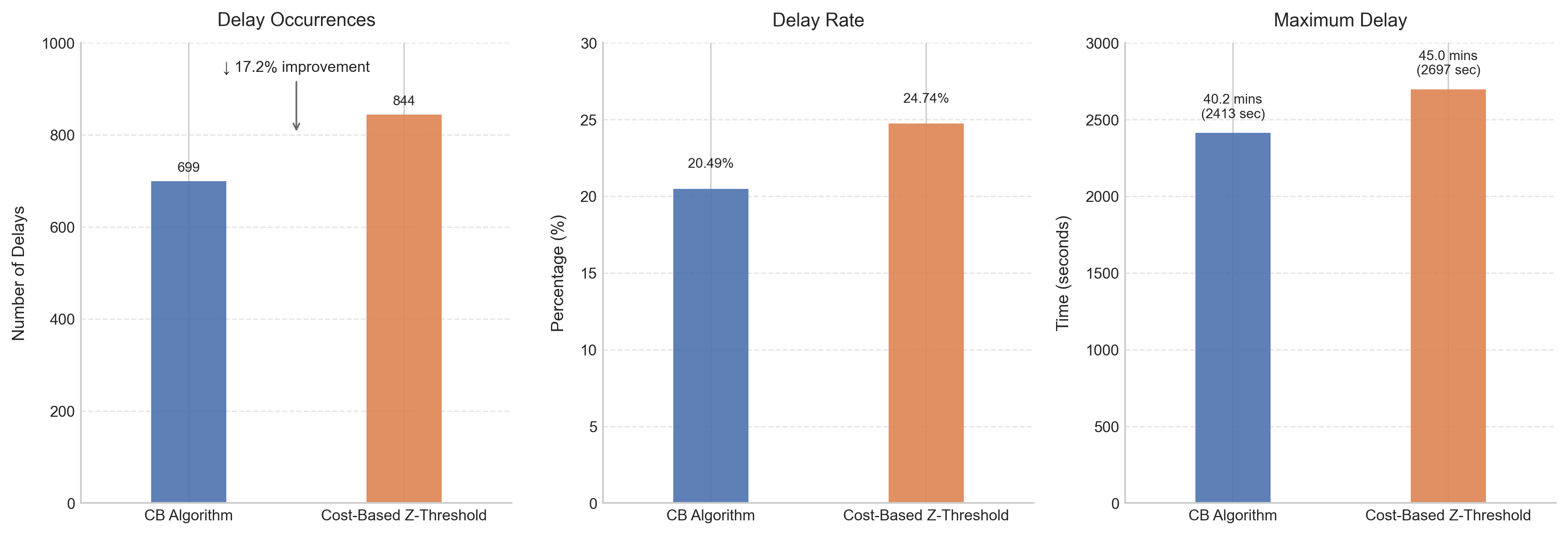
Метод CostBalancing использует информацию о длине очереди (QueueLength) для достижения производительности, близкой к теоретической Оптимальной Политике (OptimalPolicy) в реальном времени. Гарантированный коэффициент конкурентоспособности (competitive ratio) при неблагоприятных сценариях поступления запросов (adversarial arrivals) составляет $(1+Γ)(1+\sqrt{Γ})$ , где Γ представляет собой параметр, характеризующий соотношение между стоимостью ожидания и стоимостью сопоставления. Использование данных о длине очереди позволяет динамически адаптировать стратегию сопоставления, минимизируя общие затраты и обеспечивая предсказуемую производительность даже в условиях изменяющейся нагрузки.

Сравнение производительности показывает, что алгоритм CB превосходит метод Z-порогового значения на основе стоимости.

Надежность в Условиях Нагрузки: Оценка Пределов Производительности

Для оценки эффективности алгоритма CostBalancing используется показатель, известный как CompetitiveRatio — мера, сравнивающая наихудшую производительность алгоритма с оптимальным решением. Данный показатель позволяет определить, насколько сильно алгоритм отстает от идеального сценария в самых сложных ситуациях. Вычисление CompetitiveRatio предполагает сравнение общей стоимости, которую несет алгоритм, с минимально возможной стоимостью, которую можно было бы достичь при наличии полной информации о будущих событиях. Чем ближе значение CompetitiveRatio к единице, тем эффективнее алгоритм, поскольку он приближается к оптимальному решению даже в неблагоприятных условиях. Именно этот показатель служит ключевым критерием для оценки надежности и практической применимости алгоритма CostBalancing в задачах оптимизации.

Для всесторонней оценки алгоритма CostBalancing применяются так называемые “враждебные прибытия” (AdversarialArrivals) — специально сконструированные последовательности поступления задач, направленные на максимизацию его стоимости. Такой подход позволяет подвергнуть алгоритм суровому испытанию, выявляя его пределы производительности в наиболее неблагоприятных условиях. В отличие от случайных или усредненных сценариев, “враждебные прибытия” гарантируют, что алгоритм будет протестирован на его самых слабых местах, что обеспечивает более надежную и точную оценку его эффективности и устойчивости. Этот метод позволяет установить нижнюю границу конкурентного соотношения, равную золотому сечению ( $\approx 1.618$ ), для любого онлайн-алгоритма в рассматриваемой задаче.

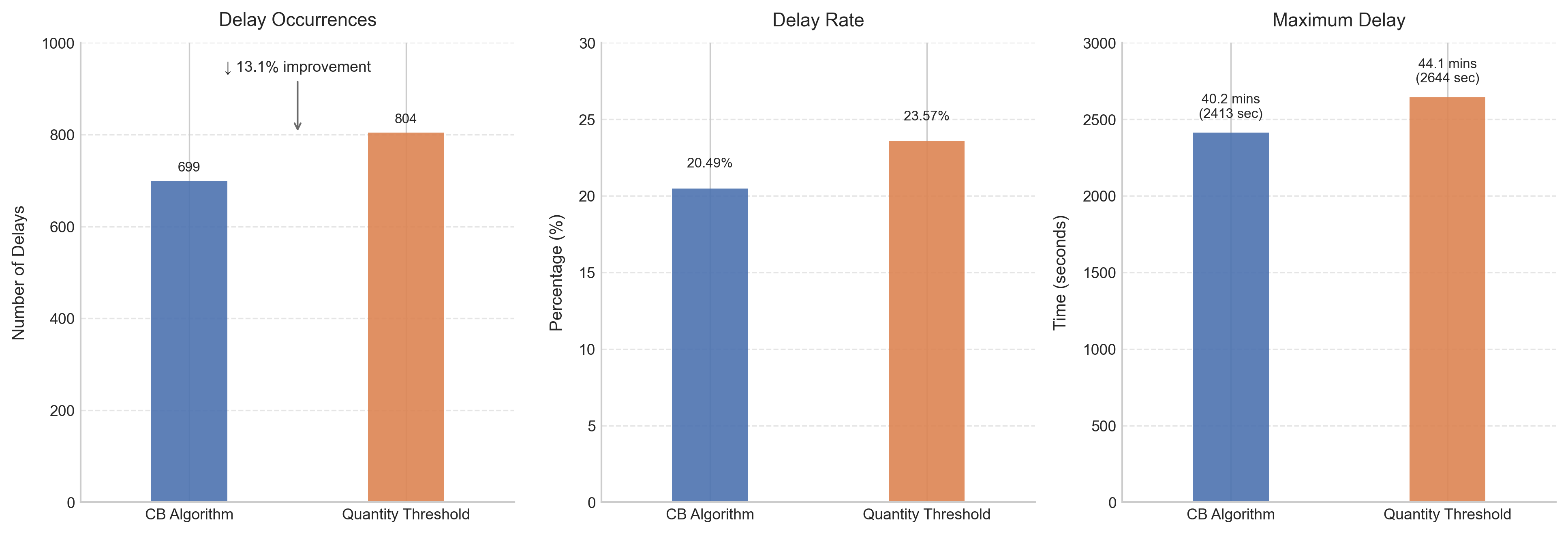
Исследования показали высокую практическую эффективность алгоритма CostBalancing в сложных условиях эксплуатации. В ходе тестирования, алгоритм достиг конкурентного соотношения $(1+Γ)(1+\sqrt{Γ})$ , что свидетельствует о его способности находить решения, близкие к оптимальным, даже при намеренно неблагоприятных сценариях поступления данных. Более того, полученные результаты установили нижнюю границу для конкурентного соотношения любого онлайн-алгоритма в данной задаче — число золотого сечения (приблизительно 1.618). Это означает, что CostBalancing не просто эффективен сам по себе, но и задает планку производительности, которую трудно превзойти другим алгоритмам, работающим в режиме реального времени и без предварительной информации о будущих данных.

Алгоритм CB демонстрирует превосходство над пороговым методом, обеспечивая более высокую производительность.

Исследование, представленное в данной работе, демонстрирует важность поиска баланса между немедленной выгодой и долгосрочными затратами в динамических системах. Принцип, лежащий в основе предложенного алгоритма, находит отражение в известном высказывании Альберта Эйнштейна: «Не стремитесь к успеху, стремитесь к ценностям, которые делают успех возможным». Подобно тому, как алгоритм оптимизирует распределение ресурсов, учитывая как текущие, так и будущие издержки, Эйнштейн подчеркивает необходимость ориентироваться на фундаментальные принципы, а не на сиюминутные достижения. Особенно важно, что алгоритм гарантирует производительность даже при неблагоприятных условиях, что подчеркивает устойчивость системы и её способность адаптироваться к изменениям внешней среды — ключевой аспект, который разделяет предложенный подход и фундаментальные принципы, заложенные в научном наследии Эйнштейна.

Куда Далее?

Представленный анализ принципа балансировки затрат в динамических системах сопоставления, несомненно, открывает новые пути для исследований, но и обнажает ряд вопросов. Строгость доказательств, гарантирующих производительность алгоритма при неблагоприятных условиях, подталкивает к изучению более сложных моделей поступления задач. Представленные предельные теоремы, хоть и элегантны, всё же оперируют упрощенными предположениями о природе потоков. Какова чувствительность алгоритма к отклонениям от этих предположений? Или, другими словами, где та граница, за которой «баланс» нарушается?

Особый интерес представляет расширение концепции балансировки затрат на системы с более сложной структурой — например, с множеством гетерогенных ресурсов или с учетом временной стоимости ресурсов. Наблюдается закономерная тенденция к усложнению моделей, но не всегда понятно, оправдано ли это с практической точки зрения. Ведь истинная ценность теории заключается не в её абстрактной красоте, а в её способности решать реальные задачи.

Следующим шагом видится разработка алгоритмов, способных адаптироваться к меняющимся условиям в реальном времени, учитывая не только текущие затраты, но и предсказывая будущие. Ошибки в прогнозах неизбежны, но именно они и являются источником понимания. По сути, необходимо создать систему, которая учится на своих ошибках и совершенствуется со временем — задача, не лишенная иронии, но, безусловно, достойная внимания.

Оригинал статьи: https://arxiv.org/pdf/2601.21858.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-01 06:31