Эволюция без задач: Новый подход к адаптивной оптимизации

Автор: Денис Аветисян

Исследователи представили алгоритм ABOM, способный самостоятельно совершенствовать стратегии оптимизации, не требуя предварительного обучения на специализированных задачах.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал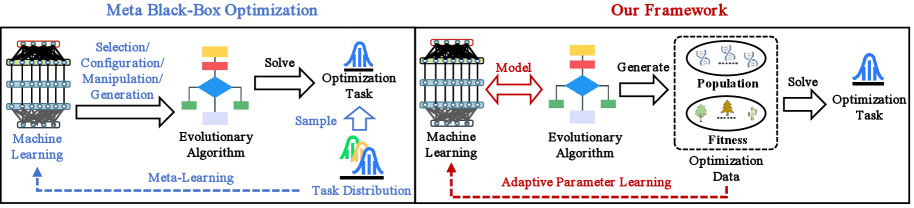

Методы MetaBBO учатся мета-стратегиям на основе распределения задач, но полагаются на разработанные вручную тренировочные данные, в то время как предлагаемая система осуществляет адаптивное обучение параметров, используя самогенерируемые данные оптимизации, что позволяет избежать зависимости от конкретного распределения задач.

Алгоритм ABOM, использующий адаптивное обучение параметров эволюционных операторов, демонстрирует передовые результаты в задачах чёрного ящика и градиент-свободной оптимизации.

Эффективность стандартных оптимизаторов быстро снижается при решении сложных задач чёрного ящика. В данной работе, посвященной задаче ‘Task-free Adaptive Meta Black-box Optimization’, предложена модель ABOM, реализующая мета-оптимизацию без предварительного обучения на размеченных задачах. Ключевой особенностью является адаптивное изменение параметров эволюционных операторов непосредственно в процессе оптимизации целевой функции, что позволяет достичь конкурентоспособных результатов на синтетических и реальных задачах, включая планирование траектории беспилотных летательных аппаратов. Каким образом предложенный подход может быть масштабирован для решения еще более сложных и многомерных задач оптимизации в различных областях науки и техники?

Вызов «Черного Ящика»: Преодолевая Неизвестность в Оптимизации

Во многих практических задачах, от проектирования сложных инженерных систем до разработки новых материалов и финансовых моделей, оптимизация сводится к поиску наилучших значений параметров для функции, которая описывает желаемый результат. Однако, часто возникает ситуация, когда аналитическое выражение для этой функции либо неизвестно, либо слишком сложно для вычисления ее производных. Это создает серьезную проблему, поскольку традиционные методы оптимизации, такие как градиентный спуск, полагаются именно на информацию о производных для эффективного поиска оптимального решения. В подобных случаях, когда функция представляется как «черный ящик» — то есть, известны только входные данные и соответствующие выходные значения — применяются специальные методы, известные как оптимизация «черного ящика». Именно эта неспособность использовать информацию о производных делает задачу оптимизации особенно сложной и требует разработки альтернативных, более устойчивых и адаптивных алгоритмов.

Традиционные методы оптимизации, такие как градиентный спуск или метод Ньютона, зачастую сталкиваются с серьезными трудностями при работе с задачами высокой размерности. По мере увеличения числа переменных, пространство поиска решения экспоненциально расширяется, что требует колоссальных вычислительных ресурсов и времени для достижения приемлемого результата. Кроме того, вычисление производных, необходимых для этих методов, может быть невозможным или крайне затратным, особенно в случае “черных ящиков”, где внутренняя структура функции неизвестна. Это приводит к замедлению сходимости алгоритмов, увеличению риска попадания в локальные оптимумы и, в конечном итоге, к неэффективности в решении сложных оптимизационных задач, что обуславливает необходимость разработки альтернативных, более устойчивых подходов.

В условиях оптимизации “черных ящиков”, когда аналитическое выражение функции отсутствует или ее вычисление связано с огромными затратами, потребность в устойчивых и адаптивных стратегиях становится первостепенной. Исследования показывают, что стандартные методы оптимизации часто терпят неудачу в многомерных пространствах, требуя подходов, способных эффективно исследовать и использовать информацию о целевой функции даже при ее непредсказуемом поведении. Разработка алгоритмов, которые могут динамически корректировать свою стратегию поиска в зависимости от особенностей ландшафта оптимизации, представляется критически важной для достижения эффективных и надежных решений в широком спектре практических задач — от проектирования сложных систем до машинного обучения и финансовых моделей. Особое внимание уделяется алгоритмам, способным избегать локальных оптимумов и находить глобальные решения, несмотря на шум и неопределенность, свойственные реальным задачам.

Алгоритм ABOM использует адаптивный цикл оптимизации, включающий инициализацию, размножение, оценку, элитизм и адаптацию параметров, а для размножения применяются эволюционные операторы на основе внимания, такие как отбор, кроссовер и мутация.

Мета-Оптимизация: Автоматизация Оптимизатора

Мета-оптимизация, или “обучение оптимизации”, представляет собой подход, позволяющий автоматически разрабатывать алгоритмы оптимизации, адаптированные к конкретным классам задач. В отличие от традиционных методов, где алгоритм и его параметры задаются вручную, мета-оптимизация использует алгоритмы машинного обучения для поиска оптимальной стратегии оптимизации. Этот процесс включает в себя анализ характеристик целевой задачи и автоматическую генерацию или выбор наиболее подходящего алгоритма и его гиперпараметров. Результатом является алгоритм, специализированный для эффективного решения задач определенного типа, что потенциально обеспечивает более высокую производительность и снижает потребность в ручной настройке.

Адаптивная мета-оптимизация расширяет концепцию автоматического проектирования алгоритмов оптимизации, позволяя им динамически изменять свои стратегии непосредственно в процессе оптимизации. В отличие от традиционных методов, требующих предварительной настройки параметров и статических алгоритмов, адаптивные подходы используют обратную связь от процесса оптимизации для корректировки параметров алгоритма или даже выбора различных операторов оптимизации в режиме реального времени. Это позволяет алгоритмам адаптироваться к сложным и меняющимся ландшафтам оптимизации, повышая их робастность и эффективность без необходимости ручной настройки или предварительного знания структуры задачи. Такой подход особенно полезен в задачах, где характеристики целевой функции неизвестны или изменяются во времени.

Использование адаптивной мета-оптимизации позволяет отказаться от ручной настройки параметров алгоритма, что значительно упрощает процесс оптимизации и снижает трудозатраты. Вместо этого, алгоритм самостоятельно корректирует свои стратегии в процессе работы, адаптируясь к особенностям решаемой задачи. Это обеспечивает устойчивую производительность и надежные результаты даже в условиях разнообразных и сложных ландшафтов оптимизации, где традиционные методы с фиксированными параметрами могут демонстрировать нестабильное или неоптимальное поведение. Автоматическая адаптация повышает общую надежность и эффективность процесса оптимизации в широком спектре прикладных задач.

Анализ чувствительности показал, что производительность алгоритма на наборе BBOB существенно зависит от размера популяции (NN), скрытой размерности ([latex]d_M[/latex]), вероятности отбрасывания при кроссовере ([latex]p_C[/latex]) и вероятности отбрасывания при мутации ([latex]p_M[/latex]), в то время как анализ влияния скорости обучения представлен в Приложении I. — Анализ чувствительности показал, что производительность алгоритма на наборе BBOB существенно зависит от размера популяции (NN), скрытой размерности ( $d_M$ ), вероятности отбрасывания при кроссовере ( $p_C$ ) и вероятности отбрасывания при мутации ( $p_M$ ), в то время как анализ влияния скорости обучения представлен в Приложении I.

ABOM: Дифференцируемый Эволюционный Фреймворк

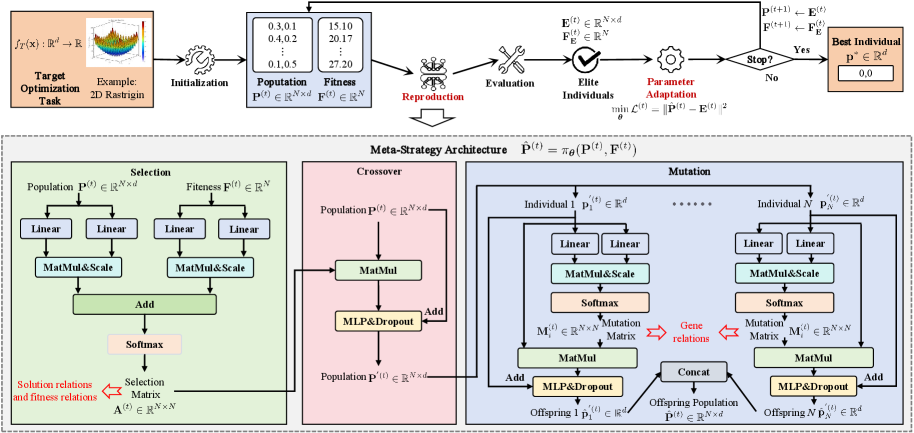
ABOM представляет собой мета-оптимизатор, не требующий постановки конкретной задачи, использующий дифференцируемые эволюционные операторы. Это позволяет оптимизировать стратегии оптимизации посредством градиентного спуска. В отличие от традиционных эволюционных алгоритмов, ABOM оперирует с непрерывными, дифференцируемыми функциями для операций отбора, скрещивания и мутации, что делает возможным вычисление градиентов и применение стандартных методов оптимизации, таких как $\nabla_{\theta} L(\theta)$ , где θ — параметры стратегии оптимизации, а $L$ — функция потерь, оценивающая эффективность данной стратегии. Такой подход позволяет ABOM адаптировать и улучшать стратегии оптимизации непосредственно на основе градиентной информации, минуя необходимость в дискретном поиске и эвристических правилах.

В основе ABOM лежат три основных компонента: отбор (Selection), кроссовер (Crossover) и мутация (Mutation), каждый из которых реализован посредством дифференцируемых функций. Это позволяет вычислять градиенты через весь процесс эволюции, что обеспечивает эффективную адаптацию стратегий оптимизации. Дифференцируемый отбор позволяет оценивать вклад каждого индивида в следующее поколение с учетом его приспособленности и других факторов. Дифференцируемый кроссовер позволяет плавно комбинировать генетический материал родителей, создавая новые решения. Дифференцируемая мутация вносит небольшие, контролируемые изменения в генетический код, способствуя исследованию пространства поиска. Использование дифференцируемых функций в этих компонентах является ключевым для применения методов градиентного спуска для оптимизации всей эволюционной стратегии.

Модель ABOM использует механизмы внимания (Attention Mechanisms) для эффективного моделирования взаимосвязей между особями в популяции, характеристиками ландшафта пригодности (fitness landscape) и генетическими компонентами. Эти механизмы позволяют модели динамически взвешивать важность различных особей и генетических признаков при принятии решений о селекции, кроссовере и мутации. В частности, внимание применяется для оценки влияния каждого гена на пригодность особи, а также для выявления корреляций между генами и ландшафтом пригодности. Это позволяет модели более эффективно адаптировать стратегии оптимизации к сложным задачам, выявляя и усиливая полезные генетические комбинации и игнорируя неэффективные.

Элитный архив (EliteArchive) в рамках ABOM выполняет функцию сохранения лучших найденных решений на протяжении всего процесса оптимизации. Этот архив, представляющий собой набор высококачественных особей, обеспечивает защиту от потери перспективных решений, которые могли бы быть утеряны в процессе мутаций или кроссовера. Регулярное добавление новых, превосходящих текущие решения, в архив, а также использование этих решений для направления поиска, способствует более быстрой сходимости алгоритма к оптимальным или суб-оптимальным результатам. Таким образом, элитный архив действует как механизм стабилизации и ускорения обучения, гарантируя, что наиболее эффективные генетические стратегии не будут случайно отброшены.

Сравнение сходимости алгоритмов ABOM и ABOM-NPA на тестовом наборе BBOB при [latex]d=500[/latex] показывает, что нормализованные затраты уменьшаются по мере увеличения числа вычислений функции, при этом оба алгоритма демонстрируют схожую эффективность на 30 независимых запусках. — Сравнение сходимости алгоритмов ABOM и ABOM-NPA на тестовом наборе BBOB при $d=500$ показывает, что нормализованные затраты уменьшаются по мере увеличения числа вычислений функции, при этом оба алгоритма демонстрируют схожую эффективность на 30 независимых запусках.

Валидация и Производительность на Бенчмарках

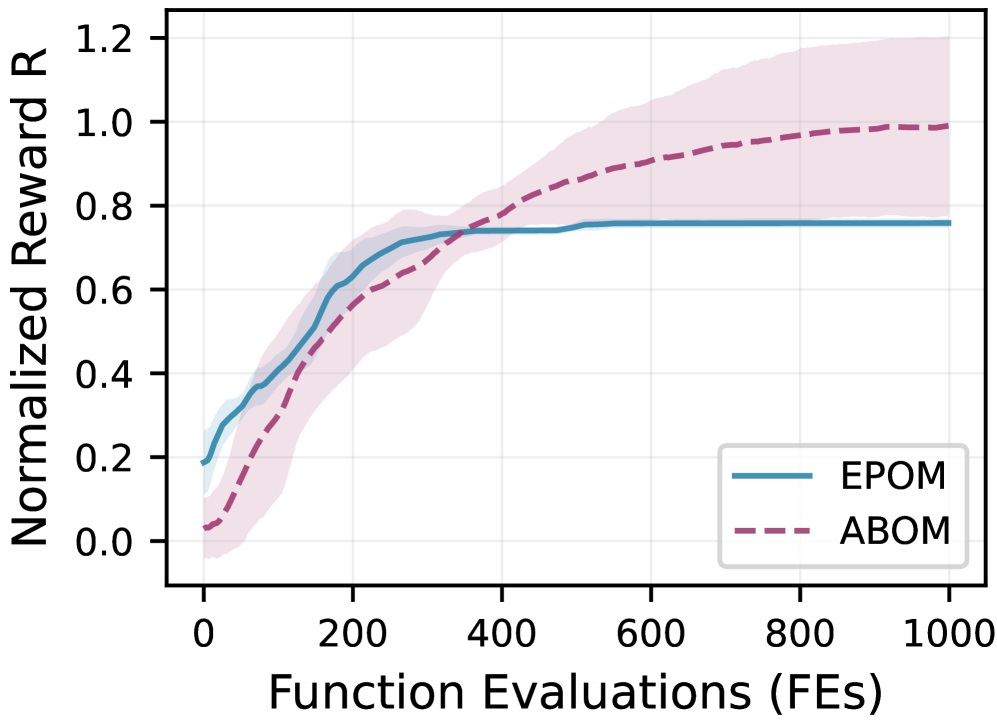
Алгоритм ABOM подвергся всестороннему тестированию на широко известном наборе бенчмарков BBOB, где он продемонстрировал конкурентоспособные, а зачастую и превосходящие результаты по сравнению с передовыми алгоритмами оптимизации. Особенно выделяется скорость сходимости алгоритма на синтетических тестовых задачах, позволяющая находить оптимальные решения значительно быстрее, чем у существующих методов. Полученные данные свидетельствуют о высокой эффективности ABOM в решении широкого спектра задач оптимизации и подтверждают его потенциал для применения в различных областях науки и техники.

Механизм адаптации параметров в алгоритме ABOM, усиленный применением регуляризации методом Dropout, обеспечивает устойчивую и надежную оптимизацию на разнообразных ландшафтах поиска. Этот подход позволяет алгоритму эффективно адаптироваться к различным характеристикам целевой функции, предотвращая переобучение и поддерживая стабильность процесса оптимизации даже в сложных и многомерных пространствах. Применение Dropout способствует формированию более робастных моделей параметров, которые менее чувствительны к шуму и локальным оптимумам, что в конечном итоге приводит к повышению качества и надежности полученных решений на различных тестовых задачах и реальных приложениях.

Алгоритм ABOM демонстрирует высокую эффективность в исследовании сложных поисковых пространств, что напрямую влияет на скорость сходимости и качество получаемых решений. Способность быстро адаптироваться к особенностям ландшафта целевой функции позволяет алгоритму избегать локальных оптимумов и находить более оптимальные решения по сравнению с традиционными методами. Это особенно заметно при решении задач высокой размерности и задач с множеством ограничений, где традиционные алгоритмы часто сталкиваются с трудностями. Эффективное перемещение по сложному пространству параметров обеспечивает не только более быструю сходимость, но и стабильность процесса оптимизации, что подтверждается результатами тестирования на различных бенчмарках.

Алгоритм ABOM демонстрирует более быструю сходимость по сравнению с EPOM при обучении агента для задачи Bipedal Walker.

Применение и Перспективы Развития

Адаптивность алгоритма ABOM делает его особенно ценным инструментом для решения сложных задач оптимизации, в частности, в области планирования маршрутов беспилотных летательных аппаратов (БПЛА). В этой сфере, где требуется находить эффективные и безопасные траектории полёта, учитывая множество факторов — от препятствий и погодных условий до ограничений по энергопотреблению — способность ABOM к быстрой адаптации к меняющимся обстоятельствам является ключевым преимуществом. В отличие от традиционных методов, которые часто требуют значительных вычислительных ресурсов и времени для пересчета маршрута при возникновении новых препятствий, ABOM способен оперативно корректировать траекторию полёта, обеспечивая более надёжное и эффективное выполнение поставленной задачи. Это особенно важно в динамичных средах, где БПЛА должен реагировать на непредсказуемые изменения в реальном времени, например, при облёте строительных площадок или проведении поисково-спасательных операций.

Особенностью ABOM является его дифференцируемая структура, что позволяет беспрепятственно интегрировать его с другими методами машинного обучения. Такая совместимость открывает широкие возможности для инноваций, позволяя использовать ABOM в качестве компонента более сложных систем. Например, его можно объединить с нейронными сетями для обучения с подкреплением или использовать в гибридных подходах, сочетающих символьные и статистические методы. Благодаря дифференцируемости, градиенты могут распространяться через ABOM, что делает возможным оптимизировать всю систему “end-to-end”, повышая общую производительность и адаптируемость к новым задачам. Это свойство делает ABOM не просто отдельным алгоритмом, а гибким строительным блоком для создания более интеллектуальных и эффективных решений в различных областях.

Дальнейшие исследования направлены на расширение возможностей алгоритма ABOM для решения задач повышенной сложности, включая сценарии, требующие обработки огромных объемов данных и учета множества взаимосвязанных факторов. Особый интерес представляет изучение потенциала ABOM в области автоматизированного машинного обучения (AutoML), где он может быть использован для автоматического проектирования и оптимизации моделей машинного обучения, значительно упрощая и ускоряя процесс создания интеллектуальных систем. Предполагается, что гибкость и эффективность ABOM позволят автоматизировать рутинные этапы разработки моделей, высвобождая ресурсы для более творческих и сложных задач, и, в конечном итоге, способствуя развитию новых поколений самообучающихся систем.

Анализ матриц отбора и мутации алгоритма ABOM на функциях BBOB ([latex]f_4[/latex], [latex]f_{11}[/latex], и [latex]f_{24}[/latex] при [latex]d=30[/latex]) показывает, как алгоритм адаптирует стратегии отбора и мутации на протяжении эволюции (поколения 1, 500 и 1000). — Анализ матриц отбора и мутации алгоритма ABOM на функциях BBOB ( $f_4$ , $f_{11}$ , и $f_{24}$ при $d=30$ ) показывает, как алгоритм адаптирует стратегии отбора и мутации на протяжении эволюции (поколения 1, 500 и 1000).

Представленное исследование демонстрирует элегантность подхода к мета-оптимизации, избегая необходимости в ручном проектировании обучающих задач. Алгоритм ABOM, основанный на адаптивном обучении параметров эволюционных операторов, подчеркивает важность целостного взгляда на систему. Барбара Лисков однажды заметила: «Хорошие дизайнеры стремятся к простоте, но не упрощению». Эта фраза прекрасно отражает суть работы — стремление к эффективному решению за счет изящной структуры, а не за счет усложнения. Успех ABOM в различных бенчмарках подтверждает, что понимание взаимосвязей внутри системы и адаптация к изменяющимся условиям являются ключом к созданию устойчивых и эффективных алгоритмов.

Куда Далее?

Представленный подход, хотя и демонстрирует впечатляющие результаты в адаптации эволюционных операторов без привязки к конкретным задачам, не избавляет от фундаментальной дилеммы: любое упрощение неизбежно влечёт за собой потери. Автоматическое обучение, как и любая эвристика, оперирует с ограниченным представлением о пространстве решений. Вопрос не в том, чтобы создать алгоритм, «решающий всё», а в понимании границ его применимости и потенциальных искажений, вносимых адаптацией.

Перспективы дальнейших исследований, по-видимому, лежат в плоскости интеграции мета-оптимизации с более глубоким пониманием структуры ландшафта оптимизации. Следует изучить возможности использования полученных знаний об адаптивных операторах для разработки более эффективных стратегий исследования пространства, возможно, сочетающих преимущества эволюционных алгоритмов с градиентными методами там, где это уместно. Особый интерес представляет вопрос о переносе знаний между различными классами задач — насколько универсальными могут быть адаптивные операторы, и какие механизмы необходимы для их эффективной адаптации к новым условиям?

В конечном счёте, важно помнить, что алгоритм — это лишь инструмент. Элегантность решения заключается не в сложности, а в простоте и ясности структуры, определяющей поведение системы. Поиск оптимальной структуры — задача, требующая не только вычислительных ресурсов, но и глубокого понимания принципов, лежащих в основе оптимизации.

Оригинал статьи: https://arxiv.org/pdf/2601.21475.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-01 21:35