Безопасное обучение с подкреплением: Гарантии в условиях риска

Автор: Денис Аветисян

Новый подход к обучению агентов позволяет минимизировать потенциальные убытки и гарантировать соблюдение заданных ограничений в сложных средах.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Анализ производительности алгоритма EcoAnt демонстрирует, что VaR-CPO, PPO, CPO и CPPO обеспечивают различную степень соблюдения ограничений в зависимости от начального размера батареи (50 и 500), при этом, согласно результатам, полученным за 5 и 10 миллионов временных шагов и подтвержденным стандартным отклонением по пяти случайным инициализациям, VaR-CPO демонстрирует наиболее стабильное соблюдение ограничений даже при неблагоприятных начальных условиях.

В статье представлена методика VaR-CPO, использующая неравенство Чебышёва для оптимизации обучения с подкреплением с учётом Value-at-Risk и интеграции в фреймворк CPO.

Обеспечение безопасности и надежности в обучении с подкреплением остается сложной задачей, особенно в критически важных приложениях. В данной работе представлена методика ‘Value-at-Risk Constrained Policy Optimization’, предлагающая новый подход к оптимизации стратегий с учетом ограничений на Value-at-Risk (VaR). Используя неравенство Чебышева для аппроксимации VaR и интегрируя его в структуру Constrained Policy Optimization (CPO), авторы добились строгих гарантий в отношении нарушения ограничений в процессе обучения. Сможет ли предложенный алгоритм VaR-CPO стать основой для разработки более безопасных и предсказуемых систем обучения с подкреплением в реальных условиях?

Необходимость Ограниченной Оптимизации в Обучении с Подкреплением

Обучение с подкреплением демонстрирует впечатляющие результаты в решении сложных задач, однако зачастую пренебрегает вопросами безопасности, что может приводить к неприемлемым рискам при внедрении в реальные системы. Несмотря на способность агентов оптимизировать поведение для достижения поставленной цели, стандартные алгоритмы не содержат встроенных механизмов, гарантирующих соблюдение заданных ограничений. Например, робот, обученный максимально быстро выполнять задачу, может игнорировать правила безопасности, приводя к повреждениям оборудования или даже травмам. В критически важных областях, таких как автономное вождение или управление медицинским оборудованием, подобные упущения недопустимы, и требуется разработка специализированных подходов, учитывающих не только эффективность, но и безопасность действий агента.

Традиционные методы обучения с подкреплением, несмотря на свою эффективность в решении сложных задач, не обладают встроенными механизмами для обеспечения соблюдения ограничений и требований безопасности. В ситуациях, где цена ошибки высока, например, в управлении транспортными средствами или роботизированной хирургии, подобное упущение может приводить к недопустимым рискам. Поэтому, для применения обучения с подкреплением в критически важных системах необходимы специализированные техники, позволяющие явно задавать и контролировать соблюдение ограничений в процессе обучения агента. Эти методы направлены на то, чтобы не просто максимизировать награду, но и гарантировать, что действия агента остаются в рамках допустимых и безопасных параметров, предотвращая потенциально опасные ситуации и обеспечивая надежность работы системы.

Для решения проблемы обеспечения безопасности в обучении с подкреплением, необходимо переформулировать процесс обучения в рамках Constrained Markov Decision Process (ограниченного марковского процесса принятия решений). Данный подход позволяет явно включить критерии безопасности в целевую функцию агента, определяя не только желаемую награду, но и допустимые границы для выполнения действий. Вместо простого максимизирования награды, агент стремится оптимизировать ее, строго соблюдая заданные ограничения, что гарантирует предотвращение нежелательных или опасных состояний. По сути, это означает, что процесс обучения направлен на поиск оптимальной стратегии, которая обеспечивает максимальную производительность, не нарушая при этом установленные рамки безопасности, что критически важно для применения в реальных, чувствительных к рискам системах.

Value-at-Risk: Строгий Инструмент Ограничения Риска

Ограничение по величине риска (Value-at-Risk, VaR) представляет собой строгий метод ограничения вероятности превышения определенного порогового значения убытков. Это достигается путем определения максимального уровня убытков, который не будет превышен с заданной вероятностью в течение определенного периода времени. Например, VaR в размере 10 миллионов рублей с уровнем доверия 95% означает, что существует лишь 5% вероятность того, что убытки превысят 10 миллионов рублей в течение указанного периода. Данный подход обеспечивает надежную гарантию безопасности, позволяя количественно оценить и контролировать потенциальные финансовые риски и, следовательно, является важным инструментом управления рисками в различных областях, включая финансы, страхование и инвестиции.

Непосредственное применение ограничения Value-at-Risk (VaR) для управления рисками сопряжено со значительными вычислительными трудностями. Это связано с необходимостью точного моделирования распределения вероятностей потенциальных потерь, что может быть нереализуемо для сложных финансовых инструментов или систем. Для преодоления этих сложностей используются суррогатные методы, представляющие собой приближенные решения, позволяющие эффективно оценивать и контролировать риск, сохраняя при этом приемлемый уровень точности. Эти методы, как правило, основаны на статистических оценках и упрощенных моделях, обеспечивающих компромисс между вычислительной эффективностью и точностью прогнозирования. Использование суррогатных методов позволяет практиковать управление рисками в реальном времени, несмотря на сложность исходной задачи.

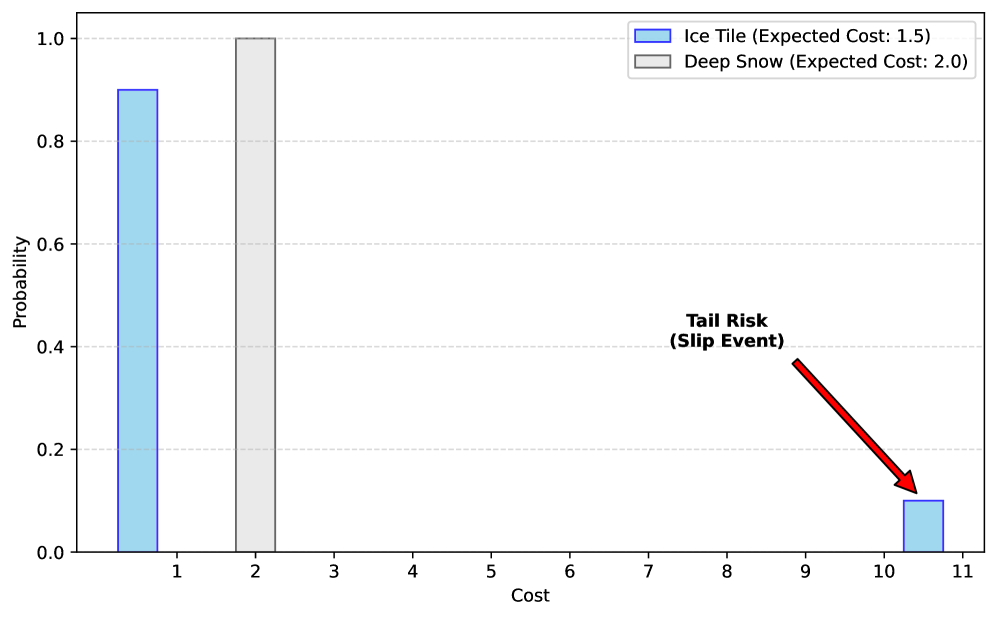
Неравенство Чебышёва предоставляет теоретическую основу для оценки верхней границы кумулятивной стоимости, однако его применение требует осторожности при работе с неотрицательными издержками. В общем виде, неравенство утверждает, что вероятность отклонения случайной величины от её математического ожидания на величину, большую заданной, ограничена сверху. В контексте оценки рисков, это позволяет установить верхнюю границу вероятности превышения определённого порога стоимости. Однако, стандартная форма неравенства Чебышёва может давать консервативные оценки, особенно если стоимость ограничена снизу нулем. Это связано с тем, что неравенство не учитывает асимметрию распределения стоимости и рассматривает как положительные, так и отрицательные отклонения от среднего значения, что не всегда применимо к издержкам. Для более точной оценки в таких случаях требуется адаптация или использование специализированных вариантов, таких как одностороннее неравенство Чебышёва, разработанное специально для неотрицательных случайных величин.

Неравенство Чебышева, применяемое для оценки вероятности превышения определенного порога, может быть недостаточно точным для оценки рисков, связанных с издержками, поскольку не учитывает, что издержки всегда неотрицательны. Одностороннее неравенство Чебышева (P(X \ge a) \le \frac{E[X]}{a}[/latex], где X[/latex] — неотрицательная случайная величина и a > 0[/latex]) обеспечивает более жесткую оценку, поскольку учитывает эту особенность. Это делает его предпочтительным инструментом для определения Value-at-Risk (VaR), поскольку позволяет получить более точную и надежную верхнюю границу для вероятности превышения заданного уровня издержек, что критически важно для управления финансовыми рисками.

Сурогат Чебышева обеспечивает допустимые области VaR при пороге стоимости [latex]\rho = 100[/latex] и вероятности нарушения [latex]\epsilon = 0.05[/latex], однако, в силу своей универсальности для распределений с конечными первым и вторым моментами, он может быть излишне консервативным по сравнению со случаем, когда известно, что распределение стоимости является гауссовским. — Сурогат Чебышева обеспечивает допустимые области VaR при пороге стоимости \rho = 100 и вероятности нарушения \epsilon = 0.05, однако, в силу своей универсальности для распределений с конечными первым и вторым моментами, он может быть излишне консервативным по сравнению со случаем, когда известно, что распределение стоимости является гауссовским.

VaR-CPO: Практический Алгоритм Безопасного Обучения с Подкреплением

Дополнение состояния (State Augmentation) в алгоритме VaR-CPO заключается в расширении вектора состояния агента на величину, отражающую накопленную стоимость эпизода. Это позволяет агенту учитывать прошлые затраты при принятии решений, что критически важно для точной оценки вторых моментов (дисперсии) стоимости, необходимых для реализации суррогатного ограничения. Включение накопленной стоимости эпизода в вектор состояния улучшает оценку риска и позволяет более эффективно контролировать нарушение ограничений в процессе обучения с подкреплением, обеспечивая более безопасное поведение агента.

Алгоритм VaR-CPO реализует интеграцию неравенства Чебышева (одностороннего варианта) в процесс оптимизации политики с ограничениями. Это позволяет напрямую контролировать Value-at-Risk (VaR) — меру максимального ожидаемого убытка с заданной вероятностью. В основе подхода лежит использование неравенства Чебышева для формирования суррогатного ограничения, которое учитывает как ожидаемую стоимость, так и ее дисперсию. В процессе обучения политики, VaR-CPO оптимизирует функцию вознаграждения, гарантируя, что вероятность превышения заданного порога стоимости ограничена. Таким образом, VaR-CPO предоставляет практический метод обеспечения безопасности обучения агента в средах, где критически важно ограничить риски, связанные с накопленной стоимостью эпизода.

Эффективность алгоритма VaR-CPO напрямую зависит от мониторинга максимального нарушения ограничения (Worst-Case Constraint Violation) в процессе обучения. Данное нарушение определяется как функция от ожидаемых затрат (Expected Cost) и дисперсии затрат (Variance of Cost). В ряде тестовых сред VaR-CPO продемонстрировал нулевой уровень нарушения ограничений (Constraint Violation Rate = 0), в отличие от базовых методов, что свидетельствует о его способности обеспечивать более безопасное обучение с подкреплением. Для оценки нарушения используется метрика, позволяющая отслеживать отклонения от установленных ограничений на протяжении всего процесса обучения, что необходимо для гарантии безопасности агента.

Теоретическая оценка нарушения ограничения в алгоритме VaR-CPO выражается формулой 2δγc/(1−γc)2(απk+1C~ + 2απk+1C/ϵ[μ(πk) + απk+1C/(1−γc)])[/latex], где δ[/latex] — допустимый уровень риска, γc[/latex] — коэффициент дисконтирования стоимости, α[/latex] — коэффициент, определяющий скорость обучения, πk+1[/latex> — обновленная политика, C~[/latex> — оценка стоимости, ϵ[/latex> — параметр, влияющий на точность оценки, и μ(πk)[/latex] — ожидаемая стоимость при использовании политики πk[/latex>. Данная формула предоставляет верхнюю границу на вероятность превышения заданного порога стоимости, тем самым гарантируя безопасность агента в процессе обучения с подкреплением и обеспечивая выполнение ограничений на стоимость.

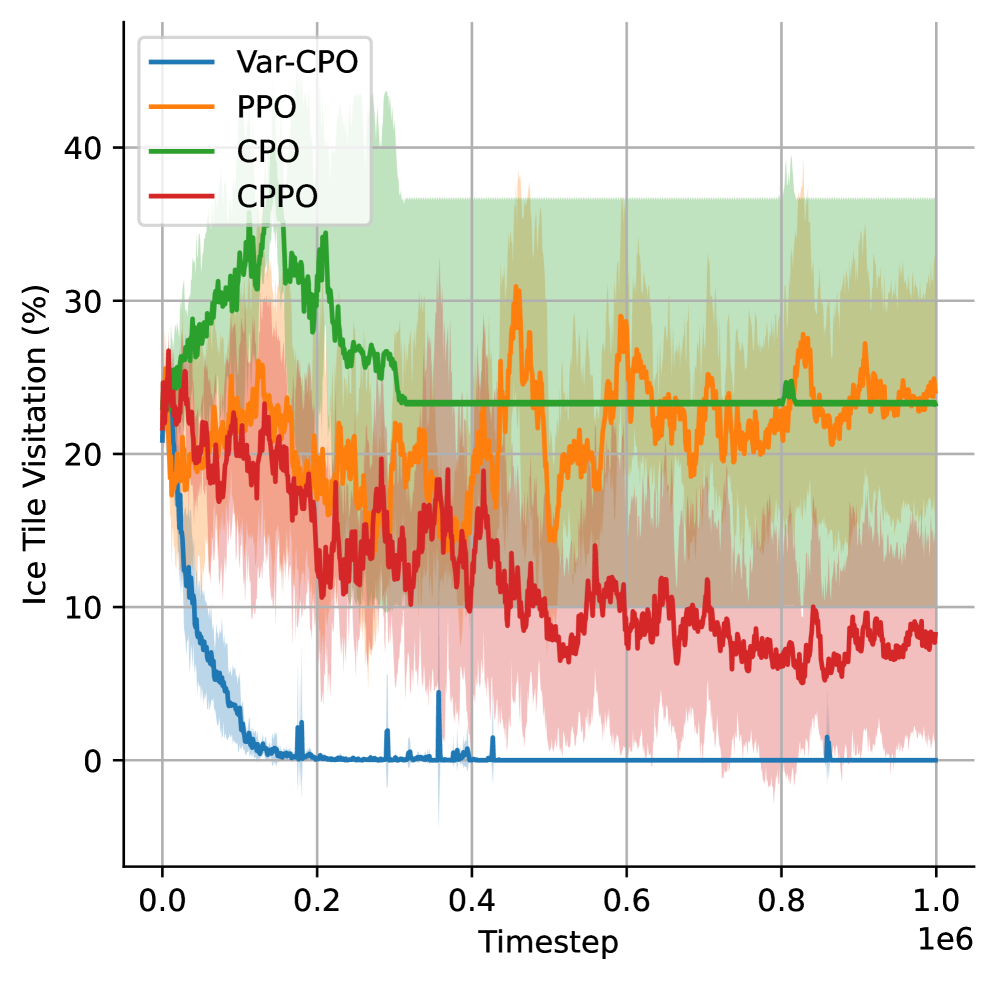
Анализ производительности на среде IcyLake демонстрирует, что VaR-CPO (синий), PPO (оранжевый), CPO (зеленый) и CPPO (красный) сходятся к стабильной награде за первые 10 000 шагов симуляции, при этом затененные области показывают стандартное отклонение по 5 разным начальным условиям.

Подтверждение Эффективности и Широкая Применимость

Эффективность VaR-CPO была подтверждена в различных средах, включая сложные виртуальные миры, такие как “IcyLake” и “EcoAnt”. Данные среды, отличающиеся по динамике и сложности, позволили продемонстрировать способность алгоритма к адаптации и поддержанию высокой безопасности. В “IcyLake”, характеризующейся скользкой поверхностью и непредсказуемым движением, VaR-CPO успешно выбирал более безопасный маршрут, в то время как другие алгоритмы, например PPO и CPO, отдавали приоритет среднему вознаграждению, игнорируя потенциальные риски. Аналогичные результаты были получены в “EcoAnt”, где алгоритм демонстрировал стабильную работу в условиях сложной местности и изменяющихся препятствий. Это подтверждает универсальность VaR-CPO и его применимость к широкому спектру задач обучения с подкреплением, требующих надежной работы в непредсказуемых условиях.

Алгоритм демонстрирует устойчивое и значительное превосходство в обеспечении безопасности и соблюдении ограничений по сравнению с базовыми методами. Исследования показывают, что VaR-CPO не просто стремится к максимальной суммарной награде, но и активно минимизирует риски, что особенно важно в критических ситуациях. Преимущество заключается в способности алгоритма эффективно находить решения, удовлетворяющие заданным ограничениям, даже в сложных и динамичных средах, обеспечивая более надежную и предсказуемую работу по сравнению с подходами, ориентированными исключительно на оптимизацию общей награды. Такой подход позволяет значительно снизить вероятность возникновения нежелательных последствий и повысить общую надежность системы.

В среде “IcyLake”, алгоритм VaR-CPO продемонстрировал способность выбирать более безопасную траекторию движения, в отличие от алгоритмов PPO и CPO, которые отдавали приоритет максимизации средней награды. Это различие подчеркивает, что VaR-CPO эффективно учитывает риски и стремится к избежанию опасных ситуаций, даже если это влечет за собой незначительное снижение общей награды. В то время как PPO и CPO, ориентированные на получение максимальной прибыли в краткосрочной перспективе, могли выбирать более быстрые, но потенциально рискованные пути, VaR-CPO обеспечивал более надежное и предсказуемое поведение, минимизируя вероятность столкновений или падений на скользкой поверхности. Данный подход особенно важен в реальных приложениях, где безопасность является критическим фактором, например, в управлении роботами или автономными транспортными средствами.

Успех разработанного подхода ставит под вопрос эффективность альтернативных методов, в частности, ограничения на основе условного значения в риске (Conditional Value-at-Risk Constraint). В отличие от предложенной системы, подобные подходы зачастую лишены строгих теоретических гарантий и демонстрируют более низкие показатели в практических применениях. Исследования показывают, что ограничение на основе условного значения в риске может приводить к компромиссам между безопасностью и производительностью, в то время как разработанный фреймворк обеспечивает более надежное соблюдение ограничений и существенное повышение безопасности без ущерба для общей эффективности, что делает его более предпочтительным решением в задачах, требующих высокой надежности и предсказуемости.

Распределение вероятностей стоимости состояний в среде IcyLake показывает, как часто встречаются различные уровни затрат при решении задачи.

В представленной работе акцент делается на строгую математическую основу алгоритмов обучения с подкреплением, что находит глубокий отклик в философии Г.Х. Харди. Он говорил: «Математика — это искусство делать очевидные вещи сложным образом». Подобно тому, как VaR-CPO стремится к гарантиям безопасности посредством оптимизации Value-at-Risk с использованием неравенства Чебышёва, Харди подчёркивал необходимость доказательной чистоты. Важность математической строгости, продемонстрированная в исследовании, иллюстрирует, что простое решение не обязательно короткое, оно непротиворечивое и логически завершённое, и именно это обеспечивает надёжность и предсказуемость в сложных системах обучения.

Что Дальше?

Предложенный подход, VaR-CPO, представляет собой логичный шаг к обеспечению безопасности в обучении с подкреплением. Однако, пусть N стремится к бесконечности — что останется устойчивым? Гарантии, основанные на неравенстве Чебышёва, элегантны в своей простоте, но по сути своей являются вероятностными. Вопрос не в том, что алгоритм работает на текущем наборе тестов, а в том, как он поведет себя в условиях, принципиально отличающихся от тех, что были предусмотрены при его разработке. Ограничения, основанные на Value-at-Risk, неизбежно вводят консерватизм; необходимо тщательно исследовать компромисс между безопасностью и производительностью, особенно в задачах, где даже незначительные потери могут быть критическими.

Будущие исследования должны сосредоточиться на преодолении ограничений, присущих вероятностным гарантиям. Возможно, стоит рассмотреть методы, позволяющие получить детерминированные границы на нарушение ограничений, или разработать адаптивные стратегии, которые корректируют ограничения в процессе обучения, основываясь на наблюдаемом поведении агента. Интересным направлением является интеграция VaR-CPO с другими подходами к обеспечению безопасности, такими как формальная верификация и робастное обучение.

В конечном итоге, истинное достоинство любого алгоритма обучения с подкреплением будет определяться не его способностью решать задачи в идеальных условиях, а его надежностью и предсказуемостью в реальном мире. Элегантность математической чистоты не должна затмевать необходимость практической применимости и верификации.

Оригинал статьи: https://arxiv.org/pdf/2601.22993.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-02 14:32