Танцующая волатильность: как корреляция меняет ценообразование экзотических опционов

Автор: Денис Аветисян

Новое исследование показывает, что учет динамической корреляции между ценой актива и его волатильностью значительно повышает точность моделей ценообразования для сложных финансовых инструментов.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал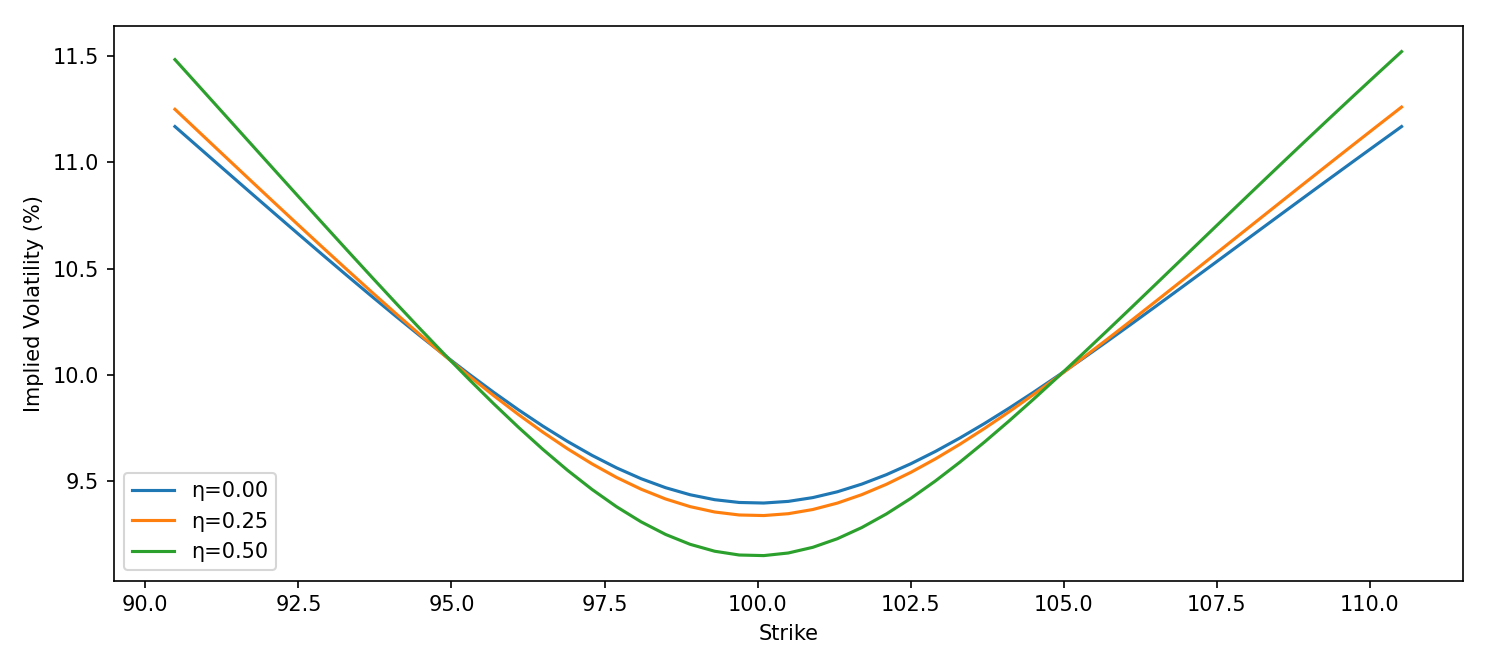

Включение стохастической корреляции между текущей ценой актива и его волатильностью оказывает существенное влияние на подразумеваемую волатильность, что отражает нелинейную взаимосвязь между этими параметрами и указывает на необходимость учета корреляционных эффектов при построении моделей ценообразования опционов.

Расширение стохастической модели волатильности Хестона с учетом стохастической корреляции между ценой и волатильностью для улучшения оценки барьерных опционов и свопов волатильности.

Традиционные модели стохастической волатильности часто не учитывают динамическую взаимосвязь между изменением спотовой цены и волатильности. В работе ‘Keeping Up with the Correlations: Stochastic Spot/Volatility Correlation and Exotic Pricing’ предложена модификация модели Хестона, включающая стохастическую корреляцию спота и волатильности, что позволяет более точно оценивать экзотические опционы и свопы на волатильность. Полученные результаты показывают, что учет этой динамической корреляции существенно влияет на стоимость барьерных опционов и свопов, сопоставимо или даже превышая спред «бид-аск». Не приведет ли дальнейшее развитие данной модели к более адекватному управлению рисками и повышению эффективности ценообразования на финансовых рынках?

Понимание Нестабильности: Ограничения Традиционных Моделей

Точное ценообразование деривативов напрямую зависит от адекватного моделирования волатильности, однако стандартные подходы часто оказываются неспособными уловить всю сложность рыночной динамики. Традиционные модели, основанные на предположении о постоянстве волатильности или ее нормальном распределении, не учитывают такие явления, как асимметрия волатильности и кластеризация волатильных периодов. Это приводит к систематическим ошибкам в оценке стоимости производных финансовых инструментов и создает серьезные риски для управления портфелем. Например, наблюдаемая на практике волатильность опционов «out-of-the-money» значительно превышает волатильность «in-the-money» опционов — явление, известное как «skew», которое игнорируется многими базовыми моделями. Более того, волатильность сама по себе не является статичной величиной, а меняется во времени, реагируя на различные рыночные события и настроения инвесторов, что требует от моделей способности адаптироваться к этим изменениям.

Существующие модели ценообразования деривативов часто сталкиваются с трудностями при адекватном отражении асимметрии волатильности — явления, известного как “skew”. Эта асимметрия проявляется в том, что опционы “out-of-the-money” и “in-the-money” имеют разные подразумеваемые волатильности, что не соответствует предположениям базовых моделей, основанных на нормальном распределении. Более того, характер этой асимметрии не является статичным, а со временем эволюционирует, реагируя на изменения рыночной конъюнктуры и настроений инвесторов. Неспособность моделей точно отразить эту динамику приводит к ошибкам в оценке стоимости производных финансовых инструментов и, как следствие, к неадекватной оценке рисков, что может приводить к значительным финансовым потерям для участников рынка. В частности, при недооценке риска “хвостовых” событий, связанных с резкими колебаниями цен, участники рынка могут оказаться недостаточно защищенными от неблагоприятных сценариев.

В финансовых моделях, используемых для оценки деривативов и управления рисками, мгновенная корреляция между изменением цены актива и его волатильностью играет критически важную роль. Однако, существующие рамки зачастую упрощают этот параметр, рассматривая его как постоянную величину или используя чрезмерно упрощенные предположения. На практике, эта корреляция динамична и чувствительна к рыночным условиям, особенно в периодах стресса. $\rho(t)$ — мгновенная корреляция, может существенно влиять на формирование волатильности и, следовательно, на стоимость опционов. Недооценка этой динамики приводит к неточным оценкам рисков и потенциальным убыткам, особенно при использовании моделей, не учитывающих зависимость между ценой и волатильностью, что делает необходимым разработку более сложных и реалистичных моделей, способных адекватно отражать эту взаимосвязь.

Калибровка параметров демонстрирует зависимость между волатильностью корреляции и точностью настройки.

Модель Хестона: Основа Стохастической Волатильности

Модель Хестона вносит существенное улучшение в моделирование финансовых активов, вводя стохастический процесс волатильности. В отличие от моделей, предполагающих постоянную или детерминированную волатильность, в модели Хестона сама волатильность рассматривается как случайная переменная, изменяющаяся во времени. Это достигается путем моделирования волатильности как квадратного корня из случайного процесса, обычно описываемого с помощью уравнения диффузии. Математически, волатильность $\sigma_t$ подвержена случайным колебаниям, что позволяет более реалистично отразить динамику рыночных цен и, в частности, объяснить феномены, такие как волатильность улыбки и скоса, которые не объясняются простыми моделями. По сути, модель Хестона позволяет волатильности изменяться случайным образом, что делает ее более гибкой и способной к более точному моделированию рыночных данных.

Модель Хесто использует аффинный процесс, что позволяет получить аналитические решения для цен некоторых производных финансовых инструментов. Аффинный процесс предполагает линейную зависимость между ценой актива и его волатильностью, что существенно упрощает вычисления и позволяет избежать численных методов в некоторых случаях. В частности, для европейских опционов колл и пут существуют формулы, выражающие их цену через параметры модели, такие как уровень волатильности, скорость возврата к среднему и коэффициент корреляции. Это, в свою очередь, значительно упрощает процедуру калибровки модели, то есть подбора параметров к наблюдаемым рыночным ценам опционов, по сравнению с моделями, требующими численных методов для определения цены опциона и последующей оптимизации параметров.

Модель Хестона, вводя стохастическую корреляцию между ценой актива и его волатильностью, начинает учитывать сложность волатильности смещения (volatility skew). В отличие от моделей, предполагающих постоянную или детерминированную волатильность, стохастическая корреляция позволяет волатильности реагировать на изменения цены актива и наоборот. Это приводит к более реалистичному описанию рыночных цен опционов, особенно опционов «out-of-the-money» и «in-the-money», для которых наблюдается систематическое отклонение от предсказаний модели Блэка-Шоулза. Величина корреляции, обозначаемая как ρ, является ключевым параметром модели и влияет на форму волатильности смещения, позволяя более точно соответствовать эмпирическим данным.

Разница в ценах при однократном касании, рассчитанная по параметру η, демонстрирует зависимость от модели Хестона.

Калибровка и Валидация Модели: Обеспечение Точности

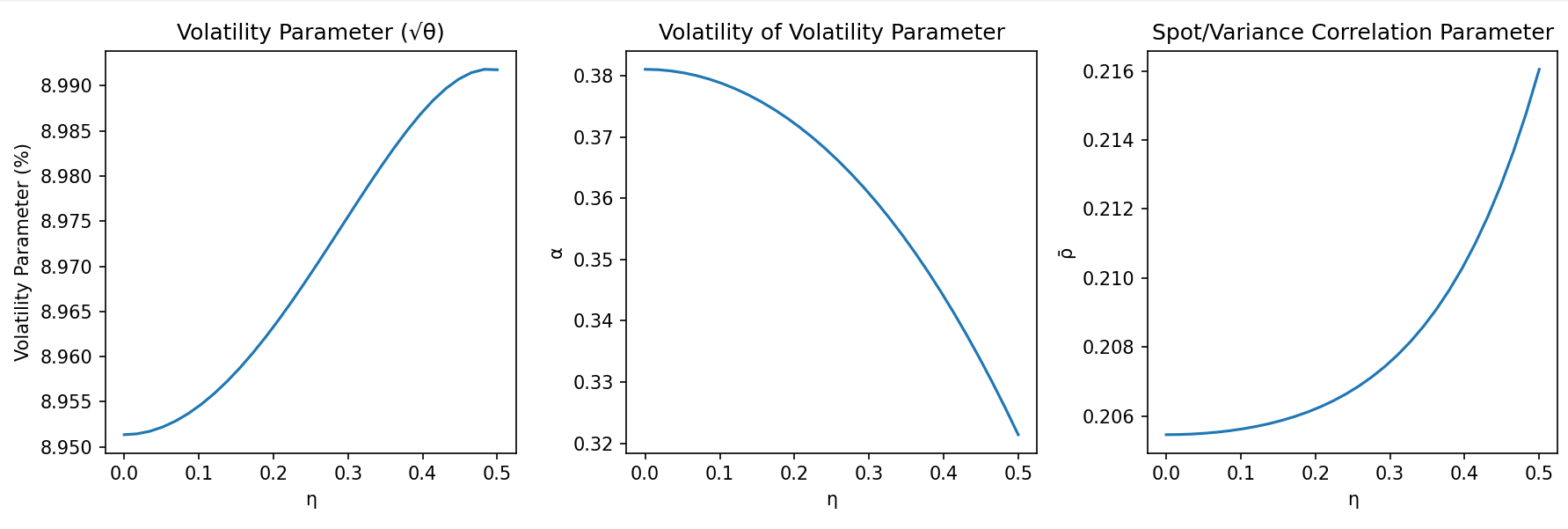
Точная оценка параметров модели имеет решающее значение для успешной реализации, и обычно осуществляется путем калибровки по наблюдаемым ценам европейских ванильных опционов. Этот процесс предполагает подбор значений параметров модели таким образом, чтобы теоретические цены на ванильные опционы соответствовали рыночным ценам. В качестве входных данных используются цены опционов с различными страйками и сроками погашения. Калибровка часто выполняется с использованием численных методов оптимизации, минимизирующих разницу между теоретическими и рыночными ценами. Точность калибровки напрямую влияет на надежность последующего ценообразования и хеджирования более сложных производных инструментов.

Оценка производительности модели требует проверки ее способности к ценообразованию более сложных производных финансовых инструментов, таких как барьерные опционы. В отличие от европейских ванильных опционов, используемых для калибровки, барьерные опционы имеют условия, зависящие от траектории базового актива, что делает их ценообразование более сложной задачей. Точность модели в ценообразовании барьерных опционов является показателем ее способности адекватно отражать динамику рынка и учитывать риски, связанные с более сложными структурами. Неспособность модели корректно оценить барьерные опционы указывает на необходимость ее пересмотра и улучшения.

Метод Монте-Карло представляет собой эффективный инструмент для оценки стоимости сложных производных инструментов, таких как барьерные опционы, где аналитическое решение отсутствует. Процесс включает в себя генерацию большого количества случайных траекторий базового актива и расчет выплаты по инструменту для каждой траектории. Среднее значение этих выплат, дисконтированное к текущему моменту времени, дает оценку стоимости инструмента. Кроме того, Монте-Карло симуляция позволяет проводить валидацию точности модели путём сравнения результатов ценообразования с рыночными данными или альтернативными моделями в различных сценариях изменения параметров, таких как волатильность и процентные ставки. Количество симуляций напрямую влияет на точность оценки, при этом увеличение количества симуляций приводит к уменьшению стандартной ошибки оценки.

Бета реверсии риска модели зависит от срока погашения опциона, что указывает на изменение чувствительности к изменениям волатильности с течением времени.

За пределами Хестона: Улучшение Представления Волатильности

Модель Double Heston расширяет базовую структуру Heston путем введения двух поддисперсий, что позволяет более гибко и детально описывать поверхность подразумеваемой волатильности. В отличие от однофакторной модели Heston, Double Heston позволяет моделировать более сложные формы улыбки волатильности и скоса, поскольку две дисперсии ( $\nu_1$ и $\nu_2$ ) эволюционируют независимо и влияют на динамику волатильности актива. Это особенно полезно для инструментов с более сложными характеристиками зависимости волатильности от страйка и времени экспирации, обеспечивая более точное соответствие рыночным данным и улучшая калибровку модели.

Модель Double Heston, расширяя возможности базовой модели Хестона, повышает точность ценообразования более широкого спектра производных финансовых инструментов за счет более адекватного отражения сложной динамики волатильности. Традиционные модели часто не способны точно описать все особенности имплицитной волатильности, особенно в периоды рыночной нестабильности или при наличии волатильных «улыбок» и «перекосов». Double Heston, используя два параметра суб-дисперсии, позволяет более гибко моделировать эти эффекты, что приводит к снижению ошибок при оценке стоимости опционов и других деривативов. Повышение точности особенно заметно при работе с экзотическими опционами, чувствительными к сложным зависимостям между ценой базового актива и его волатильностью.

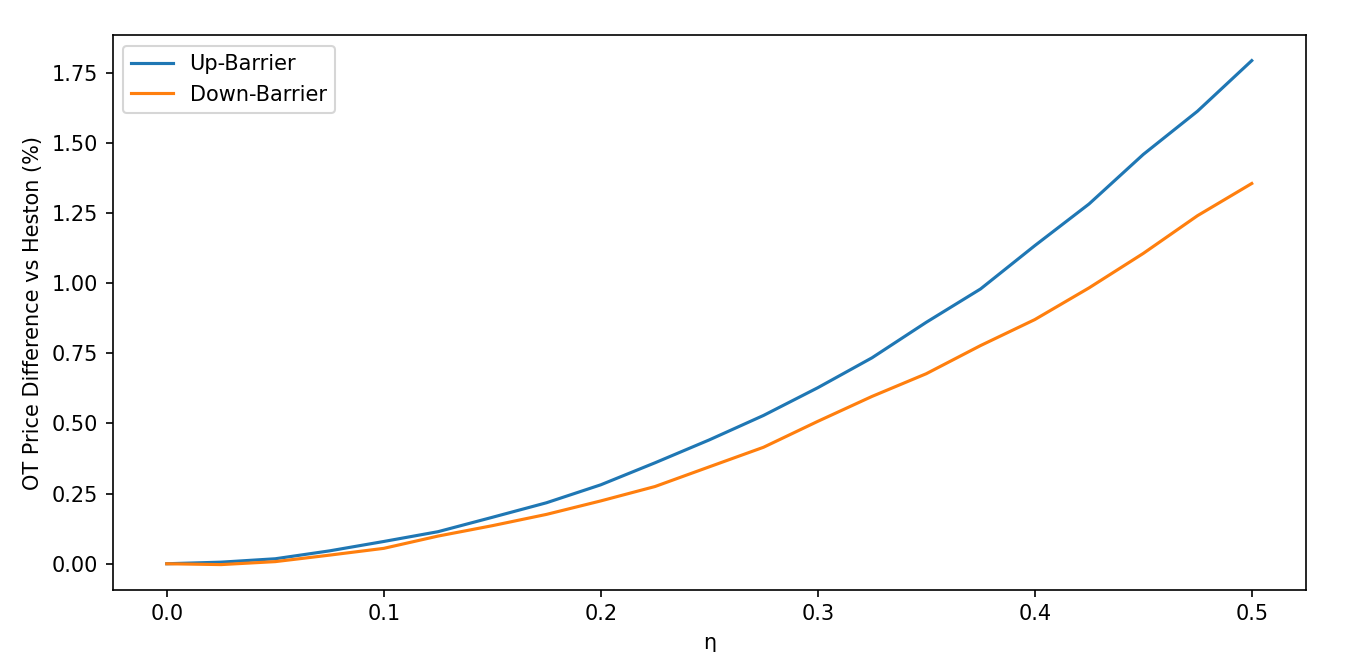
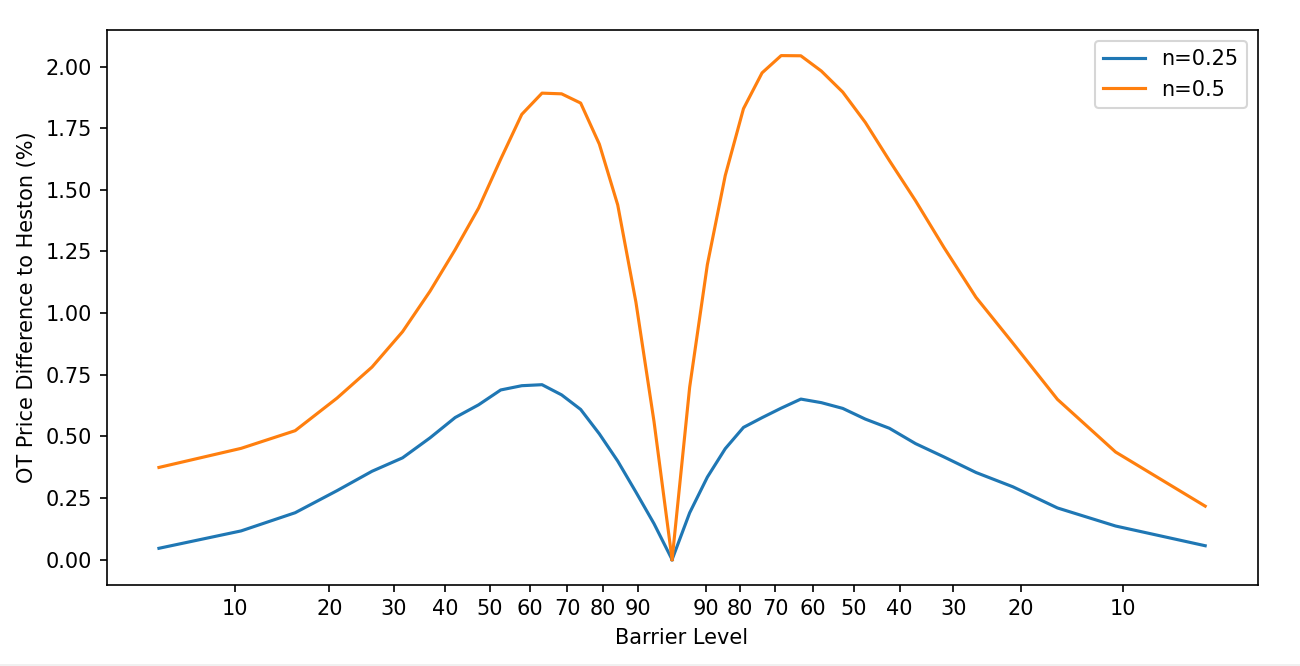
Результаты моделирования показали, что использование модели Double Heston приводит к увеличению цен на опционы типа one-touch и knockout, находящиеся вне денег (out-of-the-money), на величину, сопоставимую или превышающую спред между ценой покупки и продажи (bid/ask spread). Данный эффект демонстрирует преимущества включения стохастической корреляции между ценой базового актива и его волатильностью. В частности, корректное моделирование этой зависимости позволяет более точно оценивать стоимость опционов, чувствительных к экстремальным изменениям цены базового актива, что особенно важно для опционов с барьером и опционов, основанных на достижении определенного ценового уровня.

Разница в ценах при однократном касании для модели Хестона варьируется в зависимости от уровня барьера.

Влияние и Перспективы Развития

Усовершенствованные модели волатильности позволяют значительно повысить точность оценки стоимости экзотических опционов, таких как барьерные опционы и свопы на волатильность. Традиционные методы часто не учитывают динамику волатильности, что приводит к неверной оценке рисков и возможностей. Новые подходы, учитывающие стохастическую природу волатильности и её связь с движением спотовой цены, позволяют более адекватно отразить реальную рыночную стоимость этих сложных финансовых инструментов. Это особенно важно для трейдеров и институциональных инвесторов, использующих экзотические опционы для хеджирования рисков или получения прибыли от прогнозирования изменений волатильности. Более точная оценка стоимости также способствует повышению эффективности рынка и снижению транзакционных издержек.

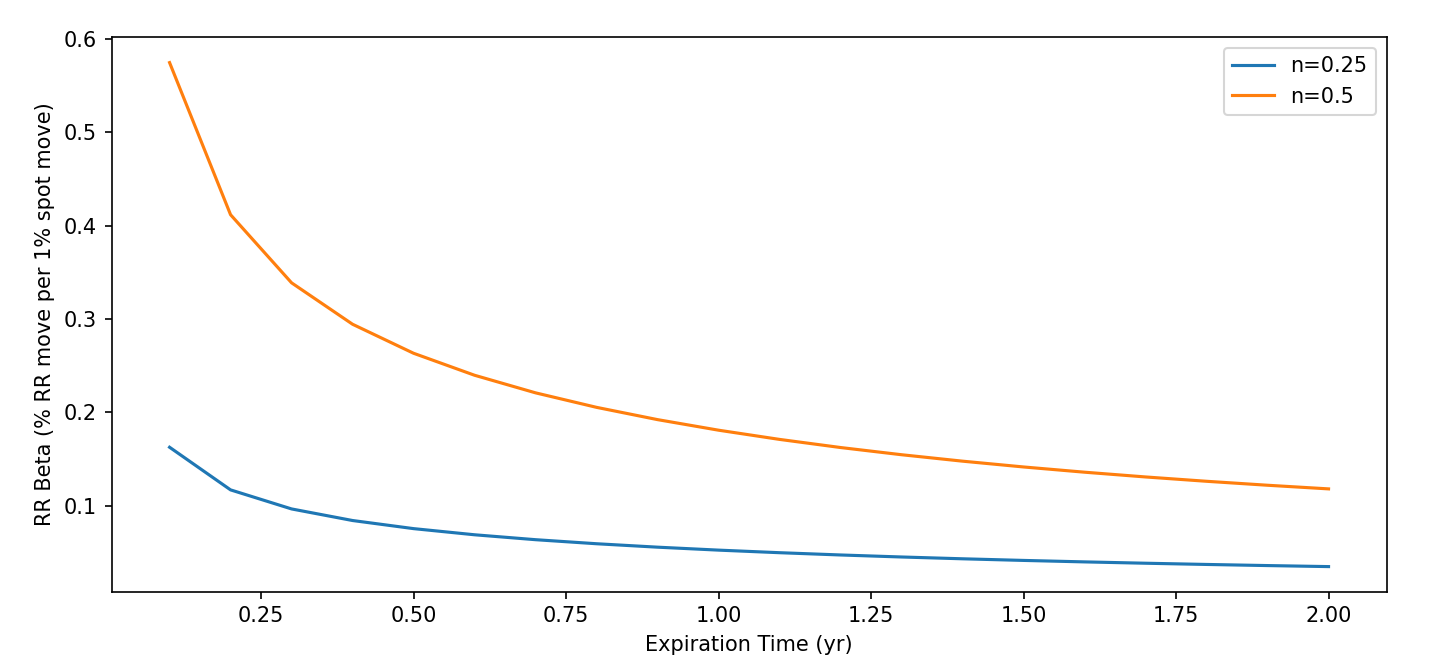
Углубленное понимание бета-коэффициента риск-реверса — взаимосвязи между изменениями уклона волатильности и движениями спотовой цены — открывает новые возможности для разработки более эффективных торговых стратегий. Исследования показывают, что точное определение этой корреляции позволяет трейдерам более адекватно оценивать риски и потенциальную прибыль при торговле опционами. В частности, знание бета-коэффициента позволяет прогнозировать, как изменения в ожиданиях рынка повлияют на цены опционов с различными страйками, что особенно важно для торговли экзотическими опционами и волатильностными свопами. Это, в свою очередь, дает возможность создавать более сложные и прибыльные стратегии, основанные на предсказании динамики уклона волатильности в зависимости от движения базового актива, и, следовательно, повышает эффективность управления рисками на финансовых рынках.

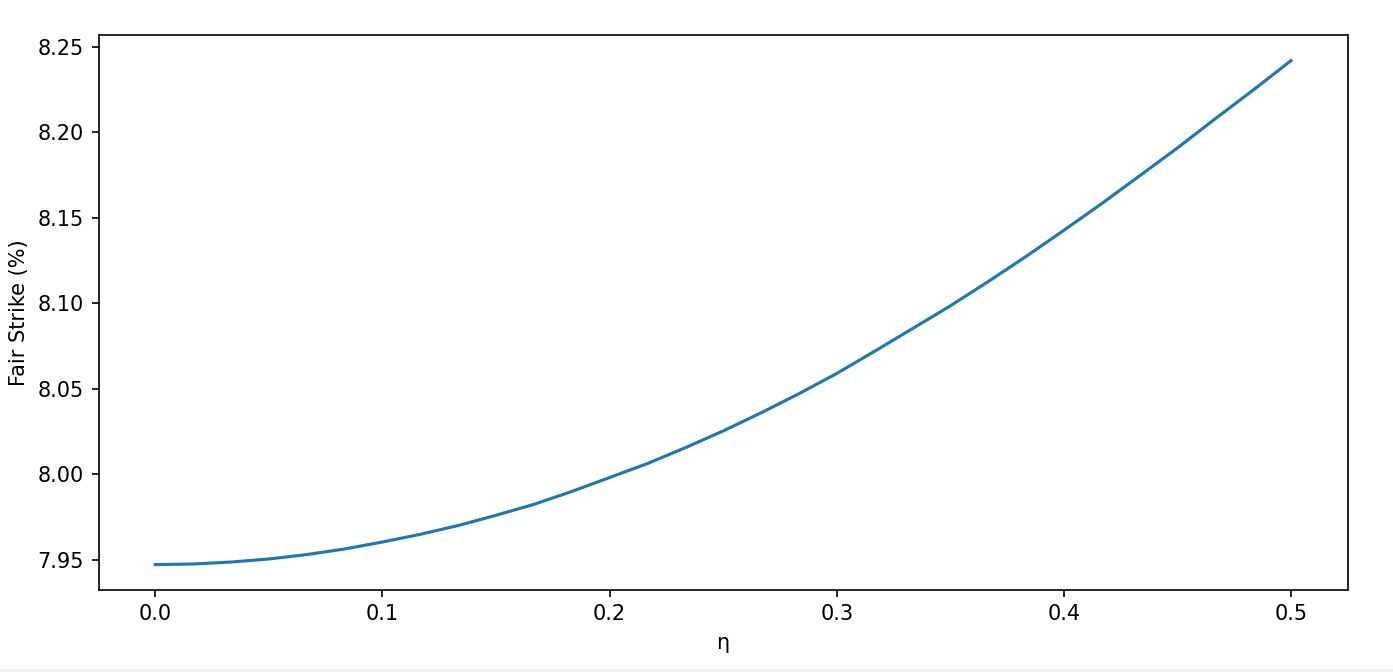
Включение стохастической корреляции между ценой базового актива и его волатильностью оказывает заметное влияние на ценообразование производных финансовых инструментов. Исследования показывают, что учет этой взаимосвязи приводит к увеличению справедливой цены свопов на волатильность, что может существенно повлиять на стратегии хеджирования и управления рисками. Более того, наблюдается рост цен на опционы с барьером и опционы с выбытием, причем эти изменения зачастую сопоставимы или даже превышают величину спреда между ценой покупки и продажи, что подчеркивает практическую значимость данной модели для трейдеров и финансовых институтов. Это указывает на необходимость дальнейшей разработки и внедрения моделей, учитывающих стохастическую корреляцию, для повышения точности оценки и эффективности управления рисками на финансовых рынках.

График демонстрирует зависимость справедливой страйки волатильности свопа от волатильности корреляции.

Исследование демонстрирует, что даже в сложных моделях, таких как расширенная модель Хестона со стохастической корреляцией между ценой актива и волатильностью, игнорирование динамики этой корреляции приводит к неточностям в ценообразовании экзотических опционов и свопов волатильности. Это подтверждает, что человеческое восприятие взаимосвязей, как и математическое моделирование, склонно к упрощениям. Как заметил Джон Локк: «Ум — это пустая шкатулка». В данном контексте, это означает, что даже самые изощренные модели нуждаются в постоянном дополнении и уточнении, чтобы отразить реальную сложность экономических процессов. Недостаточно просто учитывать волатильность; необходимо понимать, как она связана с движением цены актива, иначе модель останется неполной.

Куда Ведут Эти Связи?

Представленная работа, расширяющая модель Хесто за счёт стохастической корреляции между ценой актива и волатильностью, лишь подтверждает старую истину: каждая гипотеза — это попытка убедить себя, что мир предсказуем. Улучшение точности при оценке барьерных опционов и волатильности свопов — это, безусловно, полезно, но это лишь локальное снижение неопределённости в океане хаоса. Остается вопрос: действительно ли более точная оценка производных инструментов приближает нас к пониманию фундаментальных движущих сил рынка, или это просто более изящный способ игнорировать сложность?

Дальнейшие исследования неизбежно потребуют рассмотрения нелинейных зависимостей между корреляцией и другими параметрами модели. Возможно, стоит пересмотреть саму концепцию «корреляции» как статичной величины, заменив её на более гибкую метрику, отражающую динамические изменения в восприятии риска. Инфляция — это просто коллективное беспокойство о будущем, и корреляция, вероятно, является его отражением в графиках.

В конечном счёте, задача состоит не в создании идеальной модели, а в осознании её ограниченности. Человек — не рациональный агент, а биологическая гипотеза с систематическими ошибками, и любые попытки предсказать его поведение обречены на частичный провал. Именно в этом несовершенстве и заключается истинная красота — и вызов — финансового моделирования.

Оригинал статьи: https://arxiv.org/pdf/2602.01376.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-04 03:20