Городской транспорт: баланс эффективности и справедливости

Автор: Денис Аветисян

Новое исследование анализирует сложности оптимизации общественного транспорта с учетом как общей эффективности, так и социальной справедливости распределения ресурсов.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

На рисунке продемонстрирована задача оптимального прохождения маршрута, где решение [latex] S_1 = \{1, 5\} [/latex] с соответствующей стоимостью проезда указывает на выбор наиболее эффективного пути среди возможных автобусных остановок и пешеходных участков. — На рисунке продемонстрирована задача оптимального прохождения маршрута, где решение $S_1 = \{1, 5\}$ с соответствующей стоимостью проезда указывает на выбор наиболее эффективного пути среди возможных автобусных остановок и пешеходных участков.

Анализ вычислительной сложности и разработка приближенных алгоритмов для оптимизации транспортных сетей с учетом различных критериев благосостояния.

Несмотря на значительные успехи в оптимизации транспортных сетей, обеспечение справедливого распределения ресурсов и эффективности часто представляется взаимоисключающими задачами. В работе ‘Efficient Investment in Multi-Agent Models of Public Transportation’ исследуется сложность оптимизации инвестиций в общественный транспорт с учетом как утилитарного благосостояния (эффективности), так и эгалитарного (справедливости). Показано, что задача достижения приблизимально оптимальных решений для эгалитарного благосостояния является NP-полной даже в простых линейных топологиях, в то время как для утилитарного благосостояния удается найти полиномиальные алгоритмы. Какие новые подходы к алгоритмической разработке позволят преодолеть эти ограничения и создать более справедливые и эффективные транспортные системы?

Сложность городского движения: вызов современному планированию

Современные города не могут функционировать без развитых систем общественного транспорта, однако оптимизация этих сетей представляет собой сложную задачу. Эффективное планирование маршрутов и расписаний сталкивается с непредсказуемостью пассажиропотока, ограничениями инфраструктуры и необходимостью учитывать разнообразные потребности жителей. Простое увеличение количества транспортных средств не всегда приводит к улучшению ситуации, поскольку может усугубить дорожные заторы и негативно повлиять на экологию. Сложность заключается в том, что городская мобильность — это динамичная система, подверженная влиянию множества факторов, включая время суток, погодные условия, события и даже настроение горожан. Поэтому, поиск оптимальных решений требует комплексного подхода, учитывающего все эти переменные и направленного на повышение доступности, скорости и удобства общественного транспорта для всех категорий населения.

Традиционные методы планирования и оптимизации транспортных систем зачастую оказываются неэффективными перед лицом реальной сложности городской среды. Непредсказуемость пассажиропотока, обусловленная различными факторами — от времени суток и погодных условий до спонтанных событий и индивидуальных предпочтений — создает значительные трудности для построения устойчивых и гибких маршрутов. Кроме того, существующая инфраструктура, сформированная исторически и ограниченная физическими и финансовыми ресурсами, не всегда позволяет эффективно реагировать на меняющиеся потребности населения. Моделирование, основанное на упрощенных предположениях о равномерности распределения пассажиров или игнорировании влияния пробок, приводит к неточным прогнозам и, как следствие, к неоптимальному использованию транспортных средств и увеличению времени ожидания для пассажиров. Поэтому, для создания действительно эффективной системы общественного транспорта необходим переход к более сложным и адаптивным методам планирования, учитывающим динамику городской жизни и особенности конкретной инфраструктуры.

Оптимизация транспортных сетей в современных городах требует не просто удовлетворения текущего спроса, но и максимизации общей пользы для общества, что часто измеряется с помощью концепции утилитарного благосостояния. Это означает, что при проектировании маршрутов и расписаний необходимо учитывать не только количество перевезенных пассажиров, но и совокупную выгоду, которую каждый маршрут приносит всем пользователям системы. \text{Общая польза} = \sum_{i=1}^{n} U(x_i) , где U(x_i) — функция полезности для i-го пользователя, а x_i — доступность и качество транспортного обслуживания. Такой подход требует сложного анализа, учитывающего различные факторы, такие как время в пути, стоимость проезда, перегруженность транспорта и доступность для различных групп населения. Эффективное проектирование, основанное на максимизации утилитарного благосостояния, позволяет создать транспортную систему, которая не только справляется с текущими потребностями, но и способствует повышению качества жизни всех горожан.

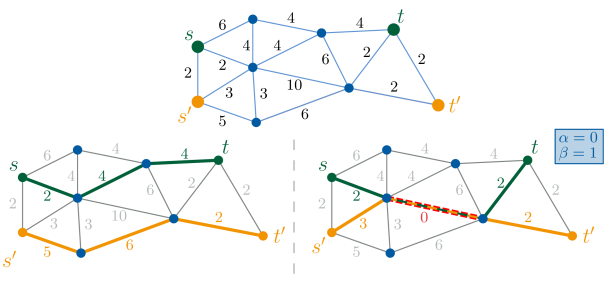
Изменение стоимости ребра в графе (обозначено пунктиром) приводит к перестройке кратчайших путей, используемых агентами для перемещения по сети.

Математическое моделирование транспортных потоков: NTP и PTP

Проблема сетевого транзита (Network Transit Problem, NTP) представляет собой математическую модель, используемую для оптимизации инвестиций в развитие транспортной сети, в частности, в улучшение связей между узлами (например, дорогами или линиями общественного транспорта). Основная цель NTP — минимизация общего времени в пути для всех пользователей сети путём определения оптимального набора улучшений, таких как строительство новых дорог, увеличение пропускной способности существующих, или внедрение приоритетных полос для общественного транспорта. Модель учитывает как стоимость улучшений, так и снижение времени в пути, позволяя оценить экономическую эффективность различных сценариев развития транспортной инфраструктуры. T = \sum_{i \in V} \sum_{j \in V} t_{ij}x_{ij}[/latex], где T — общее время в пути, t_{ij}[/latex] — время в пути между узлами i и j, а x_{ij}[/latex> — переменная, определяющая наличие и пропускную способность связи между этими узлами.

Проблема транзита по пути (PTP) является специализированной задачей, фокусирующейся на оптимизации размещения автобусных остановок. В рамках PTP, транспортная сеть, как правило, моделируется с использованием линейных графов, где узлы представляют собой потенциальные местоположения остановок, а ребра — участки маршрута между ними. Оптимизация в данном контексте направлена на минимизацию общего времени в пути для пассажиров, учитывая стоимость размещения остановок и расстояние между ними. Эффективное решение PTP позволяет определить оптимальное количество и расположение остановок для заданного маршрута, что напрямую влияет на удобство и скорость транспортного сообщения.

Модели сетевого транзита (NTP) и частный случай, проблема транзита по пути (PTP), несмотря на свою эффективность в оптимизации транспортных сетей, сталкиваются с серьезными вычислительными сложностями. Это связано с тем, что оба типа задач относятся к классу NP-трудных, что означает, что время, необходимое для нахождения оптимального решения, экспоненциально возрастает с увеличением размера сети (количества ребер и узлов). Даже для умеренно крупных транспортных систем, точное решение NTP или PTP может потребовать неприемлемо больших вычислительных ресурсов и времени, что вынуждает исследователей и практиков прибегать к эвристическим алгоритмам и приближенным методам для получения приемлемых решений в разумные сроки.

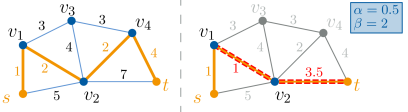
Сравнительный анализ методов RDP и NTP показывает, что при одинаковом бюджете на изменение одной связи, NTP (пунктирные линии) минимизирует затраты, в то время как RDP, с масштабированием весов связей на [latex]\zeta = 2[/latex], обеспечивает альтернативное решение. — Сравнительный анализ методов RDP и NTP показывает, что при одинаковом бюджете на изменение одной связи, NTP (пунктирные линии) минимизирует затраты, в то время как RDP, с масштабированием весов связей на \zeta = 2, обеспечивает альтернативное решение.

Преодоление вычислительной сложности: алгоритмы и приближения

Как задачи определения оптимального маршрута в транспортной сети (NTP) и задача планирования общественного транспорта (PTP), так и NTP, и PTP относятся к классу NP-полных задач. Это означает, что не существует известного алгоритма, способного найти точное оптимальное решение за полиномиальное время относительно размера входных данных. По мере увеличения количества вершин (узлов) и ребер (связей) в сети, время, необходимое для нахождения точного решения, экспоненциально возрастает, что делает практическое применение точных алгоритмов невозможным для крупных сетей. Следовательно, для решения NTP и PTP в реальных условиях часто используются приближенные алгоритмы и эвристики, которые находят решения, близкие к оптимальным, за приемлемое время.

Алгоритм Дейкстры является базовым методом поиска кратчайших путей в графе и играет ключевую роль в оценке производительности транспортных сетей. Он позволяет определить минимальное расстояние или время в пути между двумя узлами, учитывая веса ребер, представляющие собой, например, длину маршрута или время прохождения. В контексте транспортных сетей, алгоритм используется для вычисления оптимальных маршрутов, анализа доступности различных пунктов назначения и оценки общей эффективности сети с точки зрения времени в пути или стоимости проезда. Реализация алгоритма Дейкстры предполагает итеративное построение дерева кратчайших путей от начальной точки до всех остальных узлов графа, используя жадный подход и гарантируя нахождение оптимального решения при неотрицательных весах ребер.

В связи с тем, что задачи NTP и PTP являются NP-полными, поиск точных оптимальных решений для крупных сетей требует неприемлемых вычислительных затрат. Поэтому широко используются приближенные алгоритмы, позволяющие находить решения, близкие к оптимальным, за разумное время. При этом, математически доказано, что для задачи максимизации эгалитарного благосостояния (egalitarian welfare) невозможно получить приближение с точностью лучше, чем (α+1)/(2α)[/latex>, где α — параметр, определяющий компромисс между справедливостью и эффективностью. Данное ограничение является фундаментальным свойством задачи и влияет на выбор и оценку алгоритмов приближенного решения.

Существует полиномиальный алгоритм для решения задачи сетевого транзита для одного агента, сложность которого составляет O(\beta m^2 log m)[/latex>, где \beta представляет бюджет, а m — количество вершин в сети. Данный алгоритм обеспечивает решение задачи за время, полиномиально зависящее от размера входных данных, что делает его практически применимым для сетей умеренного размера. Эффективность алгоритма обусловлена использованием специализированных структур данных и техник оптимизации, позволяющих снизить вычислительную сложность по сравнению с подходами, основанными на полном переборе вариантов.

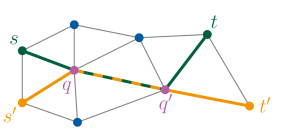
На схеме показана структура 22-NTP, характеризующаяся наличием общих участков на кратчайших путях агентов.

Влияние на развитие умных городов

Эффективная оптимизация сетей общественного транспорта, даже с использованием приближенных алгоритмов, оказывает существенное влияние на мобильность и доступность городской среды. Исследования показывают, что незначительные упрощения в расчетах не приводят к критической потере качества решения, но позволяют значительно ускорить процесс планирования маршрутов и расписаний. Это, в свою очередь, способствует снижению времени в пути для пассажиров, повышению пропускной способности транспортной системы и улучшению связности различных районов города. В результате, жители получают более удобный и эффективный доступ к рабочим местам, образованию, здравоохранению и другим важным сервисам, что положительно сказывается на качестве жизни и экономическом развитии города.

Сокращение времени в пути и повышение эффективности транспортных сетей оказывают существенное влияние на экономическую жизнеспособность городов и состояние окружающей среды. Более быстрое перемещение людей и товаров способствует повышению производительности труда, снижает транспортные издержки и открывает новые возможности для бизнеса. Параллельно, оптимизация транспортных потоков приводит к уменьшению выбросов вредных веществ в атмосферу, снижению потребления топлива и улучшению качества воздуха, что напрямую способствует более устойчивому развитию городской среды. Экономический эффект проявляется не только в прямых выгодах для бизнеса и жителей, но и в снижении затрат на инфраструктуру благодаря более рациональному использованию существующих ресурсов, а также в повышении привлекательности города для инвестиций и туризма.

Дальнейшие исследования в области продвинутых приближенных алгоритмов и эффективных методов обхода графов представляются критически важными для создания более разумных и устойчивых городов. Установлено, что для достижения максимального общественного благосостояния, даже незначительные гарантии приближения (α^{-1}) вполне достижимы без использования излишне сложных алгоритмов. Это открывает возможности для разработки практичных и масштабируемых решений, способных оптимизировать транспортные сети, снизить время в пути и, как следствие, улучшить экономические показатели и экологическую обстановку в городских агломерациях. Акцент на простоту и эффективность алгоритмов позволит быстрее внедрять инновации в системы городского планирования и управления, делая города более комфортными и удобными для жизни.

Сравнение кратчайших путей без (слева) и с оптимальными (справа) инвестициями демонстрирует эффективность предложенного алгоритма.

Исследование, представленное в данной работе, демонстрирует фундаментальную сложность оптимизации транспортных систем с учетом принципов справедливости. Поиск решений, максимизирующих благосостояние всех участников, оказывается вычислительно непосильной задачей, значительно превосходящей по сложности оптимизацию, ориентированную лишь на эффективность. Как некогда заметил Г.Х. Харди: «Математика — это наука о том, что можно логически заключить, а не о том, что можно эмпирически обнаружить». Эта фраза особенно уместна здесь, поскольку работа выявляет границы возможностей алгоритмического приближения к идеалу справедливого распределения ресурсов в транспортной сети, подчеркивая, что даже в сфере оптимизации существуют неразрешимые проблемы, определяемые не практическими ограничениями, а фундаментальной сложностью самой задачи.

Куда же дальше?

Работа выявила, как и следовало ожидать, что стремление к справедливости в организации общественного транспорта обходится значительно дороже, чем простое повышение эффективности. Это не открытие, но констатация того, что сложность не всегда оправдана. Попытки «оптимизировать» равенство, используя приближенные алгоритмы, наталкиваются на принципиальные ограничения, которые не позволяют достичь приемлемых результатов без значительных вычислительных затрат. Следует задаться вопросом: не проще ли признать, что абсолютная справедливость — это иллюзия, а погоня за ней — лишь усложнение системы?

Будущие исследования должны сосредоточиться не на создании всё более изощренных алгоритмов, а на разработке простых, понятных критериев оценки справедливости. Возможно, стоит пересмотреть саму постановку задачи, отказавшись от стремления к глобальной оптимизации в пользу локальных, более реалистичных решений. И, что важнее, следует признать: иногда лучшее решение — это отсутствие решения, когда его поиск приводит к неоправданному усложнению системы.

Очевидно, что алгоритм Дейкстры, несмотря на свою элегантность, не является панацеей. Он лишь инструмент, а не цель. Задача состоит не в том, чтобы «выжать» максимум из этого инструмента, а в том, чтобы понять, когда его использование оправдано, а когда необходимо искать более простые и эффективные решения. И, возможно, самое важное: помнить, что ясность важнее сложности.

Оригинал статьи: https://arxiv.org/pdf/2602.03687.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-04 11:45