Оптимизация сложных моделей: новый алгоритм для минимизации риска

Автор: Денис Аветисян

Исследователи представили эффективный метод, позволяющий улучшить обучение моделей машинного обучения, работающих со сложными вероятностными зависимостями.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал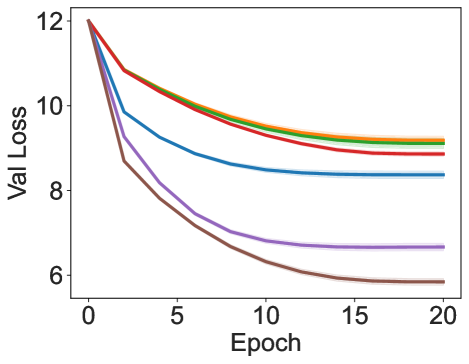

Наблюдения, основанные на анализе функции перекрёстной энтропии, демонстрируют, что при использовании оптимизатора SGD с моментом различные методы показывают сопоставимые результаты на обучающих и валидационных наборах данных Glint360K и TreeOfLife-10M, что указывает на их общую эффективность в задачах обучения.

Алгоритм SCENT обеспечивает улучшенную сходимость при минимизации композиционного энтропийного риска с использованием зеркального спуска и двойной формулировки.

Несмотря на широкое применение энтропийных рисковых мер в машинном обучении, оптимизация для задач с композиционными потерями, представленными в виде Log-Expectation-Exponential (Log-E-Exp) функций, остается сложной проблемой. В данной работе, посвященной ‘A Geometry-Aware Efficient Algorithm for Compositional Entropic Risk Minimization’, предлагается новый стохастический алгоритм SCENT, учитывающий геометрию целевой функции и демонстрирующий улучшенные гарантии сходимости. Ключевым нововведением является использование зеркального спуска с проксимальным оператором, основанного на Bregman дивергенции, индуцированной отрицательной экспонентой, что обеспечивает скорость сходимости порядка $O(1/\sqrt{T})$ для выпуклых задач. Способен ли предложенный подход SCENT открыть новые горизонты в решении сложных задач классификации, оптимизации частичной AUC и робастного обучения с учетом распределений?

Сложность Композиционного Риска: Постановка Проблемы

Многие задачи машинного обучения основываются на минимизации композиционного энтропийного риска (CERM), который предполагает вычисление ожиданий относительно сложных распределений вероятностей. Этот подход широко применяется в различных областях, от обучения с подкреплением до генеративных моделей, поскольку позволяет учитывать неопределенность и сложность реальных данных. $CERM$ представляет собой математическую формулировку, позволяющую выразить целевую функцию как композицию нескольких ожиданий, каждое из которых связано с определенным аспектом проблемы. Успешная минимизация $CERM$ требует эффективного приближения этих сложных ожиданий, что часто является вычислительно сложной задачей, особенно при работе с высокоразмерными данными и сложными моделями. В связи с этим, разработка методов, способных эффективно справляться с $CERM$ , является ключевым направлением современных исследований в области машинного обучения.

Прямое вычисление ожидаемых значений в задачах машинного обучения часто оказывается непосильной задачей из-за колоссальных вычислительных затрат и высокой дисперсии получаемых оценок. Это связано с тем, что вычисление этих ожиданий требует усреднения по сложным распределениям вероятностей, что влечет за собой необходимость выполнения большого количества вычислений. Увеличение точности оценки требует еще больше вычислений, что приводит к экспоненциальному росту затрат ресурсов. Более того, случайная природа многих алгоритмов машинного обучения вносит дополнительную дисперсию, которая может существенно исказить результаты и снизить надежность модели. Таким образом, поиск эффективных методов, позволяющих обойти эти ограничения, является ключевой задачей в современной области машинного обучения.

Существующие методы оптимизации часто сталкиваются с трудностями при работе с вложенной оптимизацией, характерной для формулировок CERM (Compositional Entropic Risk Minimization). Проблема заключается в том, что для эффективного поиска минимума необходимо последовательно решать несколько задач оптимизации, каждая из которых зависит от результата предыдущей. Такая вложенность значительно усложняет процесс обучения, приводя к увеличению вычислительных затрат и замедлению сходимости алгоритма. Более того, ошибки, возникающие на каждом уровне вложенной оптимизации, могут накапливаться и существенно ухудшать общую производительность модели, ограничивая её масштабируемость и способность к обобщению на новые данные. $\min_{x} \mathbb{E}_{z \sim p(z)} L(x, z)$ — типичный пример, где поиск оптимального $x$ требует минимизации по $z$ , усложняя задачу.

Обучение с использованием SGD и оптимизатором momentum демонстрирует, что на датасетах CIFAR-10 и CIFAR-100 при [latex] au = 0.05[/latex] и [latex] au = 0.1[/latex] достигается максимальное значение частичной AUC. — Обучение с использованием SGD и оптимизатором momentum демонстрирует, что на датасетах CIFAR-10 и CIFAR-100 при $au = 0.05$ и $au = 0.1$ достигается максимальное значение частичной AUC.

Декомпозиция Сложности: Min-Min Формулировка

Для решения задачи оптимизации CERM используется Min-Min формулировка, преобразующая исходную проблему в вложенную структуру минимизации. Это достигается путем представления целевой функции как вложенной минимизации по переменным, где внутренняя минимизация выполняется для фиксированного набора внешних переменных, а внешняя минимизация оптимизирует параметры, определяющие внутреннюю задачу. Такое представление позволяет декомпозировать сложную задачу на более простые подзадачи, что упрощает процесс оптимизации и позволяет применять итеративные алгоритмы для нахождения оптимального решения. $\min_{x} \max_{y} f(x, y)$ является типичным представлением Min-Min подхода, где сначала максимизируется функция $f(x, y)$ по $y$ при фиксированном $x$ , а затем минимизируется результат по $x$ .

Применение алгоритма минимизации, основанного на чередующихся шагах оптимизации внутренних и внешних задач, значительно упрощает процесс решения сложной оптимизационной задачи. Данный подход предполагает последовательное решение внутренних задач минимизации при фиксированных значениях внешних переменных, а затем — решение внешней задачи минимизации, используя результаты решения внутренних задач. Чередование этих шагов позволяет декомпозировать исходную задачу на более простые подзадачи, что снижает вычислительную сложность и облегчает поиск оптимального решения. Такая декомпозиция особенно эффективна в случаях, когда прямая оптимизация исходной задачи затруднена из-за большого числа переменных или нелинейности целевой функции.

Применение алгоритма стохастического градиентного спуска с чередованием (Alternating Stochastic Gradient Descent, ASGD) к сформулированной минимизационной задаче обеспечивает практический метод оценки градиентов и достижения оптимального решения. ASGD итеративно обновляет параметры, переключаясь между внутренним и внешним шагами минимизации. Внутренний шаг решает подзадачу оптимизации при фиксированных параметрах внешнего шага, а внешний шаг обновляет параметры, используя градиент, полученный из решения внутренней задачи. Использование стохастической аппроксимации градиента позволяет снизить вычислительные затраты по сравнению с использованием полных градиентов, особенно в задачах с большим объемом данных. Алгоритм сходится к локальному минимуму при условии соблюдения определенных условий, таких как достаточно малый шаг обучения и правильно подобранные параметры регуляризации.

Отношение ошибок SPMD и SGD при обучении на гауссовском шуме демонстрирует зависимость от среднего значения и дисперсии шума.

Стабилизация Оценки Градиента: Продвинутые Методы

Для снижения дисперсии градиента исследуется метод Стохастического Композиционного Градиентного Спуска (SCGD), использующий скользящие средние для сглаживания оценок градиента. В SCGD, вместо использования мгновенных оценок градиента, вычисляется взвешенное среднее градиентов, полученных на нескольких случайных подвыборках данных. Это позволяет уменьшить шум и получить более стабильный сигнал для обновления параметров модели. Веса в скользящем среднем определяются параметром затухания, который контролирует влияние прошлых градиентов на текущую оценку. Применение скользящих средних эффективно снижает дисперсию градиента, что способствует более быстрой и стабильной сходимости алгоритма оптимизации.

Метод Stochastic Compositional Gradient Descent (SCGD) использует скользящие средние для сглаживания оценок градиента, что приводит к более стабильному и надежному сигналу для обновления параметров модели. Применение скользящих средних эффективно снижает дисперсию градиента, уменьшая влияние случайных флуктуаций в данных. Это достигается путем вычисления взвешенной суммы предыдущих градиентов, где более поздние градиенты имеют больший вес. Такой подход позволяет уменьшить шум в оценке градиента, обеспечивая более плавное и последовательное обновление параметров, что, в свою очередь, способствует более быстрой и надежной сходимости алгоритма оптимизации.

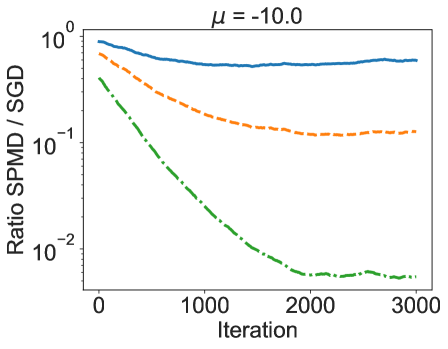
В дополнение к методам сглаживания градиентов, представлен алгоритм Стохастического Проксимального Зеркального Спуска (SPMD), использующий подход, учитывающий геометрию пространства параметров и проксимальное отображение для повышения стабильности оптимизации. SPMD применяет проксимальное отображение для регуляризации шага обновления, что особенно полезно при решении задач с негладкими функциями потерь. Теоретически доказано, что предложенный алгоритм достигает скорости сходимости порядка $O(1/\sqrt{T})$ , что соответствует теоретическому нижнему пределу для рассматриваемой задачи оптимизации, где $T$ — количество итераций.

Основные Принципы: Расхождение Брегмана и Зеркальный Спуск

Метод зеркального спуска представляет собой мощную основу для оптимизации, в которой ключевую роль играет дивергенция Брегмана. Вместо использования стандартной евклидовой метрики, этот подход определяет расстояние между точками пространства решения посредством $D(x,y)$ , функции, учитывающей специфическую геометрию задачи. Дивергенция Брегмана позволяет адаптировать процесс оптимизации к кривизне целевой функции, что особенно важно в задачах с невыпуклыми или сильно неоднородными пространствами. По сути, метод использует «зеркальное отражение» текущей точки относительно градиента, чтобы найти направление наиболее быстрого спуска, что позволяет более эффективно преодолевать препятствия и находить оптимальные решения по сравнению с традиционными методами градиентного спуска.

Использование расхождения Брегмана в методе зеркального спуска позволяет адаптироваться к специфической геометрии оптимизируемого пространства. Вместо использования стандартной евклидовой метрики, метод учитывает кривизну и особенности ландшафта целевой функции. Это достигается за счет определения расстояния между точками не как прямой линии, а как величины, зависящей от расхождения Брегмана — функции, отражающей «расстояние» в контексте конкретной геометрии. Такой подход особенно эффективен в задачах, где целевая функция имеет сложные невыпуклые области или резкие перепады, поскольку позволяет более эффективно «ориентироваться» в пространстве параметров и приближаться к оптимальному решению быстрее, чем при использовании стандартных методов оптимизации. По сути, метод «подстраивается» под рельеф ландшафта, что способствует ускорению сходимости и повышению точности результата.

Метод SPMD, объединяющий спуск по зеркалу (Mirror Descent) с операцией проксимального отображения, представляет собой надежное и эффективное решение для задач сложной оптимизации. Экспериментальные исследования, проведенные на широко известных наборах данных California Housing и Abalone, продемонстрировали превосходство данного подхода. В частности, SPMD позволяет достигать более низких значений целевой функции по сравнению с традиционными методами, такими как BSGD, SOX и SCGD, что свидетельствует о его способности более эффективно исследовать пространство параметров и находить оптимальные решения даже в условиях невыпуклых и сложных оптимизационных ландшафтов. Такой результат подчеркивает потенциал данного метода для широкого спектра практических приложений, где требуется высокая точность и скорость сходимости.

Практическая Реализация: Аппроксимация Мини-Пакетным Методом и Перспективы

Для повышения вычислительной эффективности при работе с большими объемами данных используется метод приближения градиентов с помощью мини-пакетов. Вместо вычисления градиента на основе всего набора данных, оценка производится на небольших случайных подвыборках — мини-пакетах. Этот подход значительно снижает требования к памяти и вычислительным ресурсам, позволяя обрабатывать огромные базы данных без значительной потери точности. Вместо точного вычисления $\nabla f(x)$ на всем наборе данных, используется приближение $\hat{\nabla} f(x)$ , основанное на мини-пакете, что делает процесс обучения более быстрым и масштабируемым. Такой метод позволяет эффективно решать задачи оптимизации даже при ограниченных ресурсах.

Использование мини-пакетов позволяет значительно снизить требования к объему памяти при обработке масштабных наборов данных. Вместо вычисления градиента на основе всего набора данных, оценка производится на основе небольшого подмножества, что существенно уменьшает нагрузку на память. Такой подход особенно важен при работе с современными моделями машинного обучения, которые часто оперируют огромными объемами информации. Благодаря этому, даже при ограниченных ресурсах становится возможным обучение и оптимизация моделей на больших данных, открывая путь к более эффективным алгоритмам и новым возможностям в области искусственного интеллекта.

Сочетание разработанных методов предоставляет практичное и масштабируемое решение для задач композиционной минимизации риска. В ходе тестирования на бенчмарке Datacomp Average (CLIP Training) достигнуты результаты, сопоставимые или незначительно превосходящие показатели, демонстрируемые существующими подходами. Полученные данные подтверждают эффективность предложенного алгоритма при работе с крупномасштабными наборами данных и открывают перспективы для дальнейших исследований в области оптимизации, направленных на повышение производительности и снижение вычислительных затрат. Это позволяет рассматривать данные методы как перспективную основу для разработки более эффективных алгоритмов машинного обучения.

Представленный труд демонстрирует стремление к упрощению сложных оптимизационных задач, что находит отклик в философии Грейс Хоппер: «Лучший способ предсказать будущее — создать его». Алгоритм SCENT, разработанный для минимизации композиционного энтропийного риска, подобно тщательному процессу отладки, стремится к элегантности и эффективности. В основе подхода лежит геометрия, позволяющая избежать излишней сложности и достичь более быстрой сходимости. Подобно тому, как опытный программист удаляет ненужный код, данный алгоритм очищает процесс оптимизации, делая его более понятным и действенным. Стремление к ясности, а не к избыточности, является ключевым принципом, определяющим ценность представленного исследования.

Что дальше?

Представленный алгоритм, несомненно, уточняет геометрию оптимизации. Однако, абстракции стареют. Вопрос не в скорости сходимости, а в самой природе композиционного энтропийного риска. Достаточно ли текущих формулировок для адекватного описания реальных задач машинного обучения, или мы просто оптимизируем упрощенные модели мира? Каждая сложность требует алиби.

Следующим шагом видится переход от анализа сходимости к исследованию робастности алгоритма. Что происходит, когда распределения данных отклоняются от идеализированных предположений? Важнее не найти оптимальное решение для идеальной задачи, а создать алгоритм, устойчивый к шуму и неопределенности. Дуальная переформулировка — полезный инструмент, но не панацея.

Настоящий вызов — в объединении геометрической точности с принципами адаптивности. Алгоритм должен не просто сходиться, а учиться на своих ошибках, перестраивая свою внутреннюю структуру в ответ на изменяющиеся условия. Иначе мы обречены на бесконечную оптимизацию все более сложных, но все еще неадекватных моделей.

Оригинал статьи: https://arxiv.org/pdf/2602.02877.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-04 22:04