Обратное моделирование: новый подход к решению сложных задач

от

Автор: Денис Аветисян

В статье представлен эффективный байесовский фреймворк, сочетающий суррогатное моделирование и байесовское обратное моделирование для повышения точности и скорости решения обратных задач.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал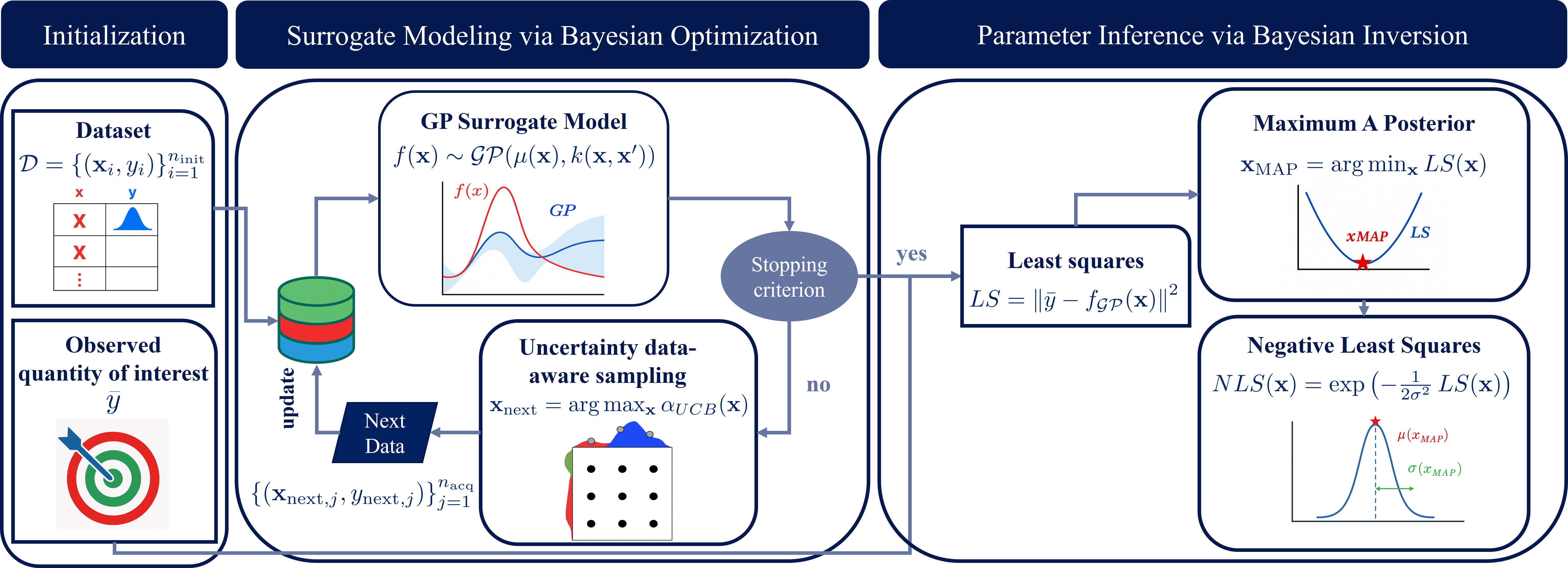
Предлагаемая байесовская структура для решения обратных задач объединяет оптимизацию на основе байесовской оптимизации (BO) и байесовский вывод (BI), где итеративное уточнение суррогатной GP-модели посредством BO, управляемое стратегией UCB, позволяет, достигнув сходимости, выполнить параметрическую инференцию посредством минимизации методом наименьших квадратов (LS) и получить оценку максимальной апостериорной вероятности (MAP) и апостериорное распределение с использованием формулировки отрицательных наименьших квадратов (NLS).
Предлагаемая байесовская структура для решения обратных задач объединяет оптимизацию на основе байесовской оптимизации (BO) и байесовский вывод (BI), где итеративное уточнение суррогатной GP-модели посредством BO, управляемое стратегией UCB, позволяет, достигнув сходимости, выполнить параметрическую инференцию посредством минимизации методом наименьших квадратов (LS) и получить оценку максимальной апостериорной вероятности (MAP) и апостериорное распределение с использованием формулировки отрицательных наименьших квадратов (NLS).

Объединение гауссовских процессов и байесовского вывода для эффективного определения параметров и оценки неопределенности в задачах с ограниченными данными и вычислительно сложными моделями.

Обратные задачи часто сталкиваются с ограничениями, связанными с вычислительной сложностью и дефицитом данных. В настоящей работе, озаглавленной ‘An Efficient Bayesian Framework for Inverse Problems via Optimization and Inversion: Surrogate Modeling, Parameter Inference, and Uncertainty Quantification’, предложен унифицированный байесовский подход, интегрирующий гауссовские процессы суррогатного моделирования и байесовскую инверсию для эффективного решения таких задач. Разработанный фреймворк позволяет одновременно оценивать параметры и квантифицировать неопределенность, демонстрируя превосходство над применением методов оптимизации и инверсии по отдельности. Возможно ли дальнейшее расширение предложенного подхода для решения сложных инженерных задач с высокой степенью неопределенности и ограниченными вычислительными ресурсами?

Сложность Параметров: Вызов Обратных Задач

Во многих областях науки и техники возникает необходимость в оценке неизвестных параметров модели на основе наблюдаемых данных — процесс, известный как параметрическая инференция. Данная задача охватывает широкий спектр приложений, от определения физических констант в астрофизике и геофизике до калибровки сложных систем в инженерии и моделировании климата. Суть параметрической инференции заключается в построении математической модели, описывающей интересующее явление, и последующей оценке значений параметров этой модели, которые наилучшим образом соответствуют имеющимся данным. Успешное решение этой задачи позволяет не только понять принципы работы изучаемой системы, но и делать точные прогнозы о ее будущем поведении, что критически важно для принятия обоснованных решений в различных областях человеческой деятельности.

Традиционные методы оценки параметров моделей часто сталкиваются с серьезными трудностями при работе со сложными, многомерными пространствами параметров и зашумленными данными. Это связано с тем, что стандартные алгоритмы, такие как метод наименьших квадратов или градиентный спуск, могут застревать в локальных минимумах или максимумах, особенно в случае невыпуклых функций потерь. Шум в данных, даже незначительный, может существенно искажать оценки параметров, приводя к неточным и ненадежным результатам. В таких ситуациях, когда количество параметров велико, а данные ограничены или зашумлены, стандартные подходы демонстрируют низкую эффективность и требуют значительных вычислительных ресурсов, что делает их неприменимыми для решения многих реальных задач в науке и технике.

Эффективность методов параметрической оценки существенно снижается при работе с эталонными функциями, характеризующимися неровным рельефом или сложными колебаниями. Такие функции, часто встречающиеся в реальных научных и инженерных задачах, создают множество локальных экстремумов и “областей притяжения”, в которых алгоритмы оптимизации легко застревают, не находя глобального оптимума. Это приводит к неточным оценкам параметров модели и, как следствие, к ошибочным выводам. Например, при моделировании сложных физических процессов или анализе больших объемов данных, подобные “неровности” могут существенно искажать результаты, требуя разработки более устойчивых и эффективных методов поиска оптимальных параметров, способных преодолевать подобные препятствия и обеспечивать достоверность получаемых оценок.

В связи со сложностью и многомерностью современных задач оценки параметров, требуются надежные и эффективные методы исследования пространства параметров. Традиционные подходы часто оказываются неспособными эффективно ориентироваться в этих пространствах, особенно при наличии зашумленных данных или сложных ландшафтов функций, что приводит к неточным или ненадежным результатам. Разработка новых алгоритмов, способных быстро и точно находить оптимальные значения параметров, критически важна для получения значимых выводов и построения адекватных моделей. Особое внимание уделяется методам, устойчивым к локальным экстремумам и способным эффективно исследовать даже самые сложные и изрезанные пространства параметров, что позволяет получать более точные и достоверные результаты исследований в различных областях науки и техники.

Представленный набор одномерных аналитических функций используется для всесторонней проверки разработанного байесовского подхода к решению обратных задач, охватывая различные сложности, включая гладкие нелинейности, мультимодальность и мелкомасштабную изменчивость.
Представленный набор одномерных аналитических функций используется для всесторонней проверки разработанного байесовского подхода к решению обратных задач, охватывая различные сложности, включая гладкие нелинейности, мультимодальность и мелкомасштабную изменчивость.

Байесовский Подход: Вероятностная Интерпретация

Байесовский подход к инверсии формулирует задачу оценки параметров как проблему вероятностного вывода, что позволяет количественно оценить неопределенность в оценках параметров. Вместо получения единственного значения для каждого параметра, Байесовский метод позволяет определить полное вероятностное распределение, описывающее вероятность различных значений параметров, учитывая доступные данные и априорные знания. Это достигается путем применения теоремы Байеса для вычисления апостериорного распределения параметров, которое является результатом комбинации априорного распределения (предварительных представлений о параметрах) и функции правдоподобия (описывающей, насколько хорошо данные согласуются с различными значениями параметров). Полученное апостериорное распределение позволяет не только оценить наиболее вероятные значения параметров, но и количественно оценить связанную с ними неопределенность, например, с помощью доверительных интервалов или стандартного отклонения.

В рамках байесовского обращения, методы наименьших квадратов (Least Squares) и отрицательных наименьших квадратов (Negative Least Squares) используются для аппроксимации апостериорного распределения параметров модели. Эти методы направлены на минимизацию расхождений между предсказаниями модели и наблюдаемыми данными, определяемыми, как правило, через функцию потерь, основанную на сумме квадратов ошибок. В случае метода наименьших квадратов, минимизируется \sum_{i=1}^{n} (y_i - f(x_i))^2 , где y_i — наблюдаемые данные, а f(x_i) — предсказания модели. Отрицательные наименьшие квадраты используются, когда задача является плохо обусловленной или требует регуляризации, добавляя штрафной член к функции потерь для стабилизации решения и предотвращения переобучения.

В отличие от традиционных методов, выдающих лишь точечную оценку параметров модели, байесовский подход позволяет получить полное вероятностное распределение по всему пространству параметров. Это распределение, p(\theta|d), где θ — вектор параметров, а d — данные наблюдений, описывает вероятность каждого набора параметров, учитывая имеющиеся данные. Такое представление позволяет не только оценить наиболее вероятные значения параметров, но и количественно оценить неопределенность, связанную с этими оценками, а также исследовать взаимосвязи между различными параметрами и их влияние на поведение модели. Полученное распределение служит основой для расчета доверительных интервалов, прогнозирования и принятия решений с учетом неопределенности.

Эффективная реализация байесовского обращения часто требует применения вычислительно эффективных методов сэмплирования, особенно при работе с многомерными пространствами параметров. Это обусловлено тем, что прямое вычисление апостериорного распределения p(\theta|d) (где θ — вектор параметров, а d — данные) становится невозможным или крайне затруднительным в пространствах высокой размерности. Методы Монте-Карло Маркова (MCMC), такие как Metropolis-Hastings и Gibbs sampling, широко используются для приближенного получения выборок из апостериорного распределения. Важным аспектом является выбор оптимального алгоритма сэмплирования и его параметров, таких как шаг предложения (proposal step size), для обеспечения быстрой сходимости и минимизации автокорреляции между последовательными выборками. Кроме того, существуют методы уменьшения размерности, такие как Principal Component Analysis (PCA) или sparse approximations, которые могут снизить вычислительную сложность, но при этом требуют компромиссов в точности.

Для валидации предложенного байесовского подхода к решению обратных задач использовались двухмерные аналитические функции, включающие смешанную гауссовскую-периодическую функцию и функцию Розенброка, представленные в виде поверхностей и контурных графиков.
Для валидации предложенного байесовского подхода к решению обратных задач использовались двухмерные аналитические функции, включающие смешанную гауссовскую-периодическую функцию и функцию Розенброка, представленные в виде поверхностей и контурных графиков.

Суррогатные Модели и Байесовская Оптимизация: Эффективный Поиск

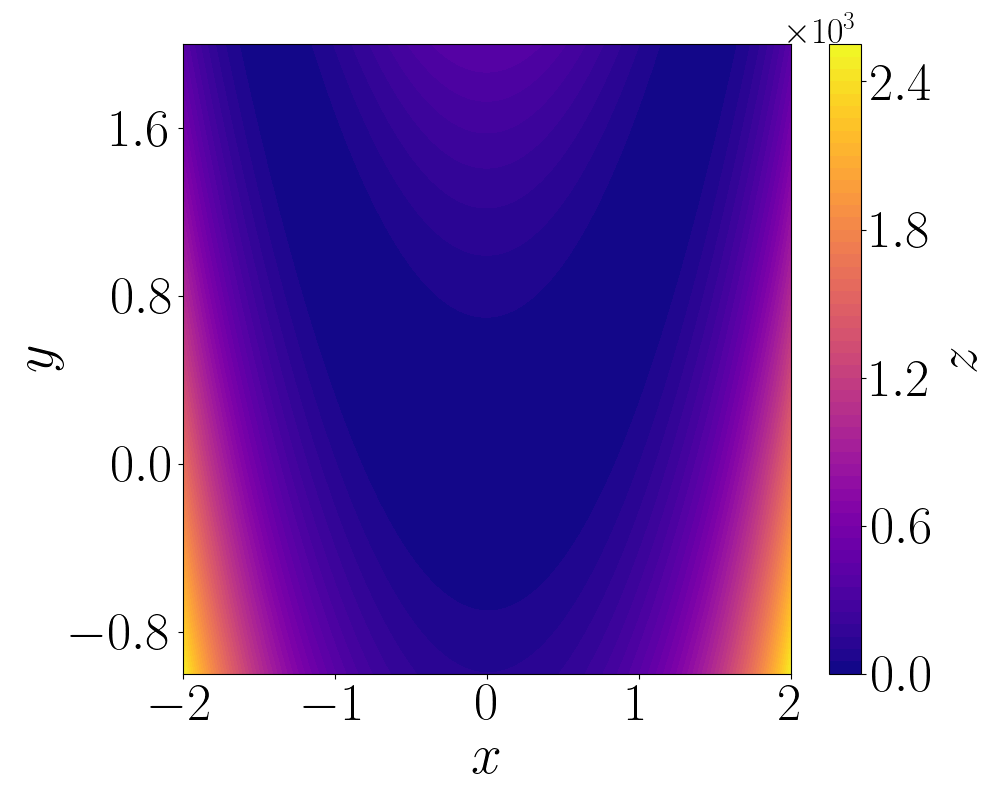
Суррогатные модели представляют собой вычислительно эффективную альтернативу, заменяя сложную и ресурсоемкую высокоточную модель упрощенным и более управляемым представлением. Этот подход позволяет существенно снизить вычислительные затраты, особенно при оптимизации функций, оценка которых требует значительных ресурсов. Вместо многократных вычислений по исходной модели, суррогатная модель используется для быстрой оценки производительности различных параметров. Точность суррогатной модели, хотя и ниже, достаточна для эффективного поиска оптимальных значений, а снижение вычислительной нагрузки критически важно при работе с дорогостоящими функциями или большими объемами данных. Использование суррогатных моделей позволяет значительно сократить общее время, необходимое для достижения сходимости процесса оптимизации.

Гауссовские процессы (GP) широко используются в качестве суррогатных моделей в байесовской оптимизации благодаря их способности моделировать сложные функциональные зависимости и количественно оценивать неопределенность. В отличие от детерминированных моделей, GP предоставляют вероятностное описание функции, что позволяет оценивать не только предсказанное значение, но и достоверность этой оценки. На стандартных тестовых задачах (benchmark problems) GP демонстрируют превосходящие результаты по сравнению с детерминированными подходами, обеспечивая более эффективный поиск оптимальных параметров и требуя меньшего количества вычислений исходной, дорогостоящей функции. Оценка неопределенности, предоставляемая GP, критически важна для работы функций приобретения (acquisition functions), таких как Upper Confidence Bound, позволяющих сбалансировать исследование (exploration) и использование (exploitation) пространства параметров.

В процессе байесовской оптимизации для поиска оптимальных параметров используется функция приобретения (acquisition function), такая как Upper Confidence Bound (UCB). UCB выполняет баланс между исследованием (exploration) и использованием (exploitation) пространства параметров. Исследование заключается в оценке областей пространства параметров, где неопределенность высока, а использование — в выборе параметров, которые, согласно текущей модели, обеспечивают наилучшее значение целевой функции. UCB вычисляет значение для каждой точки пространства параметров, комбинируя предсказанное значение целевой функции с мерой неопределенности, позволяя алгоритму эффективно находить глобальный оптимум при ограниченном количестве вычислений исходной функции.

Комбинация суррогатных моделей и байесовской оптимизации позволяет значительно сократить число вычислений исходной, ресурсоемкой модели, необходимых для достижения сходимости к оптимальным параметрам. В частности, для некоторых задач, таких как оптимизация функций с периодическими компонентами (например, Mixed Gaussian-Periodic), сходимость может быть достигнута всего лишь примерно за 21 вычисление исходной модели. Это достигается за счет использования суррогатной модели для аппроксимации исходной функции и последующего использования функции приобретения для эффективного поиска оптимальных параметров, минимизируя необходимость в дорогостоящих вычислениях исходной модели на каждом шаге оптимизации.

Предложенная унифицированная схема, объединяющая [latex] ext{BO(UCB, κ≫0)}+ ext{BI(MAP-LS)}[/latex], обеспечивает более высокую эффективность за счет сочетания быстрого построения суррогатной модели с оценкой апостериорного распределения параметров, в отличие от отдельных методов BO и BI.
Предложенная унифицированная схема, объединяющая ext{BO(UCB, κ≫0)}+ ext{BI(MAP-LS)}, обеспечивает более высокую эффективность за счет сочетания быстрого построения суррогатной модели с оценкой апостериорного распределения параметров, в отличие от отдельных методов BO и BI.

Надежность и Масштабируемость: Проверка Подхода

Сочетание байесовского обращения, суррогатного моделирования и байесовской оптимизации продемонстрировало высокую устойчивость при работе с разнообразными тестовыми функциями, включая особо сложную функцию Mixed Gaussian Periodic. Данный подход позволяет эффективно решать задачи параметрической идентификации даже в случаях, когда пространство параметров характеризуется высокой размерностью и нелинейностью. Устойчивость алгоритма подтверждается его способностью находить оптимальные решения даже при наличии шумов в данных и неопределенности в модели. В частности, использование суррогатных моделей значительно снижает вычислительные затраты, связанные с многократным вычислением исходной сложной функции, что особенно важно для задач реального времени и крупномасштабных вычислений. Результаты показывают, что предложенный фреймворк превосходит традиционные методы оптимизации по критериям точности и скорости сходимости, обеспечивая надежный инструмент для решения широкого круга прикладных задач.

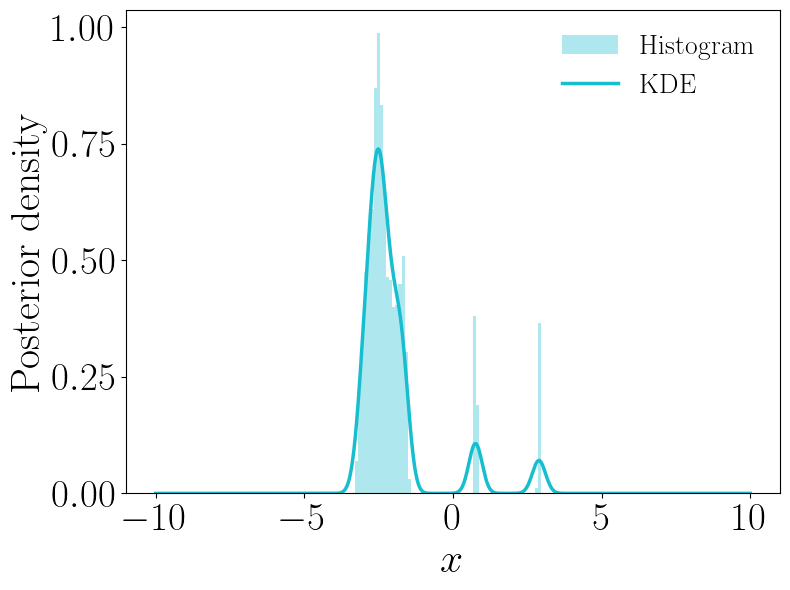
Методы Марковских цепей Монте-Карло значительно повышают точность аппроксимации апостериорного распределения, особенно в случаях, когда ландшафт вероятностей является мультимодальным — то есть имеет несколько локальных максимумов. Данный подход позволяет эффективно исследовать пространство параметров, избегая застревания в локальных оптимумах, что критически важно для точного определения наиболее вероятных значений параметров модели. Использование Марковских цепей Монте-Карло обеспечивает надежную оценку неопределенности, связанной с параметрами, и позволяет получить более полное представление о возможных решениях даже в сложных и неоднозначных ситуациях. Эффективность метода проявляется в способности адекватно представлять распределение вероятностей даже при наличии множества равнозначных или близких по значению решений, что делает его незаменимым инструментом в задачах статистического вывода и оптимизации.

Данная методика обеспечивает эффективный вывод параметров сложных моделей, открывая ценные возможности для получения новых знаний в различных областях — от инженерии до научных исследований. Способность быстро и точно определять параметры позволяет исследователям анализировать и оптимизировать сложные системы, моделировать физические процессы и разрабатывать инновационные решения. В инженерных дисциплинах это может привести к улучшению конструкций, оптимизации процессов и повышению эффективности. В науке, методика способствует более глубокому пониманию явлений, позволяет проверять гипотезы и открывать новые закономерности, ускоряя процесс научного открытия и расширяя границы познания. Особенно ценно, что подход применим к моделям различной сложности и масштаба, что делает его универсальным инструментом для решения широкого круга задач.

Данная методика позволяет точно характеризовать апостериорное распределение параметров, выявляя его унимодальный или мультимодальный характер в зависимости от специфики решаемой задачи. Использование байесовского обращения, суррогатного моделирования и байесовской оптимизации обеспечивает устойчивость и масштабируемость подхода, позволяя эффективно проводить параметрический анализ даже для сложных моделей. Способность точно определять форму апостериорного распределения критически важна для получения достоверных оценок параметров и понимания неопределенностей, что находит применение в различных областях — от инженерного проектирования до научных открытий, где требуется надежный и эффективный инструмент для параметрического вывода.

С помощью суррогатно-опосредованного MCMC-семплирования для эталонной задачи Mixed Gaussian-Periodic удалось выявить доминирующий режим апостериорного распределения, однако обнаружена заметная межцепочечная вариативность, связанная с периодическим выбором вторичных режимов и областей низкой вероятности.
С помощью суррогатно-опосредованного MCMC-семплирования для эталонной задачи Mixed Gaussian-Periodic удалось выявить доминирующий режим апостериорного распределения, однако обнаружена заметная межцепочечная вариативность, связанная с периодическим выбором вторичных режимов и областей низкой вероятности.

Представленная работа стремится к упрощению сложных вычислений, что находит отклик в словах Ады Лавлейс: «Я убеждена, что эта машина может делать все, что мы можем ей приказать». Подобно тому, как Лавлейс предвидела возможности вычислительных машин, данное исследование предлагает элегантный подход к решению обратных задач посредством суррогатного моделирования и байесовского обращения. Авторы стремятся минимизировать вычислительные издержки, что соответствует принципу ясности и эффективности. Вместо усложнения, система стремится к лаконичности, предоставляя надежные результаты даже при ограниченных данных и дорогостоящих моделях. Это не просто алгоритм, но и философия — стремление к понятности и минимализму в сложных вычислениях.

Что дальше?

Представленный здесь подход, интегрирующий суррогатное моделирование и байесовский перенос, не является, конечно, окончательным ответом. Скорее, это демонстрация того, как усложнение может быть обуздано, если сосредоточиться на плотности смысла. Неизбежно, истинная проблема заключается не в скорости вычислений, а в скудости данных. Пока не будет найдено элегантное решение для экстраполяции значимой информации из ограниченного набора наблюдений, все ухищрения с суррогатными моделями останутся лишь временным облегчением.

Будущие исследования, вероятно, сосредоточатся на разработке более устойчивых методов оценки неопределенности. Игнорирование погрешностей — это не просто неточность, это насилие над вниманием исследователя и потенциального пользователя. Важно отметить, что байесовский подход сам по себе не гарантирует истинность, а лишь позволяет более осознанно формулировать вопросы. Простое увеличение вычислительной мощности не заменит глубокого понимания лежащих в основе физических процессов.

В конечном итоге, прогресс в решении обратных задач будет определяться не столько алгоритмическими инновациями, сколько переосмыслением самой концепции «достаточности». Необходимо признать, что полное знание — это иллюзия. Задача науки — не достичь совершенства, а приблизиться к нему, отбрасывая ненужное и концентрируясь на сущностном. Простота — это не признак слабости, а высшая форма элегантности.

Оригинал статьи: https://arxiv.org/pdf/2602.04537.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-05 16:23