Геометрия данных: Оптимизация кинетики плазмы с помощью иерархического подхода

Автор: Денис Аветисян

В статье представлена методика, использующая структуру данных для эффективной настройки параметров моделей кинетики плазмы, даже при ограниченном объеме данных.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Использование иерархических методов оптимизации демонстрирует улучшенную сходимость функции потерь [latex]\Phi_{train}[/latex] и повышенную эффективность выборки в начальной фазе обучения, особенно при варьировании размерности подпространства [latex]k[/latex], при этом анализ спектра собственных значений [latex]{\lambda_{i}}[/latex] гессиана Гаусса-Ньютона [latex]H_{GN} = V\Lambda V^{T}[/latex] выявляет наличие — Использование иерархических методов оптимизации демонстрирует улучшенную сходимость функции потерь $\Phi_{train}$ и повышенную эффективность выборки в начальной фазе обучения, особенно при варьировании размерности подпространства $k$ , при этом анализ спектра собственных значений ${\lambda_{i}}$ гессиана Гаусса-Ньютона $H_{GN} = V\Lambda V^{T}$ выявляет наличие «жесткого» подпространства $V_{0}$ и «рыхлого» подпространства, определяющих поведение алгоритма в окрестности найденного минимума ${\theta_{final}}$ .

Предложен новый иерархический алгоритм оптимизации, основанный на анализе данных и геометрии пространства параметров, применимый к задачам кинетики плазмы и моделированию взаимодействия плазмы с поверхностью.

Несмотря на растущую сложность физических моделей, точная калибровка параметров часто сдерживается вычислительными затратами и ограниченностью экспериментальных данных. В данной работе, посвященной ‘Stochastic hierarchical data-driven optimization: application to plasma-surface kinetics’, предложен новый стохастический иерархический подход к оптимизации, использующий принципы теории «неуклюжих» моделей для эффективного поиска параметров в высокоразмерном пространстве. Ключевым элементом является аппроксимация гессиана, позволяющая идентифицировать и использовать наиболее чувствительные параметры с минимальным количеством вычислений кинетических моделей плазмы и поверхности. Позволит ли данная методика существенно ускорить разработку и валидацию моделей сложных реакционных систем, от плазменной химии до биохимических сетей?

Вызов Высокой Размерности в Моделировании Плазмы

Точное моделирование кинетики плазмы требует оценки значительного количества параметров, что обуславливает вычислительную сложность задачи оптимизации. Каждый параметр, описывающий процессы и характеристики плазмы — от плотности частиц и температуры электронов до скоростей химических реакций на поверхности — вносит вклад в общую картину, и его точное определение критически важно для получения достоверных результатов. Однако, увеличение числа параметров экспоненциально увеличивает вычислительные затраты, делая традиционные методы оптимизации неэффективными и требуя разработки новых подходов для преодоления этой проблемы. Это особенно актуально при моделировании сложных плазменных процессов, где необходимо учитывать множество взаимодействующих факторов и оптимизировать параметры для достижения требуемой точности прогнозирования.

Традиционные методы оптимизации сталкиваются с серьезными трудностями при моделировании плазмы из-за сложности и многомерности ландшафта функции потерь. Это обусловлено огромным количеством параметров, которые необходимо оценить для точного описания кинетики плазмы, что приводит к неэффективности стандартных алгоритмов поиска оптимальных значений. В результате, точность предсказания вероятности поверхностной рекомбинации, ключевого параметра в плазменных процессах, оказывается ограниченной. Например, типичные модели демонстрируют коэффициент детерминации $R^2$ всего 0.736, что указывает на существенное расхождение между предсказанными и экспериментальными данными и подчеркивает необходимость разработки более эффективных методов оптимизации для решения этой сложной задачи.

Оптимизированная кинетическая модель демонстрирует высокую точность предсказания [latex]\gamma_{O}[/latex] (коэффициент поверхностного натяжения), подтвержденную сильной корреляцией (R² = 0.736) и улучшенным соответствием экспериментальным данным при различных температурах и давлениях по сравнению с использованием параметров по умолчанию. — Оптимизированная кинетическая модель демонстрирует высокую точность предсказания $\gamma_{O}$ (коэффициент поверхностного натяжения), подтвержденную сильной корреляцией (R² = 0.736) и улучшенным соответствием экспериментальным данным при различных температурах и давлениях по сравнению с использованием параметров по умолчанию.

Использование Структуры Модели: “Небрежные” Модели и Обучение на Многообразиях

Многие физические системы, включая кинетику плазмы, демонстрируют поведение, характеризуемое как «небрежная модель» (sloppy model). Это означает, что изменение большинства параметров модели оказывает незначительное влияние на выходные данные системы. Фактически, лишь небольшое число направлений в параметрическом пространстве существенно влияет на результат, в то время как остальные направления могут изменяться без существенного изменения поведения системы. Данное явление обусловлено высокой чувствительностью системы к изменениям вдоль этих ключевых направлений и низкой чувствительностью к изменениям в остальных направлениях, что позволяет значительно упростить анализ и моделирование сложных систем.

Методы обучения на многообразиях позволяют выявить скрытое, низкоразмерное пространство, определяющее поведение модели, что существенно снижает вычислительную нагрузку. Традиционные методы оптимизации и анализа часто сталкиваются с проблемой «проклятия размерности» при работе с моделями, имеющими большое количество параметров. Использование алгоритмов, таких как изометрическое отображение (Isomap), локальное линейное вложение (LLE) или t-SNE, позволяет спроецировать высокоразмерные данные в пространство меньшей размерности, сохраняя при этом важные структурные характеристики. Это приводит к уменьшению числа параметров, требующих оптимизации, и снижает сложность вычислений, особенно в задачах, связанных с поиском оптимальных значений параметров модели или анализом чувствительности к изменениям входных данных. В результате, скорость и эффективность моделирования значительно возрастают, что делает возможным анализ более сложных систем и получение результатов в разумные сроки.

Несмотря на потенциально большое количество параметров в модели, эффективное число степеней свободы, определяющих её поведение, часто ограничено. Это связано с тем, что многие параметры оказывают незначительное влияние на выходные данные, а изменение лишь небольшого подмножества параметров приводит к существенным изменениям в результатах. Уменьшение размерности пространства параметров, фокусировка на наиболее влиятельных направлениях, позволяет упростить процесс оптимизации, снизить вычислительные затраты и повысить эффективность поиска оптимальных значений параметров модели. Такой подход особенно актуален для сложных систем, где полный перебор параметров невозможен или непрактичен.

Иерархическая Оптимизация со Стратегией Уменьшенного Гессиана

В рамках оптимизации была реализована иерархическая стратегия, разделяющая пространство параметров на “жесткие” (stiff) и “рыхлые” (sloppy) направления. “Жесткие” направления характеризуются высокой кривизной функции потерь и оказывают существенное влияние на результат оптимизации, поэтому основная вычислительная мощность направляется именно на их обработку. Такое разделение позволяет снизить вычислительные затраты, поскольку “рыхлые” направления, оказывающие незначительное влияние на функцию потерь, оптимизируются с меньшей точностью. Данный подход позволяет эффективно использовать ресурсы и ускорить процесс поиска оптимальных параметров модели.

Для эффективного определения “жестких” направлений в пространстве параметров используется стратегия пониженного Гессиана, основанная на аппроксимации Госса-Ньютона. Данный подход позволяет вычислить приближение Гессиана, используя только первые производные функции потерь, что значительно снижает вычислительную сложность по сравнению с вычислением полного Гессиана. Аппроксимация Госса-Ньютона, выраженная как $J^T J$ , где $J$ — матрица Якоби, обеспечивает достаточно точную оценку кривизны функции потерь вдоль этих направлений, позволяя сконцентрировать усилия оптимизации на наиболее чувствительных параметрах и ускорить процесс сходимости.

Применение предложенного метода иерархической оптимизации демонстрирует более высокую скорость сходимости и устойчивость оценки параметров по сравнению с традиционными алгоритмами, такими как Trust Region Reflective, Powell’s Method, Covariance Matrix Adaptation Evolution Strategy, Differential Evolution и Gaussian Processes. В ходе тестирования удалось достичь сопоставимой тестовой ошибки с алгоритмом Trust Region Reflective, при этом потребовалось значительно меньшее количество вычислений модели — симуляций. Это позволяет снизить вычислительные затраты и повысить эффективность оптимизации в задачах, требующих высокой точности и скорости.

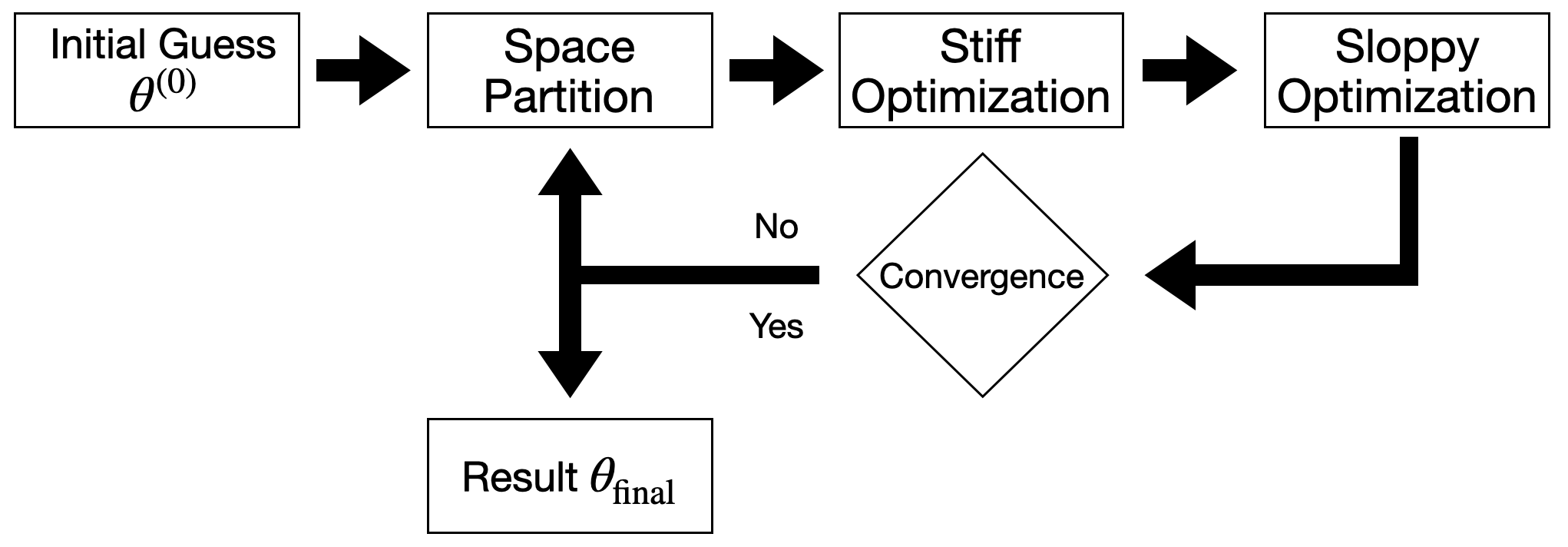
Иерархический алгоритм позволяет эффективно декомпозировать сложную задачу на более простые подзадачи, что упрощает её решение.

Подтверждение и Значение для Моделирования Кинетики Плазмы

Исследование продемонстрировало значительное повышение точности и эффективности оценки параметров модели кинетики плазмы благодаря применению разработанного иерархического метода оптимизации. Используя экспериментальный набор данных, включающий 225 стационарных состояний, удалось не только более надежно определить значения параметров, но и существенно сократить вычислительные затраты. Подобный подход позволяет получать более реалистичные и точные прогнозы поведения плазмы, что особенно важно для моделирования сложных процессов и оптимизации технологических режимов, применяемых в различных отраслях промышленности, включая микроэлектронику и материаловедение.

Полученные в ходе исследования значения параметров позволяют значительно точнее прогнозировать вероятность рекомбинации на поверхности, что углубляет понимание процессов, происходящих во взаимодействии плазмы и твердой поверхности. Более точная оценка вероятности рекомбинации критически важна для моделирования поведения плазмы в различных технологических процессах, включая травление, осаждение и модификацию материалов. Улучшенное понимание этих взаимодействий открывает возможности для оптимизации технологических параметров и повышения эффективности плазменной обработки в различных отраслях промышленности, от микроэлектроники до материаловедения. Точное определение этого параметра способствует более адекватному описанию процессов, происходящих на границе раздела фаз, и позволяет разрабатывать более эффективные стратегии управления плазмой.

В ходе исследования была проведена количественная оценка неопределенности для 29 параметров плазменной кинетики с использованием гессиана — матрицы вторых частных производных. Этот подход позволил выделить так называемые “жесткие” параметры, незначительное изменение которых приводит к существенным изменениям в модели, и “мягкие” параметры, более устойчивые к вариациям. Выявление подобной чувствительности параметров имеет важное практическое значение, поскольку позволяет оптимизировать плазменные технологии, используемые в различных промышленных процессах, например, при травлении и осаждении тонких пленок. Повышенная точность моделирования, основанная на учете неопределенности параметров, способствует более эффективному управлению плазменными процессами и, как следствие, улучшению качества производимой продукции.

Результаты 5-кратной кросс-валидации показали, что оптимизированные медианные значения стерических факторов [latex]k_{0,30}[/latex] (выделены цветом для жестких параметров: серый - десорбция, синий - хемосорбция CO, розовый - метастабильные энергии) значительно отличаются от стандартных литературных значений (зеленый цвет), в то время как параметры с низкой чувствительностью остаются неизменными, что подтверждается границами неопределенности, полученными из гессиана. — Результаты 5-кратной кросс-валидации показали, что оптимизированные медианные значения стерических факторов $k_{0,30}$ (выделены цветом для жестких параметров: серый — десорбция, синий — хемосорбция CO, розовый — метастабильные энергии) значительно отличаются от стандартных литературных значений (зеленый цвет), в то время как параметры с низкой чувствительностью остаются неизменными, что подтверждается границами неопределенности, полученными из гессиана.

Исследование демонстрирует, что упрощение сложных систем, сохраняя при этом ключевые характеристики, является ключом к эффективной оптимизации. Авторы подходят к проблеме, используя иерархическую структуру, что позволяет им сосредоточиться на наиболее чувствительных параметрах и снизить вычислительную сложность. Этот подход перекликается с мыслями Давида Гильберта: «В математике не существует простого пути». Однако, в данном контексте, ‘простота’ достигается не за счет отказа от сложности, а за счет её осознанной организации и управления. Успешное применение метода к кинетике плазмы-поверхности подтверждает, что хорошо спроектированная система, основанная на понимании внутренней геометрии модели, действительно масштабируется лучше, чем чрезмерно изощренная.

Куда Далее?

Представленная работа, касающаяся стохастической иерархической оптимизации, лишь приоткрывает дверь в область, где сложность модели и ограниченность данных неизбежно сталкиваются. Если система кажется сложной, она, вероятно, хрупка, и предложенный подход, использующий геометрию физических моделей, является попыткой навести порядок в этом хаосе. Однако, упрощение всегда требует жертв: какие аспекты кинетики плазмы-поверхности были намеренно опущены ради вычислительной эффективности? Этот вопрос остаётся открытым.

Перспективы очевидны: расширение набора инструментов для анализа «рыхлых» моделей, углублённое исследование структуры пространства параметров, и, что наиболее важно, разработка методов, позволяющих оценивать степень адекватности упрощённой модели реальному физическому процессу. Архитектура — это искусство выбора того, чем пожертвовать, но эта жертва должна быть осознанной и обоснованной. Оптимизация, как и любое искусство, требует не только мастерства, но и критической самооценки.

В конечном итоге, успех подобных подходов будет определяться не столько математической элегантностью алгоритмов, сколько способностью извлекать полезную информацию из скудных данных. Представленная работа — это не конец пути, а лишь очередная веха на пути к пониманию сложных систем. И, возможно, самое важное — это помнить, что даже самая совершенная модель — лишь приближение к реальности.

Оригинал статьи: https://arxiv.org/pdf/2602.04975.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-07 02:14