Робототехника: Новый подход к управлению движением

Автор: Денис Аветисян

Исследователи предложили оригинальный метод оптимизации обратной кинематики, объединяющий аналитические и численные подходы для повышения эффективности и скорости вычислений.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал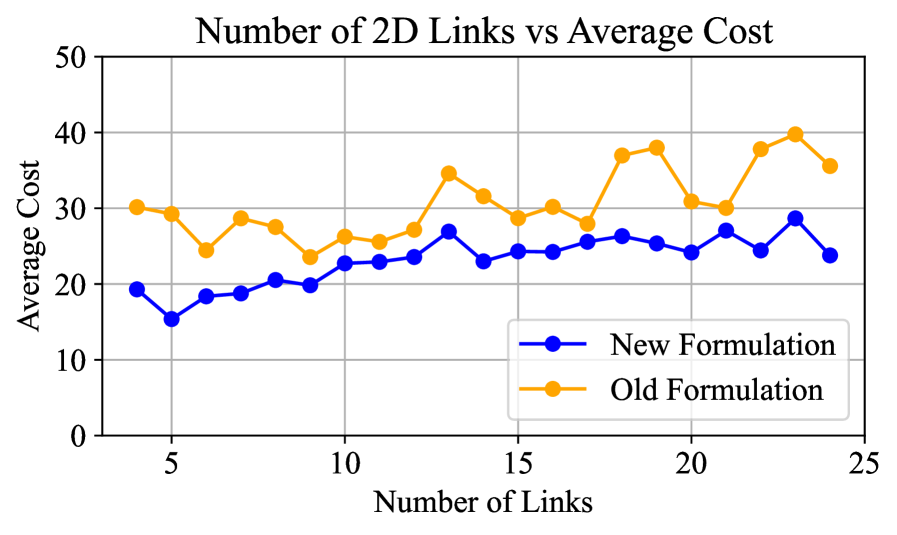

Результаты анализа кинематической схемы двухзвенного механизма, представленные для старой и новой формулировок, демонстрируют улучшение точности и стабильности решения обратной кинематики за счёт оптимизации алгоритма.

Предлагается фреймворк, использующий аналитические решения обратной кинематики в качестве преобразования переменных для упрощения задач нелинейной оптимизации.

Несмотря на глубокое изучение аналитических и оптимизационных методов решения задач обратной кинематики, объединение их сильных сторон остается сложной задачей. В работе, озаглавленной ‘A Framework for Combining Optimization-Based and Analytic Inverse Kinematics’, предложен новый подход к оптимизационной обратной кинематике, использующий аналитическое решение в качестве преобразования переменных. Это позволяет упростить задачу оптимизации и повысить ее эффективность, особенно при наличии невыпуклых ограничений, таких как избежание столкновений. Экспериментальные результаты демонстрируют, что предложенная методика превосходит существующие подходы в решении сложных задач обратной кинематики, включая захват объектов и обеспечение устойчивости гуманоидных роботов; не открывает ли это путь к созданию более надежных и адаптивных роботизированных систем?

Кинематика и Рабочее Пространство: Взгляд Вглубь Механизма

Определение возможностей робота начинается с детального описания его кинематической структуры посредством параметров Денавита-Хартенберга (DH). Эти параметры, представляющие собой систему координат, прикрепленных к каждой оси и соединению робота, позволяют математически описать геометрию манипулятора. $^{t}T_{i}$ — преобразование координат от системы координат {i} к системе координат {t} — является ключевым элементом, описывающим взаимное расположение звеньев робота. Использование параметров DH не только упрощает моделирование и анализ движения, но и обеспечивает стандартный подход к описанию кинематики различных робототехнических систем, позволяя инженерам эффективно проектировать, моделировать и контролировать сложные манипуляторы.

Параметры Денавита-Хартенберга позволяют вычислить прямую кинематику — то есть, определить положение и ориентацию концевого эффектора робота, исходя из углов его сочленений. Этот процесс является фундаментальным для управления роботом, поскольку он устанавливает точную связь между заданными углами поворота моторов и фактическим положением инструмента в пространстве. Более того, эти параметры определяют рабочую область робота — объем пространства, куда может достичь его концевой эффектор. Анализ рабочей области критически важен при проектировании робототехнических систем, поскольку позволяет оценить, сможет ли робот выполнить необходимые операции в заданном окружении и избежать столкновений с препятствиями. Знание рабочей области и прямой кинематики является необходимым условием для планирования траекторий движения и обеспечения эффективной и безопасной работы робота.

Роботы, обладающие избыточными степенями свободы, демонстрируют способность к самодвижению, что создает как уникальные сложности, так и значительные возможности в планировании траектории. В отличие от роботов с фиксированным числом степеней свободы, избыточные системы могут достигать одной и той же конечной точки различными способами, позволяя оптимизировать движение по различным критериям — избегать препятствий, минимизировать энергопотребление или поддерживать оптимальную ориентацию инструмента. Однако, поиск оптимального решения в пространстве избыточных конфигураций требует сложных алгоритмов и вычислительных ресурсов. Эффективное планирование движения для таких роботов предполагает не только достижение целевой позиции, но и управление избыточными степенями свободы для обеспечения дополнительной гибкости и адаптивности в динамически меняющейся среде. Это открывает перспективы для создания роботов, способных выполнять сложные задачи с повышенной точностью и надежностью, особенно в условиях ограниченного пространства или при взаимодействии с непредсказуемыми объектами.

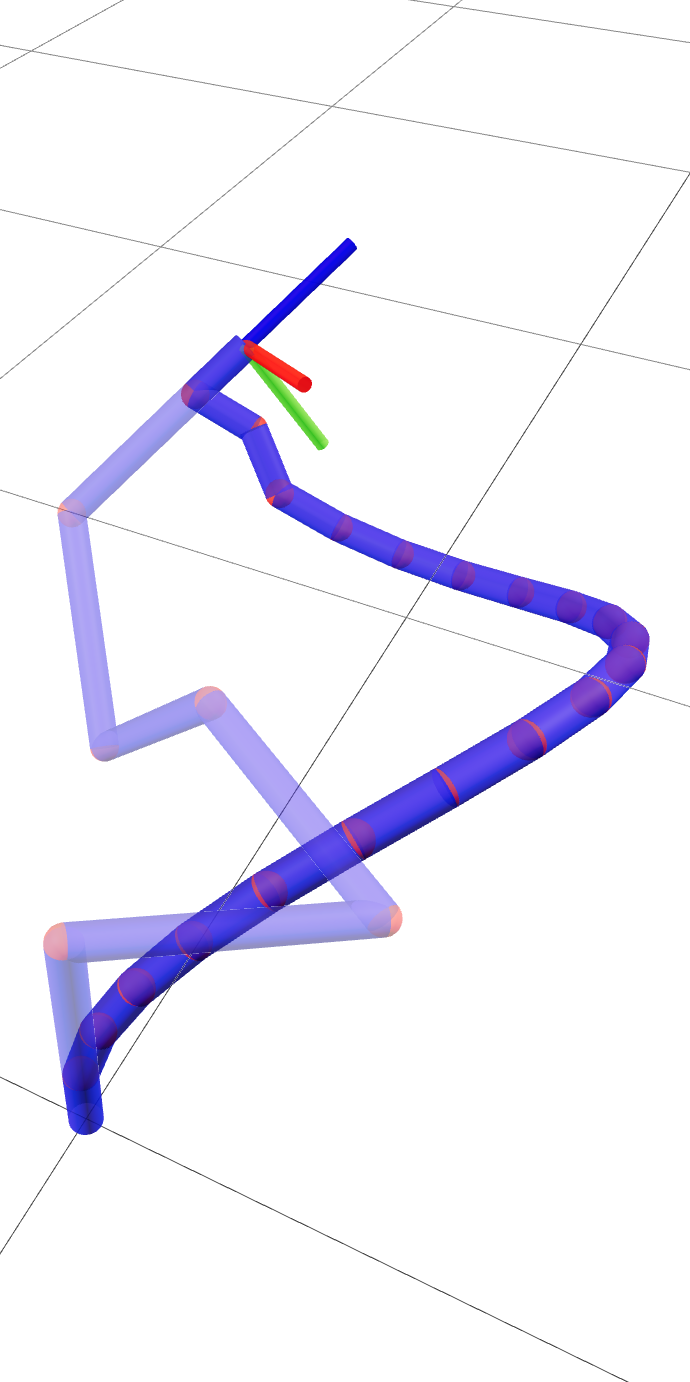
В ходе робосимуляций мы использовали различные конфигурации захвата и позиционирования, включая три доступные позы для экспериментов с выбором захвата, стабильную конфигурацию для робота Hubo и масштабируемую систему с манипуляторами различной степени свободы для решения задач обратной кинематики.

Безопасное Движение: Стратегии Предотвращения Столкновений

Предотвращение столкновений является критически важной задачей в робототехнике, поскольку потенциальные столкновения могут привести к повреждению оборудования, прерыванию работы и даже угрозе безопасности. Для обеспечения надежного функционирования роботов необходимо использовать надежные методы обнаружения потенциальных столкновений до их возникновения. Эти методы включают в себя сенсорные системы, такие как лидары, камеры и ультразвуковые датчики, которые предоставляют информацию об окружающей среде. Обработка данных, полученных от этих датчиков, требует сложных алгоритмов для определения расстояния до препятствий и прогнозирования потенциальных траекторий столкновения. Эффективность системы предотвращения столкновений напрямую зависит от скорости обработки данных, точности сенсоров и способности алгоритмов предсказывать поведение окружающей среды и самого робота.

Для эффективного определения близости к препятствиям в робототехнике широко используются методы, основанные на выпуклых оболочках и знаковых расстояниях. Выпуклая оболочка — это минимальная выпуклая фигура, содержащая заданное множество точек, представляющих объект. Расстояние от точки до объекта вычисляется как кратчайшее расстояние до поверхности этой выпуклой оболочки. Знаковое расстояние указывает, находится ли точка внутри или снаружи объекта; положительное значение обычно указывает на внешнюю область, а отрицательное — на внутреннюю. Использование этих методов позволяет упростить сложные геометрические формы и быстро оценить риск столкновения, поскольку вычисление расстояний до выпуклых поверхностей значительно менее затратно, чем для произвольных поверхностей.

Метод «Покрытие кликами» (Clique Cover) позволяет формировать политопы, свободные от столкновений, что является основой для проактивного планирования траектории робота. Суть метода заключается в разложении пространства препятствий на набор клик — полносвязных подграфов, представляющих области, где столкновения невозможны. Для каждого клика вычисляется допустимая траектория, а затем эти траектории объединяются для создания глобального, свободного от столкновений пути. Эффективность метода зависит от размера клик и сложности пространства препятствий, однако он обеспечивает гарантированно безопасное планирование движения в сложных окружениях, особенно в задачах, где требуется учитывать динамические препятствия и ограничения робота.

Обратная Кинематика: От Позы к Углам Сочленений

Обратная кинематика (ОК) представляет собой процесс вычисления углов, необходимых для суставов манипулятора (или другого механизма) для достижения заданной позы (положения и ориентации) его рабочего органа. Входными данными для ОК служат желаемое положение и ориентация рабочего органа в пространстве, а выходными — значения углов, которые необходимо установить на каждом суставе, чтобы достичь этой позы. Данный процесс является ключевым для управления роботами и другими механизмами, поскольку он позволяет определить, как двигать суставы, чтобы рабочий орган достиг требуемой цели. Решение задачи ОК не всегда однозначно, и может существовать несколько комбинаций углов суставов, приводящих к одной и той же позе рабочего органа.

Существуют различные методы решения задачи обратной кинематики (ОК), варьирующиеся от аналитических решений до подходов, основанных на оптимизации. Аналитические методы, применимые к простым кинематическим цепям, предоставляют быстрый расчет углов суставов в закрытой форме. Однако, для более сложных роботов или при наличии ограничений на углы и скорости, аналитические решения могут быть невозможны. В таких случаях применяются методы, основанные на оптимизации, которые формулируют задачу ОК как задачу оптимизации, минимизирующую ошибку между желаемым положением и положением, полученным при заданных углах суставов. Эти методы позволяют учитывать различные ограничения и критерии, но требуют больших вычислительных ресурсов.

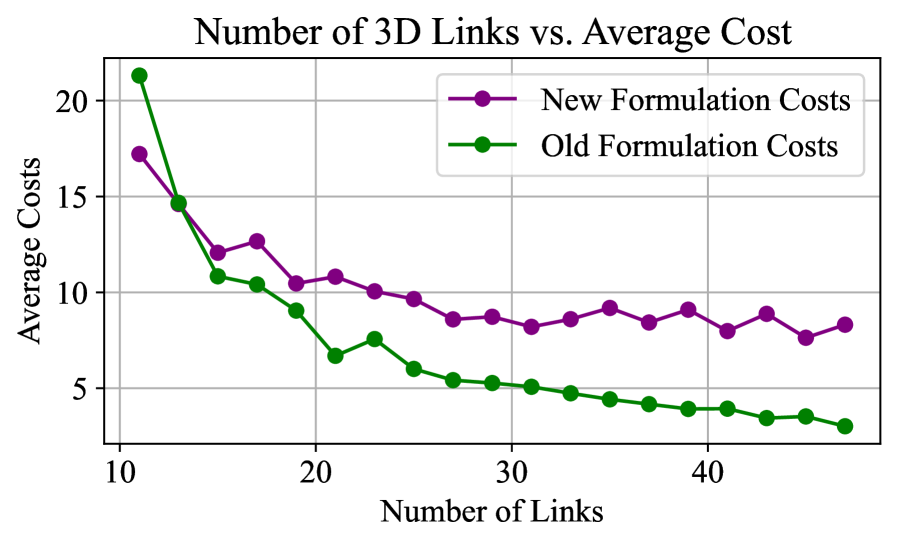
Оптимизационные методы обратной кинематики (Optimization-IK и Global_IK) используют преимущества выпуклой оптимизации для обеспечения надежных решений, в то время как аналитическая обратная кинематика (Analytic_IK) предоставляет быстрые, замкнутые решения, когда это возможно. В ходе экспериментов, включающих манипуляции с манипулятором на столе, выбор захвата, двуручное управление и обеспечение устойчивости гуманоидного робота, разработанная нами оптимизационная формулировка обратной кинематики продемонстрировала равную или более высокую вероятность успешного решения по сравнению со стандартными подходами. Это указывает на повышенную устойчивость и эффективность предложенного метода в различных сценариях роботизированных задач.

Новая формулировка обратной кинематики для трехмерной цепи звеньев демонстрирует улучшенные результаты по сравнению с предыдущей.

Ограничения Движения Робота: Стабильность и Пределы

Метод Constraint_IK направлен на решение сложных задач, связанных с обеспечением выполнения различных кинематических ограничений для роботов. Эти ограничения включают в себя пределы допустимых углов поворота суставов, а также предотвращение столкновений робота с окружающими объектами и самим собой. Обеспечение соблюдения этих условий критически важно для безопасной и эффективной работы робота в реальных условиях. Сложность заключается в том, что одновременное удовлетворение множества ограничений может приводить к неразрешимым задачам, требующим продвинутых алгоритмов оптимизации и учета динамических свойств робота. Эффективное решение подобных задач позволяет значительно расширить область применения роботов и повысить их надежность.

Стабильность робота играет ключевую роль в обеспечении надежной и предсказуемой работы. Поддержание устойчивого положения требует учета множества факторов, включая распределение массы, положение центра тяжести и воздействие внешних сил. Исследования показывают, что даже незначительные отклонения от устойчивого состояния могут привести к потере равновесия и, как следствие, к сбоям в выполнении задач или даже к повреждениям. Поэтому, алгоритмы, обеспечивающие стабильность, являются неотъемлемой частью управления роботами, особенно в динамичных средах и при выполнении сложных манипуляций. Обеспечение устойчивости не только гарантирует безопасность, но и позволяет роботу работать с большей точностью и эффективностью, расширяя спектр решаемых задач.

Обеспечение надёжного и предсказуемого поведения робота напрямую зависит от эффективного учёта различных ограничений, таких как пределы перемещения суставов и предотвращение столкновений. Разработанный подход позволяет значительно повысить точность соблюдения этих ограничений, что особенно важно для сложных задач, требующих поддержания стабильной позы. Упрощение оптимизационной среды, достигаемое благодаря данной методике, облегчает наложение даже самых жёстких ограничений, обеспечивая безопасность и надёжность работы робота в различных сценариях. Благодаря этому, становится возможным реализовывать более сложные и точные движения, минимизируя риски и повышая эффективность выполнения поставленных задач.

Разнообразные решения, полученные в экспериментах с Hubo с использованием различных формулировок и представлений ограничений устойчивости, демонстрируют эффективность оптимизатора IPOPT.

Исследование представляет собой интересный подход к решению задачи обратной кинематики, преобразуя её, по сути, в другую задачу с более управляемым набором ограничений. Авторы предлагают использовать аналитические решения обратной кинематики как своего рода преобразование координат, что позволяет упростить процесс оптимизации. Этот метод, в некотором смысле, напоминает взлом системы: вместо прямого решения сложной задачи, она разбивается на более мелкие, легко преодолимые этапы. Как однажды заметил Роберт Тарьян: «Программное обеспечение — это как секс: раньше или позже, кто-то обязательно найдёт в нём ошибку». И в данном случае, «ошибка» — это сложность исходной задачи, которую авторы ловко обходят, используя элегантное преобразование переменных.

Что дальше?

Представленный подход к решению обратной кинематики, использующий аналитические решения как преобразование переменных, обнажает закономерность: каждый «патч» в алгоритмах — это не столько исправление ошибок, сколько философское признание фундаментальной неидеальности систем. Упрощение задачи путем изменения её представления — это, по сути, взлом самой концепции сложности. Но где предел этому упрощению? Всегда ли возможно свести многомерную проблему к более простой, не потеряв при этом критически важную информацию?

Очевидно, что эффективность предложенного метода напрямую зависит от качества и доступности аналитических решений. В тех случаях, когда аналитическое решение отсутствует или слишком вычислительно затратно, выгода от оптимизационного подхода может быть нивелирована. Будущие исследования должны быть направлены на разработку гибридных стратегий, умело сочетающих сильные стороны как аналитических, так и оптимизационных методов, возможно, с использованием методов машинного обучения для автоматического выбора оптимальной стратегии решения.

В конечном итоге, задача обратной кинематики — это лишь частный случай более общей проблемы — нахождения решений в сложных, многомерных пространствах. Истинный прогресс заключается не в создании все более изощренных алгоритмов, а в глубоком понимании структуры этих пространств и принципов, управляющих ими. Лучший «хак» — это осознание того, как всё работает, и умение использовать эти знания для обхода ограничений и достижения желаемого результата.

Оригинал статьи: https://arxiv.org/pdf/2602.05092.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-07 10:25