Игры разума: новый подход к планированию в мультиагентных системах

Автор: Денис Аветисян

Исследователи предлагают метод разложения динамических игр, позволяющий оптимизировать стратегии для роботов в условиях асимметричной информации.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

В процессе обучения многослойный перцептрон (MLP) формирует стратегию [latex]\pi_{\theta}[/latex] посредством минимизации трех различных функций потерь, после чего, на основе полученной стратегии и динамики системы игрока 2, аппроксимируется наилучший ответ [latex]\widehat{\mathcal{B}}_{2}[/latex], что позволяет решить предложенное упрощенное условие Каруша-Куна-Таккера (KKT) с использованием суррогата этого ответа. — В процессе обучения многослойный перцептрон (MLP) формирует стратегию $\pi_{\theta}$ посредством минимизации трех различных функций потерь, после чего, на основе полученной стратегии и динамики системы игрока 2, аппроксимируется наилучший ответ $\widehat{\mathcal{B}}_{2}$ , что позволяет решить предложенное упрощенное условие Каруша-Куна-Таккера (KKT) с использованием суррогата этого ответа.

В статье представлена методика вычисления равновесия Нэша в динамических играх посредством реструктуризации задачи и замены онлайн-оптимизации на заранее скомпилированное ограничение выполнимости.

Вычисление равновесий в динамических играх, необходимых для моделирования многоагентных систем, часто затруднено сложностью условий оптимальности и плохой вычислительной устойчивостью. В данной работе, ‘A Data Driven Structural Decomposition of Dynamic Games via Best Response Maps’, предложен принципиально новый подход к решению этой проблемы, основанный на структурной декомпозиции игры и замене онлайн-блока оптимизации на оффлайн-скомпилированное ограничение, заданное картой наилучших ответов. Такой подход позволяет снизить вычислительную сложность и повысить надежность планирования в условиях асимметричной информации, гарантируя нахождение локального открытого равновесия Нэша. Возможно ли дальнейшее расширение предложенного метода для решения задач с большим числом агентов и более сложными динамическими моделями?

Временные Игры: Основы Динамического Взаимодействия

Многие реальные ситуации, от экономических торгов до биологических взаимодействий и даже политических стратегий, характеризуются наличием нескольких агентов, чьи действия тесно взаимосвязаны и оказывают влияние друг на друга. В таких сценариях, где исход для каждого участника зависит не только от его собственных решений, но и от выборов других, применение традиционных методов анализа часто оказывается недостаточным. Именно поэтому возникает необходимость в рамках динамических игр — математических моделей, позволяющих учитывать эту взаимозависимость и прогнозировать поведение агентов во времени. Данный подход позволяет исследовать сложные стратегии, возникающие в условиях конкуренции и сотрудничества, и находить оптимальные решения в ситуациях, где успех одного участника может зависеть от действий других.

Равновесие Нэша представляет собой фундаментальное понятие в теории динамических игр, обозначающее стабильное состояние, в котором ни одному участнику не выгодно в одностороннем порядке менять свою стратегию, учитывая стратегии остальных. Представьте ситуацию, где каждый игрок выбрал свой оптимальный ход, и любое отклонение от него приведёт к ухудшению результата — это и есть равновесие Нэша. Это не означает, что результат обязательно оптимален для всех участников в совокупности, но гарантирует, что каждый игрок действует рационально, исходя из действий других. $\text{max}_{s_i} u_i(s_i, s_{-i}) \text{ при условии } s_{-i} \text{ фиксировано}$ — эта математическая формулировка отражает суть: каждый игрок максимизирует свою выгоду $u_i$ при фиксированных стратегиях остальных игроков $s_{-i}$ . Понимание равновесия Нэша необходимо для анализа широкого спектра ситуаций, от экономических торгов до биологической эволюции и даже политических переговоров, позволяя предсказывать стабильные исходы в условиях стратегического взаимодействия.

Традиционные решения, основанные на понятии равновесия Нэша, сталкиваются с существенными трудностями при моделировании сложных динамических систем. Вычислительная сложность поиска такого равновесия экспоненциально возрастает с увеличением числа агентов и возможных стратегий, что делает точное решение практически невозможным для реалистичных сценариев. Эта проблема усугубляется тем, что равновесие Нэша предполагает совершенную рациональность всех участников, что редко встречается на практике. В результате, применение классических методов часто требует упрощений, которые снижают адекватность модели, или же приводит к необходимости использования приближенных алгоритмов и эвристик, жертвуя точностью ради вычислительной эффективности. Поиск альтернативных подходов, способных эффективно справляться с вычислительными ограничениями и учитывать неполную информацию, является ключевой задачей в современной теории игр.

Предложенный метод успешно генерирует парные траектории для игроков 1 (красный) и 2 (синий) при различных начальных условиях.

Обобщенные Равновесия и Допустимость Решений

Обобщенное равновесие Нэша (Generalized Nash Equilibrium, GNE) является расширением классического равновесия Нэша, предназначенным для динамических систем, в которых состояния и управляющие воздействия отдельных агентов взаимосвязаны. В стандартном равновесии Нэша предполагается, что стратегии игроков не влияют на состояния других игроков. Однако в динамических системах, таких как автономное вождение или управление робототехническими системами, действия одного агента могут изменять состояние среды, что, в свою очередь, влияет на стратегии и результаты других агентов. GNE учитывает эти зависимости, определяя состояние равновесия как набор стратегий, в котором ни один агент не может улучшить свою функцию полезности, изменив свою стратегию, учитывая стратегии других агентов и динамику системы. Это требует решения более сложной задачи оптимизации, чем в классическом случае, поскольку необходимо учитывать как стратегические взаимодействия, так и динамику системы, описываемую, например, дифференциальными уравнениями.

Поиск обобщенных равновесий часто сводится к решению сложных задач оптимизации, ограниченных различными условиями. Для определения допустимых решений в таких задачах используются ограничения допустимости (Feasibility Constraints). Эти ограничения задают множество значений переменных, удовлетворяющих определенным требованиям, таким как физические границы, ограничения на ресурсы или технические характеристики системы. Например, в задачах управления движением, ограничения допустимости могут включать максимальную скорость, ускорение, углы поворота или ограничения на траекторию. Использование ограничений допустимости позволяет сузить пространство поиска решений и обеспечить реалистичность и выполнимость полученных результатов. Решение задач оптимизации с ограничениями допустимости обычно требует применения специализированных алгоритмов и численных методов.

Для точного моделирования окружающей среды в задачах управления движением часто требуются упрощающие допущения. Кинематическая модель велосипеда ( $\text{Kinematic Bicycle Model}$ ) представляет собой упрощенное, но эффективное представление динамики транспортного средства, широко используемое в планировании траекторий и управлении. Она позволяет анализировать движение автомобиля как велосипеда, рассматривая только основные степени свободы — положение и ориентацию. В сочетании с траекториями постоянной кривизны ( $\text{Constant-Curvature Tracks}$ ), эта модель обеспечивает вычислительно эффективный способ проверки реализуемости и оптимизации управляющих воздействий, сохраняя при этом достаточно высокую степень адекватности реальным условиям движения.

Стратегии Оптимизации: Учет Взаимосвязей в Совместной Системе

В динамических играх, взаимодействие между агентами формирует так называемую объединенную систему (Joint-Coupled System). Это означает, что стратегия каждого агента напрямую влияет на оптимальную стратегию всех остальных, и, следовательно, для достижения стабильного равновесия необходимо одновременное рассмотрение стратегий всех участников. Игнорирование взаимосвязей между агентами и последовательное решение задач оптимизации для каждого из них может привести к неоптимальным результатам и нестабильности системы в целом. Такая система характеризуется тем, что оптимальное решение для одного агента зависит от решений всех остальных, что требует итеративных методов решения и учета взаимных ограничений.

Онлайн-оптимизация вложенных циклов (Online Nested Optimization) представляет собой итеративный подход к решению систем, возникающих при взаимодействии агентов в динамических играх. В рамках данного подхода, оптимизация стратегий всех агентов осуществляется совместно на каждой итерации. Однако, сложность вычислений при этом быстро возрастает с увеличением числа агентов и размерности пространства стратегий. Это обусловлено необходимостью решения большого числа оптимизационных задач на каждой итерации, что приводит к значительным затратам вычислительных ресурсов и времени, особенно в задачах с высокой размерностью и сложными ограничениями. Вследствие этого, прямое применение онлайн-оптимизации вложенных циклов может быть непрактичным для задач реального времени или задач, требующих высокой скорости вычислений.

Для снижения вычислительной нагрузки в процессе решения системы, связанной с взаимодействием агентов, используется упрощенная система KKT (Karush-Kuhn-Tucker). Данный подход включает в себя учет ограничений допустимости, что позволяет значительно сократить объем вычислений. Согласно результатам, полученным в ходе Монте-Карло моделирования, применение упрощенной системы KKT обеспечивает 70%-ный уровень успешного решения задачи. $\text{Success Rate} = 0.70$ Эффективность метода подтверждена статистически и позволяет повысить скорость и масштабируемость алгоритмов, используемых в динамических играх с множеством взаимодействующих агентов.

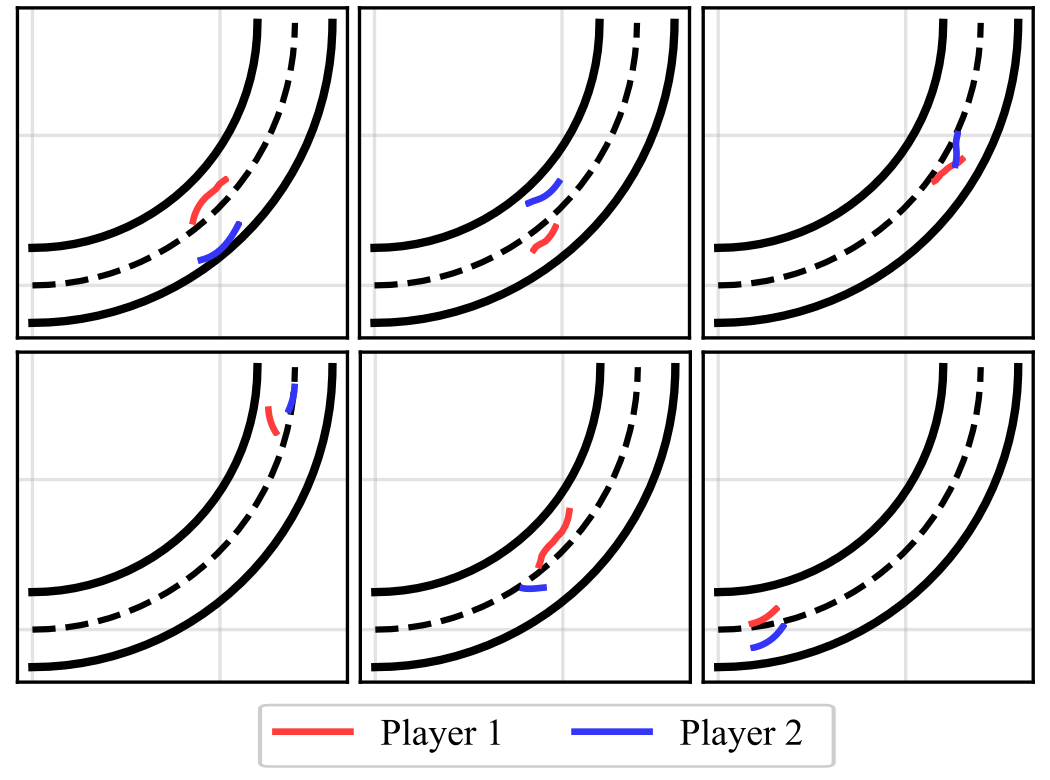
Сравнение с базовыми алгоритмами, использующими полную информацию, на [latex]N=1200[/latex] Monte Carlo сценариях показало, что предложенный метод демонстрирует сопоставимое количество итераций и минимальный запас коллизий при успешном выполнении, а также меньшую разницу в стоимости [latex] \Delta J\_{1}:=J\_{1}^{\mathrm{ours}}-J\_{1}^{\mathrm{base}} [/latex] по сравнению с базовыми алгоритмами, при этом обеспечивая сопоставимое количество успешных и неуспешных попыток. — Сравнение с базовыми алгоритмами, использующими полную информацию, на $N=1200$ Monte Carlo сценариях показало, что предложенный метод демонстрирует сопоставимое количество итераций и минимальный запас коллизий при успешном выполнении, а также меньшую разницу в стоимости $\Delta J\_{1}:=J\_{1}^{\mathrm{ours}}-J\_{1}^{\mathrm{base}}$ по сравнению с базовыми алгоритмами, при этом обеспечивая сопоставимое количество успешных и неуспешных попыток.

Основанные на Данных Подходы: Изучение Поведения Агентов

Представление о наилучшей стратегии агента, определяемой картой наилучших реакций, предполагает знание оптимальных действий в ответ на действия других участников. Однако, в сложных динамических системах, явное определение этой карты становится практически невозможным из-за экспоненциального роста вычислительной сложности с увеличением числа игроков и доступных действий. Необходимость учитывать все возможные комбинации стратегий оппонентов быстро приводит к неразрешимой задаче, что делает традиционный подход непрактичным для анализа и моделирования реальных сценариев взаимодействия. В связи с этим, возникает потребность в альтернативных методах, позволяющих приблизительно оценить наилучшие реакции агента без необходимости полного перебора всех возможных ситуаций.

Предлагается новый подход к определению оптимальной стратегии агента в сложных динамических играх, основанный на построении Data-Driven Best-Response Surrogate — модели, обучаемой на основе наблюдаемых данных. Вместо явного определения карты оптимальных ответов, что часто оказывается невозможным из-за вычислительной сложности, данная модель аппроксимирует эту карту, используя информацию, полученную из реальных взаимодействий агентов. Это позволяет эффективно вычислять стратегии агентов, значительно снижая вычислительные затраты и обеспечивая масштабируемость решений для широкого спектра игровых сценариев. В результате, достигается возможность быстрого и точного определения оптимальных действий агента даже в условиях высокой сложности и неопределенности.

Разработанный суррогат, основанный на упрощенной системе условий Каруша-Куна-Таккера (KKT), обеспечивает эффективное вычисление стратегий агентов, позволяя масштабировать решения для сложных динамических игр. Экспериментальные результаты, полученные в ходе 1200 Monte Carlo испытаний, демонстрируют медианное время решения успешных задач менее одной секунды, а общая доля успешно решенных задач составила 70%. При этом, система также способна эффективно выявлять невыполнимые сценарии, фиксируя такую ситуацию в 29.8% случаев, что подчеркивает ее надежность и практическую ценность в условиях ограниченных ресурсов и высокой сложности игровых взаимодействий.

Представленная работа демонстрирует стремление к созданию систем, способных достойно стареть в сложной среде динамических игр. Авторы предлагают подход, заменяющий онлайн-оптимизацию оффлайн-компиляцией ограничений по выполнимости, что позволяет повысить эффективность и надежность планирования в условиях асимметричной информации. Этот метод, по сути, создает своего рода ‘хронику жизни системы’, фиксируя допустимые состояния и позволяя агентам действовать в рамках этих ограничений. Как однажды заметил Брайан Керниган: «Простота — это высшая степень совершенства». В данном исследовании стремление к упрощению процесса вычисления равновесия Нэша посредством предкомпилированных ограничений напрямую соответствует этой идее, обеспечивая более элегантное и устойчивое решение для многоагентной робототехники.

Что дальше?

Представленная работа, стремясь к более эффективному вычислению равновесий Нэша в динамических играх, неизбежно сталкивается с фундаментальным вопросом: достаточно ли оптимизации, чтобы победить энтропию? Замена онлайн-оптимизации на офлайн-компилированное ограничение осуществимости — это не столько решение, сколько перенос бремени. Время, как среда, в которой существуют системы, не прощает задержек, и каждое упрощение несет в себе цену. Очевидно, что архитектура, лишенная исторической перспективы, неизбежно окажется хрупкой и недолговечной.

Необходимо осознавать, что асимметричная информация, остающаяся сложной задачей, не исчезает, а лишь маскируется. Поиск методов, позволяющих не просто учитывать, но и использовать неопределенность как ресурс, представляется более перспективным направлением. Следует уделить внимание не только вычислительной эффективности, но и робастности решений в условиях неполноты данных и возмущений.

В конечном счете, истинный прогресс заключается не в создании все более сложных алгоритмов, а в понимании пределов их применимости. Каждая задержка — цена понимания. Следующим шагом видится разработка мета-фреймворка, позволяющего адаптировать подходы к различным классам динамических игр, учитывая специфику конкретной задачи и ограничения среды. Все системы стареют — вопрос лишь в том, делают ли они это достойно.

Оригинал статьи: https://arxiv.org/pdf/2602.05324.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-07 17:09