Прогноз на миллиарды: Согласование и масштабирование

Автор: Денис Аветисян

Новые алгоритмы позволяют эффективно решать задачи согласования прогнозов в условиях огромных объемов данных, типичных для современной розничной торговли.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал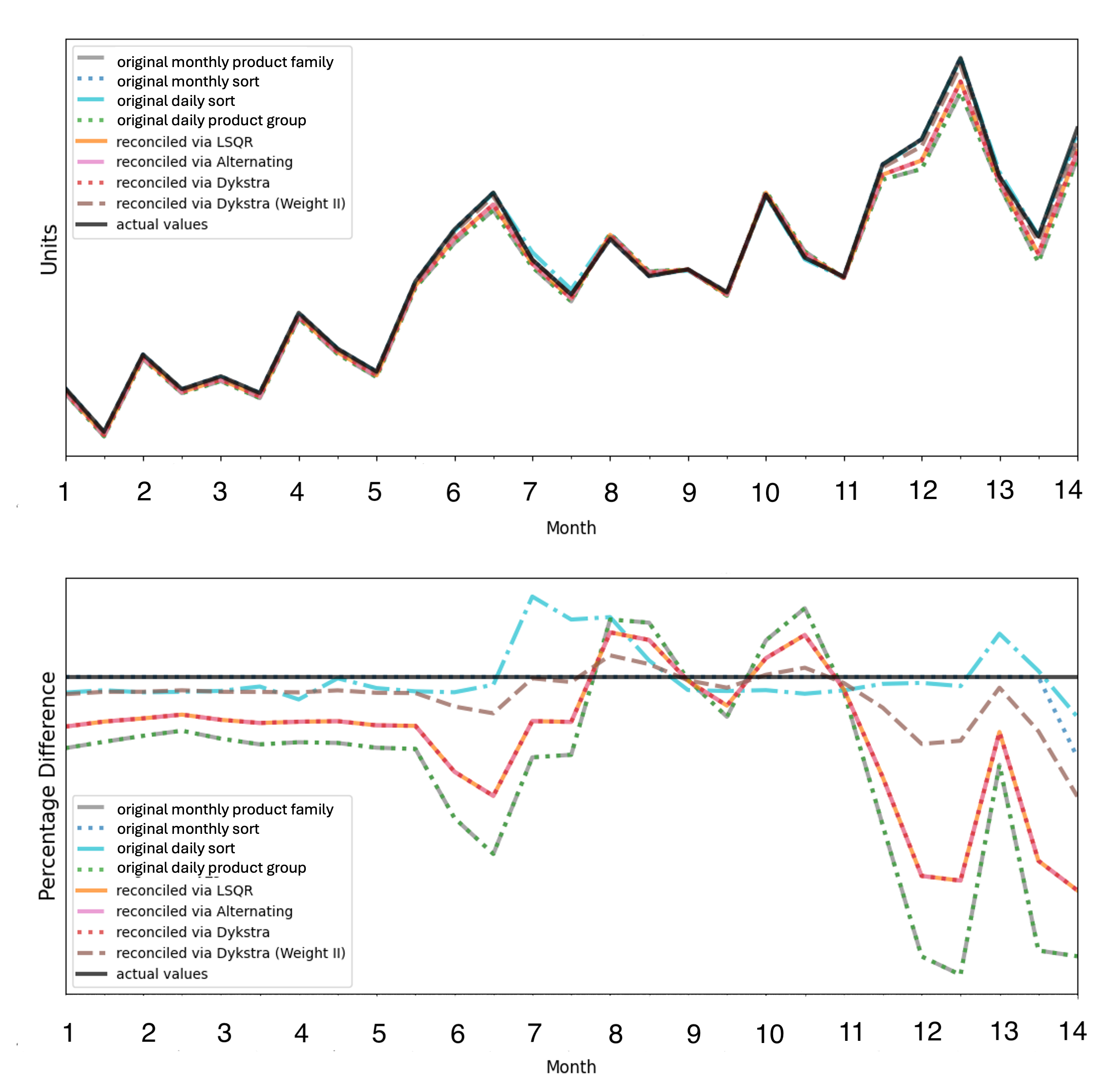

Наблюдения за крупным сегментом данных выявили, что сопоставление единиц измерения с течением месяцев позволяет оценить процентное расхождение от фактических значений, демонстрируя динамику отклонений во времени.

Исследование предлагает масштабируемые методы согласования иерархических прогнозов, основанные на квадратичном программировании и выпуклом оптимизационном подходе.

Согласование прогнозов по иерархическим временным рядам представляет собой сложную задачу, особенно при масштабировании до миллиардов параметров. В данной работе, посвященной ‘Billions-Scale Forecast Reconciliation’, предложены масштабируемые алгоритмы для решения этой проблемы, демонстрирующие эффективность в контексте крупномасштабного розничного прогнозирования. Показано, что предложенный оптимизационный подход к согласованию прогнозов эквивалентен методам, основанным на долях, для ограниченного класса задач, что формализует обобщение традиционных подходов. Смогут ли эти методы стать основой для еще более точного и эффективного планирования в сложных экономических системах?

Прогнозы как Экосистемы: Вызов Когерентности

Традиционные методы прогнозирования, несмотря на статистическую достоверность на уровне агрегированных данных, зачастую демонстрируют отсутствие согласованности при детализации до более низких уровней иерархии. Например, общий прогноз продаж для сети магазинов может быть точным, однако при распределении этого прогноза по отдельным магазинам могут возникнуть нереалистичные цифры — некоторые магазины покажут отрицательные продажи, или же общий объем продаж по всем магазинам не будет соответствовать исходному агрегированному прогнозу. Это несоответствие возникает из-за того, что стандартные подходы игнорируют взаимосвязи между уровнями иерархии, не учитывая, что изменения на верхнем уровне должны логически отражаться на нижних. В результате, несмотря на кажущуюся точность на глобальном уровне, детальные прогнозы могут оказаться бесполезными или даже вводящими в заблуждение для принятия управленческих решений.

Несоответствие в прогнозах часто возникает из-за того, что стандартные методы не учитывают логические связи, присущие иерархическим структурам данных. В результате, прогнозы на нижних уровнях иерархии могут оказаться нереалистичными или даже невозможными, поскольку не согласуются с общими прогнозами на верхних уровнях. Например, суммарный прогноз продаж по региону может быть точным, но при этом отдельные прогнозы для городов внутри этого региона могут противоречить друг другу или не соответствовать общей сумме. Эта проблема особенно актуальна при работе со сложными бизнес-структурами или временными рядами, где каждая часть иерархии зависит от других, и игнорирование этих взаимосвязей приводит к искажению общей картины и принятию неверных управленческих решений.

Необходимость методов, учитывающих взаимосвязи в иерархических данных, становится критически важной при анализе сложных бизнес-структур и временных рядов. Традиционные подходы к прогнозированию зачастую игнорируют логическую зависимость между элементами иерархии, что приводит к нереалистичным или попросту невозможным результатам на нижних уровнях детализации. Например, при прогнозировании продаж для сети магазинов, суммарный прогноз по всем магазинам может быть статистически обоснованным, однако прогнозы для отдельных магазинов, не учитывающие региональные особенности и взаимосвязи между ними, могут значительно отклоняться от реальности. В связи с этим, разработка и применение методов, способных поддерживать когерентность прогнозов на всех уровнях иерархии, представляется необходимым условием для эффективного планирования и принятия решений в сложных организационных системах.

Все алгоритмы, за исключением LSQR, решают одну и ту же задачу и, следовательно, дают идентичные скорректированные прогнозы, при этом LSQR, не имея ограничения неотрицательности, демонстрирует сопоставимые результаты для данного размера проблемы [latex]10^6 imes 408[/latex]. — Все алгоритмы, за исключением LSQR, решают одну и ту же задачу и, следовательно, дают идентичные скорректированные прогнозы, при этом LSQR, не имея ограничения неотрицательности, демонстрирует сопоставимые результаты для данного размера проблемы $10^6 imes 408$ .

Согласование Прогнозов: Иерархический Порядок

Методология согласования прогнозов предназначена для корректировки первоначальных прогнозов с целью удовлетворения предопределенных ограничений агрегации, обеспечивая согласованность на различных иерархических уровнях. Это означает, что суммарные прогнозы на нижних уровнях должны соответствовать прогнозам на верхних уровнях иерархии. Согласование прогнозов особенно важно в организациях с комплексными структурами, где общие показатели являются суммой показателей отдельных подразделений или продуктов. Отсутствие согласования может привести к нереалистичным или противоречивым прогнозам, что негативно скажется на планировании и принятии решений. Процесс предполагает использование математических алгоритмов для распределения общей величины прогноза между отдельными элементами иерархии с учетом заданных ограничений.

В основе метода согласования прогнозов лежит использование Матрицы Агрегации, которая определяет взаимосвязи между прогнозами на различных уровнях иерархии. Эта матрица задает, каким образом суммируются прогнозы нижнего уровня для формирования итоговых прогнозов на верхних уровнях. Каждый элемент матрицы отражает вес, с которым конкретный прогноз нижнего уровня вносит вклад в итоговый прогноз. Например, матрица может указывать, что прогноз продаж для конкретного продукта (нижний уровень) напрямую влияет на прогноз продаж для соответствующей категории продуктов (верхний уровень), а общие прогнозы продаж по категориям формируют общий прогноз продаж для всей компании. Точное определение этой матрицы является критически важным для обеспечения корректности и согласованности итоговых прогнозов.

Методика согласования прогнозов позволяет создавать реалистичные и внутренне согласованные прогнозы путем явного учета предопределенных агрегационных ограничений. Традиционные методы прогнозирования часто генерируют прогнозы на нижних уровнях иерархии, которые не соответствуют суммарным значениям на верхних уровнях, что приводит к несоответствиям и неточностям. Согласование прогнозов устраняет эти недостатки, обеспечивая соответствие между детальными прогнозами и агрегированными итогами, что повышает общую точность и надежность планирования. Использование матрицы агрегации позволяет систематически применять эти ограничения, гарантируя, что итоговые прогнозы соответствуют заданным иерархическим зависимостям.

Оптимизация Согласования: Поиск Наилучшего Баланса

Формулировка примирения прогнозов как задачи оптимизации обычно включает в себя минимизацию $Least Squares Problem$ , представляющей собой отклонение от исходных прогнозов. Данная задача заключается в поиске такого набора согласованных прогнозов, который минимизирует сумму квадратов разностей между итоговыми и исходными прогнозами по всем уровням иерархии. Минимизация $Least Squares Problem$ позволяет количественно оценить и уменьшить общую ошибку прогноза, обеспечивая согласованность между различными уровнями агрегации и повышая точность прогнозирования в целом. При этом, величина отклонения, минимизируемая в задаче, отражает степень несоответствия между прогнозами на разных уровнях и позволяет оценить качество полученного решения.

Для решения задачи минимизации отклонений в процессе примирения прогнозов применяются различные методы. К ним относятся методы квадратичного программирования, позволяющие найти оптимальное решение путем минимизации квадратичной целевой функции при заданных ограничениях. Альтернативой является регрессия на конус, представляющая собой подход, основанный на использовании конусов второго порядка. Кроме того, применяются итеративные алгоритмы, такие как алгоритм Дыкстры и метод чередующихся проекций, которые последовательно улучшают решение до достижения сходимости. Выбор конкретного метода зависит от сложности и структуры иерархии прогнозов, а также от требуемой вычислительной эффективности.

Выбор метода решения задачи примирения прогнозов напрямую зависит от сложности и требуемой вычислительной эффективности. Аналитические решения, или решения в замкнутой форме, являются оптимальными, когда это возможно, поскольку они обеспечивают прямое и быстрое вычисление. Однако, с увеличением иерархической структуры прогнозов и количества взаимосвязей между ними, вычислительная сложность аналитических решений экспоненциально возрастает, делая их непрактичными для масштабных задач. В таких случаях предпочтение отдается итеративным алгоритмам, таким как алгоритм Дыкстры или метод чередующихся проекций, а также методам квадратичного программирования и конусной регрессии, которые, хотя и требуют больше вычислительных ресурсов, обеспечивают масштабируемость и возможность решения сложных задач примирения прогнозов.

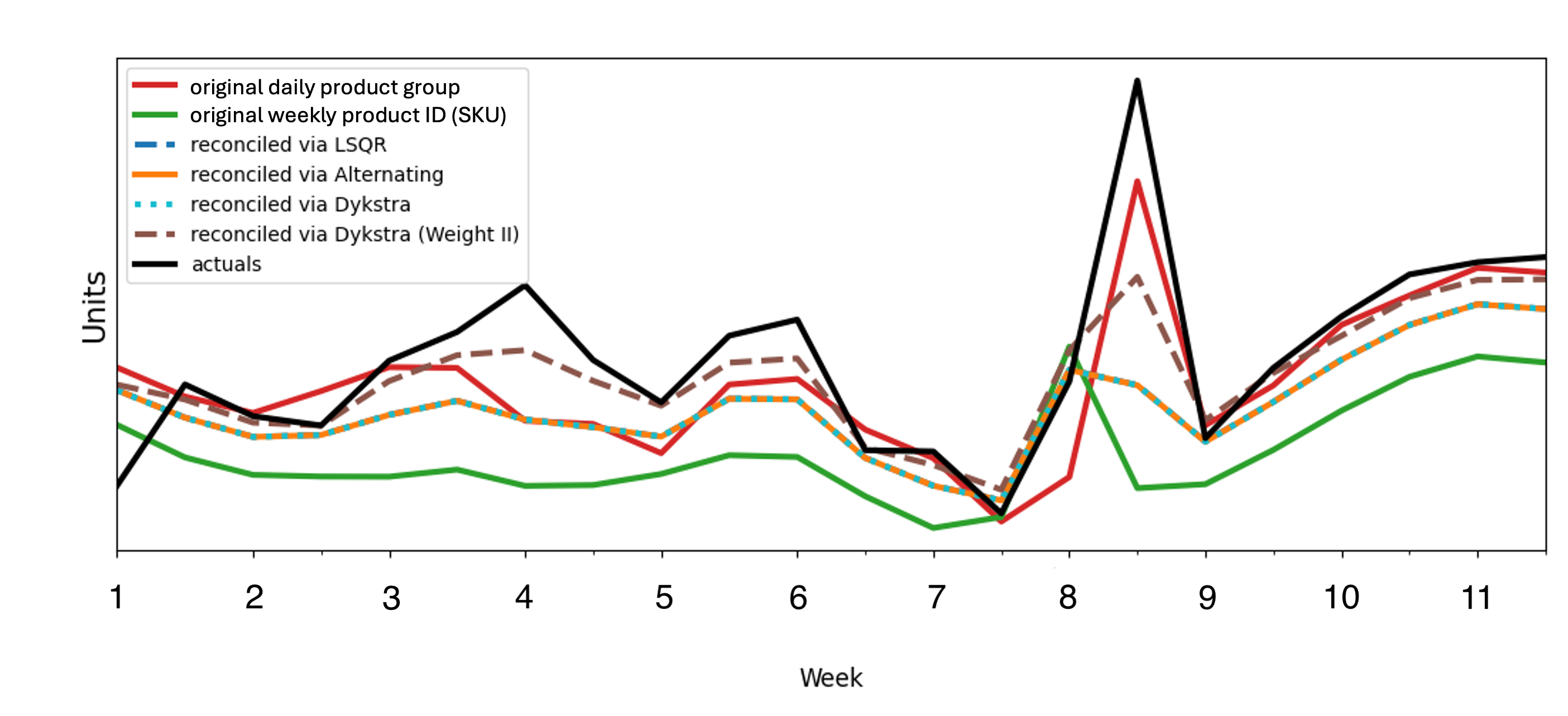
Визуализация демонстрирует успешную обработку сегмента данных большого объема (более 4 миллиардов элементов).

Взвешивание и Разреженное Представление: Управление Сложностью

Матрица весов играет ключевую роль в процессе согласования прогнозов, определяя степень влияния каждого отдельного прогноза на итоговый результат. Существуют различные стратегии взвешивания, среди которых выделяются “тяжелый верх” и “тяжелый низ”. Стратегия “тяжелый верх” (Top-Heavy Weighting) отдает приоритет прогнозам, полученным на верхних уровнях иерархии, что особенно полезно, когда общие тенденции имеют большее значение, чем детализация. В свою очередь, стратегия “тяжелый низ” (Bottom-Heavy Weighting) акцентирует внимание на прогнозах, сформированных на нижних уровнях, что может быть оправдано в ситуациях, когда важна высокая точность на уровне детализации. Выбор подходящей стратегии взвешивания напрямую влияет на качество согласования и, следовательно, на общую надежность прогнозов.

Представление матрицы весов в виде разреженной матрицы позволяет значительно снизить вычислительную нагрузку, особенно при работе с большими иерархиями прогнозов. В традиционных подходах, матрица весов, определяющая влияние различных прогнозов при их согласовании, хранит значения для каждой связи между уровнями иерархии. Однако, в реальных сценариях, многие из этих связей могут быть нулевыми или несущественными. Разреженная матрица, напротив, хранит только ненулевые элементы и их индексы, что существенно уменьшает объем необходимой памяти и количество операций. Этот подход становится критически важным при масштабировании, поскольку позволяет эффективно обрабатывать огромные объемы данных, например, в задачах с миллиардами прогнозов, где использование плотной матрицы весов становится практически невозможным из-за ограничений по ресурсам.

В контексте примирения прогнозов, помимо традиционных методов взвешивания, существуют специализированные подходы, такие как примирение на основе долей (Share-Based Reconciliation). Данные стратегии позволяют адаптировать веса в матрице агрегирования к специфике конкретного бизнеса и структуре иерархии прогнозов. Вместо равномерного или иерархического распределения влияния, примирение на основе долей учитывает вклад каждого элемента в общую картину, например, долю продукта в общем объеме продаж или долю региона в общей прибыли. Это позволяет создавать более точные и релевантные прогнозы, учитывающие уникальные особенности каждого сегмента и обеспечивающие оптимальное распределение ресурсов. Такой подход особенно ценен в сложных и многоуровневых иерархиях, где стандартные методы взвешивания могут приводить к значительным погрешностям.

Представленная работа демонстрирует успешное применение методов взвешивания и разреженных матриц для решения задачи согласования прогнозов беспрецедентного масштаба — 4 185 173 500 прогнозов. Для обработки столь огромного объема данных потребовалось управление матрицей агрегирования с размерами 47 213 x 4 185 173 500, что подчеркивает эффективность предложенных подходов в контексте больших данных. Успешная реализация и оптимизация алгоритмов позволила преодолеть вычислительные ограничения, характерные для задач подобного размаха, и продемонстрировать применимость этих методов к реальным бизнес-задачам, требующим обработки миллионов прогнозов.

Исследование демонстрирует, что попытки построить идеально предсказуемые системы обречены на провал. Авторы предлагают подходы к согласованию прогнозов в масштабах миллиардов записей, что фактически признает неизбежность расхождений и необходимость их адаптивного смягчения. Это созвучно убеждению, что контроль — это иллюзия, требующая SLA. Бертранд Рассел однажды заметил: «Всё, что построено, когда-нибудь начнёт само себя чинить». Данная работа, рассматривая оптимизацию иерархического прогнозирования, словно подтверждает эту мысль: системы, подобные тем, что описаны в статье, не проектируются как статичные конструкции, а развиваются, самокорректируясь в процессе эксплуатации и адаптации к изменяющимся условиям.

Что дальше?

Представленные алгоритмы примирения прогнозов, несомненно, расширяют границы возможного в обработке колоссальных объёмов данных. Однако, за кажущейся точностью скрывается старая истина: система, способная предсказать всё, лишена места для неожиданности, а значит, и для жизни. Решение, идеально согласующее миллиарды прогнозов, оказывается стерильным, лишённым той творческой неразберихи, которая и является сутью реальных рынков.

Следующий этап развития, вероятно, связан не с усложнением математических моделей, а с принятием неизбежной неточности. Вместо погони за абсолютной согласованностью, стоит обратить внимание на способы извлечения ценности из расхождений. Ведь именно в отклонениях от прогноза кроется информация о новых трендах, о непредсказуемых изменениях в поведении потребителей.

Более того, представленный подход, хоть и масштабируем, всё ещё опирается на предположение о стационарности базовых связей. Настоящий вызов — разработка алгоритмов, способных адаптироваться к постоянно меняющейся структуре данных, к появлению новых уровней иерархии. Система, которая никогда не ломается, мертва. И в этом её парадоксальная сила.

Оригинал статьи: https://arxiv.org/pdf/2602.05030.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-07 18:50