Карты вознаграждений: Новый подход к обучению генеративных моделей

Автор: Денис Аветисян

В статье представлен инновационный метод, позволяющий эффективно согласовывать цели генеративных моделей с желаемым поведением, используя стохастические карты потока.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Карты алмазных потоков представляют собой стохастические карты потоков, позволяющие выполнять одношаговые «прогнозы» траектории потока к потенциальным конечным точкам, что обеспечивает эффективное исследование, поиск и навигацию, при этом предложены два варианта реализации: карты апостериорных потоков, дистиллирующие потоки GLASS в карту потоков [latex]X\_{s,r}(\bar{x}|x\_{t},t)[/latex] для точной выборки из апостериорного распределения, и взвешенные карты алмазных потоков, позволяющие использовать стандартные карты потоков посредством простого добавления шума, что повышает эффективность выборки (ESS) и улучшает выравнивание изображений, как демонстрируется на примерах запросов, включающих — Карты алмазных потоков представляют собой стохастические карты потоков, позволяющие выполнять одношаговые «прогнозы» траектории потока к потенциальным конечным точкам, что обеспечивает эффективное исследование, поиск и навигацию, при этом предложены два варианта реализации: карты апостериорных потоков, дистиллирующие потоки GLASS в карту потоков $X\_{s,r}(\bar{x}|x\_{t},t)$ для точной выборки из апостериорного распределения, и взвешенные карты алмазных потоков, позволяющие использовать стандартные карты потоков посредством простого добавления шума, что повышает эффективность выборки (ESS) и улучшает выравнивание изображений, как демонстрируется на примерах запросов, включающих «алмаз, сложенную карту сокровищ, компас и кинжал» и «ноутбук на плюшевом мишке».

Исследование предлагает ‘Diamond Maps’ — технику оценки функции ценности и быстрого выравнивания вознаграждений для диффузионных моделей, превосходящую существующие методы.

Современные генеративные модели, такие как диффузионные, демонстрируют впечатляющие результаты, однако адаптация к предпочтениям пользователя после обучения остается сложной задачей. В работе ‘Diamond Maps: Efficient Reward Alignment via Stochastic Flow Maps’ предложен новый подход, основанный на стохастических картах потока, позволяющий эффективно оценивать функцию ценности и быстро согласовывать генеративные модели с заданными наградами. Ключевое преимущество ‘Diamond Maps’ заключается в амортизации множества шагов симуляции в единый шаг, сохраняя при этом необходимую стохастичность для оптимального выравнивания. Смогут ли эти методы открыть путь к созданию генеративных моделей, способных к быстрой адаптации к произвольным предпочтениям и ограничениям на этапе инференса?

Математическая Элегантность Генеративных Моделей

Современное генеративное моделирование опирается на способность алгоритмов изучать сложные распределения данных, что позволяет создавать реалистичные образцы, неотличимые от реальных. Вместо явного программирования правил создания данных, модели учатся выявлять закономерности в существующем наборе данных и воспроизводить их. Это достигается путем построения вероятностной модели, описывающей вероятность появления различных значений в данных. Например, модель может научиться, что определенные комбинации пикселей чаще встречаются в изображениях лиц, и использовать эту информацию для генерации новых, правдоподобных лиц. Изучение этих распределений позволяет создавать не просто копии существующих данных, но и генерировать новые, уникальные образцы, расширяя возможности в областях от компьютерной графики до разработки лекарств. $P(x)$ — функция плотности вероятности, описывающая распределение данных, и ее точное моделирование является ключевой задачей в генеративном моделировании.

Диффузионные модели и сопоставление потоков представляют собой передовые подходы в генеративном моделировании, объединяемые общей концепцией — преобразованием случайного шума в структурированные данные посредством последовательных вероятностных переходов. В основе этих методов лежит идея построения условных вероятностных путей, описывающих постепенное «упорядочение» случайного шума. Диффузионные модели достигают этого, добавляя шум к данным до тех пор, пока они не превратятся в чисто случайный сигнал, а затем обучая нейронную сеть «обращать» этот процесс, восстанавливая данные из шума. Сопоставление потоков, в свою очередь, стремится напрямую моделировать эти вероятностные пути, создавая непрерывные преобразования между шумом и данными, что позволяет более эффективно генерировать новые образцы. Оба подхода, несмотря на различия в реализации, демонстрируют впечатляющие результаты в создании реалистичных изображений, аудио и других типов данных, открывая новые горизонты в области искусственного интеллекта и машинного обучения.

Эффективное моделирование и выборка из сложных распределений данных является критически важным аспектом современных генеративных моделей. Несмотря на прогресс в архитектурах, таких как диффузионные модели и сопоставление потоков, практическая реализация этих методов требует инновационных подходов к оптимизации процесса выборки. Традиционные методы Монте-Карло часто оказываются вычислительно затратными, особенно в высокоразмерных пространствах данных. Поэтому, активно исследуются детерминированные методы, такие как нормальные потоки, и стохастические методы с уменьшенной дисперсией, направленные на ускорение сходимости и повышение эффективности. Разработка алгоритмов, способных быстро и точно генерировать реалистичные образцы из изученного распределения $p(x)$ , остается центральной задачей, определяющей возможности генеративных моделей в различных приложениях, от создания изображений до разработки новых материалов.

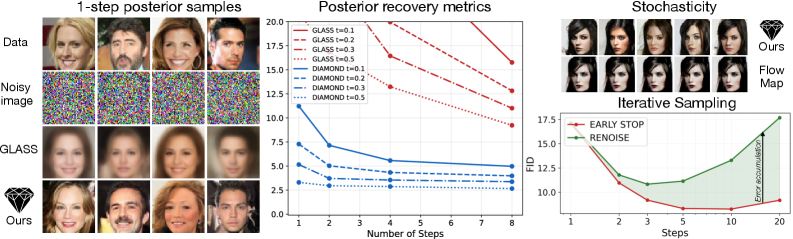
Карты апостериорных бриллиантов демонстрируют превосходство над потоковыми моделями при генерации высококачественных и разнообразных выборок будущего, обеспечивая возможность исследования различных сценариев и снижая накопление ошибок за счет итеративной схемы шумоподавления и добавления шума.

Согласование Вознаграждений: Эффективность Выборки

Настройка вознаграждения (Reward Alignment) представляет собой процесс, направленный на управление генеративными моделями для максимизации заданной функции вознаграждения. Это достигается путем обучения модели генерировать выходные данные, которые получают высокие оценки в соответствии с определенными критериями, заданными функцией вознаграждения. По сути, цель состоит в том, чтобы согласовать поведение модели с желаемыми целями, определяемыми этой функцией, что позволяет использовать генеративные модели для решения задач, требующих оптимизации по конкретным показателям. Определение функции вознаграждения является критически важным шагом, поскольку она напрямую влияет на поведение и результаты модели.

Процесс выравнивания вознаграждения (Reward Alignment) в значительной степени опирается на оценку ожидаемого вознаграждения, которое количественно определяется функцией ценности (Value Function). Функция ценности представляет собой предсказание о совокупном вознаграждении, которое система может получить, начиная с определенного состояния и действуя в соответствии с определенной политикой. Точная оценка этой функции критически важна для эффективного обучения модели генерации, поскольку позволяет оптимизировать ее поведение для достижения желаемых результатов. $V(s) = \mathbb{E}_{\tau \sim \pi}[R(\tau)]$ , где $V(s)$ — функция ценности в состоянии s, π — политика, а $R(\tau)$ — совокупное вознаграждение за траекторию τ.

Традиционные методы оценки ожидаемой награды в обучении с подкреплением, такие как Monte Carlo Tree Search (MCTS) или методы на основе Policy Gradient, часто требуют значительных вычислительных ресурсов, особенно в задачах с высокой размерностью пространства состояний или действий. Это обусловлено необходимостью большого количества симуляций или взаимодействий со средой для получения статистически значимой оценки. В связи с этим, разработка эффективных одношаговых семплеров является актуальной задачей. Наш подход демонстрирует повышенную эффективность использования данных (sample efficiency) по сравнению с базовыми моделями, что позволяет достичь сопоставимых результатов при значительно меньшем количестве итераций обучения и, следовательно, снизить общую вычислительную стоимость.

Результаты демонстрируют качественное соответствие между наградой CLIP и результатами, полученными с помощью Sequential Monte Carlo с Posterior Diamond Maps, при обучении модели на датасете CelebA.

Алмазные Карты: Стохастические Потоки для Максимизации Вознаграждений

Карты алмазов (Diamond Maps) представляют собой стохастические потоковые отображения, разработанные для эффективного преобразования случайного шума в данные, что позволяет оптимизировать соответствие между моделью и целевой функцией вознаграждения. В основе данного подхода лежит идея использования непрерывных преобразований вероятностного пространства, обеспечивающих плавный переход от случайного входа к целевым данным. Эффективность достигается за счет структурированной организации потока, позволяющей минимизировать потери информации и обеспечивать высокую точность сопоставления, что критически важно для задач обучения с подкреплением и оптимизации функций вознаграждения. В отличие от традиционных методов, карты алмазов позволяют эффективно исследовать пространство состояний и находить оптимальные стратегии поведения агента.

Постериорные и взвешенные алмазные карты (Posterior Diamond Maps и Weighted Diamond Maps) усовершенствуют базовый подход за счет интеграции методов последовательного Монте-Карло (Sequential Monte Carlo, SMC) и использования стохастичности. Применение SMC позволяет более эффективно оценивать апостериорное распределение, улучшая точность оценки ценности и снижая дисперсию. Введение стохастичности в процесс отображения способствует исследованию большего пространства состояний и повышает устойчивость алгоритма к шуму, что особенно важно при решении сложных задач оптимизации и анализе Парето-фронта. Эти методы позволяют получать более надежные и точные оценки ценности, необходимые для принятия оптимальных решений в условиях неопределенности.

Методы, использующие переходы диффузионных вероятностных моделей (DDPM) и стохастические потоки, позволяют проводить быструю и точную оценку функции ценности. Применение DDPM-переходов обеспечивает эффективное моделирование вероятностных распределений, необходимое для оценки ценности состояний. Стохастические потоки, в свою очередь, оптимизируют процесс сэмплирования и ускоряют сходимость алгоритмов. В результате достигается высокая точность в оценке функции ценности, что, в свою очередь, приводит к улучшению результатов при анализе Парето-фронта, позволяя более эффективно находить оптимальные решения в многокритериальных задачах.

Использование взвешенных карт ромбов обеспечивает значительно более эффективное масштабирование по сравнению с методом Best-of-N при планировании траектории, как показано на парето-фронте, полученном с увеличением количества шагов планирования до [latex]N=4[/latex] при использовании метода Монте-Карло. — Использование взвешенных карт ромбов обеспечивает значительно более эффективное масштабирование по сравнению с методом Best-of-N при планировании траектории, как показано на парето-фронте, полученном с увеличением количества шагов планирования до $N=4$ при использовании метода Монте-Карло.

Влияние и Перспективы Дальнейших Исследований

Карты Алмазов значительно повышают эффективность обучения и работы генеративных моделей за счет быстрого и точного выравнивания системы вознаграждений. Традиционно, процесс обучения таких моделей требует значительных вычислительных ресурсов и времени, поскольку необходимо тщательно настроить параметры, чтобы сгенерированные результаты соответствовали желаемым критериям. Новая методика позволяет модели быстро «находить» оптимальные стратегии, максимизирующие вознаграждение, что приводит к сокращению времени обучения и снижению затрат на ресурсы. Более того, точное выравнивание вознаграждений обеспечивает более предсказуемые и качественные результаты, что критически важно для приложений, требующих высокой степени контроля над генерируемым контентом, таких как создание персонализированных рекомендаций или моделирование сложных систем.

Возможность точного контроля над генерируемым контентом, обеспечиваемая данной технологией, открывает широкие перспективы для создания персонализированных пользовательских опытов. Например, в сфере развлечений это позволяет создавать интерактивные истории, адаптирующиеся к предпочтениям каждого зрителя, или генерировать уникальные музыкальные композиции, соответствующие индивидуальному вкусу. Кроме того, технология находит применение в целевых симуляциях, где требуется моделирование сложных сценариев с высокой степенью детализации и точности, например, в обучении автономных систем или прогнозировании поведения в различных условиях. Благодаря возможности настраивать параметры генерации, становится возможным создание контента, идеально соответствующего конкретным потребностям и задачам, что значительно расширяет область применения генеративных моделей.

Дальнейшие исследования направлены на расширение возможностей предложенного подхода для работы с более сложными функциями вознаграждения, включающими нелинейные зависимости и многокритериальные оценки. Особое внимание будет уделено масштабируемости методов Diamond Maps для обработки данных высокой размерности, что критически важно для применения в реальных задачах, таких как генерация изображений высокого разрешения или моделирование сложных физических процессов. Разработка алгоритмов, эффективно работающих с многомерными пространствами признаков, позволит существенно повысить точность и реалистичность генерируемого контента, открывая новые перспективы для персонализированных приложений и продвинутых симуляций.

Исследование, представленное в статье, демонстрирует стремление к математической чистоте в области генеративных моделей. Авторы предлагают метод ‘Diamond Maps’, направленный на эффективную оценку функций ценности и быстрое выравнивание наград. Этот подход, как и любое элегантное решение, требует доказательства корректности, а не просто успешного прохождения тестов. Как однажды заметил Пол Эрдёш: «Математика — это алфавит, которым написана книга природы». Эта фраза отражает суть работы: стремление к точности и ясности в определении алгоритмов, чтобы обеспечить надежность и предсказуемость результатов, особенно в контексте сложных систем, таких как диффузионные модели и обучение с подкреплением. Минимизация избыточности и упрощение абстракций — ключевые принципы, определяющие ценность предложенного метода.

Что Дальше?

Представленные методы стохастических потоков, в частности, “Diamond Maps”, демонстрируют несомненный прогресс в задаче согласования вознаграждений для генеративных моделей. Однако, стоит помнить, что элегантность алгоритма не измеряется скоростью сходимости на тестовых данных, а строгостью математического доказательства его корректности. Очевидным направлением дальнейших исследований является формализация гарантий сходимости и устойчивости предложенных методов, а не просто эмпирическая демонстрация их эффективности.

Оптимизация без анализа — это самообман и ловушка для неосторожного разработчика. Следует признать, что текущие подходы к формированию вознаграждений часто носят эвристический характер. Настоящий прогресс потребует разработки методов, позволяющих автоматически выводить функции вознаграждения из формальных спецификаций, а не полагаться на интуицию и ручную настройку. Вопрос о масштабируемости этих методов на сложные, многомерные пространства остается открытым.

В конечном счете, задача согласования вознаграждений — это не просто техническая проблема, а философский вызов. Определение “правильного” вознаграждения требует глубокого понимания желаемого поведения модели и потенциальных побочных эффектов. До тех пор, пока эта проблема не будет решена, любые улучшения в скорости и эффективности будут лишь косметическими.

Оригинал статьи: https://arxiv.org/pdf/2602.05993.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-07 23:55