Рой под контролем: Безопасность и стабильность в больших системах

Автор: Денис Аветисян

Новый подход к управлению роем роботов гарантирует соблюдение ограничений безопасности и стабильности благодаря интеграции макроскопических ограничений и децентрализованных алгоритмов управления.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Наблюдается эволюция энтропии как в неконструированном, так и в случае с ограничением по CBF, при этом порог энтропии установлен на уровне [latex]\epsilon = 3[/latex], что демонстрирует динамику изменения неопределённости системы в зависимости от наложенных ограничений. — Наблюдается эволюция энтропии как в неконструированном, так и в случае с ограничением по CBF, при этом порог энтропии установлен на уровне $\epsilon = 3$ , что демонстрирует динамику изменения неопределённости системы в зависимости от наложенных ограничений.

В работе представлена методика, использующая Банаховы функции управления барьерами и оптимальный транспорт для обеспечения безопасности в крупномасштабных роевых системах.

Обеспечение безопасности и стабильности в системах, состоящих из большого числа взаимодействующих агентов, представляет собой сложную задачу, особенно при наличии макроскопических ограничений. В данной работе, ‘Banach Control Barrier Functions for Large-Scale Swarm Control’, предлагается новый подход, использующий банаховы функции управления барьерами для обеспечения безопасного управления роем агентов, моделируя его как вероятностное распределение в пространстве. Разработанный фреймворк позволяет интегрировать макроскопические ограничения безопасности с децентрализованными алгоритмами управления, основанными на алгоритмах оптимального транспорта, и выводить микроскопические алгоритмы, согласованные с макроскопическим поведением. Какие перспективы открывает предложенный подход для создания устойчивых и безопасных роевых систем в различных областях применения?

Понимание Сложности Многоагентных Систем

Традиционные подходы к обеспечению безопасности, разработанные для одиночных роботов или небольших групп, оказываются недостаточными при работе с многоагентными системами, состоящими из большого количества взаимодействующих сущностей. Сложность заключается в экспоненциальном росте количества возможных взаимодействий и сценариев, возникающих в динамичной среде. Прогнозирование и предотвращение столкновений, обеспечение согласованного поведения и избежание нежелательных последствий становятся чрезвычайно трудными задачами, требующими принципиально новых методов планирования и контроля. Ограничение действий каждого агента в отдельности, даже при строгом соблюдении заданных правил, не гарантирует общей безопасности системы, поскольку коллективное поведение может привести к возникновению непредсказуемых и опасных ситуаций.

Обеспечение коллективной безопасности в многоагентных системах требует принципиально иного подхода, чем просто наложение ограничений на действия каждого отдельного агента. Исследования показывают, что критически важным фактором является учет общей плотности распределения роя — то есть, как агенты расположены относительно друг друга в пространстве. Когда плотность агентов увеличивается в определенных областях, возрастает вероятность возникновения коллизий или нежелательных взаимодействий, даже если каждый агент действует в рамках заданных ограничений. Таким образом, эффективные стратегии обеспечения безопасности должны учитывать не только индивидуальное поведение, но и динамику всей популяции, адаптируясь к изменениям в ее плотности и распределении для предотвращения возникновения опасных ситуаций.

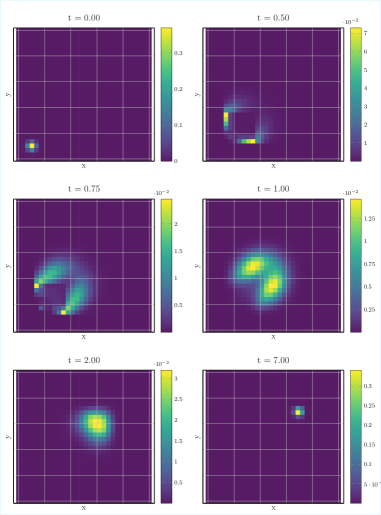
Тепловая карта демонстрирует эволюцию плотности при обходе препятствия в 2D, показывая успешное перераспределение плотности от начального к целевому состоянию с обходом опасной зоны, определяемой квадратом.

Управление Плотностью: Новый Подход к Координации

Управление плотностью (Density Steering) представляет собой методологию для эволюции распределения агентов из начального состояния в целевое, с обязательным соблюдением ограничений безопасности. Данный подход позволяет динамически изменять плотность агентов в пространстве, гарантируя, что траектории их движения не нарушают заданные границы и правила. Это достигается путем определения желаемого конечного распределения и последующего формирования управляющих воздействий, которые постепенно трансформируют исходное распределение в целевое, избегая столкновений или выхода за пределы допустимых областей. Методика применима в задачах координации множества агентов, таких как робототехника, моделирование поведения толпы и планирование траекторий в сложных средах.

Управление плотностью достигается за счет использования оптимального транспорта для определения траекторий распределения плотности агентов. Оптимальный транспорт, как математический инструмент, позволяет найти наиболее эффективный способ перемещения начального распределения вероятностей в целевое, минимизируя «стоимость» перемещения. В контексте управления роем, это означает определение пути эволюции плотности агентов в пространстве состояний таким образом, чтобы минимизировать отклонения от желаемой конфигурации при соблюдении ограничений безопасности. $c(x,y)$ обозначает стоимость перемещения массы из точки $x$ в точку $y$ , а задача оптимального транспорта формулируется как минимизация интеграла $\in t c(x,y) d\mu(x,y)$ при заданных начальном и целевом распределениях $\mu_0$ и $\mu_1$ соответственно.

Для обеспечения плавного изменения распределения плотности агентов во времени, в Density Steering используются градиентные потоки. Эти потоки позволяют сформулировать законы управления, основанные на вычислении градиента функционала, описывающего желаемое состояние плотности. В частности, производная по времени от функции плотности $\rho(x,t)$ определяется как $\frac{\partial \rho}{\partial t} = \nabla_x \cdot ( \rho \nabla_x V(x) )$ , где $V(x)$ представляет собой потенциал, определяющий направление эволюции плотности к целевому состоянию. Использование градиентных потоков гарантирует монотонное уменьшение функционала и, следовательно, устойчивое приближение к желаемой плотности при соблюдении заданных ограничений безопасности.

Ограничение функции Колмогорова-Баранова (CBF) обеспечивает распределение агентов, соответствующее целевой плотности, избегая нарушений максимальной плотности [latex]\varepsilon_{max} = 0.045[/latex] и поддерживая минимальную плотность [latex]\varepsilon_{min} = 0.01[/latex], в отличие от неконтролируемого распределения. — Ограничение функции Колмогорова-Баранова (CBF) обеспечивает распределение агентов, соответствующее целевой плотности, избегая нарушений максимальной плотности $\varepsilon_{max} = 0.045$ и поддерживая минимальную плотность $\varepsilon_{min} = 0.01$ , в отличие от неконтролируемого распределения.

Функции Банахова Барьера Управления: Повышение Надёжности в Сложных Системах

Традиционные функции барьерного управления (Control Barrier Functions, CBF) часто оказываются недостаточными для обеспечения безопасности в сложных многоагентных системах, характеризующихся стохастическими возмущениями и пространственной зависимостью ограничений. Для решения этой проблемы предложено расширение в виде Функций Банахова Барьера Управления (Banach Control Barrier Functions, B-CBF). B-CBF используют функциональные пространства Банаха для представления ограничений безопасности, что позволяет учитывать неопределенности и пространственные зависимости, не требуя явного моделирования этих факторов. Это расширение позволяет эффективно кодировать требования безопасности, такие как предотвращение столкновений и поддержание когерентности роя, непосредственно в процесс разработки управления, обеспечивая более надежное и устойчивое поведение системы в сложных условиях.

Функции барьерного управления Банаха (B-CBF) позволяют напрямую включать требования безопасности, такие как предотвращение столкновений, поддержание связности роя и обеспечение нижних границ энтропии, непосредственно в процесс проектирования системы управления. В отличие от традиционных функций барьерного управления, B-CBF оперируют с функциями, определенными в банаховых пространствах, что позволяет эффективно учитывать пространственную зависимость и неопределенности, характерные для многоагентных систем. Это достигается путем формулирования ограничений безопасности как неравенств, включающих состояние системы и управляющие воздействия, что позволяет при разработке стратегии управления учитывать эти ограничения и гарантировать их выполнение. $h(x) \geq 0$ означает, что состояние системы $x$ остается в безопасной области, определяемой функцией $h$ .

Интеграция функций безопасности Банаха (B-CBF) с методом управления плотностью (density steering) обеспечивает сходимость системы к безопасным областям и поддержание ограничений безопасности. Данный подход позволяет гарантировать, что траектория системы останется в пределах заданных безопасных границ, даже при наличии неопределенностей и возмущений. Эффективность предложенного метода была подтверждена посредством численного моделирования, демонстрирующего его способность поддерживать желаемые свойства безопасности в различных сценариях. В частности, симуляции показали устойчивое выполнение ограничений безопасности, заданных с помощью B-CBF, в условиях динамического окружения и при взаимодействии с другими агентами.

Кривые, показывающие начальную и конечную плотности ([latex]\rho_{0}, \rho_{*}\[/latex]), выделяют небезопасную область, в то время как эволюция плотности без ограничений (красный) и после CBF-проекции (синий) демонстрирует обеспечение безопасности. — Кривые, показывающие начальную и конечную плотности ( $\rho_{0}, \rho_{*}\$ ), выделяют небезопасную область, в то время как эволюция плотности без ограничений (красный) и после CBF-проекции (синий) демонстрирует обеспечение безопасности.

Распределённая Реализация и Производительность Системы

В основе предлагаемого подхода лежит микроскопическая реализация, предполагающая распределение законов управления непосредственно между отдельными агентами роя. Вместо централизованного контроля, каждый агент действует автономно, опираясь на локальные правила и информацию, что значительно повышает устойчивость и масштабируемость системы. Такой принцип позволяет избежать «узких мест», возникающих при централизованной обработке данных, и обеспечивает более быстрое и эффективное реагирование на изменения в окружающей среде. Каждый агент, действуя по своим локальным правилам, вносит вклад в общее поведение роя, формируя сложные и скоординированные действия без необходимости глобальной координации. Это особенно важно в динамичных и непредсказуемых средах, где быстрота и адаптивность являются ключевыми факторами успеха.

Основой для реализации распределенного управления является разбиение пространства на диаграммы Вороного, где каждому агенту присваивается уникальная область влияния. Данный подход позволяет каждому агенту принимать решения, основываясь исключительно на информации, полученной из его непосредственного окружения, что значительно снижает вычислительную сложность и повышает масштабируемость системы. В рамках каждой ячейки Вороного агент самостоятельно регулирует свои параметры, стремясь к достижению глобальной цели без необходимости централизованного управления или обмена данными со всеми другими агентами. Такое локализованное принятие решений обеспечивает устойчивость системы к отказам отдельных агентов и позволяет эффективно адаптироваться к изменениям в окружающей среде, поскольку каждый агент реагирует на локальные возмущения, а не ждет команд сверху.

В рамках распределенной системы управления роем агентов, для оценки различий между вероятностными распределениями, описывающими состояние каждого агента, применяется расстояние Вассерштейна. В отличие от евклидова расстояния, которое чувствительно к выбросам и требует определения соответствия между точками, расстояние Вассерштейна, также известное как расстояние Землеройки $\mathcal{W}(P, Q)$ , определяет минимальную «стоимость» перемещения массы вероятности из распределения $P$ в распределение $Q$ . Это делает его особенно устойчивым к шумам и неточностям в данных, а также позволяет эффективно оценивать сходство между распределениями даже при их значительном разбросе. Использование расстояния Вассерштейна в алгоритме управления обеспечивает надежную координацию агентов, позволяя им поддерживать желаемое поведение роя, несмотря на неопределенности и помехи в окружающей среде.

В ходе проведенного моделирования продемонстрирована способность системы поддерживать уровень энтропии выше заданного порогового значения на протяжении всего периода симуляции. Этот показатель является ключевым для обеспечения стабильного поведения роя, предотвращая коллапс в единую точку или непредсказуемое рассеяние. Поддержание достаточной энтропии способствует сохранению разнообразия в движениях агентов, позволяя рою эффективно исследовать пространство и адаптироваться к изменяющимся условиям. Исследования показали, что даже при наличии внешних возмущений или изменениях в окружающей среде, разработанный алгоритм контроля позволяет рою сохранять когерентность и функциональность, что подтверждает его надежность и эффективность в задачах коллективного поведения.

Исследование, представленное в данной работе, акцентирует внимание на необходимости обеспечения безопасности и стабильности в сложных роевых системах. Подход, основанный на использовании функций безопасности Банаха и оптимального транспорта, позволяет объединить глобальные ограничения безопасности с децентрализованными алгоритмами управления. Этот метод особенно важен для масштабируемых систем, где централизованное управление становится непрактичным. Как однажды заметил Лев Ландау: «Теория — это корни, а практика — плоды». В контексте роевой робототехники, строгое математическое обоснование, представленное в статье, служит тем самым корнем, необходимым для реализации надежных и безопасных алгоритмов управления, а практическая реализация — плодами, которые могут изменить принципы координации в сложных системах.

Куда дальше?

Представленная работа, безусловно, расширяет границы применения Control Barrier Functions к крупномасштабным роевым системам. Однако, стоит признать, что строгость математической модели, хоть и обеспечивает гарантии безопасности, одновременно накладывает ограничения на практическую реализацию. Вопрос о влиянии шумов, неизбежно присутствующих в реальных системах, и о робастности предложенного подхода к этим возмущениям остаётся открытым. Необходимо дальнейшее исследование, направленное на разработку адаптивных механизмов, способных компенсировать неопределённости и обеспечить устойчивость системы в условиях неидеальной информации.

Интересным направлением представляется интеграция предложенного фреймворка с алгоритмами обучения с подкреплением. Возможность динамической корректировки Control Barrier Functions на основе опыта, полученного в процессе взаимодействия с окружающей средой, может значительно повысить гибкость и эффективность управления роем. Впрочем, здесь возникает классический парадокс: насколько можно «обучать» систему, гарантируя при этом её безопасность? Граница между адаптацией и непредсказуемостью требует тщательного изучения.

Наконец, нельзя игнорировать вопрос масштабируемости. Хотя работа демонстрирует перспективность подхода к крупномасштабным системам, реальные рои могут содержать тысячи или даже миллионы агентов. Эффективное распределение вычислительной нагрузки и обеспечение своевременной коммуникации между агентами становятся критически важными задачами. По сути, предложенный фреймворк — это лишь первый шаг на пути к созданию действительно интеллектуальных и безопасных роевых систем.

Оригинал статьи: https://arxiv.org/pdf/2602.05011.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-08 18:27