Турниры и рейтинги: новый подход к поиску лучших

Автор: Денис Аветисян

Исследователи предлагают принципиально новый метод определения наиболее значимых элементов в наборе данных, используя концепцию турнирных графов.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал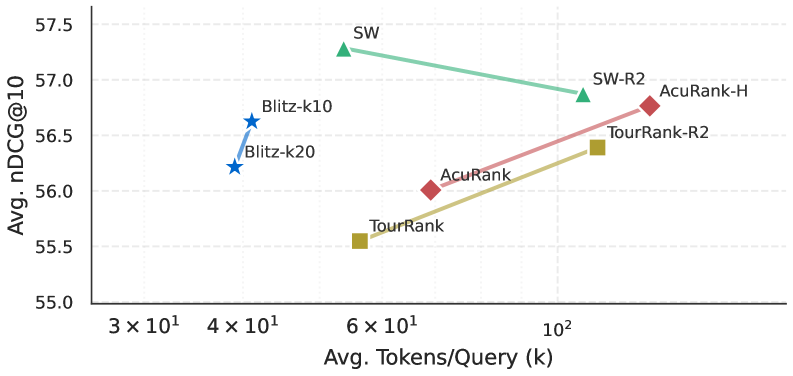

Алгоритм BlitzRank последовательно демонстрирует превосходство в достижении высокой точности при одновременном значительном снижении количества используемых токенов (на 25-40%) по сравнению с методами сопоставимой структуры, что подтверждает его эффективность в оптимизации соотношения точности и вычислительных затрат.

Предложенная схема обеспечивает теоретические гарантии и демонстрирует высокую эффективность даже при наличии противоречивых или циклических предпочтений.

Несмотря на впечатляющие возможности больших языковых моделей в качестве переранжировщиков, существующие подходы часто неэффективно используют информацию, заключенную в каждом сравнении документов. В данной работе, ‘BLITZRANK: Principled Zero-shot Ranking Agents with Tournament Graphs’, предложен новый фреймворк, основанный на теории турнирных графов, для принципиального решения задачи выбора $m$ лучших элементов из заданного множества. Ключевым наблюдением является возможность агрегирования парных предпочтений, выявленных LLM, в глобальный граф предпочтений, транзитивное замыкание которого позволяет получить дополнительные сведения без дополнительных запросов к модели. Может ли предложенный алгоритм, основанный на жадном максимизировании информационного выигрыша, обеспечить оптимальную или близкую к оптимальной производительность даже при наличии не транзитивных предпочтений и циклических зависимостей в оценках LLM?

Задача Выбора Лучших Элементов: Основа Современных Систем

Задача выделения лучших m элементов из большего набора является основополагающей для широкого спектра приложений, простирающихся от систем рекомендаций до анализа данных. В системах, предлагающих фильмы или товары, алгоритм должен быстро и точно определить наиболее подходящие варианты для каждого пользователя. Аналогично, в задачах анализа данных, будь то выявление наиболее важных трендов или определение ключевых факторов, влияющих на определенное явление, необходимо эффективно отбирать наиболее значимые элементы из большого объема информации. Эта проблема возникает повсеместно, когда требуется сократить массив данных до наиболее релевантных и ценных компонентов, что делает её центральной для многих областей науки и техники. Эффективное решение этой задачи напрямую влияет на производительность и точность различных алгоритмов и систем, обеспечивая более быстрый и надежный доступ к необходимой информации.

Традиционные методы парного ранжирования, несмотря на свою концептуальную простоту, сталкиваются со значительными вычислительными трудностями при увеличении числа оцениваемых элементов. В основе этих методов лежит сравнение каждого элемента со всеми остальными, что требует $O(n^2)$ операций, где $n$ — количество элементов. По мере роста $n$ , вычислительная сложность экспоненциально возрастает, делая подобные подходы непрактичными для задач, включающих большие объемы данных, например, в рекомендательных системах с миллионами товаров или при анализе больших баз данных. Таким образом, поиск эффективных альтернатив парному ранжированию становится критически важной задачей для решения проблем, связанных с масштабируемостью и производительностью.

Существующие методы выбора лучших элементов из множества часто сталкиваются с проблемой непереходных предпочтений, что приводит к непоследовательным и даже логически неверным результатам. Представьте ситуацию, когда алгоритм рекомендует книгу A пользователю, затем книгу B вместо A, а затем снова книгу A вместо B — подобная цикличность демонстрирует неспособность системы сформировать стабильный и осмысленный рейтинг. Эта проблема особенно актуальна в сложных системах, где оценки формируются на основе множества факторов и взаимосвязей, и где прямое сравнение элементов может быть неоднозначным. Неспособность корректно обрабатывать непереходные предпочтения может приводить к снижению доверия пользователей к рекомендациям и ухудшению общей эффективности системы, требуя разработки более устойчивых и логически обоснованных алгоритмов.

Сравнительный анализ эффективности методов переранжировки списков на 14 наборах данных (GPT-4.1) показывает, что BlitzRank обеспечивает минимальное потребление токенов и требует в среднем около [latex]\sim6.5[/latex] вызовов LLM, значительно превосходя такие методы, как Sliding Window, TourRank и AcuRank, особенно на коротких документах, как в наборе данных NFCorpus. — Сравнительный анализ эффективности методов переранжировки списков на 14 наборах данных (GPT-4.1) показывает, что BlitzRank обеспечивает минимальное потребление токенов и требует в среднем около $\sim6.5$ вызовов LLM, значительно превосходя такие методы, как Sliding Window, TourRank и AcuRank, особенно на коротких документах, как в наборе данных NFCorpus.

Турнирные Графы: Новый Подход к Выбору Лучших

Задача выбора $m$ лучших элементов моделируется с использованием турнирного графа. В данном представлении каждый элемент рассматривается как вершина графа, а ребра направлены от элемента $i$ к элементу $j$ , если $i$ признается лучшим при сравнении с $j$ . Таким образом, каждое сравнение между двумя элементами соответствует одному ребру в графе, и полный турнирный граф, содержащий все возможные сравнения, позволяет представить все отношения между элементами в структурированном виде. Использование турнирных графов обеспечивает формальную основу для анализа и оптимизации процесса выбора лучших элементов, позволяя применять инструменты и алгоритмы теории графов.

В рамках данной системы используется KKWiseComparisonOracle, позволяющий проводить эффективные попарные сравнения множеств элементов. Вместо последовательного сравнения каждого элемента с каждым другим, оракул оптимизирует процесс, используя свойства сравнения множеств для снижения общего числа запросов. Это достигается за счет группового анализа и выявления доминирующих элементов в пределах групп, что позволяет исключить необходимость в отдельных сравнениях для заведомо уступающих элементов. В результате, количество необходимых запросов к оракулу значительно уменьшается, особенно при работе с большими объемами данных, что существенно повышает эффективность алгоритма отбора $m$ лучших элементов.

Представление элементов в виде узлов графа позволяет использовать свойства теории графов для оптимизации процесса отбора. В частности, структура турнирного графа, где каждое ребро указывает на предпочтение одного элемента над другим, предоставляет возможность применения алгоритмов поиска оптимальных путей и выявления доминирующих узлов. Это позволяет избежать необходимости попарных сравнений всех элементов, что существенно снижает вычислительную сложность задачи, особенно при большом количестве рассматриваемых объектов. Использование свойств, таких как транзитивность и циклы, позволяет эффективно отсеивать неоптимальные варианты и сосредоточиться на наиболее перспективных кандидатах, что повышает скорость и эффективность процесса отбора.

Экспериментальные данные о количестве запросов [latex]Q(n,k,m)[/latex] для различных конфигураций [latex](n,k)[/latex] демонстрируют, что теоретическая оценка [latex]B(n,k,m)[/latex] (оранжевый цвет) точно соответствует эмпирической сложности, а её 1.25-кратное увеличение (зеленый цвет) ограничивает все наблюдаемые значения. — Экспериментальные данные о количестве запросов $Q(n,k,m)$ для различных конфигураций $(n,k)$ демонстрируют, что теоретическая оценка $B(n,k,m)$ (оранжевый цвет) точно соответствует эмпирической сложности, а её 1.25-кратное увеличение (зеленый цвет) ограничивает все наблюдаемые значения.

Эффективная Финализация на Основе Анализа Графов

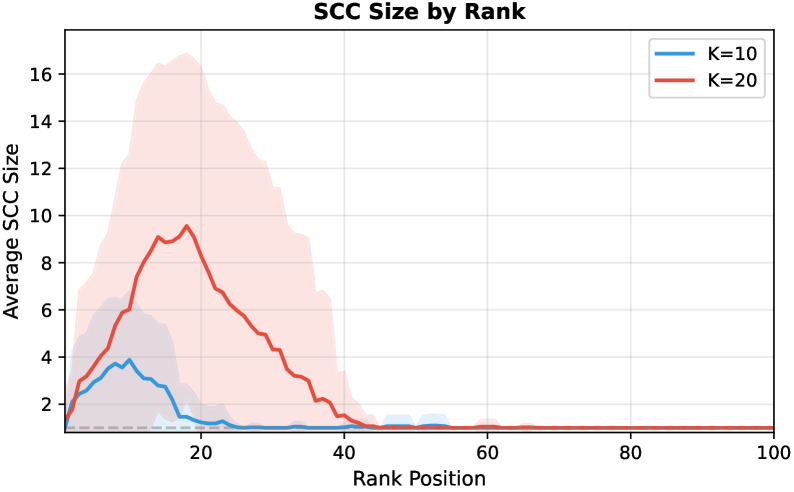
Критерий окончательной идентификации узлов (или сильно связных компонент) в топ-m основывается на понятиях ‘InReach’ и ‘LossCount’. ‘InReach’ определяет количество входящих связей от узлов, которые гарантированно находятся в топ-m, в то время как ‘LossCount’ фиксирует количество исходящих связей к узлам, которые не могут быть в топ-m. Узел (или SCC) считается окончательно идентифицированным, если его ‘InReach’ достаточно велик, чтобы гарантировать его принадлежность к топ-m, несмотря на потенциальные потери из-за исходящих связей к не-топовым узлам, определяемые ‘LossCount’. Эффективное вычисление этих метрик позволяет однозначно определить принадлежность узла к топ-m без необходимости полного сравнения с другими узлами.

Для снижения вычислительной сложности анализа при определении финального ранжирования, сильно связные компоненты (Strongly Connected Components, SCC) рассматриваются как единые узлы в конденсированном графе (CondensationGraph). Такой подход позволяет агрегировать взаимосвязанные узлы, уменьшая общее количество элементов, подлежащих анализу, без потери точности определения топ-m узлов. Вместо анализа каждого отдельного узла внутри SCC, анализируется только один представитель SCC в конденсированном графе, что существенно снижает потребность в ресурсах и ускоряет процесс вычисления. При этом, информация о взаимосвязях внутри SCC сохраняется в структуре конденсированного графа, обеспечивая корректность результатов.

Для оптимизации производительности и минимизации общего числа запросов используется жадный алгоритм (GreedyAlgorithm) при планировании последовательности запросов к графу. Асимптотическая сложность данного подхода составляет $O((n-1)/(k-1) + (m-1)/(k-1) * (1 + log_k(m)))$ , где n — количество узлов, m — количество сильно связных компонент (SCC), а k — параметр, определяющий размер подмножества лучших узлов. Эмпирические результаты подтверждают эффективность предложенного алгоритма в снижении QueryComplexity по сравнению с наивными подходами к определению топ-m узлов.

Анализ сильно связанных компонент после сходимости на DL19 с использованием GPT-4.1 показывает, что увеличение параметра k до 20 приводит к формированию более крупных компонент, сконцентрированных в рангах 10-40, в то время как k=10 способствует образованию меньших компонент в рангах 1-20, при этом средний размер компонент для обеих конфигураций демонстрирует волнообразный паттерн с пиками в средних рангах.

Влияние и Перспективы Развития

Предложенная методика значительно повышает эффективность отбора лучших m элементов, особенно в ситуациях, когда количество рассматриваемых объектов очень велико. Исследования показали, что использование данной системы позволяет снизить потребление токенов на 25-40% по сравнению с существующими подходами. Это достигается за счет оптимизации процесса оценки и отбора, что делает её особенно ценной в задачах, требующих обработки больших объемов данных и ограниченных вычислительных ресурсов. Такое снижение нагрузки позволяет ускорить работу систем и снизить затраты на их функционирование, открывая возможности для более широкого применения в различных областях, где требуется эффективный отбор из большого количества вариантов.

Работа продемонстрировала способность эффективно учитывать непереходные предпочтения, что значительно повышает надежность и устойчивость принимаемых решений. В ситуациях, когда выбор «А» предпочтительнее «Б», а «Б» предпочтительнее «В», но при этом «В» может оказаться более предпочтительным, чем «А», традиционные алгоритмы часто дают сбои. Данный подход позволяет корректно обрабатывать подобные парадоксы, обеспечивая более реалистичные и обоснованные результаты, особенно в сложных системах принятия решений, где важна целостность и логичность выбора. Это особенно критично для приложений, требующих последовательного и непротиворечивого выбора, гарантируя, что конечный результат будет соответствовать ожиданиям и потребностям пользователя.

Перспективы дальнейших исследований данной структуры простираются на разнообразные области применения. Особый интерес представляет возможность её использования в системах рекомендаций, где эффективный отбор наиболее подходящих вариантов играет ключевую роль. Кроме того, предложенный подход может быть успешно применён в задачах обнаружения аномалий, позволяя более точно выявлять отклонения от нормы в больших объемах данных. Не менее важным представляется потенциал в области распределения ресурсов, где оптимизация выбора и назначения ресурсов может значительно повысить эффективность и снизить издержки. В совокупности, эти направления открывают широкие возможности для практического внедрения и дальнейшего развития предложенной методологии.

В отличие от других наборов данных, где BM25 извлекает 100 документов на запрос, в NFCorpus наблюдается бимодальное распределение с преобладанием запросов, возвращающих менее 20 кандидатов (среднее: 68.2), что объясняет более низкое количество вызовов LLM, представленное в Таблице 4.

Представленная работа демонстрирует элегантность подхода к определению оптимальных решений в сложных системах, что перекликается с идеей о том, что структура определяет поведение. Авторы исследуют турнирные графы и алгоритмы выбора, показывая, как даже в условиях непоследовательности или циклических предпочтений можно достичь высокой эффективности. Как заметил Роберт Тарьян: «Простота — это высшая степень совершенства». Этот принцип находит отражение в предложенном фреймворке, стремящемся к минимизации сложности запросов и обеспечению теоретических гарантий производительности, особенно в контексте задачи выбора топ-m элементов. Эффективность алгоритма тесно связана с пониманием и упрощением структуры турнирных графов, что подчеркивает важность четкой и ясной организации системы.

Куда Далее?

Представленная работа, исследуя возможности ранжирования на основе турнирных графов, демонстрирует элегантность простого подхода к сложной задаче. Однако, истинная цена принятых решений проявляется лишь при столкновении с нелинейностью реальных данных. Эффективность жадного алгоритма, гарантированная в определенных условиях, все же требует осторожности при экстраполяции на случаи с сильно зашумленными или неполными предпочтениями. Вопрос о надежности конденсационных графов в качестве инструмента для снижения сложности запросов остается открытым, особенно при увеличении масштаба задачи.

Будущие исследования должны быть направлены на разработку методов адаптации к не-транзитивным турнирам без существенной потери производительности. Интересным направлением представляется изучение влияния структуры турнирного графа на эффективность различных стратегий запросов. Возможно, стоит переосмыслить критерии окончательной финализации, учитывая компромисс между точностью и стоимостью запросов, ведь стремление к идеальному ранжированию не всегда оправдано.

Хорошая архитектура незаметна, пока не ломается, и только тогда видна настоящая цена решений. Предложенный подход — это первый шаг к созданию устойчивых и эффективных систем ранжирования, но дальнейшее развитие требует глубокого понимания лежащих в основе принципов и готовности к признанию неизбежных ограничений.

Оригинал статьи: https://arxiv.org/pdf/2602.05448.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-08 23:41