Риск и выживание: Новая модель для оценки совместных аннуитетов

от

Автор: Денис Аветисян

Исследование предлагает инновационный подход к расчету стоимости финансовых инструментов, связанных с совместным долголетием, учитывающий взаимозависимость между участниками.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал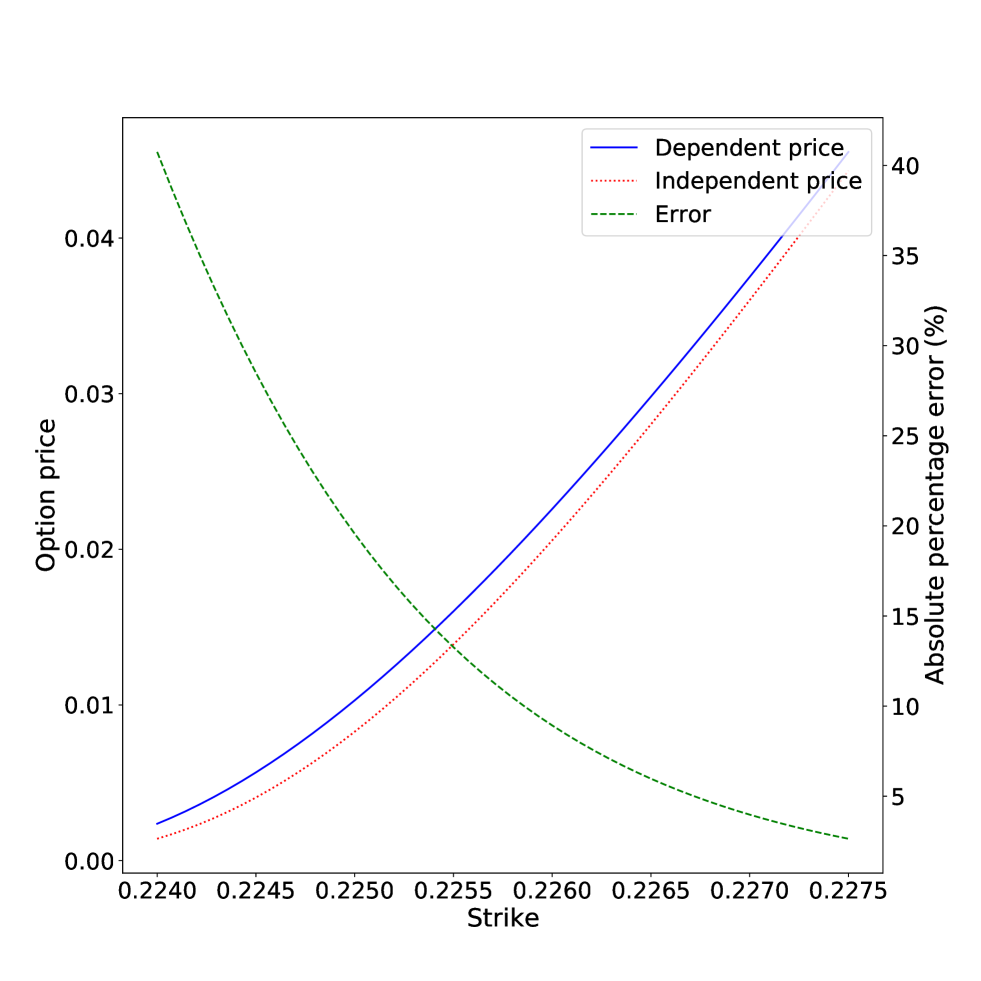
Разница в ценах, возникающая при допущении независимости и зависимости факторов, демонстрирует, что принятие более строгих, но менее реалистичных предположений может приводить к занижению оценок, в то время как учет взаимосвязей между переменными, хотя и сложнее, обеспечивает более точное и обоснованное ценообразование.
Разница в ценах, возникающая при допущении независимости и зависимости факторов, демонстрирует, что принятие более строгих, но менее реалистичных предположений может приводить к занижению оценок, в то время как учет взаимосвязей между переменными, хотя и сложнее, обеспечивает более точное и обоснованное ценообразование.

В статье представлена линейно-рациональная модель Вишарта для моделирования смертности и оценки производных инструментов, таких как совместные аннуитеты.

Оценка совместных аннуитетов и производных инструментов, учитывающих зависимость между жизнями застрахованных, представляет собой сложную задачу в актуарной науке. В данной работе, посвященной ‘Joint survival annuity derivative valuation in the linear-rational Wishart mortality model’, предложена новая модель, использующая процесс Уишарта в линейно-рациональном фреймворке для моделирования совместной смертности. Получены аналитические формулы для оценки аннуитетов и опционов, позволяющие учитывать сложные зависимости между интенсивностями смертности, а также разработаны приближенные методы для повышения скорости расчетов. Возможно ли дальнейшее развитие данной модели для учета более сложных факторов риска и улучшения управления портфелем актуарных инструментов?

Моделирование Совместной Судьбы: Вызовы Оценки Рисков

Оценка финансовых продуктов, зависящих от жизней нескольких застрахованных, представляет собой сложную задачу, выходящую за рамки возможностей стандартных актуарных методов. Традиционные модели, как правило, не способны адекватно отразить взаимосвязь между вероятностями наступления смерти у разных индивидуумов, что приводит к ошибкам в ценообразовании. Данная сложность обусловлена необходимостью учета не только индивидуальных рисков, но и их корреляции — вероятности одновременного наступления страховых случаев. Например, при страховании жизни супругов или партнеров по бизнесу, их судьбы тесно связаны, и игнорирование этой взаимосвязи может привести к значительным расхождениям в оценке стоимости страхового продукта. Применение стандартных актуарных моделей в таких случаях может приводить к занижению или завышению страховых премий, что делает их непригодными для адекватной оценки подобных финансовых инструментов.

Традиционные методы актуарного моделирования часто оказываются неспособны точно оценить сложные взаимосвязи между вероятностями смертности нескольких застрахованных лиц. Предположение об их независимости, упрощающее расчеты, может приводить к значительным ошибкам в ценообразовании финансовых продуктов, зависящих от жизней нескольких человек. Исследования показывают, что при допущении положительной зависимости между жизнями погрешность в оценке стоимости может достигать 40%, что подчеркивает необходимость разработки более сложных моделей, учитывающих корреляцию между индивидуальными рисками и обеспечивающих адекватное отражение реальной вероятности наступления страхового случая.

Основная сложность при моделировании финансовых продуктов, зависящих от жизни нескольких человек, заключается в адекватном представлении структуры взаимосвязей между их судьбами в рамках применимой математической модели. Недостаточно просто учесть индивидуальные вероятности наступления страхового случая; необходимо точно отразить, как смерть одного человека влияет на вероятность смерти других. Это требует разработки сложных статистических моделей, способных улавливать как положительные, так и отрицательные корреляции. Например, в случае супругов или деловых партнеров, существует вероятность положительной зависимости — смерть одного увеличивает риск для другого. Игнорирование этих взаимосвязей приводит к значительным ошибкам в оценке стоимости подобных финансовых продуктов, поскольку стандартные актуарные методы предполагают независимость рисков, что зачастую не соответствует действительности. Построение адекватной модели корреляции — это не только математическая, но и статистическая задача, требующая больших объемов данных и тщательного анализа.

Стохастическое Моделирование: Процесс Вишарта в Действии

Предлагаемая нами модельная структура использует процесс Уишарта для описания динамических зависимостей между индивидуальными интенсивностями смертности. Процесс Уишарта, являясь стохастическим процессом, действующим на положительно определенные матрицы, позволяет моделировать ковариационную структуру между жизнями, учитывая, что интенсивности смертности не являются независимыми. В рамках данной структуры, изменения в интенсивности смертности одного индивида влияют на вероятности смертности других, что особенно важно при оценке рисков, связанных с портфелем страховых полисов. Модель позволяет учитывать временные изменения в корреляциях между интенсивностями смертности, обеспечивая более реалистичное представление о динамике смертности в популяции.

Процесс Уишарта, являясь стохастическим процессом, оперирующим положительно определенными матрицами, обеспечивает естественное моделирование структуры корреляции между жизнями. В рамках данной модели, положительно определенная матрица ковариации Σ представляет взаимосвязи между интенсивностями смертности отдельных индивидуумов. Изменение этой матрицы во времени, описываемое процессом Уишарта, отражает динамические зависимости, позволяя учитывать влияние одновременных событий и общие факторы риска, влияющие на смертность группы лиц. Такая параметризация позволяет адекватно отобразить ковариационные связи, которые являются ключевыми для оценки рисков и формирования адекватных страховых тарифов.

Использование предложенной модели позволяет задать функцию плотности состояния (state-price density) — ключевой элемент в ценообразовании опционов — таким образом, чтобы она точно отражала взаимосвязи между интенсивностями смертности отдельных индивидуумов. Это достигается за счет использования стохастического процесса Вишарта, который по своей природе моделирует корреляционную структуру между жизнями. Такой подход обеспечивает возможность быстрой реализации модели в практических приложениях, поскольку функция плотности состояния определяется непосредственно через параметры процесса Вишарта, что упрощает калибровку и расчет опционных цен. S(t) = \exp(-X_t), где X_t — процесс Вишарта, описывающий динамику дисконтирующего фактора.

Аналитическая Точность: Линейная Рациональность и Замкнутые Решения

Ключевой особенностью представленной модели является её линейно-рациональная структура, позволяющая получить аналитические решения для оценки цены совместной аннуитетной выплаты. Данная структура предполагает, что цена аннуитета может быть выражена в виде рациональной функции от параметров модели, что делает возможным её прямое вычисление без необходимости использования численных методов или сложных симуляций. В частности, это означает, что цена аннуитета P может быть представлена как P = \frac{N(x, y)}{D(x, y)}, где N и D — полиномы от возрастов застрахованных x и y, а также других параметров, определяющих аннуитет.

Аналитическая разрешимость, обеспечиваемая данной моделью, представляет собой существенный прогресс в оценке совместных аннуитетов выживания. Вместо трудоемких численных методов и сложных симуляций, модель предоставляет формулы в замкнутой форме, позволяющие получить точные результаты непосредственно из заданных параметров. Это обеспечивает значительное повышение вычислительной эффективности и снижение затрат времени, особенно при проведении масштабных расчетов или анализе чувствительности. Использование аналитических выражений также устраняет погрешности, связанные с дискретизацией и аппроксимацией, характерными для численных методов, что повышает надежность и точность оценки стоимости аннуитета.

Процесс Вишарта напрямую обеспечивает вывод аналитических решений для оценки совместной аннуитетной выплаты. В частности, использование стохастической модели Вишарта позволяет получить замкнутые выражения для цены аннуитета, минуя необходимость в сложных численных симуляциях или итерационных процедурах. Это упрощает процесс оценки, снижает вычислительные затраты и повышает точность получаемых результатов, поскольку аналитические решения обеспечивают точное определение цены аннуитета без приближений, присущих методам моделирования. W_t — процесс Вишарта, который используется для моделирования динамики ковариационной матрицы базовых активов, что позволяет получить точные формулы для оценки.

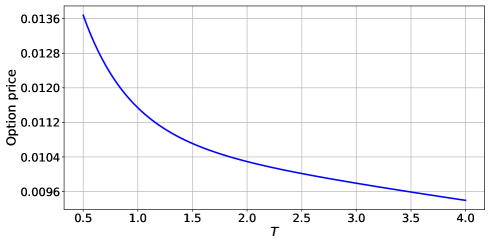
Анализ чувствительности выявил ключевые параметры, оказывающие наибольшее влияние на производительность системы.
Анализ чувствительности выявил ключевые параметры, оказывающие наибольшее влияние на производительность системы.

Улучшение Оценки с Использованием Численных Методов

В случаях, когда получение аналитического решения для оценки стоимости гарантированной аннуитетной опции совместного выживания становится невозможным, используются методы численного приближения. Эти методы позволяют оценить стоимость опции путём последовательного приближения к истинному значению, используя итеративные алгоритмы и дискретизацию исходной задачи. Невозможность получения аналитического решения обычно возникает из-за сложности математических выражений, описывающих вероятности выживания нескольких лиц, и интегралов, необходимых для расчета ожидаемых выплат. Численные методы предоставляют практический способ получения приемлемой оценки стоимости в таких ситуациях, хотя и с некоторой погрешностью.

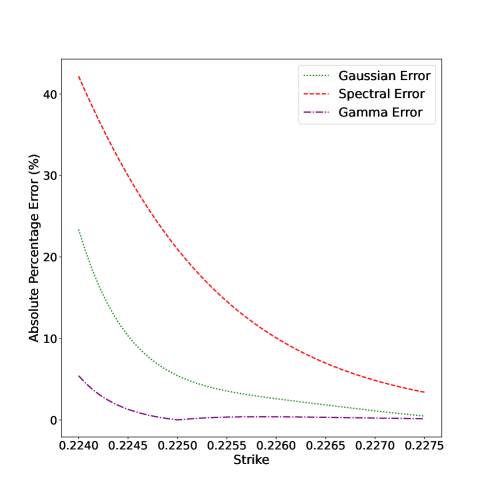
Для оценки стоимости гарантированной аннуитетной опции, при невозможности получения аналитических решений, применяются численные методы, такие как разложение по кумулянтам, спектральное разложение и аппроксимация гамма-распределением. Эти методы позволяют получить достаточно точные результаты с быстрой вычислительной реализацией. Разложение по кумулянтам использует моменты распределения для аппроксимации функции цены, в то время как спектральное разложение применяет разложение на собственные векторы для упрощения вычислений. Аппроксимация гамма-распределением использует гамма-распределение для моделирования вероятностей выживания и оценки опциона. Быстрая скорость вычислений делает их пригодными для оценки сложных контрактов с участием нескольких жизней и для реализации в реальном времени.

Комбинация аналитических и численных методов обеспечивает всестороннюю и надежную систему оценки сложных коллективных договоров страхования жизни. Аналитические решения, где это возможно, предоставляют точные базовые результаты и понимание ключевых факторов, влияющих на стоимость. Однако, при оценке контрактов, включающих большое количество участников или сложные зависимости между жизнями, аналитические решения становятся непрактичными. В таких случаях, численные методы, такие как разложение по кумулянтам, спектральное разложение и аппроксимация гамма-распределением, позволяют получить достаточно точные оценки за приемлемое время. Интеграция этих подходов гарантирует, что даже самые сложные многожизненные контракты могут быть оценены с необходимой точностью и надежностью, обеспечивая основу для эффективного управления рисками и принятия обоснованных финансовых решений.

Сравнение различных методов аппроксимации демонстрирует их влияние на величину ошибки.
Сравнение различных методов аппроксимации демонстрирует их влияние на величину ошибки.

Представленная работа демонстрирует стремление к построению более адекватной модели смертности, учитывающей взаимозависимости между застрахованными лицами. Это особенно важно при оценке стоимости совместных аннуитетов, где корреляция между жизнями играет ключевую роль. Данный подход, использующий линейно-рациональную структуру Вишарта, позволяет не только получить аналитические решения, но и более точно оценить риски, связанные с такими сложными финансовыми инструментами. Как однажды заметил Карл Саган: «Мы — звездная пыль, осознающая себя». В контексте данной работы, можно сказать, что модель стремится к осознанию сложности взаимосвязей в мире смертности, подобно тому, как звезда осознает свое место во Вселенной.

Куда же дальше?

Представленная работа, безусловно, вносит вклад в построение более адекватных моделей смертности, особенно в контексте оценки финансовых инструментов, зависящих от жизнеспособности нескольких лиц. Однако, не стоит обольщаться иллюзией полной достоверности. Линейно-рациональная структура, хоть и элегантна, всё же является упрощением реальности. Предположение о «гладкости» процесса Вишарта может оказаться недостаточным при анализе экстремальных событий, влияющих на популяции. Будущие исследования должны сосредоточиться на проверке робастности модели в условиях стресс-тестов и на включении в неё факторов, игнорируемых в текущей версии — например, влияние эпидемий или социальных потрясений.

Важным направлением представляется развитие методов калибровки модели на основе реальных данных. Простое соответствие историческим трендам недостаточно; необходимо учитывать неопределенность прогнозов и оценивать вероятность различных сценариев. Кроме того, следует обратить внимание на возможность расширения модели для учета зависимостей не только между членами семьи или супругами, но и между более широкими группами населения, объединенными общими факторами риска.

В конечном счете, ценность любой модели заключается не в её математической изысканности, а в её способности предсказывать будущее с приемлемой точностью. А будущее, как известно, всегда содержит сюрпризы. Поэтому, прежде чем возлагать на эту модель непомерные надежды, следует помнить старую поговорку: «Доверяй, но проверяй». И проверяй снова.

Оригинал статьи: https://arxiv.org/pdf/2602.06415.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-09 23:10