Неустойчивость в алгоритмах выбора: цена оптимальности

от

Автор: Денис Аветисян

Новое исследование показывает, что стремление к минимальным потерям в задачах выбора может привести к непредсказуемости и изменчивости в распределении ресурсов.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал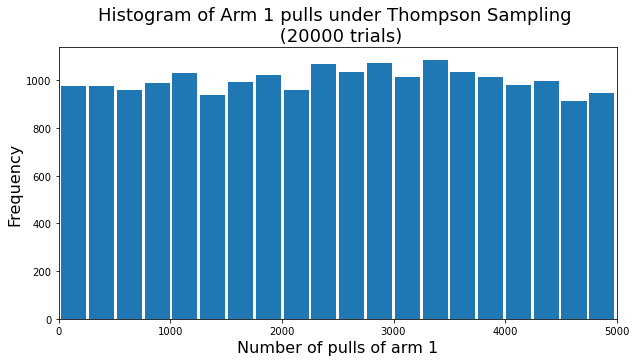
Распределение выборок, полученное с помощью алгоритма Thompson Sampling в примере 1.1, демонстрирует закономерности, определяющие стратегию исследования и эксплуатации в процессе обучения с подкреплением.
Распределение выборок, полученное с помощью алгоритма Thompson Sampling в примере 1.1, демонстрирует закономерности, определяющие стратегию исследования и эксплуатации в процессе обучения с подкреплением.

Работа устанавливает фундаментальный компромисс между минимизацией сожаления и вариативностью распределения в алгоритмах типа «многорукий бандит», определяя оптимальное положение на кривой Парето.

Несмотря на широкое применение многоруких бандитов, распределение выборок между альтернативными вариантами может быть крайне неравномерным. В работе, озаглавленной ‘Bandit Allocational Instability’, исследуется фундаментальный компромисс между минимизацией сожаления и дисперсией распределения, демонстрируя, что уменьшение одного показателя часто ведет к увеличению другого. В частности, показано, что для любого алгоритма справедливо неравенство R_T \cdot S_T = \Omega(T^{3/2}), где R_T — сожаление, а S_T — дисперсия распределения. Какие практические последствия имеет этот компромисс для платформ, использующих алгоритмы обучения с подкреплением, и как можно разработать алгоритмы, оптимально балансирующие между этими двумя показателями?

За пределами сожаления: Ограничения традиционных алгоритмов

Традиционные алгоритмы, известные как «разбойники с многорукими бандитами», в своей основе стремятся к минимизации понятия, называемого «сожалением». Сожаление представляет собой разницу между наградой, которую можно было бы получить, выбрав оптимальную стратегию, и фактической наградой, полученной алгоритмом в процессе обучения и эксплуатации ресурсов. Этот показатель, широко используемый для оценки эффективности алгоритмов, концентрируется исключительно на суммарном результате, игнорируя динамику процесса принятия решений. В результате, два алгоритма с одинаковым уровнем сожаления могут демонстрировать совершенно разные паттерны распределения ресурсов, что особенно важно в ситуациях, где важна стабильность и предсказуемость, например, при управлении рисками или работе с неоднородными данными. В фокусе минимизации сожаления алгоритмы могут демонстрировать чрезмерную изменчивость в выборе стратегий, что не всегда соответствует желаемому поведению.

Традиционные алгоритмы, ориентированные на минимизацию сожаления, зачастую не учитывают важный аспект — изменчивость распределения ресурсов. Хотя снижение общего сожаления и является важной целью, оно может скрывать нестабильность в процессе выбора действий. Представьте себе систему, которая в среднем показывает хорошие результаты, но при этом постоянно переключается между различными вариантами, что приводит к непредсказуемым колебаниям в распределении ресурсов. Такая изменчивость, незамеченная при анализе только сожаления, может быть критичной в ситуациях, когда важна стабильность, например, при работе с агентами, чувствительными к риску, или в условиях неидентичного и независимого распределения данных. Игнорирование этой изменчивости может привести к неоптимальным решениям, несмотря на низкое общее сожаление, и, следовательно, требует разработки новых метрик и алгоритмов, учитывающих динамику распределения ресурсов.

В задачах, где агенты чувствительны к риску или данные поступают не независимо и одинаково распределенными (non-IID), простое минимизирование сожаления может ввести в заблуждение относительно стабильности системы. Анализ паттернов распределения ресурсов становится критически важным, поскольку он позволяет выявить потенциальную нестабильность, которая не отражается в общей сумме полученных вознаграждений. Например, в финансовых приложениях или при управлении критически важной инфраструктурой, равномерное распределение ресурсов может быть предпочтительнее, даже если это приводит к незначительному снижению среднего вознаграждения, поскольку это уменьшает вероятность катастрофических потерь. Понимание того, как алгоритм распределяет ресурсы с течением времени, позволяет более точно оценить его пригодность для применения в условиях, где последовательность и надежность работы имеют первостепенное значение, а не только максимизация среднего дохода.

Введение в аллокационную стабильность как первичную цель

Вводится понятие вариативности распределения (allocation variability) как измеримая величина, характеризующая стабильность алгоритмов. Данный показатель количественно оценивает согласованность распределения ресурсов во времени. Высокая вариативность указывает на непоследовательное распределение, когда алгоритм существенно меняет приоритеты или объемы выделяемых ресурсов между итерациями или периодами времени. Формально, вариативность распределения определяется как мера отклонения фактического распределения ресурсов от ожидаемого или среднего распределения, что позволяет оценить предсказуемость и надежность алгоритма в динамической среде. Измерение вариативности распределения позволяет сравнивать различные алгоритмы с точки зрения их стабильности и предсказуемости, что критически важно для систем, требующих надежного и постоянного функционирования.

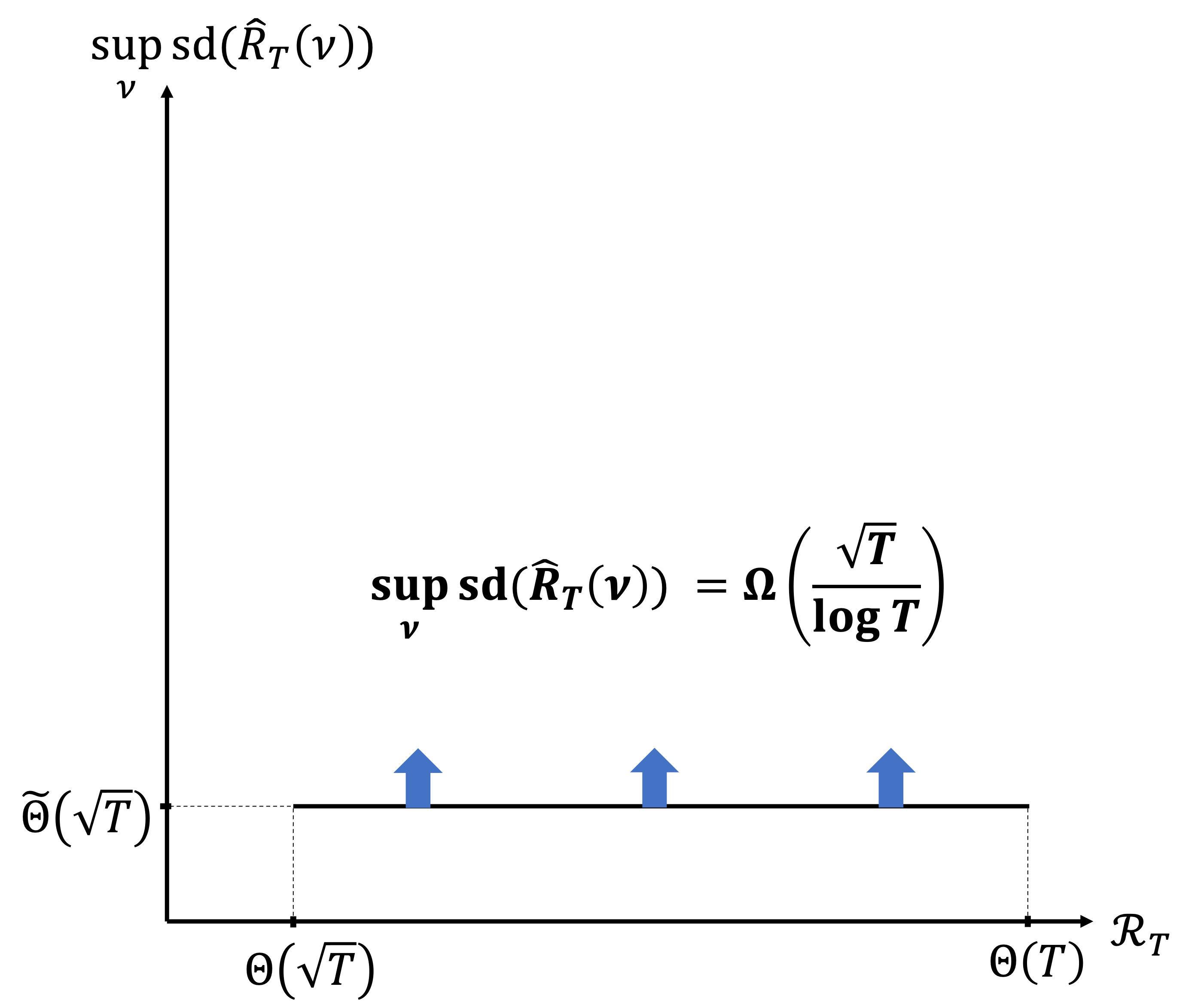
Новый подход к анализу стабильности алгоритмов выявил фундаментальный компромисс между минимизацией сожаления (regret) и вариативностью распределения ресурсов. Теоретически это подтверждено Теоремой о невозможности, которая устанавливает нижнюю границу для одновременной оптимизации этих двух показателей: ℛT⋅𝒮T=Ω(T3/2), где ℛT — суммарное сожаление за горизонт T, а 𝒮T — вариативность распределения ресурсов за тот же период. Данная нижняя граница означает, что в определенных сценариях невозможно одновременно добиться как минимального сожаления, так и минимальной вариативности распределения, что требует поиска баланса между этими целями.

Понятие Pareto-фронта возникает в контексте необходимости балансировки между минимизацией сожаления (regret) и вариативностью распределения ресурсов. Этот фронт представляет собой множество оптимальных решений, каждое из которых характеризуется определенным компромиссом между этими двумя конкурирующими целями. Любая точка на Pareto-фронте соответствует решению, при котором улучшение одного из критериев (например, снижение вариативности распределения) неизбежно приводит к ухудшению другого (увеличению сожаления), и наоборот. Таким образом, Pareto-фронт позволяет определить границы возможных оптимальных решений и выбрать наиболее подходящий вариант в зависимости от приоритетов конкретной задачи и допустимых потерь по каждому критерию. Формально, точки на Pareto-фронте представляют собой решения, не имеющие доминирующих альтернатив, то есть не существует другого решения, которое одновременно превосходило бы его по всем критериям.

Представленные кривые Парето демонстрируют компромиссы между различными целевыми функциями.
Представленные кривые Парето демонстрируют компромиссы между различными целевыми функциями.

UCB-f: Алгоритм балансировки исследования и стабильности

Алгоритм UCB-f представляет собой расширение классического алгоритма UCB1, разработанное для обеспечения управляемого компромисса между сожалением (regret) и изменчивостью распределения ресурсов (allocation variability). В отличие от UCB1, UCB-f позволяет пользователю контролировать баланс между стремлением к оптимальному решению и поддержанием стабильности процесса выбора действий. Это достигается путем введения параметра, влияющего на степень исследования (exploration) и эксплуатации (exploitation), что позволяет адаптировать алгоритм к конкретным требованиям задачи и минимизировать как суммарные потери, так и колебания в распределении ресурсов. В результате, UCB-f предоставляет более гибкий инструмент для решения задач многорукого бандита (multi-armed bandit), позволяя оптимизировать производительность в различных сценариях.

Алгоритм UCB-f использует методы FluidApproximation и PerturbationAnalysis для анализа своей производительности и получения гарантированных оценок как сожаления (regret), обозначаемого как ℛT = O(T<sup>1/2</sup>f(T)), так и вариативности распределения ресурсов, обозначаемого как 𝒮T = O(TlogTf(T)). Метод FluidApproximation позволяет аппроксимировать динамику алгоритма в непрерывном времени, упрощая анализ. PerturbationAnalysis, в свою очередь, используется для оценки влияния случайных флуктуаций на показатели алгоритма. Комбинация этих подходов позволяет строго доказать границы на величину сожаления и вариативности, что подтверждает эффективность UCB-f в балансировке между исследованием (exploration) и использованием (exploitation).

Теоретический анализ, включающий Theorem 3.1, демонстрирует нижнюю границу для взаимосвязи между накопленным сожалением (ℛT) и изменчивостью распределения ресурсов (𝒮T). В частности, доказано, что произведение этих метрик, ℛT ⋅ 𝒮T, имеет порядок не ниже Ω(T^{3/2}). Это подтверждает эффективность алгоритма UCB-f в достижении оптимального баланса между скоростью обучения (минимизацией сожаления) и стабильностью процесса распределения ресурсов, согласуясь с теоретически установленной нижней границей для данного типа задач.

Влияние на разработку надежных и адаптивных обучающих систем

В отличие от пассивных алгоритмов, UCB-f демонстрирует способность к активной адаптации стратегии распределения ресурсов, что обеспечивает устойчивость даже в динамически меняющихся условиях. Этот подход не ограничивается статичным выбором действий, а непрерывно оценивает и корректирует приоритеты, основываясь на поступающей информации о среде. В результате, UCB-f способен эффективно функционировать в ситуациях, где характеристики данных или вознаграждения изменяются со временем, что делает его особенно ценным в реальных приложениях, требующих надежности и гибкости. Такая адаптивность позволяет алгоритму сохранять высокую производительность, избегая застревания в неоптимальных решениях, свойственных менее гибким системам.

В условиях активного обучения, когда алгоритм самостоятельно выбирает, какие данные использовать для тренировки, особенно важной становится устойчивость к неидентично распределенным данным (Non-IID). Предлагаемый фреймворк демонстрирует особую эффективность в таких сценариях, поскольку он позволяет поддерживать стабильный процесс обучения даже при наличии значительных изменений в статистических свойствах поступающих данных. В отличие от традиционных подходов, которые могут испытывать трудности при работе с гетерогенными данными, данная система адаптируется к изменяющимся условиям, обеспечивая надежность и предсказуемость результатов обучения, что критически важно для практических приложений, где данные часто поступают из различных источников и имеют разное качество.

В условиях функционирования платформ с агентами, склонными к избежанию риска, предел минимизируемой функции потерь определяется выражением T \vee (T^3\rho^2 + 2\rho \wedge T). Данный результат указывает на то, что при значении параметра риска ρ, превышающем 2, процесс обучения становится неэффективным и целесообразно отказаться от дальнейшего сбора данных. В отличие от традиционной минимизации сожаления, предложенный подход обеспечивает более всестороннюю оценку алгоритмов типа «разбойник», учитывая не только накопленную прибыль, но и уровень риска. Это открывает перспективы для создания действительно адаптивных и надежных обучающих систем, способных эффективно функционировать в сложных и динамичных средах, где поведение агентов характеризуется высокой степенью непредсказуемости и нежеланием идти на неоправданный риск.

Исследование, представленное в данной работе, выявляет фундаментальный компромисс между минимизацией сожаления и вариативностью распределения ресурсов в алгоритмах типа «многорукий бандит». Этот компромисс, подобно тонкому балансу, требует от разработчиков осознанного выбора: снижение одного показателя часто ведет к увеличению другого. Как точно заметил Дональд Дэвис: «Простота — высшая форма изысканности». Действительно, стремление к оптимальному решению, к достижению Парето-фронта, требует ясного и лаконичного подхода к проблеме, отказа от излишних усложнений и сосредоточения на ключевых факторах, влияющих на стабильность и эффективность алгоритма. Сложность в данном контексте лишь замаскирует истинную природу проблемы, в то время как ясность позволит увидеть оптимальный путь.

Куда же дальше?

Работа, представленная в этой статье, выявила закономерность, которую многие предпочитали не замечать: стремление к минимизации сожаления в алгоритмах типа «многорукий бандит» неизбежно связано с увеличением вариативности распределения ресурсов. Они назвали это «торговым компромиссом», чтобы скрыть панику, вызванную осознанием того, что совершенство недостижимо. Истина, как всегда, проще: нельзя одновременно максимизировать прибыль и свести к нулю риск. Оптимальная паретовская граница — это не пункт назначения, а всего лишь линия, очерчивающая область допустимого.

Однако, истинное понимание проблемы — это лишь первый шаг. Остается вопрос о том, как эта вариативность влияет на агентов, не склонных к риску, и как она проявляется в условиях не-i.i.d. данных — условиях, которые, как известно, гораздо ближе к реальности, чем наивные предположения большинства теоретических моделей. Следующим этапом представляется разработка алгоритмов, которые не просто достигают оптимальной границы, но и учитывают индивидуальные предпочтения агентов и структуру данных.

И, конечно, стоит помнить, что любое «решение» — это всего лишь временная остановка в бесконечном потоке усложнений. Упрощение — вот что действительно важно. Возможно, в будущем, вместо того чтобы изобретать все более сложные алгоритмы, стоит сосредоточиться на создании систем, которые учатся адаптироваться к изменениям, не требуя постоянного вмешательства человека. Это, пожалуй, и будет настоящим прогрессом.

Оригинал статьи: https://arxiv.org/pdf/2602.07472.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-10 23:06