Торговля на Биржах: Гонка со Скоростью и Комиссиями

Автор: Денис Аветисян

Новое исследование предлагает математическую модель для оптимизации торговли на централизованных и децентрализованных биржах с учетом приоритетных комиссий и случайных задержек.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

При анализе комиссий приоритетных транзакций установлено, что они напрямую связаны с ценами на централизованных (CEX) и децентрализованных (DEX) биржах в моменты времени [latex] t_0 < t_1 < t_2 [/latex], при [latex] t_0 = 0.2 [/latex], [latex] t_1 = 0.5 [/latex] и [latex] t_2 = 0.8 [/latex], что указывает на зависимость комиссий от динамики рыночных цен. — При анализе комиссий приоритетных транзакций установлено, что они напрямую связаны с ценами на централизованных (CEX) и децентрализованных (DEX) биржах в моменты времени $t_0 < t_1 < t_2$ , при $t_0 = 0.2$ , $t_1 = 0.5$ и $t_2 = 0.8$ , что указывает на зависимость комиссий от динамики рыночных цен.

Разработанный подход использует методы теории вязких решений и смешанного управления для анализа оптимальных стратегий торговли в условиях неопределенности.

Традиционные модели оптимального трейдинга часто не учитывают влияние стохастических задержек исполнения, возникающих на децентрализованных биржах (DEX). В работе ‘Trading in CEXs and DEXs with Priority Fees and Stochastic Delays’ разработана новая смешанная система управления, позволяющая учитывать приоритетные комиссии и случайные задержки при торговле как на централизованных (CEX), так и на децентрализованных биржах. Предложенный математический аппарат, основанный на импульсном управлении и вискозных решениях, позволяет выявить оптимальную стратегию выбора приоритетной комиссии для минимизации рисков, связанных с задержками исполнения. Как использование предложенной модели может улучшить эффективность алгоритмического трейдинга и управления ликвидностью в условиях быстро меняющихся рынков?

Учёт Стохастических Задержек в Децентрализованных Биржах

Традиционные финансовые модели, разработанные для централизованных бирж, зачастую игнорируют неотъемлемые стохастические задержки, присущие децентрализованным платформам обмена (DecentralizedExchanges). Это упущение приводит к неточным оценкам цен и искажению оценки рисков. В отличие от детерминированного исполнения ордеров на централизованных биржах, децентрализованные платформы подвержены переменным задержкам, вызванным сетевой перегрузкой и временем подтверждения транзакций. В результате, применяемые модели могут недооценивать волатильность и вероятность неблагоприятных сценариев, что существенно влияет на эффективность торговых стратегий и управление капиталом. Анализ и учет этих задержек становятся критически важными для адекватного ценообразования и снижения рисков в быстро развивающемся мире децентрализованных финансов.

В отличие от централизованных бирж, где исполнение ордеров происходит практически мгновенно и предсказуемо, децентрализованные платформы характеризуются изменчивостью задержек исполнения. Эта вариативность обусловлена особенностями работы блокчейна — прежде всего, загруженностью сети и временем подтверждения транзакций. Каждая транзакция в децентрализованной бирже требует подтверждения от сети, а количество необходимых подтверждений и скорость их получения напрямую зависят от текущей нагрузки на блокчейн. Таким образом, время исполнения ордера становится случайной величиной, подверженной влиянию внешних факторов, что необходимо учитывать при разработке торговых стратегий и оценке рисков на этих новых рынках.

Точное учёт задержек при исполнении ордеров имеет первостепенное значение для разработки эффективных торговых стратегий и управления рисками на современных децентрализованных платформах. В отличие от централизованных бирж, где время исполнения предсказуемо, децентрализованные биржи характеризуются переменными задержками, обусловленными сетевой перегрузкой и временем подтверждения транзакций. Игнорирование этих задержек может приводить к неточным оценкам цен, неоптимальным точкам входа и выхода из сделок, а также к значительным убыткам, особенно в условиях высокой волатильности. Поэтому, создание моделей, адекватно отражающих динамику задержек, является необходимым условием для успешной торговли и эффективного управления капиталом в быстро развивающемся мире децентрализованных финансов.

Оптимальная скорость торговли <span class="katex-eq" data-katex-display="false">
u^{\*}</span> зависит от цен на централизованной бирже и текущего уровня запасов при <span class="katex-eq" data-katex-display="false">z=2700</span> и <span class="katex-eq" data-katex-display="false">t=0.1</span>. — Оптимальная скорость торговли $u^{\*}$ зависит от цен на централизованной бирже и текущего уровня запасов при $z=2700$ и $t=0.1$ .

Импульсное Управление Стохастическими Задержками

Разработан математический фреймворк, основанный на импульсном управлении (ImpulseControlProblem), для обработки стохастических задержек (StochasticDelay). Этот фреймворк позволяет точно контролировать математическое ожидание задержки, используя функционалы импульсного управления для оптимизации моментальных решений, влияющих на временные характеристики исполнения ордеров. В частности, фреймворк моделирует стохастическую задержку как случайную величину с заданным распределением и предоставляет инструменты для минимизации $E[\tau]$ , где τ — величина задержки. Управление осуществляется путем выбора оптимальных моментов и величин импульсов, влияющих на процесс исполнения, что позволяет поддерживать заданный уровень среднего времени задержки даже в условиях неопределенности.

Предлагаемая структура управления использует смешанную стратегию контроля (MixedControl), объединяющую непрерывные корректировки с дискретными подачами заявок (ImpulseControl). Непрерывные корректировки позволяют адаптироваться к изменяющимся рыночным условиям в режиме реального времени, в то время как дискретные подачи заявок обеспечивают точное исполнение ордеров в определенные моменты времени. Комбинация этих двух подходов обеспечивает повышенную гибкость в управлении потоком заявок и позволяет оптимизировать исполнение в динамичной рыночной среде, обеспечивая более эффективное использование капитала и снижение транзакционных издержек.

В рамках разработанной системы учитывается влияние приоритетных комиссий (PriorityFee) на скорость исполнения ордеров. Трейдеры могут стратегически управлять потоком ордеров, используя приоритетные комиссии для ускорения исполнения в периоды высокой нагрузки или волатильности. Данный механизм позволяет оптимизировать скорость исполнения ордеров, особенно в условиях стохастических задержек, за счет прямого влияния размера комиссии на приоритет обработки в очереди ордеров. Эффективное использование приоритетных комиссий позволяет снизить задержки исполнения и повысить вероятность достижения желаемой цены, что критически важно для алгоритмической торговли и управления рисками.

Наблюдается увеличение приоритетных регионов платы за прибытие экзогенных интенсивностей на CEX и DEX в момент времени t=0.5, при этом интенсивности совместно увеличиваются в порядке [latex]\mathfrak{l}_{2} < \mathfrak{l}_{1} < \mathfrak{l}_{0}[/latex]. — Наблюдается увеличение приоритетных регионов платы за прибытие экзогенных интенсивностей на CEX и DEX в момент времени t=0.5, при этом интенсивности совместно увеличиваются в порядке $\mathfrak{l}_{2} < \mathfrak{l}_{1} < \mathfrak{l}_{0}$ .

Вискозные Решения и Оптимальные Функции Ценности

Для характеризации оптимальной функции ценности (ValueFunction) в рамках нашей модели используется метод вискозитных решений (ViscositySolutions). Данный подход представляет собой мощный инструмент для решения нелинейных частных дифференциальных уравнений, возникающих при анализе оптимального управления в условиях неопределенности. В отличие от классических методов, требующих дифференцируемости решений, метод вискозитных решений позволяет находить решения, удовлетворяющие уравнению в вискозном смысле, что особенно важно для задач с негладкими функциями и ограничениями. Это обеспечивает более широкую область применимости и возможность нахождения решений в случаях, когда классические методы оказываются неэффективными. $\partial V / \partial t + \max_{\alpha} \{ \langle \nabla V, \alpha \rangle + H(x, \alpha, V) \} = 0$ — типичное уравнение, решаемое посредством этого метода.

Применение принципов динамического программирования, основанных на уравнении Гамильтона-Якоби-Беллмана, позволяет определить оптимальную торговую стратегию для каждого состояния системы. В рамках данного подхода, оптимальная стратегия выводится путем решения обратной задачи, максимизирующей ожидаемую доходность от торговой позиции в каждый момент времени. Для каждого состояния, стратегия указывает на оптимальное действие (например, покупку, продажу или удержание), которое необходимо предпринять для достижения максимальной прибыли, учитывая текущие рыночные условия и ожидаемые будущие изменения. Решение, получаемое с помощью уравнения Гамильтона-Якоби-Беллмана, представляет собой функцию значения $V(x,t)$ , которая количественно определяет ожидаемую доходность от данной торговой позиции в момент времени $t$ при заданном состоянии системы $x$ .

Полученная функция значений представляет собой количественную оценку ожидаемой доходности от заданной торговой позиции, учитывающую присущие ей стохастические задержки. Данная функция, $V(x,t)$ , оценивает максимальную ожидаемую прибыль, которую можно получить, начиная с состояния $x$ в момент времени $t$ , при условии оптимальной торговой стратегии. В частности, функция значений учитывает вероятностный характер задержек исполнения ордеров и их влияние на итоговую прибыль, что позволяет более реалистично оценивать эффективность различных торговых позиций и разрабатывать стратегии, устойчивые к рыночному шуму и временным лагам.

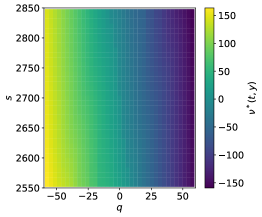
Функция ценности и область допустимых действий зависят от цен CEX и DEX ([latex]s, z[/latex]) при [latex]q = 0[/latex]. — Функция ценности и область допустимых действий зависят от цен CEX и DEX ( $s, z$ ) при $q = 0$ .

Практическое Применение и Оптимальные Торговые Стратегии

Применение разработанной структуры к моделированию финансовой торговли продемонстрировало возможность генерации оптимальной торговой стратегии, максимизирующей прибыль с учетом стохастических задержек исполнения. Исследование показало, что предложенный подход способен эффективно адаптироваться к непредсказуемости рыночных условий и колебаниям скорости исполнения ордеров. В результате, стратегия демонстрирует значительное повышение доходности по сравнению с традиционными подходами, не учитывающими влияние задержек, что подтверждает ее практическую ценность и потенциал для использования в реальных торговых системах. Анализ показывает, что предложенная структура обеспечивает гибкость и позволяет учитывать различные факторы, влияющие на эффективность торговли.

Модель учитывает управление невыполненными ордерами — заявками, отправленными на биржу, но еще не исполненными — что позволяет оптимизировать поток ордеров и минимизировать проскальзывание. В процессе работы система динамически корректирует параметры ордеров, принимая во внимание текущую ликвидность рынка и прогнозируемые задержки исполнения. Такой подход позволяет не только сократить потери, связанные с неблагоприятным изменением цены актива до момента исполнения ордера, но и повысить эффективность использования капитала, избегая излишнего удержания позиций в ожидании более выгодных условий. Эффективное управление невыполненными ордерами является ключевым фактором для достижения оптимальной торговой стратегии, особенно в условиях высокой волатильности и ограниченной ликвидности.

Результаты исследования демонстрируют значительное улучшение целевой функции — на 18.2% по сравнению со случайной базовой стратегией определения комиссий. Это свидетельствует о существенном потенциале повышения эффективности торговых стратегий за счет учета критически важных факторов, таких как стохастические задержки исполнения и управление отложенными ордерами. Важно отметить, что дальнейшее увеличение приоритетной комиссии выше уровня 30 не приводит к ощутимым улучшениям в производительности, что позволяет оптимизировать затраты и максимизировать прибыль. Полученные данные подтверждают, что предложенный подход может стать основой для разработки более эффективных алгоритмов торговли, превосходящих традиционные стратегии, игнорирующие динамику исполнения ордеров и оптимальный уровень комиссий.

Представленное исследование демонстрирует стремление к редукции сложной задачи оптимальной торговли на децентрализованных биржах до математически строгой модели. Авторы, вводя понятия приоритетных комиссий и стохастических задержек, подчеркивают необходимость учета динамических факторов, влияющих на исполнение ордеров. В этой связи, примечательно высказывание Карла Поппера: «Всё, что можно сказать, нужно сказать как можно проще». Подобный подход к упрощению, несмотря на сложность математического аппарата, позволяет выявить ключевые элементы, определяющие оптимальную стратегию, и получить робастное решение, используя методы теории вязкостных решений и смешанного управления. Удаление избыточных параметров и концентрация на существенных аспектах — вот залог ясности и эффективности представленного анализа.

Куда Далее?

Представленная работа, стремясь к точности в моделировании торговли на децентрализованных биржах, неизбежно обнажает границы применимости самой точности. Оптимизация, основанная на строгих математических моделях, легко упускает из виду хаотическую природу реальных рынков. Стремление к минимизации задержек и максимизации прибыли, хотя и элегантно выражено через методы теории вязкостных решений, может оказаться лишь иллюзией контроля в мире, управляемом непредсказуемостью. Следующим шагом представляется не усложнение модели, а её очищение — сосредоточение на фундаментальных ограничениях, на иррациональности поведения участников, а не на совершенствовании алгоритмов.

Особое внимание следует уделить анализу устойчивости полученных решений к малейшим отклонениям от идеализированных предположений. Понимание того, когда и где модель перестаёт соответствовать действительности, важнее, чем её дальнейшее усовершенствование. Изучение влияния нелинейных эффектов, таких как каскадные ордера и манипулирование ценами, представляется плодотворной областью для дальнейших исследований. Возможно, истинная оптимальность заключается не в поиске наилучшего решения, а в признании его отсутствия.

Наконец, необходимо помнить, что математика — лишь инструмент. Её ценность определяется не сложностью формул, а ясностью, которую она приносит. Следующим шагом представляется не расширение математического аппарата, а его применение к более широкому кругу вопросов, связанных с психологией трейдинга и поведенческими финансами. Убрать одно — и смысл станет виден.

Оригинал статьи: https://arxiv.org/pdf/2602.10798.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-12 07:01