Разделяй и Властвуй в Многокритериальной Оптимизации

от

Автор: Денис Аветисян

Новый подход к решению сложных комбинаторных задач позволяет эффективно находить оптимальные решения, учитывая сразу несколько целей.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал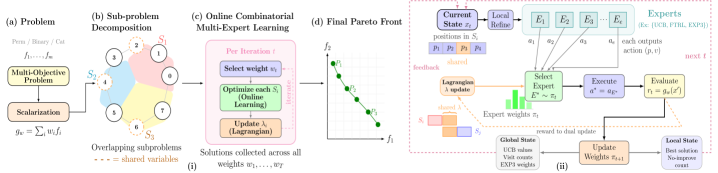
В рамках подхода D&L, любая многоцелевая задача преобразуется в набор пересекающихся подзадач со общими переменными, где оптимизация каждой подзадачи осуществляется на основе принципов обучения с подкреплением, а обеспечение согласованности между подзадачами достигается посредством двойственности Лагранжа и координации с использованием множителей Лагранжа, что позволяет эффективно исследовать экспоненциально большие пространства решений посредством амортизации разведки и выбора действий на основе смешанных стратегий, включающих алгоритмы UCB, FTRL, EXP3 и TS.
В рамках подхода D&L, любая многоцелевая задача преобразуется в набор пересекающихся подзадач со общими переменными, где оптимизация каждой подзадачи осуществляется на основе принципов обучения с подкреплением, а обеспечение согласованности между подзадачами достигается посредством двойственности Лагранжа и координации с использованием множителей Лагранжа, что позволяет эффективно исследовать экспоненциально большие пространства решений посредством амортизации разведки и выбора действий на основе смешанных стратегий, включающих алгоритмы UCB, FTRL, EXP3 и TS.

Предлагается фреймворк Divide & Learn, использующий алгоритмы bandit для декомпозиции задач многокритериальной комбинаторной оптимизации и достижения масштабируемости без привлечения суррогатных моделей или предварительного обучения.

Многокритериальная комбинаторная оптимизация, несмотря на свою важность, часто сталкивается с ограничениями масштабируемости и отсутствием теоретических гарантий. В данной работе, озаглавленной ‘Divide and Learn: Multi-Objective Combinatorial Optimization at Scale’, предложен новый подход, формулирующий задачу как процесс онлайн-обучения над декомпозированным пространством решений. Этот метод, основанный на алгоритмах bandit-оптимизации, позволяет достичь границ сожаления порядка O(d\sqrt{T \log T}), зависящих от размерности подзадач, а не от размера всего пространства. Может ли декомпозиция пространства решений стать ключевым элементом в разработке эффективных алгоритмов для решения сложных многокритериальных задач?

Вызов Комбинаторной Сложности

Многие задачи, с которыми сталкиваются современные исследователи и инженеры, такие как классическая задача коммивояжера или проблема рюкзака, относятся к классу мультиобъективной комбинаторной оптимизации. Суть этих задач заключается в поиске наилучшего решения, учитывающего сразу несколько, часто противоречивых, критериев. Однако, количество возможных вариантов решений растет экспоненциально с увеличением масштаба задачи, что делает полный перебор невозможным даже для современных вычислительных мощностей. Данная вычислительная неразрешимость, известная как NP-трудность, означает, что поиск гарантированно оптимального решения требует времени, растущего экспоненциально с размером входных данных, что делает решение таких задач крайне сложным и часто требует применения приближенных алгоритмов или эвристик.

Традиционные методы оптимизации, такие как полный перебор или динамическое программирование, сталкиваются с серьезными ограничениями при решении задач, где количество возможных решений растет экспоненциально с увеличением масштаба проблемы. Это связано с тем, что объем вычислений, необходимый для проверки каждого варианта, быстро становится непосильным даже для современных вычислительных систем. Например, при увеличении числа элементов в задаче коммивояжера на единицу, количество потенциальных маршрутов увеличивается в разы, что делает поиск оптимального решения непрактичным. В результате, эти методы оказываются неэффективными при масштабировании и не способны обеспечить приемлемое время отклика для задач, имеющих хоть сколько-нибудь значительный размер, что ограничивает их применимость в реальных сценариях, требующих оперативной оптимизации.

Ограничения, возникающие при решении задач комбинаторной оптимизации, оказывают существенное влияние на прогресс в различных областях. В логистике, например, оптимизация маршрутов доставки и управления цепочками поставок сталкивается с трудностями при увеличении масштаба и сложности задач, что приводит к увеличению затрат и снижению эффективности. Аналогично, в сфере распределения ресурсов, будь то финансовые активы, энергетические мощности или вычислительные ресурсы, невозможность быстрого нахождения оптимальных решений ограничивает возможности планирования и адаптации к изменяющимся условиям. Особенно заметно это проявляется в современной аппаратной и программной совместной разработке, где оптимизация взаимодействия между компонентами требует учета огромного количества параметров и конфигураций, а традиционные методы оказываются неспособными обеспечить требуемую производительность и энергоэффективность систем.

Для преодоления трудностей, связанных с комбинаторной сложностью, разрабатываются инновационные подходы, направленные на эффективное исследование огромных пространств решений. Эти методы включают в себя алгоритмы, основанные на метаэвристиках, такие как генетические алгоритмы и имитация отжига, которые позволяют находить приближённо оптимальные решения за разумное время. Особое внимание уделяется техникам декомпозиции, разбивающим сложную задачу на более мелкие, управляемые подзадачи. Кроме того, перспективным направлением является использование машинного обучения для прогнозирования эффективности различных стратегий поиска и адаптации алгоритмов к специфике конкретной задачи. Эти усилия направлены на создание инструментов, способных решать сложные оптимизационные проблемы в различных областях, от логистики и распределения ресурсов до проектирования аппаратного и программного обеспечения.

Анализ динамики координации показывает, что лагранжева координация обеспечивает более стабильную оптимизацию (сужающиеся полосы доверия на графике вознаграждений), влияя на траекторию вознаграждений, а не на динамику оценок ценности, что подтверждается схожей эволюцией дисперсии и показателя разногласия в обеих условиях.
Анализ динамики координации показывает, что лагранжева координация обеспечивает более стабильную оптимизацию (сужающиеся полосы доверия на графике вознаграждений), влияя на траекторию вознаграждений, а не на динамику оценок ценности, что подтверждается схожей эволюцией дисперсии и показателя разногласия в обеих условиях.

Разделяй и Учись: Новый Подход к Оптимизации

Метод “Разделяй и Учись” представляет собой принципиально новый подход к комбинаторной оптимизации, рассматривающий задачу не как единое целое, а как последовательный онлайн-процесс. Вместо поиска оптимального решения за один шаг, данный метод разбивает проблему на серию последовательных решений, принимаемых на каждом этапе. Такой подход позволяет эффективно исследовать пространство решений, избегая затратных полных переборов и фокусируясь на наиболее перспективных областях. В отличие от традиционных методов, требующих предварительного знания всей задачи, “Разделяй и Учись” адаптируется в процессе работы, используя информацию, полученную на предыдущих шагах, для улучшения качества принимаемых решений и повышения скорости сходимости к оптимальному результату.

Стратегия декомпозиции, являющаяся ключевым элементом метода, предполагает разделение сложной комбинаторной задачи на более мелкие, управляемые подзадачи. Этот процесс облегчает поиск решения, поскольку позволяет сосредоточиться на оптимизации отдельных компонентов. Координация между подзадачами осуществляется с использованием методов, таких как релаксация Лагранжа L(x, \lambda) = f(x) + \sum_{i=1}^{m} \lambda_i c_i(x), где f(x) — целевая функция, c_i(x) — ограничения, а \lambda_i — множители Лагранжа. Релаксация Лагранжа позволяет ослабить ограничения, преобразуя исходную задачу в более простую, которую легче решить, и итеративно корректировать множители Лагранжа для приближения к оптимальному решению исходной задачи.

Ключевым элементом эффективности метода Divide & Learn является использование Position-Wise Bandits для принятия обоснованных решений на каждом шаге процесса оптимизации. В основе работы Position-Wise Bandits лежит принцип обучения с подкреплением, где каждое «действие» соответствует выбору определенной стратегии решения подзадачи. В отличие от традиционных подходов, использующих ограниченную информацию, здесь применяется Full-Bandit Feedback — полная обратная связь о результатах каждого действия, включающая оценку качества полученного решения и информацию о его влиянии на общую целевую функцию. Это позволяет алгоритму адаптироваться в реальном времени, эффективно исследовать пространство решений и быстро находить оптимальные или близкие к оптимальным решения, максимизируя получаемое вознаграждение на каждом шаге.

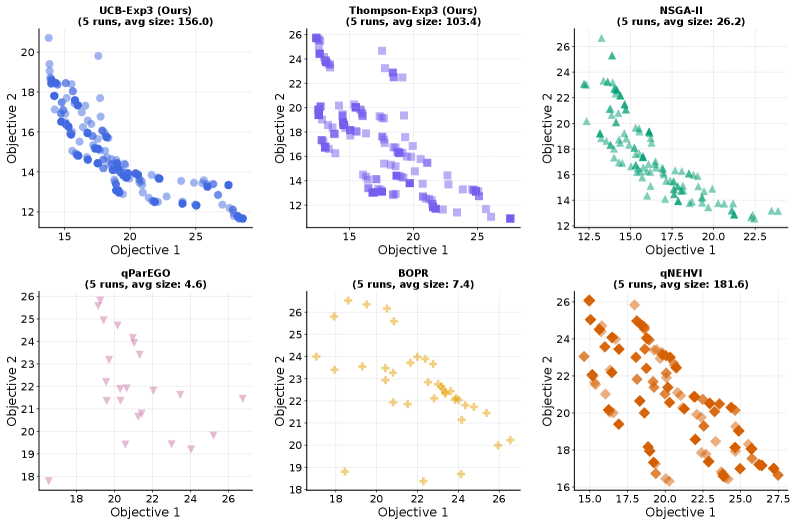
Методика «Разделяй и Учись» обеспечивает адаптивное исследование и использование пространства решений, преодолевая ограничения традиционных методов оптимизации. В отличие от статических алгоритмов, данный подход динамически корректирует стратегию поиска, балансируя между изучением новых областей и углублением в перспективные. В результате, в тестах на различных задачах комбинаторной оптимизации, производительность метода достигает 80-98% от эффективности специализированных решателей, разработанных для конкретных типов задач. Это делает его универсальным и эффективным инструментом для широкого спектра применений, где требуется нахождение оптимальных или близких к оптимальным решений.

В задачах BiTSP20 и BiTSP50, координация на основе лагранжевых множителей значительно снижает разброс вознаграждений (на 95% для BiTSP20 и на 19% для BiTSP50) и обеспечивает высокую частоту успешных решений (80% и 60% соответственно), при этом динамика двойственных переменных подтверждает эффективное отслеживание нарушений координации.
В задачах BiTSP20 и BiTSP50, координация на основе лагранжевых множителей значительно снижает разброс вознаграждений (на 95% для BiTSP20 и на 19% для BiTSP50) и обеспечивает высокую частоту успешных решений (80% и 60% соответственно), при этом динамика двойственных переменных подтверждает эффективное отслеживание нарушений координации.

Множество Экспертов: Надежность в Оптимизации

Методология Divide & Learn использует подход “Множество Экспертов”, применяя различные алгоритмы, такие как UCB (Upper Confidence Bound), EXP3 (Exponential-weight Algorithm for Exploration & Exploitation) и FTRL (Follow The Regularized Leader), для исследования пространства решений с разных точек зрения. Каждый из этих алгоритмов использует свою собственную стратегию: UCB основывается на верхней границе доверительного интервала, EXP3 обеспечивает устойчивость к неблагоприятным условиям, а FTRL оптимизирует распределение с регуляризацией. Использование нескольких экспертов позволяет более эффективно исследовать пространство решений и находить оптимальные решения, чем при использовании одного алгоритма.

В рамках подхода “Divide & Learn” используются различные алгоритмы, именуемые “экспертами”, каждый из которых применяет свою уникальную стратегию поиска решения. Алгоритм UCB (Upper Confidence Bound) основывается на использовании верхних границ доверительных интервалов для оценки перспективности различных вариантов, стимулируя исследование менее изученных областей. EXP3 (Exponential-weight Algorithm for Exploration & Exploitation) обеспечивает устойчивость к неблагоприятным воздействиям, адаптируясь к изменяющимся условиям и минимизируя риски. FTRL (Follow The Regularized Leader) оптимизирует распределение вероятностей с применением регуляризации, что позволяет эффективно находить баланс между исследованием и использованием известных решений. Сочетание этих различных стратегий обеспечивает более полное и всестороннее исследование пространства решений.

В дополнение к алгоритмам UCB, EXP3 и FTRL, в рамках подхода Divide & Learn используется семплирование по Томпсону (Thompson Sampling) как еще одна стратегия исследования пространства решений. Данный метод, основанный на вероятностном подходе, позволяет генерировать образцы действий на основе апостериорного распределения вероятностей, что способствует более широкому и разнообразному исследованию, особенно в сложных задачах оптимизации. Интеграция семплирования по Томпсону расширяет возможности адаптации к различным характеристикам задачи и повышает надежность получаемых решений, дополняя стратегии, основанные на верхних границах доверия и регуляризации.

Использование ансамбля экспертных алгоритмов позволяет данной системе адаптироваться к различным характеристикам решаемой задачи и обеспечивать устойчивые решения. В ходе тестирования на множестве эталонных наборов данных, предложенный подход демонстрирует улучшение результатов в диапазоне от 20% до 90% по сравнению с базовыми байесовскими методами. Такая эффективность достигается за счет комбинирования различных стратегий исследования и оптимизации, что позволяет системе эффективно справляться с задачами, обладающими разнообразными свойствами и требованиями.

Эксперименты с BiTSP-20 показали, что предложенный механизм выбора EXP3/FTRL снижает сожаление, а декомпозиция пространства задач значительно улучшает покрытие фронта Парето.
Эксперименты с BiTSP-20 показали, что предложенный механизм выбора EXP3/FTRL снижает сожаление, а декомпозиция пространства задач значительно улучшает покрытие фронта Парето.

Суррогатные Модели и Будущее Оптимизации

Существующие методы, основанные на суррогатных моделях, такие как мультиобъективная байесовская оптимизация, представляют собой эффективный способ аппроксимации сложных целевых функций, что позволяет значительно снизить вычислительные затраты. Вместо прямого вычисления дорогостоящей функции, суррогатная модель, построенная на основе небольшого числа вычислений, используется для предсказания ее значений. Этот подход особенно ценен при решении задач, где каждое вычисление функции требует значительных ресурсов или времени. Благодаря использованию гауссовских процессов, суррогатные модели способны не только предсказывать значения функции, но и оценивать связанную с этим неопределенность, что позволяет более обоснованно принимать решения в процессе оптимизации и эффективно исследовать пространство поиска.

Многоцелевая байесовская оптимизация, используя Гауссовские процессы, предоставляет не только вероятностные прогнозы целевой функции, но и оценки неопределенности этих прогнозов. Этот подход позволяет значительно улучшить процесс принятия решений в рамках стратегии “Разделяй и Учись”. Гауссовские процессы, по сути, позволяют оценить, насколько надежны полученные предсказания, что критически важно при исследовании сложных оптимизационных ландшафтов. Возможность количественно оценить неопределенность позволяет алгоритму более эффективно выбирать следующие точки для исследования, фокусируясь на областях, где информация наиболее ценна, и избегая заведомо неоптимальных решений. Такой подход не только повышает скорость сходимости, но и обеспечивает более надежные и обоснованные результаты, особенно в ситуациях, когда данные ограничены или зашумлены.

Нейронная комбинаторная оптимизация становится перспективным направлением, использующим возможности нейронных сетей для обучения стратегиям поиска и, как следствие, ускорения процесса оптимизации. В отличие от традиционных методов, требующих полного перебора вариантов, нейронные сети способны выявлять закономерности и предсказывать наиболее эффективные пути решения задачи. Этот подход позволяет значительно сократить время вычислений, особенно в сложных задачах комбинаторной оптимизации, где количество возможных решений экспоненциально растет. Обученные нейронные сети эффективно осваивают эвристики поиска, адаптируясь к специфике каждой задачи и предоставляя решения, сравнимые, а зачастую и превосходящие по качеству, результаты, полученные традиционными методами.

Современные достижения в области суррогатных моделей открывают принципиально новые возможности для решения задач оптимизации, ранее считавшихся недоступными из-за их вычислительной сложности. Эти усовершенствования позволяют значительно сократить затраты на вычисления — на 90-99% по сравнению с традиционными методами байесовской оптимизации — и при этом превосходить по эффективности нейронные решатели, обученные заранее, на 50-70% при сопоставимых вычислительных ресурсах. Такой прогресс способствует развитию инноваций в самых разных областях — от разработки новых материалов и лекарственных препаратов до оптимизации логистических цепочек и управления энергетическими системами — позволяя решать задачи, которые ранее требовали непомерных вычислительных мощностей и времени.

Предложенные методы демонстрируют плотные и равномерно распределенные Парето-фронты на BiTSP-50, сопоставимые с NSGA-II, но с существенно меньшими вычислительными затратами.
Предложенные методы демонстрируют плотные и равномерно распределенные Парето-фронты на BiTSP-50, сопоставимые с NSGA-II, но с существенно меньшими вычислительными затратами.

Исследование, представленное в данной работе, демонстрирует подход к решению многокритериальной комбинаторной оптимизации, основанный на декомпозиции сложных задач на более мелкие подзадачи. Это напоминает о важности постепенных изменений и адаптации систем к текущим условиям. Как однажды заметил Г.Х. Харди: «Математика — это наука о том, что не знаем». Подобно этому, и представленный алгоритм Divide & Learn, постоянно исследует пространство решений, стремясь к оптимальному балансу между различными критериями, осознавая, что полное знание недостижимо. Акцент на декомпозиции позволяет алгоритму справляться с масштабируемостью, избегая при этом сложностей, связанных с предварительным обучением или использованием суррогатных моделей, что соответствует принципам долговечности и устойчивости систем.

Что впереди?

Представленный подход, декомпозирующий многокритериальную комбинаторную оптимизацию на управляемые подзадачи посредством алгоритмов «разбойников», безусловно, демонстрирует жизнеспособность. Однако, следует признать, что любое деление — это упрощение, а любое упрощение — это потеря информации. Система, хоть и эффективная в данный момент, не избежит эрозии, вызванной возрастающей сложностью решаемых задач. Стабильность, достигнутая за счет декомпозиции, может оказаться лишь отсрочкой неизбежного столкновения с пределами масштабируемости.

Наиболее перспективным направлением представляется не столько совершенствование существующих алгоритмов «разбойников», сколько разработка принципиально новых методов, способных учитывать взаимосвязи между подзадачами, возникающие в процессе декомпозиции. Необходимо перейти от решения отдельных подзадач к построению целостной картины, учитывающей синергию и антагонизм между ними. Иначе говоря, требуется не просто «разделять и властвовать», а «разделять и понимать».

Следует также признать, что понятие «оптимальности Парето» — это лишь снимок текущего состояния системы. Время — не метрика, а среда, и оптимальное решение сегодня может оказаться совершенно непригодным завтра. Поэтому, дальнейшие исследования должны быть направлены на разработку адаптивных алгоритмов, способных динамически реагировать на изменения в окружающей среде и пересматривать свои решения в соответствии с новыми условиями. В конечном итоге, задача состоит не в том, чтобы найти «лучшее» решение, а в том, чтобы обеспечить устойчивость системы во времени.

Оригинал статьи: https://arxiv.org/pdf/2602.11346.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-13 21:31