Прогнозирование временных рядов: новый подход к долгосрочным зависимостям

Автор: Денис Аветисян

Исследователи предлагают инновационную архитектуру для повышения точности прогнозирования многомерных временных рядов, особенно на больших временных горизонтах.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал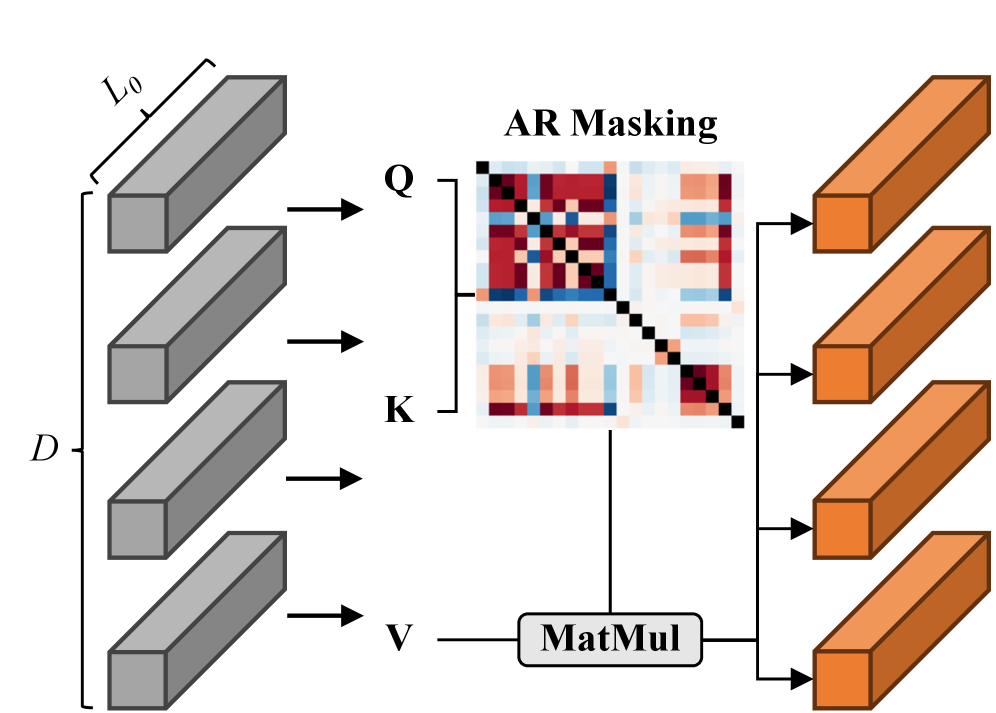

Архитектура AltTS предполагает параллельную обработку многомерных временных рядов посредством двух путей: авторегрессионного (AR), независимого от каналов, и кросс-реляционного (CR), учитывающего зависимости между каналами, причём суммирование их результатов формирует окончательный прогноз, а применение AR-маски к матрице внимания в кросс-реляционном пути подавляет внутрисерийные связи, обеспечивая акцент на межсерийных взаимосвязях.

В статье представлена AltTS — глубокая нейронная сеть, использующая чередующуюся оптимизацию для эффективной обработки авторегрессионных и межпеременных зависимостей.

Прогнозирование многомерных временных рядов осложняется конфликтом между стабильными авторегрессионными зависимостями и преходящими межпеременными взаимодействиями. В данной работе, посвященной разработке фреймворка ‘AltTS: A Dual-Path Framework with Alternating Optimization for Multivariate Time Series Forecasting’, предложен подход, основанный на разделении моделирования авторегрессии и межпеременных связей с использованием стратегии поочередной оптимизации. Это позволяет снизить влияние шума градиентов и улучшить точность прогнозирования на длинных горизонтах. Не является ли разработка эффективных стратегий оптимизации, а не усложнение архитектур, ключевым фактором прогресса в области многомерного прогнозирования временных рядов?

Математическая Элегантность Временных Рядов: Вызовы и Ограничения

Традиционные модели временных рядов, такие как авторегрессия, зачастую оказываются неспособны адекватно отразить сложные взаимосвязи между различными переменными. Эти модели, полагающиеся на прошлые значения одной и той же переменной для прогнозирования будущего, игнорируют влияние других, потенциально важных факторов. В результате, при наличии значительных перекрестных зависимостей, точность прогнозов существенно снижается. Например, при прогнозировании продаж определенного товара, авторегрессионная модель может упустить взаимосвязь с ценами на сырье, рекламными кампаниями или даже погодными условиями, что приведет к неточным результатам и, как следствие, к неоптимальным решениям в области планирования и управления ресурсами.

Реальные временные ряды, будь то финансовые показатели, климатические данные или показатели активности нейронов, редко существуют в изоляции. Их динамика обусловлена сложным переплетением взаимосвязей между различными переменными, что делает традиционные методы анализа, ориентированные на одиночные ряды, недостаточно эффективными. Появляется необходимость в моделях, способных улавливать эти скрытые зависимости и учитывать их влияние на будущие значения. Современные исследования направлены на разработку алгоритмов, которые не просто прогнозируют развитие одного временного ряда, но и учитывают изменения в других связанных рядах, что позволяет создавать более точные и реалистичные прогнозы, отражающие истинную сложность окружающего мира. Такой подход особенно важен в системах, где даже незначительные изменения в одной переменной могут привести к каскадным эффектам во всей системе.

Несмотря на свою мощь, современные методы глубокого обучения часто сталкиваются с трудностями оптимизации при работе со сложными зависимостями во временных рядах. Проблема заключается в том, что при увеличении числа взаимосвязанных переменных и нелинейных взаимодействий, градиенты, используемые для обучения нейронных сетей, могут затухать или взрываться, что приводит к замедлению сходимости или даже к нестабильности процесса обучения. Это требует использования более сложных методов оптимизации, таких как адаптивные алгоритмы или регуляризация, а также тщательной настройки гиперпараметров, что значительно увеличивает вычислительные затраты и время, необходимые для получения надежных прогнозов. Более того, сложность ландшафта функции потерь, обусловленная этими зависимостями, может приводить к застреванию в локальных минимумах, препятствуя достижению глобального оптимума и снижая точность прогнозирования.

Ограничения существующих подходов в анализе временных рядов подчеркивают настоятельную необходимость разработки инновационных архитектур, которые целенаправленно решают проблему моделирования зависимостей. Традиционные методы часто не способны улавливать сложные взаимосвязи между переменными, что приводит к снижению точности прогнозов. Новые архитектуры должны быть способны эффективно представлять и использовать эти зависимости, чтобы добиться более надежных и точных результатов. В частности, важно создавать модели, которые могут учитывать нелинейные и долгосрочные зависимости, а также адаптироваться к изменяющимся условиям. Подобные разработки позволят значительно улучшить качество прогнозирования в различных областях, от финансов и экономики до метеорологии и инженерии.

Совместное обучение моделей авторегрессии (AR) и условной регрессии (CR) демонстрирует стабильную дисперсию градиентов на семи различных наборах данных при длине предсказания, равной 192.

AltTS: Декомпозиция Зависимостей для Эффективного Моделирования

AltTS использует двухпутевую архитектуру, разделяющую моделирование зависимостей во временных рядах от процесса оптимизации. Традиционно, эти этапы тесно связаны, что приводит к сложностям при обучении глубоких моделей. В AltTS, моделирование зависимостей выполняется в одном пути, генерируя признаки, которые затем используются для обучения основной модели во втором пути. Это разделение позволяет оптимизировать каждый этап независимо, что повышает эффективность обучения и снижает вычислительные затраты. Такой подход позволяет более эффективно использовать градиенты и избегать их «запутывания», характерного для традиционных методов, и, как следствие, ускоряет сходимость модели.

В процессе обучения глубоких моделей временных рядов часто возникает проблема запутанности градиентов (gradient entanglement), когда градиенты, относящиеся к разным этапам обработки, смешиваются и затрудняют эффективную оптимизацию. AltTS решает эту проблему, разделяя моделирование зависимостей во временных рядах и процесс оптимизации. Такое разделение позволяет более точно вычислять градиенты для каждого этапа, предотвращая их смешение и обеспечивая более стабильное и быстрое обучение модели. Это достигается за счет того, что моделирование зависимостей выполняется независимо от шагов оптимизации, что упрощает процесс обратного распространения ошибки и улучшает сходимость алгоритма.

Архитектура AltTS расширяет возможности существующих моделей, таких как channel independent и channel mix, обеспечивая более гибкий и мощный подход к моделированию зависимостей во временных рядах. В отличие от этих методов, которые часто ограничиваются фиксированными схемами взаимодействия между каналами, AltTS позволяет динамически адаптировать способ учета зависимостей в процессе обучения. Это достигается за счет введения дуального пути, где моделирование зависимостей отделено от процесса оптимизации, что позволяет более эффективно использовать вычислительные ресурсы и улучшить качество обучения, особенно при работе со сложными и многомерными временными рядами. Фактически, AltTS предоставляет обобщенную структуру, в рамках которой можно реализовать различные стратегии моделирования зависимостей, включая те, которые используются в channel independent и channel mix моделях, но с повышенной гибкостью и эффективностью.

Для повышения способности к захвату сложных динамик временных рядов, AltTS использует механизмы самовнимания переменного уровня (variable-level self-attention) и обратимую нормализацию экземпляров (reversible instance normalization). Само внимание переменного уровня позволяет модели динамически адаптировать область внимания к различным уровням временных зависимостей, что улучшает способность к моделированию долгосрочных связей. Обратимая нормализация экземпляров, в свою очередь, обеспечивает стабильность градиентов при обучении глубоких моделей, предотвращая проблему исчезающих или взрывающихся градиентов, что особенно важно для обработки длинных последовательностей временных рядов. Комбинация этих техник позволяет AltTS эффективно моделировать сложные паттерны и зависимости во временных данных.

Более высокая дисперсия градиентов AR/CR при совместном обучении на семи наборах данных указывает на нестабильность процесса, что обуславливает необходимость использования чередующейся оптимизации в AltTS.

Оптимизация AltTS: Гармония Алгоритмов и Точность Прогнозирования

AltTS использует возможности проверенных алгоритмов оптимизации, таких как Adam Optimizer, AMSGrad Optimizer и Block-Coordinate Descent, для повышения эффективности обучения. Adam Optimizer, благодаря адаптивности скорости обучения, ускоряет сходимость на различных задачах анализа временных рядов. AMSGrad Optimizer, являясь улучшением Adam, обеспечивает более стабильное обучение, особенно в задачах с невыпуклыми функциями потерь. Block-Coordinate Descent, в свою очередь, эффективно решает задачи оптимизации больших объемов данных, разбивая их на более мелкие подзадачи и оптимизируя их последовательно. Интеграция этих алгоритмов позволяет AltTS адаптироваться к различным характеристикам данных и требованиям к производительности.

В AltTS для упрощения процесса обучения используются методы итеративного развертывания алгоритмов и дифференцируемые слои оптимизации. Итеративное развертывание позволяет разложить сложный алгоритм оптимизации на последовательность более простых шагов, что облегчает его анализ и оптимизацию. Дифференцируемые слои оптимизации, в свою очередь, позволяют интегрировать процесс оптимизации непосредственно в структуру нейронной сети, делая его частью прямого прохода и обеспечивая возможность вычисления градиентов для оптимизации параметров как самой модели, так и алгоритма оптимизации. Это позволяет реализовать более эффективные и гибкие стратегии обучения, а также автоматизировать процесс настройки гиперпараметров оптимизатора.

Алгоритм Alternating Direction Method of Multipliers (ADMM) используется в AltTS для решения задач оптимизации с ограничениями, часто возникающих при анализе сложных временных рядов. ADMM позволяет декомпозировать исходную задачу на более простые подзадачи, которые решаются итеративно, что значительно упрощает процесс обучения и повышает сходимость. В контексте временных рядов, ограничения могут включать требования к гладкости, диапазону значений или другим специфическим характеристикам данных. Использование ADMM обеспечивает эффективное удовлетворение этих ограничений при минимизации целевой функции, что приводит к более точным и надежным результатам прогнозирования.

Методы разреженного моделирования, в сочетании с применением патчинга, значительно повышают эффективность и масштабируемость модели AltTS при работе с большими наборами данных временных рядов. Разреженное моделирование позволяет снизить вычислительную сложность за счет идентификации и исключения несущественных параметров или признаков, что приводит к уменьшению объема вычислений и требований к памяти. Патчинг, в свою очередь, разбивает входные данные на более мелкие фрагменты, обрабатываемые независимо, что позволяет распараллелить вычисления и ускорить процесс обучения, особенно на аппаратных платформах с ограниченными ресурсами. Комбинация этих техник обеспечивает возможность эффективной обработки и анализа больших объемов данных временных рядов, сохраняя при этом высокую точность прогнозирования.

Анализ дисперсии градиентов AR/CR показывает, что совместное обучение обеспечивает более стабильные градиенты по сравнению с поочередным обучением на семи наборах данных при длине прогноза 96, что подтверждается вычислением скользящей дисперсии градиентов для каждого параметра и суммированием по параметрам в каждом направлении.

Влияние и Перспективы Развития Прогнозирования Временных Рядов

Представленная модель AltTS демонстрирует значительный прогресс в области прогнозирования временных рядов, достигая передовых результатов или занимая второе место в большинстве оценочных сценариев на семи различных бенчмарках. Данное достижение указывает на высокую эффективность и надежность предложенного подхода в решении задач прогнозирования, охватывающих широкий спектр данных и горизонтов планирования. В ходе сравнительного анализа с существующими методами, AltTS последовательно демонстрирует превосходство, подтверждая свою способность эффективно моделировать сложные зависимости во временных рядах и предоставлять точные прогнозы, что делает её ценным инструментом для специалистов, работающих с данными, изменяющимися во времени.

Архитектура AltTS, отличающаяся разделением функциональных блоков, предоставляет уникальную гибкость для интеграции передовых методов моделирования зависимостей и оптимизационных алгоритмов. Такой подход позволяет исследователям и разработчикам легко экспериментировать с различными подходами к выявлению сложных взаимосвязей во временных рядах, не затрагивая при этом стабильность и эффективность основной системы. Благодаря модульной структуре, в AltTS можно внедрять новые алгоритмы, направленные на улучшение прогнозирования, или адаптировать существующие для решения специфических задач. Это делает AltTS не просто эффективным инструментом для прогнозирования, но и перспективной платформой для дальнейших исследований в области анализа временных рядов и машинного обучения.

Результаты всестороннего тестирования демонстрируют выдающуюся устойчивость и обобщающую способность разработанной системы AltTS. В ходе оценки на множестве эталонных наборов данных, система показала попадание в топ-2 лучших моделей в 49 из 56 случаев, что свидетельствует о её способности эффективно адаптироваться к различным типам временных рядов и условиям прогнозирования. Такой высокий уровень стабильности и надежности делает AltTS перспективным инструментом для решения широкого спектра задач, требующих точного прогнозирования временных зависимостей, и значительно превосходит по этому показателю многие существующие аналоги, такие как OLinear и PatchTST.

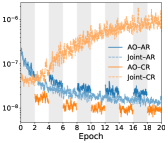
В ходе анализа данных на наборе ETTh1 с горизонтом прогнозирования в 720 временных шагов, разработанный фреймворк AltTS продемонстрировал значительное превосходство в точности. Среднеквадратичная ошибка (MSE) составила 0.435/0.453, что существенно ниже, чем при использовании традиционного подхода совместного обучения, где аналогичный показатель достигал значений 0.510/0.506. Данное улучшение свидетельствует о высокой эффективности декомпозированной архитектуры AltTS в улавливании сложных временных зависимостей и повышении точности долгосрочного прогнозирования, особенно в задачах, связанных с анализом многомерных временных рядов.

В ходе сравнительного анализа с базовыми моделями, разработанная система AltTS продемонстрировала выдающиеся результаты, достигнув точности в Top-2 в 49 из 56 оценочных сценариев. Это значительно превосходит показатели OLinear, набравшей всего 25 баллов, и PatchTST, достигшей 19 баллов. Такое существенное превосходство подтверждает эффективность архитектуры AltTS и её способность к обобщению данных, что делает её перспективным инструментом для решения широкого спектра задач прогнозирования временных рядов и открывает возможности для дальнейших исследований в области повышения её производительности и адаптации к различным типам данных.

Дальнейшие исследования AltTS направлены на расширение возможностей обработки еще более сложных временных рядов, включая данные с нелинейными зависимостями и значительным уровнем шума. Особое внимание уделяется адаптации фреймворка к задачам прогнозирования в различных областях, таких как финансы, где точные прогнозы могут существенно повлиять на инвестиционные стратегии; здравоохранение, где прогнозирование эпидемий или потребности в медицинских ресурсах имеет жизненно важное значение; и мониторинг окружающей среды, где своевременное обнаружение изменений климата или загрязнения позволяет принимать эффективные меры. Предполагается, что расширение архитектуры и алгоритмов оптимизации позволит AltTS успешно применяться для решения широкого спектра практических задач, требующих высокой точности и надежности прогнозов временных рядов.

Представленная работа демонстрирует стремление к математической точности в прогнозировании многомерных временных рядов. Разработанный фреймворк AltTS, разделяя авторегрессивные и межпеременные зависимости, нацелен на решение проблемы запутанности градиентов, что особенно важно для долгосрочных прогнозов. Грейс Хоппер однажды заметила: «Лучший способ программировать — это программировать». Этот принцип находит отражение в AltTS, где тщательное разделение и оптимизация отдельных компонентов алгоритма позволяют добиться более стабильных и предсказуемых результатов. В конечном счете, фокус на детерминированности и воспроизводимости результатов, как и в предложенной архитектуре, является ключевым для создания надежных и эффективных систем.

Что дальше?

Представленная работа, безусловно, демонстрирует потенциал разделения авторегрессионных и межпеременных зависимостей для улучшения прогнозирования многомерных временных рядов. Однако, стоит признать, что элегантность решения не гарантирует его универсальности. Альтернативная оптимизация, хоть и смягчает проблему «запутанности градиентов», не устраняет её полностью — это скорее прагматичный компромисс, чем фундаментальное решение. Вопрос о доказательной гарантии сходимости алгоритма остается открытым, а эмпирическая проверка на ограниченном наборе данных не может служить абсолютным оправданием.

Будущие исследования должны быть направлены на разработку теоретически обоснованных методов, способных гарантированно избегать локальных минимумов и обеспечивать устойчивое обучение в долгосрочной перспективе. Особый интерес представляет поиск способов формализации и учета нелинейных взаимодействий между переменными, а также разработка метрик для оценки качества прогнозирования на горизонте, достаточном для выявления истинных закономерностей, а не просто подгонки к историческим данным. Эвристики, какими бы полезными они ни казались, всегда должны подвергаться строгому математическому анализу.

В конечном итоге, истинный прогресс в области прогнозирования временных рядов требует не просто улучшения существующих моделей, но и переосмысления самой концепции «прогноза» — признания того, что будущее, по своей природе, неопределенно, а любое предсказание — это лишь вероятностная оценка, а не абсолютная истина. И в этом заключается настоящая сложность, и, возможно, непреодолимое ограничение любой модели.

Оригинал статьи: https://arxiv.org/pdf/2602.11533.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-14 02:21