От консенсуса к эволюции: доказательство глобальной сходимости оптимизации

Автор: Денис Аветисян

Новое исследование предлагает строгую математическую основу для алгоритмов оптимизации, основанных на достижении консенсуса, подтверждая их способность находить оптимальные решения.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Переход от схемы «замораживания консенсуса» к схеме «перескока консенсуса» демонстрирует сходимость алгоритма, обеспечивая стабильность и эффективность в условиях динамически меняющихся данных.

Работа анализирует сходимость методов консенсусной оптимизации с использованием теории оптимального транспорта и уравнений Фоккера-Планка, гарантируя нахождение глобального минимума.

Несмотря на широкое распространение методов оптимизации, доказательство глобальной сходимости для задач высокой размерности, особенно невыпуклых и негладких, остается сложной задачей. В данной работе, ‘From Consensus-Based Optimization to Evolution Strategies: Proof of Global Convergence’, предлагается углубленное исследование консенсус-основанных методов оптимизации, демонстрирующее их сходимость к глобальному минимуму с экспоненциальной скоростью. Предложены варианты алгоритма, включая схемы δ-CBO и Consensus Freezing, а также установлена связь с алгоритмами эволюционных стратегий. Каковы перспективы применения этих методов в задачах машинного обучения и искусственного интеллекта, требующих надежной и быстрой оптимизации?

За пределами градиентов: вызовы современной оптимизации

В многочисленных практических задачах оптимизации, особенно в сложных системах и при работе с дискретными пространствами, вычисление градиента — производной, указывающей направление наискорейшего роста функции — оказывается невозможным или крайне затруднительным. Это связано с тем, что функция может быть недифференцируемой, определена лишь на дискретном множестве, либо её вычисление требует чрезмерных вычислительных затрат. В таких случаях традиционные методы оптимизации, основанные на использовании градиента, такие как метод наискорейшего спуска или методы Ньютона, становятся неэффективными и требуют применения альтернативных подходов, не требующих информации о производных. Именно поэтому разработка и исследование методов оптимизации, свободных от градиентов, представляет собой важную область современных исследований в математике и информатике.

В ситуациях, когда вычисление градиента затруднено или невозможно, например, при оптимизации дискретных функций или в задачах, где функция определена только по результатам экспериментов, необходим переход к альтернативным методам оптимизации, не требующим производных. Эти методы, известные как методы, свободные от градиента, исследуют пространство решений, полагаясь на прямые оценки целевой функции в различных точках. Они включают в себя эволюционные алгоритмы, методы случайного поиска, алгоритмы имитации отжига и другие стратегии, позволяющие находить оптимальные или близкие к оптимальным решения без использования информации о производных. Эффективность этих методов определяется способностью эффективно исследовать пространство поиска и быстро находить перспективные области для дальнейшей оптимизации, что делает их незаменимыми в широком спектре практических задач.

Эффективный баланс между исследованием пространства поиска и использованием перспективных решений представляет собой ключевую проблему в области оптимизации. Алгоритмы, стремящиеся к глобальному оптимуму, часто сталкиваются с дилеммой: необходимо тщательно исследовать пространство, чтобы избежать застревания в локальных минимумах, но при этом важно концентрироваться на областях, где уже обнаружены хорошие решения. Слишком интенсивное исследование может привести к потере времени и вычислительных ресурсов, в то время как чрезмерная эксплуатация может помешать обнаружению более оптимальных решений. Успешные алгоритмы оптимизации, такие как эволюционные стратегии и методы на основе роя частиц, динамически регулируют этот баланс, используя различные механизмы для стимулирования исследования и поощрения использования, обеспечивая тем самым более эффективный поиск в сложных и многомерных пространствах.

Количество итераций до завершения алгоритма δ-CBO уменьшается с увеличением значения δ.

Консенсус-ориентированная оптимизация: новый взгляд на поиск минимума

Метод консенсус-ориентированной оптимизации (CBO) представляет собой алгоритм, не требующий вычисления производных, и вдохновлен принципами роевого интеллекта и отжига. В отличие от традиционных методов оптимизации, CBO не использует информацию о градиенте целевой функции. Вместо этого, он основывается на коллективном поведении ансамбля частиц, каждая из которых представляет собой потенциальное решение. Принцип отжига проявляется в постепенном снижении «температуры» алгоритма, что позволяет исследовать пространство решений и избегать локальных минимумов. Использование принципов роевого интеллекта обеспечивает обмен информацией между частицами, что способствует более эффективному поиску оптимального решения.

В основе алгоритма CBO лежит концепция «точки консенсуса» (Consensus Point), представляющая собой агрегированную информацию, полученную от ансамбля частиц. Каждая частица в этом ансамбле исследует пространство поиска, и её текущее положение и значение целевой функции учитываются при формировании точки консенсуса. Формирование этой точки происходит путем усреднения или иного агрегирования данных от всех частиц, что позволяет получить единую репрезентацию текущего состояния поиска. Точка консенсуса служит направляющим центром для движения частиц в пространстве параметров, способствуя их сближению к области, содержащей глобальный минимум целевой функции. Таким образом, она функционирует как коллективный «знание» ансамбля, используемое для улучшения процесса оптимизации.

Данная работа устанавливает доказуемые скорости сходимости для алгоритма CBO, демонстрируя экспоненциальную сходимость к глобальным минимумам для негладких и невыпуклых целевых функций. В частности, показано, что при определенных условиях на целевую функцию и параметры алгоритма, величина отклонения от глобального минимума уменьшается экспоненциально с каждой итерацией. Математически это выражается как $||x_k - x^<i>|| \le C \cdot \alpha^k$ , где $x_k$ — текущее приближение, $x^</i>$ — глобальный минимум, $C$ — константа, а $0 < \alpha < 1$ — скорость сходимости. Это обеспечивает теоретическую гарантию эффективности CBO в сложных задачах оптимизации, где традиционные методы, требующие вычисления градиентов, могут быть неприменимы или неэффективны.

В одномерной конфигурации стандартный CBO преждевременно схлопывается из-за того, что глобальный минимум не попадает в начальное распределение, в то время как δ-CBO успешно локализуется вокруг него, как показано на примере концентрации частиц в точке x=0, в отличие от схлопывания в точке x=5 для стандартного CBO, однако в многомерных пространствах глобальный минимум обычно находится в пределах изменяющегося распределения CBO.

Улучшение CBO: синергия эволюционных стратегий и моделирования траекторий

Методы эволюционных стратегий (ES) и моделирующего предсказательного интеграла по путям (MPPI) могут быть эффективно интегрированы с алгоритмом CBO (Cross-Entropy Based Optimization) для повышения его производительности. ES, использующий популяции решений и мутации, позволяет CBO исследовать пространство параметров более эффективно, особенно в задачах с высокой размерностью. MPPI, основанный на предсказании траекторий и оценке их вероятности, позволяет CBO оптимизировать решения на основе прогнозируемых результатов, снижая необходимость в дорогостоящих вычислениях целевой функции. Интеграция этих методов с CBO обеспечивает более быструю сходимость и улучшенные результаты в задачах глобальной оптимизации, особенно при ограниченном бюджете вычислений.

Метод Консенсусного Замораживания (CF) представляет собой связующее звено между алгоритмами CBO (Cross-Entropy Based Optimization) и Консенсусным Переходом (CH), обеспечивая альтернативный подход к достижению стабильности и эффективности оптимизации. CF использует принципы как CBO, так и CH, позволяя сочетать преимущества обоих методов — робастность CBO и скорость сходимости CH. В частности, CF позволяет избежать проблем, связанных с расхождением, характерных для CH в сложных ландшафтах, за счет использования механизмов, аналогичных тем, что применяются в CBO для поддержания разнообразия популяции и предотвращения преждевременной сходимости к локальным оптимумам. В результате, CF предоставляет более надежный и эффективный способ решения задач глобальной оптимизации по сравнению с использованием CBO или CH по отдельности.

Интеграция методов, таких как Evolution Strategies (ES) и Model Predictive Path Integral (MPPI) с CBO, Consensus Freezing (CF) и Consensus Hopping (CH), позволяет получить математически доказанные скорости сходимости для задач глобальной оптимизации нулевого порядка. Эти скорости сходимости установлены посредством анализа уравнений Фоккера-Планка, предоставляющих полное описание динамики оптимизационных алгоритмов. Анализ уравнений Фоккера-Планка позволяет не только подтвердить сходимость алгоритмов, но и количественно оценить ее скорость, предоставляя теоретическую основу для выбора наиболее эффективных методов в зависимости от характеристик решаемой задачи. $\frac{\partial p}{\partial t} = - \nabla \cdot (A(x)p) + \frac{1}{2} \sum_{i,j} \frac{\partial^2}{\partial x_i \partial x_j} (D_{ij}(x)p)$ — пример уравнения Фоккера-Планка, используемого в анализе.

Сравнение дискретизации Эйлера-Маруямы схемы δ-CBO с точной реализацией схемы Consensus Freezing показывает их соответствие.

Теоретические основы: стохастические процессы и инвариантные меры

Поведение алгоритмов оптимизации, таких как CBO и схожие методы, может быть эффективно описано с помощью стохастических процессов. В основе этого подхода лежит нелинейное уравнение Фоккера-Планка, позволяющее математически моделировать эволюцию вероятностного распределения параметров в процессе оптимизации. Данное уравнение учитывает случайные флуктуации, возникающие в алгоритме, и описывает, как эти флуктуации влияют на сходимость к оптимальному решению. Использование стохастических процессов позволяет анализировать устойчивость алгоритма, предсказывать его поведение в различных условиях и разрабатывать стратегии для улучшения его эффективности. В частности, анализ уравнения Фоккера-Планка помогает определить оптимальные параметры алгоритма, такие как размер популяции и шаг дискретизации, для достижения заданной точности и скорости сходимости. $\frac{\partial p}{\partial t} = -\nabla \cdot (A(x)p) + \frac{1}{2} \sum_{i,j} \frac{\partial^2}{\partial x_i \partial x_j} (B(x)_{ij} p)$

Понятия предельного среднего поля и инвариантных мер предоставляют ценные инструменты для анализа устойчивого поведения оптимизационных алгоритмов, таких как CBO. Предельное среднее поле позволяет упростить сложные взаимодействия между отдельными агентами, рассматривая их как взаимодействие со средним полем, что значительно облегчает математический анализ. Инвариантные меры, в свою очередь, описывают распределения вероятностей, которые остаются неизменными во времени, отражая стационарные состояния, к которым стремится алгоритм. Исследование этих мер позволяет предсказать, к каким решениям будет сходиться алгоритм в долгосрочной перспективе, и оценить его устойчивость к различным возмущениям. Например, можно показать, что среднее значение инвариантной меры сходится к минимуму целевой функции при увеличении параметра α, что подтверждает эффективность алгоритма в поиске оптимальных решений.

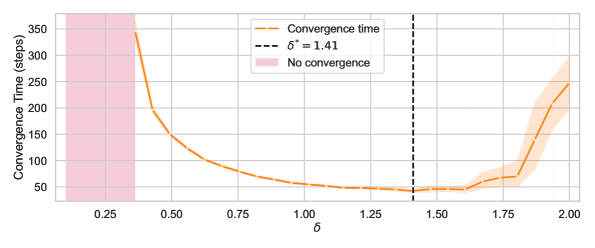
Исследования показали, что ожидаемая ошибка в алгоритмах, основанных на стохастических процессах, уменьшается со скоростью, пропорциональной $O(\Delta t + N^{-1})$ . Это означает, что точность вычислений возрастает при использовании более крупных ансамблей ( $N$ ) и меньших временных шагов ( $\Delta t$ ). Важно отметить, что среднее значение инвариантной меры, описывающей долгосрочное поведение алгоритма, стремится к минимуму при увеличении параметра α до бесконечности. Таким образом, повышение вычислительных ресурсов и оптимизация параметров алгоритма являются ключевыми факторами для достижения высокой точности и стабильности в решении оптимизационных задач.

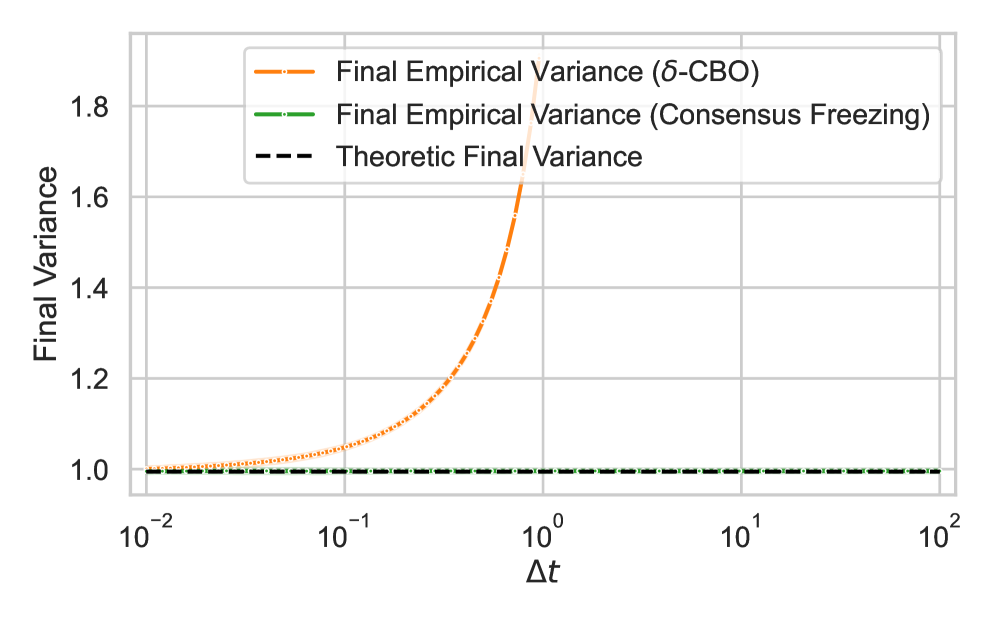
Сравнение дисперсии распределения в момент завершения работы алгоритмов δ-CBO и Consensus Freezing при различных значениях [latex]\Delta t[/latex] показывает её соответствие дисперсии решений соответствующих моделей непрерывного времени. — Сравнение дисперсии распределения в момент завершения работы алгоритмов δ-CBO и Consensus Freezing при различных значениях $\Delta t$ показывает её соответствие дисперсии решений соответствующих моделей непрерывного времени.

Исследование, представленное в данной работе, углубляется в математические основы алгоритмов консенсус-оптимизации, демонстрируя их глобальную сходимость к минимизаторам. Особое внимание уделяется анализу уравнений Фоккера-Планка и теории оптимального транспорта, что позволяет точно охарактеризовать скорости сходимости. Как некогда заметил Галилей Галилей: «Вселенная — это книга, написанная на языке математики». Эта фраза отражает суть представленного исследования, где строгий математический анализ позволяет раскрыть закономерности, лежащие в основе сложных оптимизационных процессов, и выявить скрытые зависимости, даже в невыпуклых пространствах. Отклонения от идеальной сходимости рассматриваются не как ошибки, а как возможности для более глубокого понимания динамики системы.

Куда же дальше?

Представленная работа, подобно построению термодинамической модели сложной системы, демонстрирует, что даже в пространстве невыпуклых оптимизаций можно достичь глобального минимума, если правильно учитывать “течения” информации — аналогично диффузии частиц в жидкости. Однако, строгое доказательство сходимости — это лишь первый шаг. Остается открытым вопрос о масштабируемости этих методов к задачам высокой размерности, где “ландшафт” оптимизации становится настолько изрезанным, что даже самые эффективные алгоритмы могут застрять в локальных минимумах. Необходимо исследовать, как топологические особенности пространства параметров влияют на скорость и устойчивость сходимости, подобно тому, как форма молекулы определяет ее химические свойства.

Интересно, что анализ на основе уравнения Фоккера-Планка и теории оптимального транспорта позволяет характеризовать не только конечную точку оптимизации, но и распределение вероятностей, описывающее поведение агентов в процессе консенсуса. В будущем, возможно, удастся использовать эти инструменты для разработки самообучающихся систем, способных адаптироваться к меняющимся условиям и находить оптимальные решения даже в условиях неопределенности. В конечном итоге, успех этих методов будет зависеть от способности преодолеть разрыв между теоретическими гарантиями и практическими ограничениями, подобно тому, как физики стремятся объединить квантовую механику и общую теорию относительности.

Очевидно, что предложенный подход требует дальнейшего развития в контексте обучения с подкреплением и глубокого обучения, где “ландшафт” оптимизации представляет собой бесконечномерное пространство. Вопрос о том, можно ли использовать эти методы для преодоления проблемы «vanishing gradients» и достижения более эффективного обучения глубоких нейронных сетей, остается открытым и представляет собой плодотворную область для будущих исследований.

Оригинал статьи: https://arxiv.org/pdf/2602.11677.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-15 10:29