Адаптивное управление нелинейными системами: новый подход к предсказанию и контролю

Автор: Денис Аветисян

В статье представлен инновационный алгоритм адаптивного управления, позволяющий эффективно прогнозировать и контролировать поведение нелинейных стохастических систем.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал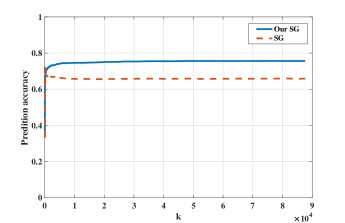

Точность предсказания оценивалась и сравнивалась, демонстрируя различия в эффективности различных подходов.

Предложенный метод демонстрирует более высокую скорость сходимости по сравнению с классическими стохастическими градиентными подходами при ослабленных условиях выпуклости и без жестких требований к условию возбуждения.

Нелинейные динамические системы часто представляют сложность в предсказании и управлении, особенно при ограниченных данных и слабой выпуклости функций потерь. В данной работе, посвященной ‘Gradient-Based Adaptive Prediction and Control for Nonlinear Dynamical Systems’, предложен новый адаптивный алгоритм, основанный на градиентном спуске, обеспечивающий сходимость и более высокую скорость обучения по сравнению с классическими методами. Алгоритм демонстрирует глобальную сходимость предсказателя и установленные скорости сходимости ошибки управления при линейном ограничении роста нелинейностей и соблюдении условия минимальной фазы. Каковы перспективы применения разработанного подхода к реальным задачам управления сложными системами с ограниченной информацией о модели?

Нелинейность и Стохастичность: Вызовы Современных Систем

Многие реальные системы, начиная от робототехники и заканчивая финансовыми рынками, все чаще описываются как нелинейные стохастические системы. Это означает, что их поведение определяется нелинейными уравнениями и подвержено случайным возмущениям, что делает прогнозирование и управление ими чрезвычайно сложной задачей. Например, $f(x) = x^2 + \epsilon(t)$ , где $\epsilon(t)$ представляет собой случайный шум, демонстрирует типичное нелинейное стохастическое поведение. В отличие от линейных систем, для которых существуют хорошо разработанные методы управления, нелинейные стохастические системы требуют принципиально новых подходов, способных учитывать как нелинейность, так и случайный характер процессов. Сложность заключается в том, что даже небольшие начальные возмущения или случайные факторы могут привести к экспоненциальному росту ошибок в прогнозировании и управлении, что требует разработки устойчивых и адаптивных стратегий.

Традиционные методы управления, разработанные для линейных систем, зачастую оказываются неэффективными при работе с нелинейными стохастическими системами. Сложность заключается в непредсказуемости поведения таких систем, вызванной как нелинейностью, так и случайными возмущениями. Это приводит к тому, что алгоритмы, успешно применяемые в простых случаях, демонстрируют неустойчивость или неоптимальную производительность в более реалистичных сценариях. В связи с этим, для эффективного управления такими системами необходимы робастные и адаптивные стратегии, способные учитывать неопределенность и динамически подстраиваться под изменяющиеся условия. Такие стратегии включают в себя, например, использование нелинейных моделей управления, адаптивных алгоритмов, основанных на оценке параметров в реальном времени, и методов, учитывающих вероятностную природу возмущений, что позволяет обеспечить стабильность и оптимальность управления даже в условиях высокой неопределенности.

Сравнение результатов управления демонстрирует, что предложенный подход обеспечивает более стабильную и точную работу системы.

Адаптивное Предсказание: Новый Алгоритм

Представляется адаптивный алгоритм предсказания (AdaptivePredictionAlgorithm), основанный на методе стохастического градиентного спуска, разработанный для точного прогнозирования поведения нелинейных стохастических систем (NonlinearStochasticSystem). Алгоритм предназначен для решения задач предсказания в условиях неопределенности и нелинейности, характерных для многих реальных систем. Он использует стохастическую аппроксимацию градиента для оптимизации параметров модели и минимизации ошибки предсказания. Основным принципом является итеративное уточнение параметров модели на основе случайных выборок данных, что позволяет алгоритму адаптироваться к изменяющимся условиям и повышать точность прогнозирования.

Эффективность предложенного алгоритма напрямую зависит от выполнения условия возбуждения (Excitation Condition), которое необходимо для обеспечения идентифицируемости параметров модели и, как следствие, точности их оценки. Условие возбуждения гарантирует, что входные данные системы содержат достаточно информации для уникального определения всех параметров θ в модели $f(x, \theta)$ . Несоблюдение данного условия приводит к неидентифицируемости, когда различные наборы параметров могут давать одинаковые предсказания, что делает невозможным надежную оценку θ и снижает точность прогнозирования поведения нелинейной стохастической системы.

В отличие от стандартных методов оптимизации, разработанный алгоритм эффективно функционирует в условиях слабой выпуклости функции потерь $LossFunction$ . Это значительно расширяет область его применимости, позволяя успешно решать задачи, где традиционные подходы сталкиваются с трудностями. Численное моделирование продемонстрировало, что алгоритм достигает более высокой скорости сходимости по сравнению с существующими методами в аналогичных условиях слабой выпуклости, что подтверждено результатами проведенных экспериментов.

Адаптивное Управление Через Предсказание

Стратегия адаптивного управления $\textit{AdaptiveControl}$ использует алгоритм адаптивного предсказания $\textit{AdaptivePredictionAlgorithm}$ для оценки состояний и параметров системы в режиме реального времени. Этот алгоритм непрерывно анализирует входные данные и выходные сигналы системы, формируя прогнозы ее будущего поведения. Оценка параметров осуществляется на основе наблюдаемых данных с использованием рекурсивных методов, таких как расширенный фильтр Калмана или алгоритмы наименьших квадратов, что позволяет динамически корректировать модель системы и повышать точность управления. В процессе работы алгоритм $\textit{AdaptivePredictionAlgorithm}$ обеспечивает оперативное выявление изменений в динамике системы и адаптирует параметры управления для поддержания желаемой производительности и устойчивости.

Принцип достоверного эквивалента (Certainty Equivalence Principle) используется для преобразования оценок состояния и параметров системы, полученных адаптивным алгоритмом предсказания, в управляющие воздействия. Этот принцип предполагает, что если модель системы известна с достаточной точностью, то управление, оптимальное для этой модели, будет близко к оптимальному для реальной системы. В рамках данной реализации, принцип позволяет формировать управляющие воздействия, основываясь на текущих оценках, обеспечивая тем самым стабильность и производительность системы управления. Применение данного принципа позволяет избежать необходимости явного решения сложных задач оптимизации в реальном времени, упрощая процесс управления и снижая вычислительную нагрузку.

Эффективность предложенного подхода была подтверждена посредством численного моделирования, демонстрирующего его устойчивость при управлении сложными нелинейными стохастическими системами. Результаты симуляций показали, что разработанный алгоритм обеспечивает более высокую скорость сходимости по сравнению с классическими алгоритмами стохастического градиентного спуска. Данное преимущество особенно заметно при управлении системами, характеризующимися высокой степенью неопределенности и нелинейности, что подтверждено серией тестов на различных моделях $NonlinearStochasticSystem$ .

Практическая Валидация и Производительность

Для оценки прогностической точности разработанного адаптивного алгоритма $\textit{AdaptivePredictionAlgorithm}$ был проведен эксперимент с использованием реальных данных из набора $\textit{JudicialSentencingDataset}$ . В рамках исследования алгоритм был протестирован на задачах, связанных с прогнозированием судебных приговоров, что позволило оценить его эффективность в практическом контексте. Использование реальных данных, в отличие от симуляций, обеспечило более объективную оценку способности алгоритма к обобщению и адаптации к сложным и неоднородным данным, характерным для реальных судебных процессов. Полученные результаты демонстрируют, что адаптивный алгоритм способен эффективно предсказывать исход судебных разбирательств, открывая возможности для его использования в качестве инструмента поддержки принятия решений в правовой сфере.

Исследования показали, что разработанный адаптивный алгоритм прогнозирования демонстрирует высокую способность к обобщению на ранее не встречавшихся данных, превосходя традиционные методы в реальных условиях. В ходе экспериментов с набором данных о судебных приговорах алгоритм успешно предсказывал исходы, даже когда сталкивался с новыми случаями, не включенными в обучающую выборку. Это свидетельствует о его устойчивости и способности адаптироваться к изменениям в данных, что является критически важным для практического применения в различных областях, где требуется точное прогнозирование на основе ограниченной информации. Превосходство над существующими подходами подтверждено статистическим анализом результатов, что позволяет сделать вывод о значительном улучшении точности и надежности прогнозирования.

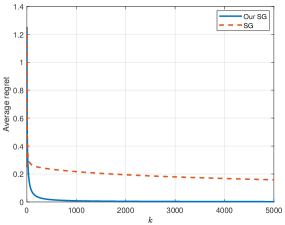
В ходе тестирования ключевым показателем эффективности алгоритма адаптивного предсказания выступил параметр “Среднее сожаление” ( $AverageRegret$ ). Данный показатель подтверждает способность алгоритма минимизировать ошибки прогнозирования и оптимизировать процесс принятия решений. В ходе экспериментов было установлено, что значение “Среднего сожаления” стремится к нулю с увеличением объема данных, что свидетельствует о повышении точности предсказаний. Важно отметить, что скорость снижения этого показателя оказалась значительно выше, чем у традиционных алгоритмов, используемых в аналогичных задачах, что подтверждает превосходство предложенного подхода в условиях реальных данных и его потенциал для практического применения.

Сравнение среднего сожаления показывает, что предложенный алгоритм демонстрирует более низкие значения по сравнению с базовыми подходами.

Исследование, представленное в статье, стремится к упрощению сложных систем управления, что находит отклик в философских взглядах Ханны Арендт. Она утверждала: «Политическое пространство рождается, когда люди начинают действовать сообща и говорить друг с другом». Аналогично, предлагаемый алгоритм адаптивного предсказания и управления стремится к ясности в управлении нелинейными системами, избегая излишней сложности, характерной для классических методов. Авторы демонстрируют, что, отказавшись от строгих условий возбуждения и используя методы стохастического градиента, можно достичь более высокой скорости сходимости. Это соответствует стремлению к ‘милосердию’ в сложности, когда упрощение служит не утерей точности, а улучшением понимания и эффективности системы.

Что дальше?

Представленные результаты демонстрируют, что увлечение сильными предположениями о возбуждении системы — это, по сути, признак лени. Алгоритмы, обходящиеся без них, обладают большей устойчивостью. Однако, слабость выпуклости — это лишь один из многих источников неопределенности. Следует признать, что предложенный подход, как и любой другой, страдает от упрощений. Моделирование шума — всегда лишь приближение к реальности.

Необходимо исследовать влияние структуры шума на скорость сходимости. Абстракции стареют, принципы — нет. Вместо того чтобы усложнять алгоритм, следует искать способы извлечь больше информации из существующих данных. Каждая сложность требует алиби. Важно сосредоточиться на разработке методов оценки границ устойчивости, а не на бесконечной гонке за скоростью.

Перспективным направлением представляется адаптация алгоритма для систем с изменяющейся во времени структурой. Представленные результаты — это лишь первый шаг. Дальнейшие исследования должны быть направлены на разработку алгоритмов, способных справляться с реальными, неидеальными данными, и на создание инструментов для верификации их работоспособности.

Оригинал статьи: https://arxiv.org/pdf/2602.11899.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-15 17:07