Оценка опционов: повышение точности с помощью современных методов моделирования

Автор: Денис Аветисян

В статье исследуются возможности повышения эффективности расчёта цен опционов и их чувствительности к изменениям рыночных факторов за счёт применения квази-Монте-Карло методов и глобального анализа чувствительности.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Наблюдается, что анализ азиатского опциона путём применения метода главных компонент (PCA) с размерностью D=32 позволяет оценить чувствительность цены опциона к изменениям базовых параметров, демонстрируя зависимость первого порядка [latex]S_i[/latex] и общую чувствительность [latex]S_i^{tot}[/latex] от варьируемой переменной [latex]i[/latex]. — Наблюдается, что анализ азиатского опциона путём применения метода главных компонент (PCA) с размерностью D=32 позволяет оценить чувствительность цены опциона к изменениям базовых параметров, демонстрируя зависимость первого порядка $S_i$ и общую чувствительность $S_i^{tot}$ от варьируемой переменной $i$ .

Исследование эффективности методов Монте-Карло, квази-Монте-Карло и дифференцирования для оценки финансовых деривативов и анализа их чувствительности.

Вычислительная сложность оценки производных финансовых инструментов и их чувствительностей представляет собой постоянную проблему в современной финансовой инженерии. В данной работе, ‘Application of Quasi Monte Carlo and Global Sensitivity Analysis to Option Pricing and Greeks’, исследуется применение методов квази-Монте-Карло и глобального анализа чувствительности для повышения эффективности расчетов цен и греков опционов. Показано, что квази-Монте-Карло превосходит стандартный Монте-Карло, особенно в задачах высокой размерности, а комбинирование с анализом чувствительности позволяет объяснить наблюдаемые улучшения в сходимости и точности. Возможно ли дальнейшее снижение вычислительных затрат и повышение надежности оценки рисков с помощью гибридных подходов и адаптивных стратегий выборки?

Элегантность Моделирования: Вызов Точности в Финансовых Расчётах

Оценка стоимости и рисков сложных финансовых инструментов требует применения надёжных вычислительных методов. Это обусловлено тем, что традиционные подходы часто сталкиваются с трудностями при моделировании нелинейных зависимостей и неопределенностей, характерных для финансовых рынков. Надёжные методы позволяют учитывать множество факторов, влияющих на стоимость, таких как процентные ставки, волатильность активов и корреляции между ними. $\sigma = \sqrt{\frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2 }$ Точность этих методов критически важна, поскольку даже незначительные ошибки в оценке могут привести к значительным финансовым потерям, особенно при работе с деривативами и другими сложными финансовыми продуктами. Поэтому разработка и применение передовых вычислительных техник является ключевым фактором для обеспечения стабильности и эффективности финансовых рынков.

Традиционные методы Монте-Карло, несмотря на свою универсальность в оценке стоимости и риска сложных финансовых инструментов, зачастую сталкиваются с проблемой медленной сходимости и высокой дисперсии результатов. Это означает, что для достижения приемлемой точности требуется проводить огромное количество симуляций, что значительно увеличивает вычислительные затраты и время моделирования. Высокая дисперсия, в свою очередь, приводит к тому, что полученные оценки могут сильно различаться при повторных запусках, что снижает надёжность прогнозов и затрудняет принятие обоснованных финансовых решений. В результате, даже при использовании мощных вычислительных ресурсов, стандартные методы Монте-Карло могут оказаться недостаточно эффективными для точной оценки сложных финансовых производных, особенно в условиях повышенной волатильности рынка.

Вычислительная нагрузка при построении финансовых моделей экспоненциально возрастает по мере усложнения самих моделей и повышения требуемой точности расчетов. Это связано с тем, что для оценки рисков и стоимости сложных финансовых инструментов часто требуются многомерные симуляции, включающие большое количество переменных и сценариев. Каждое увеличение числа переменных или стремление к более высокой точности приводит к геометрическому росту объема необходимых вычислений, что может потребовать значительных временных и аппаратных ресурсов. Например, для оценки стоимости опционов с экзотическими условиями или моделирования портфелей с большим количеством активов, традиционные методы могут оказаться неприменимыми из-за чрезмерной вычислительной сложности. В результате, повышение точности и детализации моделей часто сталкивается с практическими ограничениями, связанными с доступными вычислительными мощностями и временем, необходимым для получения результатов.

Сравнение времени вычислений показало, что при увеличении [latex]nn[/latex] количество базовых активов, автоматическое дифференцирование (AAD, синяя линия) значительно превосходит центральные конечные разности (красная линия) по скорости вычисления цены и всех греков азиатской опции, используя моделирование Монте-Карло с 200 000 сценариями. — Сравнение времени вычислений показало, что при увеличении $nn$ количество базовых активов, автоматическое дифференцирование (AAD, синяя линия) значительно превосходит центральные конечные разности (красная линия) по скорости вычисления цены и всех греков азиатской опции, используя моделирование Монте-Карло с 200 000 сценариями.

Совершенствование Симуляций: Методы Снижения Дисперсии

Методы снижения дисперсии направлены на уменьшение статистической ошибки в методах Монте-Карло, что позволяет достичь заданной точности при меньшем количестве случайных выборок. Традиционно, оценка точности в симуляциях Монте-Карло обратно пропорциональна квадратному корню из числа выборок. Снижение дисперсии, таким образом, эквивалентно увеличению эффективности симуляции, поскольку для достижения той же точности требуется значительно меньше вычислительных ресурсов. Это особенно важно в сложных моделях, где каждая симуляция может быть ресурсоемкой, и сокращение необходимого количества итераций приводит к существенной экономии времени и затрат.

Методы квази-Монте-Карло (КМК) представляют собой альтернативный подход к стандартным методам Монте-Карло, использующий последовательности с низкой расходимостью, такие как последовательности Соболя, для генерации более равномерно распределенных выборок. В отличие от псевдослучайных чисел, генерируемых стандартными методами Монте-Карло, последовательности с низкой расходимостью стремятся минимизировать пробелы и кластеризацию в пространстве выборок. Это достигается путем использования детерминированных алгоритмов, которые обеспечивают более равномерное заполнение пространства по сравнению со случайными числами, что приводит к снижению статистической погрешности и повышению эффективности моделирования.

Методы квази-Монте-Карло (QMC) обеспечивают ускорение сходимости и снижение вычислительных затрат по сравнению со стандартными методами Монте-Карло за счет улучшения свойств заполнения пространства выборкой. Вместо использования случайных чисел, QMC использует детерминированные низкодискрептные последовательности, такие как последовательности Соболя, которые равномернее распределены в многомерном пространстве. Это приводит к снижению статистической ошибки при той же численности выборки или достижению заданной точности с меньшим количеством сэмплов, что позволяет сократить вычислительные затраты до трех порядков величины (до 10³ раз) в определенных задачах.

Эффективность методов снижения дисперсии, таких как квази-Монте-Карло, напрямую зависит от так называемой “эффективной размерности” (EffectiveDimension) решаемой задачи. Под эффективной размерностью понимается количество параметров, существенно влияющих на результат моделирования. При низкой эффективной размерности (значительно меньше общего числа параметров) стандартные методы снижения дисперсии демонстрируют высокую эффективность. Однако, с ростом эффективной размерности, необходимо применять более сложные методы или комбинации методов для достижения приемлемой скорости сходимости и снижения вычислительных затрат. Оценка эффективной размерности является ключевым шагом при выборе оптимальной стратегии снижения дисперсии для конкретной задачи.

Сравнение различных методов Монте-Карло (MC, QMC) с техниками снижения размерности (SD, PCA, CHOL, BBD) показывает, что для европейского колл-опциона с параметрами [latex]D=80[/latex], [latex]\rho=0.6[/latex] и [latex]\epsilon=10^{-3}[/latex], QMC-методы обеспечивают сходимость к 1% и 0.1% точности, при этом комбинации с различными техниками снижения размерности демонстрируют схожую производительность. — Сравнение различных методов Монте-Карло (MC, QMC) с техниками снижения размерности (SD, PCA, CHOL, BBD) показывает, что для европейского колл-опциона с параметрами $D=80$ , $\rho=0.6$ и $\epsilon=10^{-3}$ , QMC-методы обеспечивают сходимость к 1% и 0.1% точности, при этом комбинации с различными техниками снижения размерности демонстрируют схожую производительность.

Практическое Применение: Комплексные Финансовые Инструменты

Метод Монте-Карло, в сочетании с техниками снижения дисперсии, является ключевым инструментом для оценки стоимости и управления рисками при работе со сложными финансовыми инструментами, такими как азиатские опционы и европейские корзинные опционы. Данные инструменты характеризуются зависимостью выплат от нескольких базовых активов и временных периодов, что делает аналитическое ценообразование затруднительным. Использование методов снижения дисперсии, таких как стратифицированная выборка или важностная выборка, позволяет существенно уменьшить количество необходимых симуляций для достижения заданной точности оценки, что критически важно для практического применения в условиях ограниченных вычислительных ресурсов и требований к скорости расчетов.

Оценка стоимости и рисков сложных финансовых инструментов, таких как азиатские и корзинные опционы, требует вычисления выплат, зависящих от нескольких базовых активов и временных периодов. Выплаты по этим инструментам не определяются простой формулой, а являются результатом сложных вычислений, учитывающих изменение цен на несколько активов на протяжении определенного времени. Например, выплата по азиатскому опциону зависит от средней цены базового актива за период, а выплата по корзинному опциону — от наихудшей или наилучшей доходности из группы активов. Сложность вычислений обусловлена необходимостью моделирования динамики нескольких активов и учета корреляций между ними, что делает аналитические решения невозможными и требует использования численных методов, таких как метод Монте-Карло.

Для оптимизации процесса моделирования сложных финансовых инструментов применяются передовые методы, такие как броуновские мосты и анализ главных компонент. Броуновские мосты позволяют улучшить дискретизацию траекторий, обеспечивая более точное приближение к реальным рыночным сценариям, особенно при моделировании путей, зависящих от времени. Анализ главных компонент (PCA) эффективно снижает размерность задачи, выявляя основные факторы, определяющие поведение нескольких базовых активов. Это достигается путем преобразования коррелированных активов в некоррелированные главные компоненты, что значительно уменьшает вычислительную сложность и повышает скорость моделирования, особенно при работе с портфелями, содержащими большое количество активов. Использование PCA позволяет сократить число случайных переменных, необходимых для моделирования, без существенной потери точности.

Алгоритмическая дифференциация, использующая адъюнкт-метод (AAD), представляет собой эффективный способ вычисления чувствительностей финансовых инструментов. В отличие от метода конечных разностей, AAD позволяет снизить вычислительные затраты в 4 раза. Важно отметить, что относительные затраты при использовании AAD остаются постоянными вне зависимости от количества базовых активов, что делает его особенно выгодным при работе со сложными портфелями и инструментами, зависящими от множества факторов. Этот подход позволяет значительно ускорить процесс оценки рисков и оптимизации стратегий.

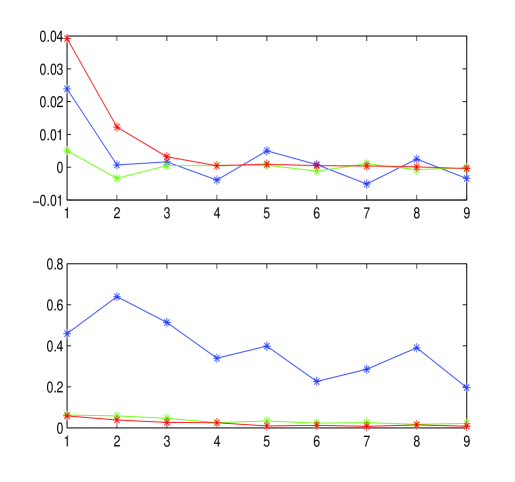
Сравнительный анализ различных стратегий сэмплирования (стандартная дискретизация, факторизация Холецкого, броуновский мост, PCA) при ценообразовании азиатского колл-опциона в восьмимерном пространстве показывает влияние выбранного метода на показатели чувствительности [latex]S_i[/latex] и [latex]S_i^{tot}[/latex] к различным факторам риска. — Сравнительный анализ различных стратегий сэмплирования (стандартная дискретизация, факторизация Холецкого, броуновский мост, PCA) при ценообразовании азиатского колл-опциона в восьмимерном пространстве показывает влияние выбранного метода на показатели чувствительности $S_i$ и $S_i^{tot}$ к различным факторам риска.

Взгляд в Будущее: Преодоление Современных Ограничений

Постоянные исследования в области адаптивных методов выборки и эффективного снижения дисперсии открывают новые горизонты для повышения производительности методов Монте-Карло. Эти методы позволяют целенаправленно концентрировать вычислительные ресурсы на наиболее значимых областях пространства параметров, избегая избыточного анализа менее важных областей. Благодаря этому, удается существенно сократить время расчетов и повысить точность получаемых результатов, особенно в задачах, характеризующихся высокой сложностью и многомерностью. Разработка более совершенных алгоритмов адаптивной выборки, учитывающих специфику конкретной задачи, и применение инновационных техник снижения дисперсии, таких как стратифицированная выборка или методы контрольных переменных, позволяют получать более надежные и точные оценки в условиях ограниченных вычислительных ресурсов. Дальнейшее развитие этих направлений позволит решать задачи, ранее считавшиеся недоступными для анализа с использованием методов Монте-Карло.

Исследования показывают, что комбинирование различных методов моделирования открывает новые горизонты в изучении сложных финансовых явлений. Традиционно, финансовые модели часто опираются на один конкретный подход, будь то метод Монте-Карло, конечно-разностные схемы или деревья решений. Однако, интеграция этих методов позволяет использовать сильные стороны каждого из них, компенсируя их недостатки. Например, сочетание метода Монте-Карло, обеспечивающего гибкость в моделировании сложных сценариев, с более быстрыми, но менее гибкими, численными методами, позволяет добиться высокой точности при разумных вычислительных затратах. Такой гибридный подход особенно полезен при моделировании производных финансовых инструментов, оценке рисков в условиях неопределенности и прогнозировании поведения финансовых рынков. Разработка и применение подобных гибридных стратегий представляется перспективным направлением для повышения надежности и эффективности финансовых моделей в будущем.

Разработка надежных и масштабируемых вычислительных платформ становится критически важной задачей в связи с постоянным усложнением финансовых моделей и увеличением объемов обрабатываемых данных. Современные финансовые инструменты, такие как моделирование деривативов и оценка рисков, требуют все больше вычислительных ресурсов. Эффективная реализация этих моделей на практике невозможна без оптимизированных алгоритмов и инфраструктуры, способной обрабатывать большие объемы информации в реальном времени. Инвестиции в создание таких платформ, использующих, например, параллельные вычисления и облачные технологии, позволят значительно повысить точность и скорость финансовых расчетов, а также открыть новые возможности для анализа и прогнозирования рыночных тенденций. Подобные решения не только улучшат управление рисками, но и позволят более эффективно использовать финансовые ресурсы.

Современные финансовые рынки характеризуются постоянно растущей сложностью и взаимосвязанностью, что требует от методов управления рисками большей адаптивности и точности. Развитие вычислительных технологий и, в частности, усовершенствование методов моделирования, таких как Монте-Карло, становится не просто желательным, а необходимым условием для эффективной навигации в этой среде. Повышение производительности и масштабируемости этих методов позволит анализировать более сложные сценарии, учитывать больше факторов неопределенности и, как следствие, принимать более обоснованные решения в условиях постоянно меняющихся рыночных условий. В конечном итоге, эти усовершенствования способствуют укреплению финансовой стабильности и снижению системных рисков, обеспечивая более надежную защиту от потенциальных потрясений.

Сравнение методов Монте-Карло (MC+SD), квази-Монте-Карло с коррекцией ББД (rQMC+BBD) и чистого квази-Монте-Карло с коррекцией ББД (QMC+BBD) для опциона «азиатский колл» при $D=32$ и $\epsilon=10^{-3}$ показывает, что лог-доходности и волатильность сближаются при увеличении числа траекторий симуляции от 100 до 10,000.

Исследование, представленное в данной работе, демонстрирует, как оптимизация методов Монте-Карло и квази-Монте-Карло, в сочетании с глобальным анализом чувствительности, способна значительно повысить эффективность ценообразования финансовых деривативов. Этот подход позволяет не просто снизить вычислительные затраты, но и получить более точную оценку рисков, что критически важно для стабильности финансовых рынков. Как отмечал Юрген Хабермас: «Коммуникативное действие — это действие, ориентированное на достижение взаимопонимания». В контексте данной работы, это означает, что ясное и эффективное моделирование финансовых инструментов требует не только математической точности, но и способности «коммуницировать» сложность рыночных процессов в понятной форме, позволяющей принимать обоснованные решения. Особое внимание к снижению дисперсии и оптимизации выборки, представленное в исследовании, подчеркивает важность структурированного подхода к решению сложных задач.

Куда двигаться дальше?

Представленная работа, демонстрируя эффективность методов квази-Монте-Карло и глобального анализа чувствительности, лишь аккуратно приподнимает край покрывала над истинной сложностью оценки производных финансовых инструментов. Все методы, даже самые элегантные, неизбежно сталкиваются с проклятием размерности. Искоренение шума не означает устранение структурной хрупкости; уменьшение дисперсии не гарантирует устойчивости системы. Всё ломается по границам ответственности — если их не видно, скоро будет больно. Повышение точности оценки «греков» — это лишь следствие, а не причина, стабильности финансовой системы.

Следующим шагом видится не столько дальнейшая оптимизация существующих алгоритмов, сколько разработка принципиально новых подходов к моделированию. Необходим переход от «чёрных ящиков» к прозрачным, интерпретируемым моделям, позволяющим не только оценить риск, но и понять его природу. Следует обратить внимание на методы, позволяющие эффективно оценивать взаимосвязи между параметрами и чувствительность результатов к изменениям в этих параметрах, особенно в условиях нелинейности и неопределенности. Умение выявлять критические точки и слабые места в системе — вот истинный навык, определяющий долгосрочную устойчивость.

Эффективное измерение “эффективной размерности” системы, указанное в работе, — это лишь первый шаг. Понимание того, как эта размерность меняется во времени и как она влияет на стабильность модели, — вот задача, требующая дальнейших исследований. В конечном итоге, финансовые модели — это лишь приближения к реальности. Задача исследователя — не создать идеальную модель, а разработать инструменты, позволяющие адекватно оценивать погрешности и ограничения этих моделей.

Оригинал статьи: https://arxiv.org/pdf/2602.14354.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-17 16:19