Моделирование нелинейных систем: новый подход на основе оператора Купмана

Автор: Денис Аветисян

В статье представлен инновационный метод идентификации нелинейных систем, использующий билинейную реализацию оператора Купмана и оптимизацию радиальных базисных функций.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Долгосрочная прогностическая способность моделей [latex] y_1 [/latex] и [latex] y_2 [/latex] демонстрирует их эффективность в предсказании поведения системы на тестовых данных, полученных в ходе моделирования. — Долгосрочная прогностическая способность моделей $y_1$ и $y_2$ демонстрирует их эффективность в предсказании поведения системы на тестовых данных, полученных в ходе моделирования.

Разработанный подход позволяет повысить точность многошагового прогнозирования и управления сложными системами, такими как воздушные тракты дизельных двигателей.

Нелинейные системы представляют собой серьезную проблему для точного долгосрочного прогнозирования, особенно при ограниченных измерениях состояния. В данной работе, посвященной ‘Generalized bilinear Koopman realization from input-output data for multi-step prediction with metaheuristic optimization of lifting function and its application to real-world industrial system’, предложен новый подход к моделированию на основе оператора Купмана, использующий билинейную реализацию и оптимизацию радиальных базисных функций. Показано, что предложенная методология значительно превосходит традиционные линейные модели Купмана в задачах прогнозирования, особенно применительно к сложным промышленным системам, таким как система управления воздушным потоком дизельного двигателя. Возможно ли дальнейшее повышение точности и робастности модели за счет адаптации структуры билинейной реализации к специфике конкретной системы?

Преодолевая Сложность: Вызовы в Моделировании Нелинейных Систем

Традиционные методы идентификации систем, такие как ARX и N4SID, часто оказываются неэффективными при работе с высоко нелинейной динамикой, характерной для многих реальных систем. Эти подходы, разработанные для линейных моделей, испытывают трудности при адекватном описании сложных взаимосвязей и явлений, возникающих в нелинейных системах. Неспособность точно отразить нелинейное поведение приводит к значительным погрешностям в прогнозировании и управлении, ограничивая их применимость в таких областях, как робототехника, биомедицинская инженерия и экономическое моделирование. В результате возникает потребность в разработке и применении более сложных методов, способных эффективно обрабатывать нелинейности и обеспечивать высокую точность моделирования.

Линейные подходы к моделированию сложных систем, несмотря на свою математическую элегантность, зачастую требуют существенного упрощения описываемых физических процессов. Это неизбежно приводит к неточностям в прогнозировании поведения системы и снижает эффективность управления ею. Упрощения, необходимые для применения стандартных алгоритмов идентификации, могут игнорировать важные нелинейные эффекты, взаимодействия между компонентами и другие факторы, существенно влияющие на реальное поведение системы. В результате, модель, хотя и математически удобная, не способна адекватно отразить всю сложность исходного объекта, ограничивая возможности точного предсказания и оптимизации его характеристик. Неспособность учесть эти нюансы особенно критична в задачах, где требуется высокая точность, например, в управлении сложными технологическими процессами или прогнозировании динамики финансовых рынков.

Точность моделирования играет ключевую роль в управлении сложными системами, их оптимизации и прогнозировании будущего поведения. Недостаточно точные модели приводят к неэффективным алгоритмам управления, неоптимальным решениям и ошибочным прогнозам, что может иметь серьезные последствия в различных областях, от энергетики и финансов до робототехники и биологии. В связи с этим, возникает потребность в разработке и применении более совершенных инструментов моделирования, способных адекватно описывать нелинейные зависимости, хаотическое поведение и другие особенности сложных систем. Такие инструменты позволяют не только лучше понимать принципы функционирования этих систем, но и эффективно управлять ими, оптимизировать их работу и предсказывать их реакцию на различные воздействия, открывая новые возможности для инноваций и прогресса.

Экспериментальное тестирование показало, что модели [latex]y_1[/latex] и [latex]y_2[/latex] демонстрируют стабильную долгосрочную предсказательную способность. — Экспериментальное тестирование показало, что модели $y_1$ и $y_2$ демонстрируют стабильную долгосрочную предсказательную способность.

Оператор Купмана: Элегантное Решение для Нелинейных Систем

Оператор Купмана предоставляет возможность отобразить нелинейную динамику в бесконечномерное пространство, где она становится линейной. Это преобразование позволяет применять стандартные методы линейной идентификации систем, такие как анализ в частотной области и прогнозирование с помощью линейных моделей. Суть подхода заключается в построении наблюдаемой функции $\mathcal{K}$ , которая действует на нелинейную систему и переводит её в эквивалентную линейную систему в пространстве наблюдаемых. Таким образом, несмотря на сложность исходной нелинейной динамики, анализ и управление системой могут быть выполнены с использованием инструментов, предназначенных для линейных систем, что значительно упрощает процесс моделирования и контроля.

Линейные модели оператора Купмана (LTI Koopman Models) расширяют базовый подход, предоставляя линейное представление нелинейных систем в бесконечномерном пространстве. Несмотря на это, их эффективность ограничена при работе с системами, демонстрирующими выраженные нелинейности. Это связано с тем, что линейное приближение может недостаточно точно отражать поведение системы в областях фазового пространства, где нелинейные эффекты доминируют. В результате, точность предсказаний и управления системой, смоделированной с помощью LTI Koopman Models, может снижаться при наличии сильных нелинейностей, требуя использования более сложных моделей для обеспечения адекватного представления динамики.

Переход к билинейным моделям оператора Купмана позволяет повысить точность моделирования за счет захвата билинейной динамики. В отличие от линейных моделей оператора Купмана (LTI), которые могут испытывать ограничения при описании сильно нелинейных систем, билинейные модели эффективно описывают взаимодействия между состояниями системы, включающие произведения координат состояния. Это достигается путем использования билинейных базисных функций при построении оператора Купмана, что позволяет более адекватно представлять сложные нелинейные зависимости и, как следствие, улучшает точность прогнозирования и управления нелинейными системами. Такой подход особенно важен при моделировании систем, где нелинейности существенно влияют на их поведение, например, в задачах аэродинамики, робототехники и химических реакций.

Внедрение и Оптимизация для Достижения Высокой Точности

Билинейные модели Купмана требуют оптимизации для определения функций лифтинга, наилучшим образом представляющих нелинейную динамику системы. Процесс оптимизации заключается в поиске таких функций, которые минимизируют расхождение между предсказаниями модели и фактическим поведением системы. В качестве эффективного инструмента для решения этой задачи часто используется оптимизация роем частиц (PSO). PSO представляет собой метод глобальной оптимизации, основанный на популяции частиц, которые перемещаются в пространстве поиска, руководствуясь собственной лучшей позицией и лучшей позицией роя. Применение PSO позволяет эффективно находить оптимальные параметры функций лифтинга, обеспечивая высокую точность моделирования нелинейных систем.

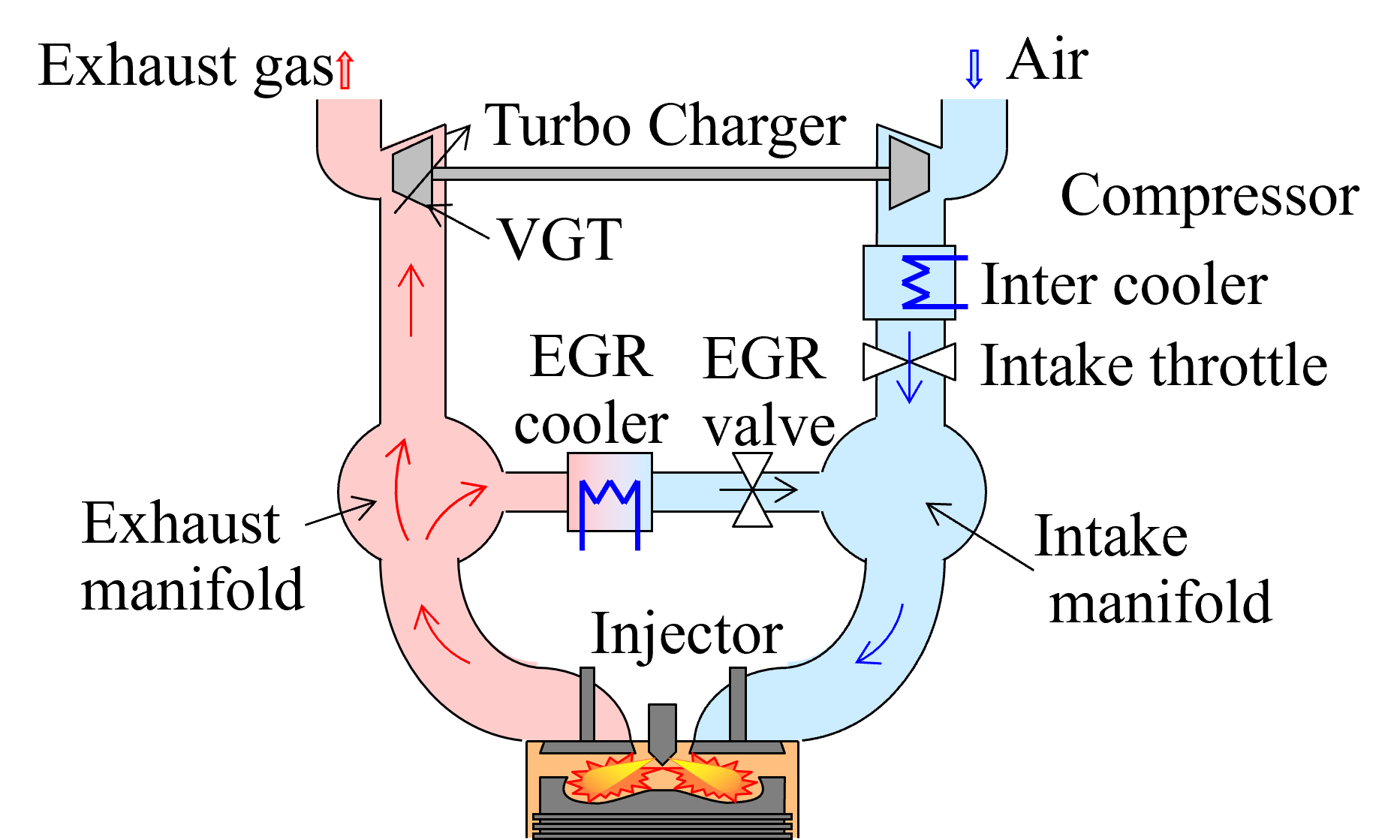
Применение методов билинейных моделей Купмана к системе воздушного тракта дизельного двигателя продемонстрировало возможность эффективного моделирования сложного процесса сгорания. Это позволяет получить точное представление о нелинейной динамике системы, что, в свою очередь, открывает перспективы для улучшения алгоритмов управления двигателем и оптимизации его работы. В частности, моделирование позволило учесть взаимосвязи между параметрами, влияющими на процесс сгорания, и повысить точность прогнозирования характеристик двигателя в различных режимах работы. Полученные результаты указывают на потенциал использования данных методов для разработки более эффективных и экологичных дизельных двигателей.

Идентификация моделей осуществляется на основе данных «вход-выход» в сочетании с использованием координат временной задержки, что обеспечивает устойчивость процесса. Оценка точности модели производится с использованием метрики R-squared, которая на симулированных и экспериментальных данных превышает значение 0.90. Такой подход позволяет эффективно выявлять динамику системы и обеспечивает высокую степень соответствия модели реальным данным, что подтверждается достигнутыми значениями коэффициента детерминации $R^2$ .

Схема представляет собой систему воздухозабора дизельного двигателя.

Расширение Горизонтов: Продвинутые Методы и Перспективы Развития

В дополнение к базовым моделям Купмана, такие методы, как EDMD (Extended Dynamic Mode Decomposition) и SINDy (Sparse Identification of Nonlinear Dynamics), значительно расширяют возможности выявления и анализа нелинейной динамики сложных систем. EDMD позволяет более эффективно извлекать динамические моды из данных, даже в случаях, когда традиционные методы оказываются неэффективными. SINDy, в свою очередь, использует разреженные регрессии для идентификации основных нелинейных членов в уравнениях динамики, что позволяет строить компактные и интерпретируемые модели. Сочетание этих подходов с классическим фреймворком Купмана открывает новые перспективы для понимания и прогнозирования поведения сложных систем в различных областях науки и техники, от гидродинамики и метеорологии до биохимии и экономики.

Применение рекуррентных нейронных сетей, включая сети LSTM и модели NARX, в сочетании с фреймворком Купмана, открывает новые возможности для прогнозирования и управления сложными системами. В то время как традиционные модели Купмана опираются на линейные аппроксимации, нейронные сети способны улавливать нелинейные зависимости в данных, значительно повышая точность предсказаний. Сети LSTM, благодаря своей способности сохранять информацию о прошлых состояниях, особенно эффективны при работе с временными рядами и динамическими системами. Модели NARX, использующие прошлые и текущие значения входных данных, позволяют более точно моделировать зависимости в данных и улучшать управляемость систем. Сочетание этих нейросетевых подходов с аналитическими преимуществами фреймворка Купмана позволяет создавать гибридные модели, способные решать задачи, недоступные для каждого из подходов по отдельности, что является перспективным направлением в области машинного обучения и управления сложными системами.

Развитые методы анализа динамических систем, такие как расширенные модели Купмана, EDMD и SINDy, демонстрируют впечатляющую универсальность, находя применение в самых разных областях. От моделирования турбулентных потоков в гидродинамике и прогнозирования поведения сложных финансовых рынков, до анализа климатических изменений и разработки систем управления роботами — эти инструменты позволяют исследовать нелинейные процессы, ранее считавшиеся непостижимыми. Возможность выявления скрытых закономерностей и долгосрочных трендов открывает перспективы для значительных прорывов в науке и технике, позволяя создавать более точные прогнозы, оптимизировать существующие системы и разрабатывать принципиально новые технологии. Подобный междисциплинарный подход обещает не только углубление понимания сложных явлений, но и создание инновационных решений для широкого спектра практических задач.

Представленное исследование демонстрирует элегантный подход к моделированию нелинейных систем, используя билинейную реализацию оператора Купмана. Авторы, стремясь к последовательности в представлении данных, оптимизируют радиальные базисные функции, что позволяет достичь высокой точности прогнозирования в многошаговых задачах. Этот метод, применимый к сложным промышленным системам, таким как дизельные двигатели, подчеркивает важность гармонии между формой и функцией в инженерных решениях. Как заметил Томас Гоббс: «Люди больше боятся наказания, чем смерти». В контексте управления сложными системами, точность моделирования, достигнутая в данной работе, служит своего рода «наказанием» для погрешностей и неопределенностей, обеспечивая надежность и эффективность.

Куда Далее?

Представленная работа, несомненно, расширяет инструментарий для идентификации нелинейных систем. Однако, стоит признать, что элегантность решения не всегда гарантирует его универсальность. Оптимизация радиальных базисных функций, хотя и демонстрирует улучшенные результаты в контексте дизельных двигателей, оставляет открытым вопрос о её масштабируемости к системам с существенно большей размерностью и сложностью. Поиск оптимального баланса между точностью модели и вычислительной сложностью остаётся краеугольным камнем, требующим дальнейшего осмысления.

Особый интерес представляет возможность интеграции данного подхода с другими методами машинного обучения, такими как обучение с подкреплением. Создание гибридных систем, способных к адаптации в реальном времени и самообучению, представляется не просто желательным, но и необходимым шагом для решения задач управления в динамически меняющихся условиях. Простое наращивание сложности модели, без глубокого понимания лежащих в её основе принципов, подобно украшению сломанного механизма — привлекательно, но бессмысленно.

В конечном итоге, истинная ценность подобного рода исследований заключается не в достижении абсолютной точности, а в создании инструментов, позволяющих лучше понимать природу нелинейности и эффективно управлять ею. Поиск минимально достаточного, но при этом надежного и интерпретируемого представления системы — вот та задача, которая требует дальнейших усилий и философского осмысления.

Оригинал статьи: https://arxiv.org/pdf/2602.15422.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-19 00:15