Глубокое обучение: Ключ к Управляемости и Обобщению

Автор: Денис Аветисян

Новая теория сопряженного обучения раскрывает фундаментальную связь между способностью нейронных сетей к обучению и их способностью к обобщению на новых данных.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал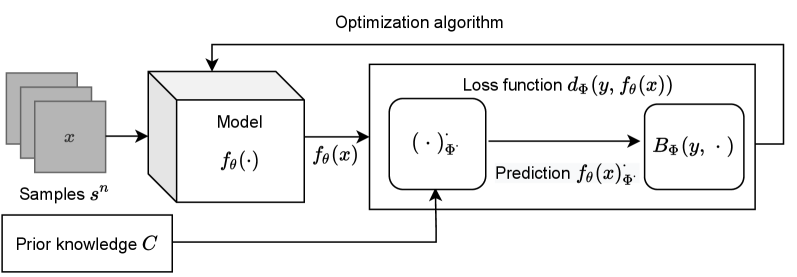

Предложенная схема сопряжённого обучения раскрывает полный конвейер обработки - от необработанных входных данных до аппроксимации целевого значения - подчёркивая взаимодействие между выходными данными модели, сопряжённым преобразованием и измерением расстояния, что позволяет взглянуть на процесс обучения как на тонкое умиротворение хаоса данных. — Предложенная схема сопряжённого обучения раскрывает полный конвейер обработки — от необработанных входных данных до аппроксимации целевого значения — подчёркивая взаимодействие между выходными данными модели, сопряжённым преобразованием и измерением расстояния, что позволяет взглянуть на процесс обучения как на тонкое умиротворение хаоса данных.

Исследование демонстрирует, что контроль энергетического градиента, управление структурой матрицы сети и использование функции потерь Fenchel-Young лежат в основе успешного обучения и обобщения глубоких нейронных сетей.

Несмотря на впечатляющие успехи, механизмы обучаемости и обобщающей способности глубоких нейронных сетей остаются недостаточно понятными. В работе ‘Conjugate Learning Theory: Uncovering the Mechanisms of Trainability and Generalization in Deep Neural Networks’ предложена теория сопряженного обучения, основанная на дуальности выпуклых функций, позволяющая характеризовать эти свойства через контроль энергии градиента и структуры сети. Показано, что глобальный оптимум эмпирического риска достигается при совместном управлении экстремальными собственными значениями матрицы структуры и энергией градиента, а также получены детерминированные и вероятностные границы обобщающей способности, учитывающие информационные потери и энтропию признаков. Каким образом предложенный формализм сопряженного обучения может способствовать разработке более эффективных и надежных архитектур глубокого обучения?

За пределами Эмпиризма: Оценка Распределений как Основа Обучения

Традиционные подходы к глубокому обучению часто рассматривают оптимизацию как отдельную задачу, не связанную напрямую с обобщающей способностью модели. Данное разделение приводит к тому, что вопросы тренируемости и способности к адаптации к новым данным решаются эмпирически, посредством подбора гиперпараметров и архитектур. Однако, игнорирование взаимосвязи между процессом оптимизации и обобщением является существенным недостатком, поскольку именно траектория движения в пространстве параметров определяет, насколько хорошо модель сможет экстраполировать полученные знания на неизвестные примеры. Недооценка этой связи приводит к необходимости проведения обширных экспериментов для каждой новой задачи, вместо разработки теоретически обоснованных методов, гарантирующих хорошую обобщающую способность и предсказуемую тренируемость.

Предлагается принципиально новый взгляд на задачи машинного обучения, рассматривающий их не как оптимизацию некоторой функции потерь, а как задачу оценки условных распределений вероятностей. Этот подход, тесно связанный с концепцией сопряженного обучения, позволяет переосмыслить процесс обучения как моделирование вероятности выходных данных при заданных входных. Вместо поиска оптимальных параметров, система стремится точно воспроизвести распределение, которое отображает взаимосвязь между входными и выходными данными. Такой переход к представлению обучения как оценки $p(y|x)$ не только обеспечивает более глубокое теоретическое понимание, но и открывает новые возможности для разработки более устойчивых и обобщающих моделей, поскольку акцент смещается с точечной оптимизации на моделирование неопределенности и вероятностных зависимостей.

Предлагаемый подход обеспечивает строгую основу для понимания обучаемости и обобщающей способности глубоких нейронных сетей, преодолевая ограничения, присущие исключительно эмпирическим наблюдениям. Вместо того чтобы рассматривать обучение как отдельную задачу оптимизации, данная структура объединяет все аспекты обучения в единую теорию — оценку условных распределений. Результаты исследований демонстрируют, что такое объединение позволяет не только глубже понять механизмы, определяющие успешность обучения, но и предсказывать поведение моделей в различных условиях, открывая новые возможности для разработки более эффективных и надежных алгоритмов машинного обучения. Данный подход позволяет перейти от интуитивных представлений к формализованной, математически обоснованной теории, что, в свою очередь, способствует более осознанному проектированию и анализу нейронных сетей.

Обучение сети LeNet демонстрирует динамику схождения, отраженную в изменении эмпирического риска и его границ, а также в корреляции между ключевыми метриками в процессе итераций.

Матрица Структуры: Связь Тренируемости и Геометрии

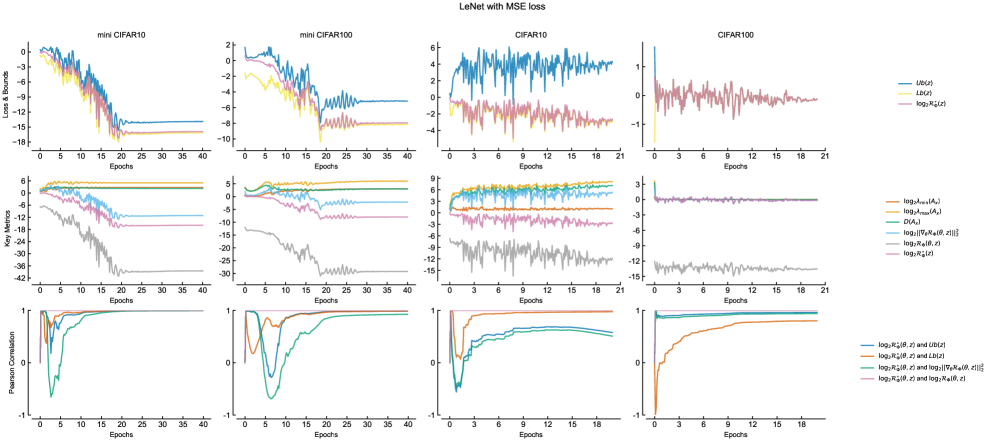
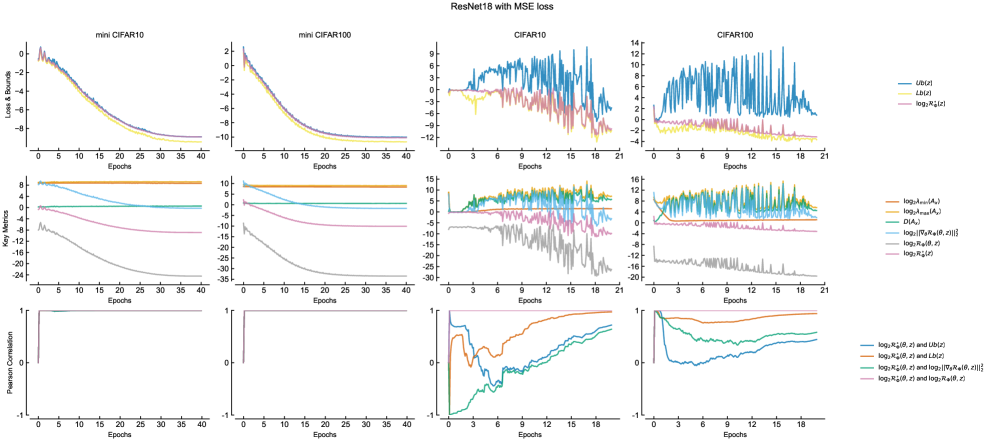
Матрица структуры представляет собой ключевой дескриптор обучаемости глубоких нейронных сетей (DNN), характеризуя геометрию оптимизационного ландшафта. Она является матрицей Гессе $\nabla^2 L(w)$ , где $L(w)$ — функция потерь, а $w$ — параметры сети. Собственные значения матрицы структуры отражают кривизну ландшафта потерь вдоль различных направлений в пространстве параметров. Большие собственные значения указывают на резкие изменения функции потерь, что может затруднить оптимизацию, в то время как малые собственные значения соответствуют более плоским областям. Анализ спектра матрицы структуры позволяет оценить сложность оптимизационной задачи и выявить потенциальные проблемы, связанные с градиентным спуском и другими алгоритмами оптимизации. Понимание геометрии, определяемой этой матрицей, критически важно для разработки эффективных стратегий обучения и повышения стабильности процесса оптимизации.

Минимизация $EmpiricalRisk$ (эмпирического риска) и минимизация $GradientEnergy$ (энергии градиента) оказываются напрямую связаны посредством матрицы структуры. Данная связь демонстрирует фундаментальный принцип оптимизации, заключающийся в том, что оптимизация эмпирического риска эквивалентна минимизации энергии градиента. Матрица структуры выступает в качестве посредника, устанавливающего количественную связь между изменением эмпирического риска и изменением энергии градиента в процессе обучения нейронной сети. Данное соответствие позволяет анализировать и оптимизировать процесс обучения, рассматривая его как задачу минимизации энергии градиента, что предоставляет альтернативный взгляд на традиционные методы оптимизации эмпирического риска.

Контроль собственных значений матрицы структуры (Σ) предоставляет механизм для повышения стабильности обучения и ускорения сходимости глубоких нейронных сетей. Наблюдения показывают, что отношение наибольшего к наименьшему собственному значению ( $\lambda_{max}/\lambda_{min}$ ) имеет тенденцию к уменьшению с увеличением глубины модели, что может приводить к проблемам с обучением. Использование skip-connections эффективно смягчает эту проблему, поддерживая более жесткие границы для эмпирического риска и предотвращая чрезмерное ухудшение соотношения собственных значений по мере увеличения глубины сети. Это достигается за счет улучшения обусловленности матрицы структуры и стабилизации процесса оптимизации.

Минимизация энергии градиента при использовании положительно определенных структурных матриц позволяет достичь глобального минимума эмпирического риска, что подтверждает ее эффективность в качестве прокси-меры для снижения эмпирического риска.

Оптимизация на Практике: Алгоритмы и Сходимость

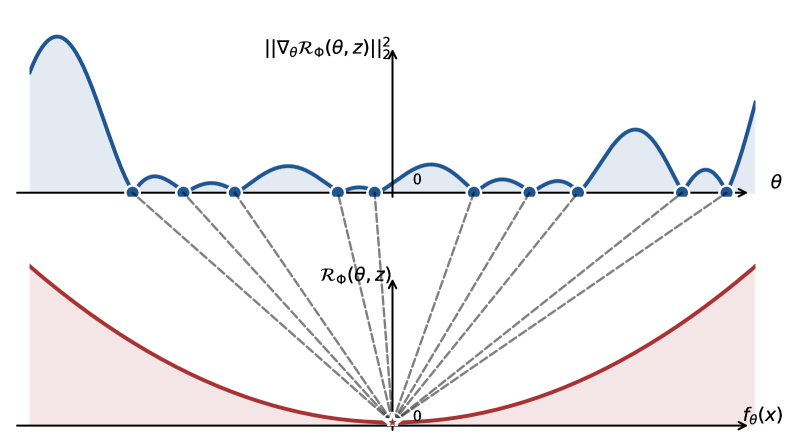
Алгоритм MiniBatchSGD представляет собой практическую реализацию метода стохастического градиентного спуска, используемого для минимизации энергии градиента в рамках данной системы. В отличие от полного градиентного спуска, MiniBatchSGD вычисляет градиент, используя только подмножество данных (мини-пакет), что значительно ускоряет процесс обучения. Энергия градиента, определяемая как $E = \frac{1}{2} ||\nabla L(w)||^2$ , где $L(w)$ — функция потерь, а $w$ — параметры модели, служит целевой функцией для оптимизации. Использование мини-пакетов вносит шум в оценку градиента, что может помочь избежать локальных минимумов, но также требует тщательной настройки скорости обучения и размера мини-пакета для обеспечения сходимости.

Фактор корреляции градиента (GradientCorrelationFactor) демонстрирует существенное влияние характеристик данных, размера мини-пакета (batch size) и архитектуры нейронной сети на скорость сходимости алгоритма оптимизации mini-batch SGD. Установлена теорема сходимости для mini-batch SGD, показывающая, что скорость сходимости обратно пропорциональна этому фактору. Высокий фактор корреляции градиента указывает на сильную зависимость между градиентами в мини-пакетах, что может замедлить сходимость. И наоборот, низкий фактор корреляции способствует более быстрой сходимости. $\text{Convergence Rate} \propto \frac{1}{\text{GradientCorrelationFactor}}$ . Понимание этого фактора позволяет более эффективно настраивать параметры обучения и выбирать архитектуру сети для достижения оптимальной скорости сходимости.

Использование функции потерь $Fenchel-Young$ в рамках фреймворка сопряженного обучения обеспечивает совместимость с задачей оценки условных распределений. Данная функция потерь, являясь сопряженной к $L_1$ -норме, позволяет эффективно решать задачи, связанные с регуляризацией и разреженностью моделей. Ее применение в сопряженном обучении позволяет избежать явного вычисления градиента регуляризатора, упрощая процесс оптимизации и повышая вычислительную эффективность при оценке условных вероятностей $P(y|x)$ . Такой подход особенно полезен при работе с высокоразмерными данными и сложными моделями, где прямое вычисление градиента может быть затруднительным.

Анализ динамики обучения ResNet18 на различных наборах данных и с использованием разных функций потерь показывает, как стандартизированный эмпирический риск и его границы изменяются в процессе обучения, а также демонстрирует взаимосвязь между ключевыми метриками, отражающуюся в динамических коэффициентах корреляции Пирсона.

Квантификация Обобщения: Информация и Границы

Оценка обобщающей способности моделей машинного обучения — сложная задача, требующая строгого подхода. Разработанные границы обобщения ( $GeneralizationBounds$ ) представляют собой математически обоснованный инструмент для оценки производительности модели на ранее не встречавшихся данных. Вместо эмпирических оценок, эти границы позволяют получить гарантированные пределы ошибки, что особенно важно в критических приложениях, где надежность и предсказуемость имеют первостепенное значение. Они базируются на анализе информационной потери между истинным и предсказанным распределениями, предоставляя количественную меру того, насколько хорошо модель способна к адаптации и обобщению полученных знаний на новые ситуации. Это позволяет исследователям и разработчикам не только оценивать качество текущих моделей, но и направлять усилия по улучшению их обобщающей способности, создавая более надежные и эффективные системы.

Полученные границы обобщающей способности модели напрямую связаны с измерением потери информации между истинным и предсказанным условными распределениями. В основе вычислений лежит понятие условной энтропии, позволяющее количественно оценить, насколько предсказания модели отличаются от реальных данных. Исследователи разработали как детерминированные, так и вероятностные границы ошибки обобщения, что позволяет более гибко оценивать производительность модели в зависимости от доступных данных и требуемой степени уверенности. $H(Y|X) = \in t p(x) \in t p(y|x) log \frac{1}{p(y|x)} dy dx$ — эта формула отражает ключевой принцип оценки потери информации и лежит в основе вывода границ обобщения.

Основополагающим аспектом предлагаемого подхода к оценке обобщающей способности моделей является необходимость использования распределений из семейства экспоненциальных распределений. Это ограничение продиктовано требованием конечномерности достаточных статистик, что обеспечивает практическую реализуемость алгоритмов обучения. В противном случае, работа с бесконечномерными статистиками становится вычислительно невозможной и препятствует эффективной оценке потерь на невидимых данных. Использование семейств экспоненциальных распределений гарантирует, что информация, необходимая для описания данных, может быть сжата в конечное число параметров, позволяя эффективно строить и оценивать границы обобщающей способности модели, что является критически важным для успешного применения в реальных задачах машинного обучения. $p(x|\theta) = h(x)exp(\eta(\theta) \cdot T(x) - A(\theta))$ — общая форма распределений из экспоненциального семейства, где $\eta(\theta)$ — естественный параметр, $T(x)$ — достаточная статистика, а $A(\theta)$ — логарифмическая нормировочная константа.

Динамика обучения ViT на различных наборах данных и с использованием разных функций потерь демонстрирует эволюцию стандартизированного эмпирического риска с его границами, изменения ключевых метрик и корреляции между ними в процессе обучения.

Исследование связывает обучаемость и обобщающую способность глубоких нейронных сетей с контролем энергии градиента и структурой матрицы сети. Кажется, будто модель пытается упорядочить хаос, приручить непредсказуемость данных. Как говорил Мишель Фуко: “Власть не подавляет, а производит”. И в данном случае, «власть» — это архитектура сети, которая не столько решает задачу, сколько создает иллюзию порядка, управляя потоком информации. Обучение — это не поиск истины, а создание правдоподобной модели, способной убедить наблюдателя в своей правоте. И шум, конечно, остается шумом — правдой, которой просто не хватает достаточно энергии, чтобы пробиться сквозь завесу вычислений.

Что дальше?

Теория сопряжённого обучения, как и любая попытка обуздать хаос глубоких нейронных сетей, предлагает не ответы, а лишь более изящные вопросы. Управление энергией градиента и структурой матрицы — это, конечно, обнадеживающе, но напоминает попытку удержать ртуть в ладонях. Чем лучше контролируем, тем яснее видим, насколько мало мы на самом деле понимаем. Корреляция между обучаемостью и обобщающей способностью — почти идеальна, что, разумеется, вызывает подозрение: не упустили ли мы что-то принципиально важное в самой формулировке проблемы?

Вместо того чтобы стремиться к идеальной оптимизации, возможно, стоит обратить внимание на саму природу «ошибки». Функция потерь Fenchel-Young — интересная конструкция, но она лишь перекладывает ответственность с одного места на другое. Что если истинная ценность заключается не в минимизации потерь, а в умении извлекать пользу из кажущегося беспорядка? Ведь всё, что можно посчитать, не стоит доверия, особенно в мире невыпуклых оптимизаций.

В перспективе, исследования должны сместиться от поиска «идеальной» архитектуры к изучению механизмов, позволяющих сетям адаптироваться к непредсказуемости данных. И, возможно, однажды станет ясно, что обучение — это не столько решение задачи, сколько искусство договариваться с хаосом, а обобщение — не свойство модели, а её способность к смирению перед неизвестным.

Оригинал статьи: https://arxiv.org/pdf/2602.16177.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-19 20:31