Автор: Денис Аветисян
Исследователи предлагают инновационный метод, использующий вероятностные распределения для повышения точности и эффективности калибровки социальных симуляторов в режиме реального времени.
"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.
Бесплатный Телеграм канал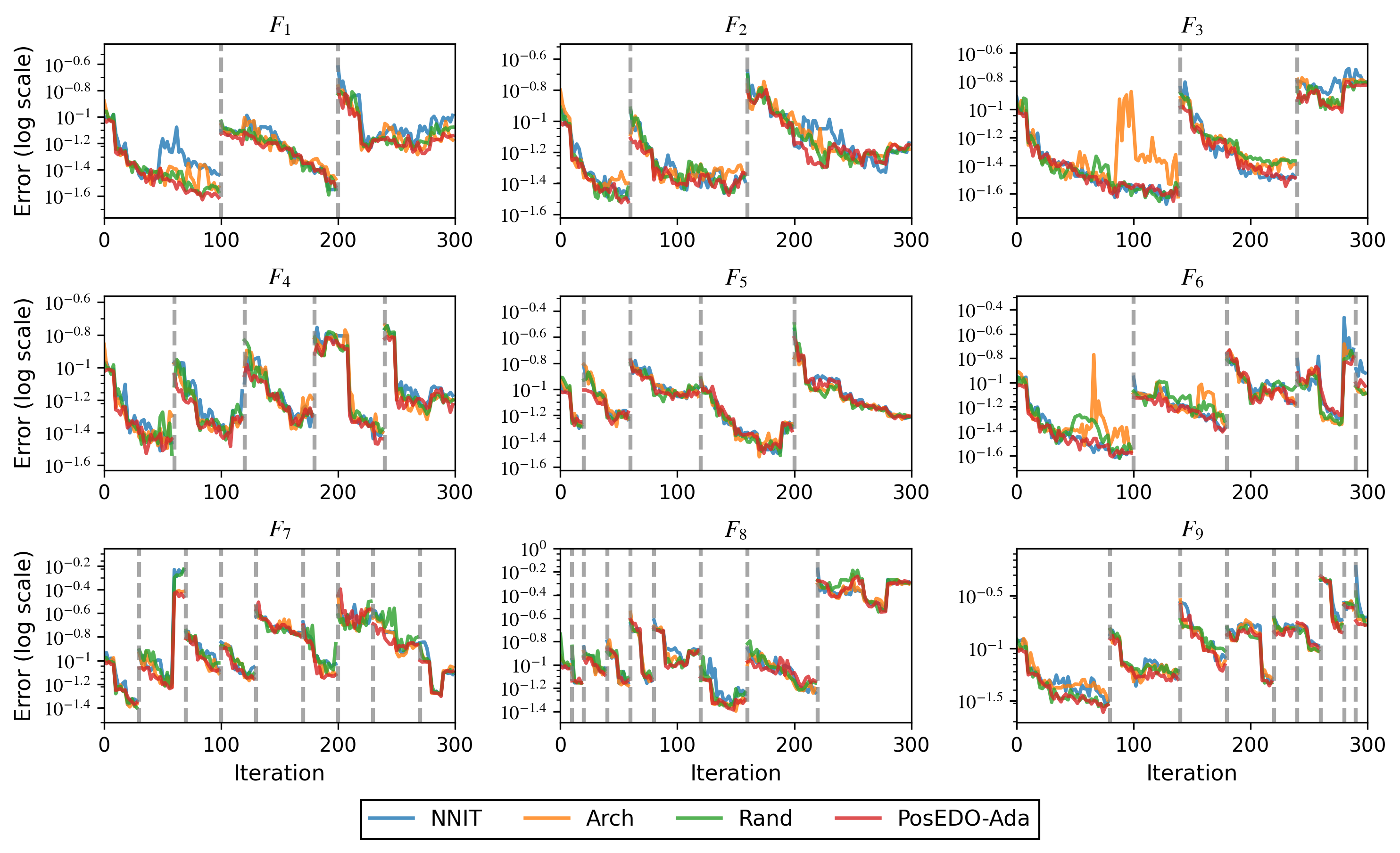
Предложенная методика PosEDO, основанная на эволюционной динамической оптимизации и потоковых моделях, демонстрирует превосходство над традиционными подходами к калибровке симуляторов.
Калибровка симуляторов сложных социальных систем представляет собой сложную задачу, особенно в условиях изменяющейся динамики реальных процессов. В работе, озаглавленной ‘Posterior Distribution-assisted Evolutionary Dynamic Optimization as an Online Calibrator for Complex Social Simulations’, предложен новый подход, использующий эволюционную динамическую оптимизацию (EDO) с опорой на апостериорные распределения параметров и наблюдаемых данных. Данный метод, PosEDO, позволяет адаптировать симуляторы к изменяющимся условиям, значительно превосходя традиционные EDO в задачах онлайн-калибровки. Не откроет ли это новые перспективы для моделирования и прогнозирования в социальных науках и смежных областях?
Неуловимая Динамика: Проблема Постоянно Меняющихся Систем
Многие реальные системы, будь то экономические модели или экологические сообщества, характеризуются изменчивостью и не являются статичными. Их внутренняя динамика постоянно эволюционирует под воздействием множества факторов, что делает невозможным точное описание и прогнозирование поведения на основе фиксированных, неизменных моделей. Например, в экономике потребительские предпочтения и рыночные условия могут кардинально меняться в течение короткого времени, а в экосистемах климатические изменения и появление новых видов оказывают существенное влияние на баланс популяций. Использование статических моделей в таких условиях приводит к постепенному отклонению от реальных данных и, как следствие, к неточным прогнозам и ошибочным управленческим решениям. Поэтому для адекватного понимания и моделирования сложных систем необходим учёт их динамической природы и постоянное обновление используемых моделей.
Традиционные методы калибровки параметров моделей часто оказываются неэффективными в динамически меняющихся системах. Когда основные характеристики системы со временем претерпевают изменения — будь то экономические циклы, колебания численности популяций или эволюция рыночных трендов — фиксированные параметры, установленные на основе начальных данных, быстро устаревают. Это приводит к явлению, известному как “дрейф модели”, когда прогнозы становятся все менее точными и надежными. По мере увеличения расхождения между моделью и реальным поведением системы, её предсказательная сила снижается, что может приводить к ошибочным решениям и неверным интерпретациям. Таким образом, для адекватного моделирования не статических, а изменяющихся систем, требуется постоянная адаптация параметров и переоценка базовых предположений.
Для адекватного описания и прогнозирования поведения сложных систем, таких как экономические модели или экологические сообщества, необходимо отказаться от статических подходов к моделированию. Вместо этого, эффективное моделирование требует непрерывного процесса адаптации, который учитывает изменяющуюся динамику системы. Этот процесс предполагает постоянный мониторинг данных, выявление отклонений от ожидаемых значений и последующую корректировку параметров модели. В результате, модель не просто пытается соответствовать текущему состоянию системы, но и способна предвидеть и адаптироваться к будущим изменениям, повышая точность прогнозов и обеспечивая более надежное понимание происходящих процессов. Использование адаптивных алгоритмов и методов машинного обучения позволяет модели «обучаться» на новых данных и автоматически корректировать свои параметры, что особенно важно в условиях нестационарности и высокой изменчивости окружающей среды.
Выявление Сдвига: Когда Модель Начинает «Лгать»
Обнаружение изменений является критически важным для поддержания точности моделей в динамичных средах, поскольку со временем происходят сдвиги в базовом поведении системы. Эти сдвиги, известные как дрифт данных или концептуальный дрифт, могут приводить к ухудшению производительности модели, если не будут своевременно обнаружены и устранены. В динамичных системах, где входные данные и взаимосвязи между ними постоянно меняются, регулярный мониторинг и выявление таких изменений необходимы для обеспечения надежности и актуальности модели. Отсутствие обнаружения изменений может привести к принятию неверных решений, основанных на устаревших данных и неверных предположениях.
Для количественной оценки изменений в данных и выявления отклонений от ожидаемого поведения используются методы, такие как расхождение Кульбака-Лейблера (KL Divergence) и статистическое обнаружение изменений. KL Divergence, измеряемая как D_{KL}(P||Q) = \sum_{i} P(i) \log \frac{P(i)}{Q(i)}, позволяет оценить разницу между двумя распределениями вероятностей, P и Q. Статистическое обнаружение изменений, в свою очередь, включает в себя мониторинг статистических свойств данных (например, среднего, дисперсии) и выявление значимых отклонений от установленных базовых значений или ожидаемых закономерностей. Значительные расхождения, определяемые на основе заданного порога, сигнализируют о необходимости адаптации модели или пересмотра ее параметров.
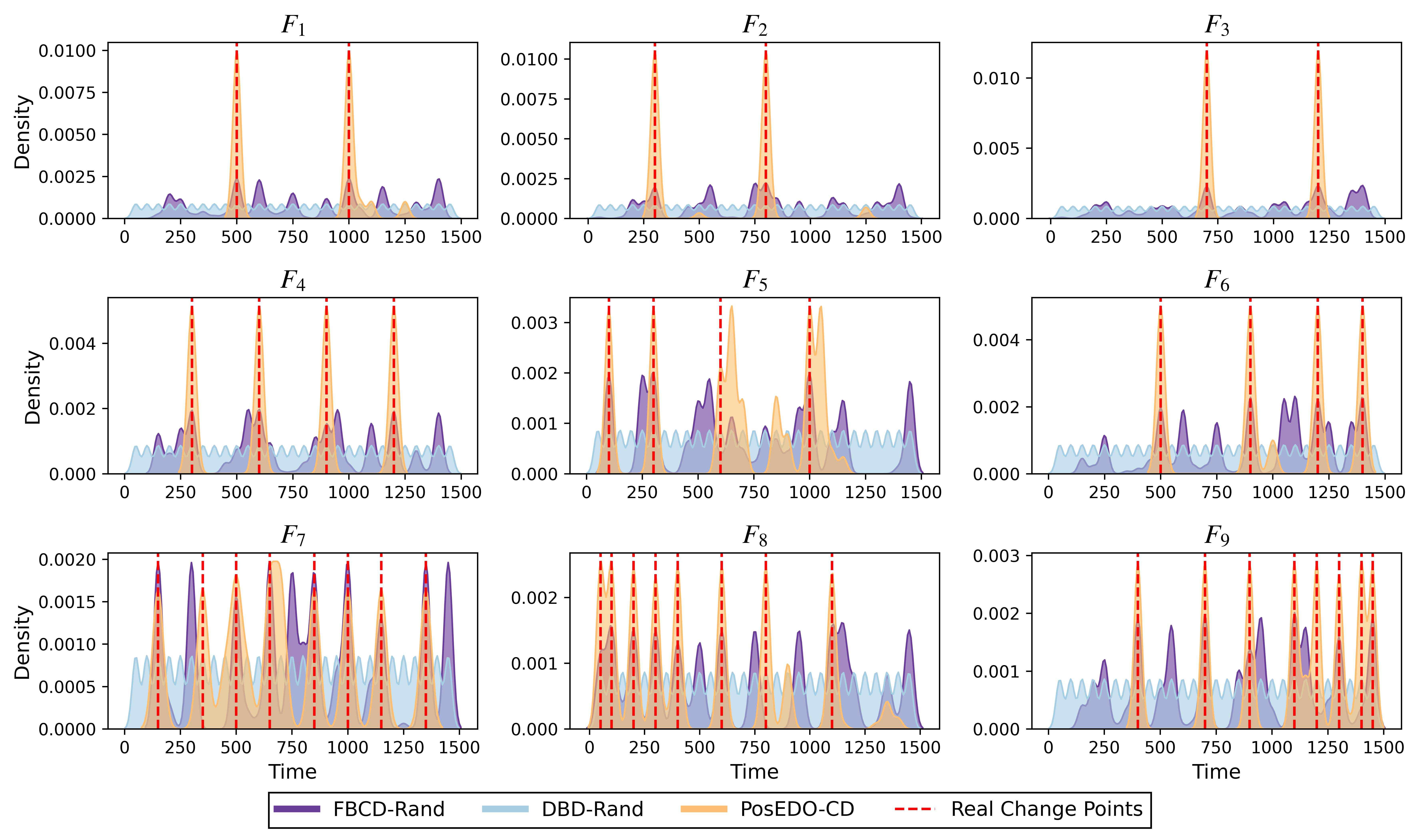
Практические реализации обнаружения необходимости изменений включают в себя методы Fitness-Based Change Detection (FBCD) и Detector-Based Detection (DBD), которые осуществляют мониторинг производительности модели для определения момента, когда требуется адаптация. В сравнительных исследованиях, PosEDO-CD демонстрирует более четкие и точные сигналы обнаружения изменений по сравнению с DBD-Rand и FBCD-Rand, что указывает на повышенную надежность и эффективность PosEDO-CD в контексте своевременного выявления отклонений в данных и необходимости переобучения модели.
Адаптация в Реальном Времени: Как Модель Учится «На Ходу»
Стратегии адаптации к изменяющейся среде позволяют моделям корректировать свои параметры в ответ на сдвиги в системе, поддерживая тем самым предсказательную способность. Данный подход критически важен в динамичных условиях, когда исходные предположения о данных перестают быть актуальными. Адаптация заключается в непрерывном обновлении параметров модели на основе новых наблюдений, что позволяет ей отслеживать изменения в распределении данных и сохранять точность прогнозов. Эффективные стратегии адаптации позволяют моделям избегать снижения производительности, вызванного несоответствием между моделью и текущей реальностью, и обеспечивают стабильную работу в условиях нестабильности.
Оценка апостериорного распределения (Posterior Distribution Estimation) представляет собой математически обоснованный подход к обновлению параметров модели на основе поступающих новых наблюдений. В отличие от методов, использующих точечные оценки, данный подход позволяет получить распределение вероятностей параметров, отражающее неопределенность в их значениях. Это достигается путем применения теоремы Байеса, комбинирующей априорное распределение (предварительные знания о параметрах) с функцией правдоподобия (вероятностью получения наблюдаемых данных при заданных параметрах). Полученное апостериорное распределение p(\theta|D), где θ — параметры, а D — данные, используется для вычисления оценок параметров, учитывающих как априорную информацию, так и новые наблюдения, что обеспечивает более надежные и точные прогнозы в изменяющихся условиях.
Для адаптации моделей к изменяющимся условиям используются различные методы исследования адаптированного пространства параметров, включая случайную реинициализацию, адаптацию на основе архивов и передачу информации на основе нейронных сетей (NNIT). Предложенный PosEDO (Posterior-based Evolutionary Dynamics Optimization) фреймворк демонстрирует превосходство над базовыми EDO (Evolutionary Dynamics Optimization) методами, показывая стабильно более низкие значения средней ошибки калибровки (MCE) на 18 тестовых примерах — 9 на наборе данных Brock-Hommes и 9 на PGPS (Parameter Gradient Propagation Simulator). Это указывает на повышенную эффективность PosEDO в поддержании точности прогнозов при изменении динамики системы.
Эволюционная Динамическая Оптимизация: Когда Модель «Эволюционирует» Вместе с Миром
Эволюционная динамическая оптимизация (ЭДО) представляет собой инновационный подход, объединяющий мощь эволюционных алгоритмов (ЭА) с механизмами обнаружения изменений и адаптации к окружающей среде. В отличие от традиционных методов оптимизации, предполагающих статичные параметры, ЭДО непрерывно отслеживает динамику системы и корректирует свою стратегию в ответ на изменения. Данный подход позволяет ЭДО эффективно функционировать в сложных и непредсказуемых условиях, где стандартные ЭА могут столкнуться с проблемами сходимости или застрять в локальных оптимумах. Благодаря интеграции механизмов обнаружения изменений, ЭДО способна быстро реагировать на новые тенденции и адаптироваться к изменяющимся требованиям, обеспечивая более устойчивые и эффективные решения для широкого спектра задач, включая моделирование финансовых рынков и управление сложными системами.
Эволюционная динамическая оптимизация (ЭДО) представляет собой эффективный подход к моделированию динамических систем, благодаря постоянной калибровке параметров и адаптации к изменяющимся условиям. В отличие от традиционных методов, которые часто полагаются на фиксированные параметры, ЭДО непрерывно оценивает и корректирует свои настройки, обеспечивая устойчивость и высокую производительность даже в сложных и непредсказуемых средах. Этот процесс адаптации позволяет ЭДО эффективно отслеживать изменения в системе и быстро реагировать на них, минимизируя ошибки и максимизируя точность прогнозов. Таким образом, ЭДО не просто описывает текущее состояние системы, но и предсказывает её будущее поведение, что делает его незаменимым инструментом для анализа и управления сложными процессами.
Модель Брока и Гоммеса служит ярким примером сложной динамической системы, где применение эволюционной динамической оптимизации (EDO) демонстрирует свою эффективность в реалистичных условиях. Эта модель, имитирующая поведение финансовых рынков с гетерогенными агентами, характеризуется нелинейностью и способностью к возникновению циклов и хаотических паттернов. Использование EDO позволяет алгоритму адаптироваться к постоянно меняющимся условиям рынка, оптимизируя стратегии агентов и обеспечивая более точное моделирование их поведения. В отличие от традиционных методов, которые часто требуют предварительного знания структуры модели или фиксированных параметров, EDO способен самообучаться и находить оптимальные решения даже в условиях высокой неопределенности и нелинейности, что делает его ценным инструментом для анализа и прогнозирования сложных экономических систем.
Для повышения эффективности адаптации в рамках эволюционной динамической оптимизации (EDO) применяются современные методы, такие как Маскированный Авторегрессионный Поток (MAF). Данный подход позволяет более точно оценивать распределения параметров, что критически важно для работы с динамически меняющимися системами. В частности, алгоритм PosEDO демонстрирует статистически значимое снижение среднеквадратичной ошибки (MCE) в большинстве тестовых случаев и характеризуется более низкими значениями PCON — показателя вычислительных затрат. Это свидетельствует о том, что PosEDO не только быстрее сходится к оптимальному решению, но и обеспечивает более стабильную работу в сравнении с традиционными алгоритмами, что делает его перспективным инструментом для моделирования сложных экономических и финансовых систем.
![Анализ точности обнаружения изменений на примере экземпляра [latex]F_8[/latex] модели Брока-Гоммеса показал, что точность существенно различается в зависимости от выбранного порога [latex] \varepsilon [/latex], при низких значениях ([latex] \varepsilon = 5, 15, 30 [/latex]) и высоких ([latex] \varepsilon = 100, 120 [/latex]), что позволяет оценить оптимальный порог для конкретной задачи.](https://arxiv.org/html/2601.19481v1/img2.png)
Наблюдая за стремлением к совершенству в калибровке социальных симуляций, представленном в работе, вспоминается высказывание Эдсгера Дейкстры: «Программирование — это не столько о создании программ, сколько об управлении сложностью». Попытки точно настроить модели, используя методы вроде PosEDO, демонстрируют, как быстро элегантная теория сталкивается с жестокой реальностью производственной среды. Улучшение онлайн-калибровки, основанное на апостериорных распределениях, — это, по сути, попытка хоть как-то обуздать эту сложность, отсрочить неизбежный технический долг, который накапливается в любом нетривиальном проекте. Ведь каждая новая оптимизация — это лишь временное облегчение, а не окончательное решение.
Что дальше?
Представленный подход, использующий апостериорные распределения для калибровки сложных социальных симуляций, несомненно, добавляет ещё один слой сложности в и без того непростую задачу. Однако, иллюзия «онлайн» калибровки, как показывает опыт, часто сталкивается с суровой реальностью дрифта данных и изменения динамики модели. Красивые графики, демонстрирующие сходимость, неизбежно превратятся в монолитные системы, требующие постоянного внимания и ручной корректировки. Вопрос не в том, улучшится ли калибровка, а в том, насколько быстро станет очевидным, что новые параметры просто замаскировали старые проблемы.
В перспективе, наиболее интересным представляется не совершенствование алгоритмов оптимизации, а разработка методов для оценки надёжности самой симуляции. Если тесты показывают зелёный свет — это, скорее всего, означает, что они попросту ничего не проверяют. Необходимы метрики, способные выявлять структурные недостатки модели и предсказывать её поведение в условиях, выходящих за рамки тестового набора. В противном случае, все эти ухищрения с апостериорными распределениями — лишь способ отложить неизбежное столкновение с реальностью.
И, конечно, стоит помнить, что «бесконечная масштабируемость» — это мантра, которую мы уже слышали в 2012-м году, только под другим названием. В конечном счёте, любой алгоритм упрётся в ограничения вычислительных ресурсов и необходимость компромиссов между точностью и скоростью. Поэтому, прежде чем строить воздушные замки, стоит задаться вопросом: а действительно ли нам нужна ещё более сложная модель, или достаточно просто признать её ограничения?
Оригинал статьи: https://arxiv.org/pdf/2601.19481.pdf
Связаться с автором: https://www.linkedin.com/in/avetisyan/
Смотрите также:
- Стоит ли покупать фунты за йены сейчас или подождать?
- МосБиржа на пути к 2800: Что поддерживает рост и как цифровизация влияет на рынок (26.01.2026 02:32)
- Российский рынок: рубль, микроэлектроника и дивидендные сюрпризы – что ждать инвестору? (23.01.2026 01:32)
- АбрауДюрсо акции прогноз. Цена ABRD
- Серебро прогноз
- Золото против Bitcoin: Почему «Цифровое Золото» Теряет Блеск? (29.01.2026 01:45)
- ТГК-2 префы прогноз. Цена TGKBP
- Европлан акции прогноз. Цена LEAS
- Прогноз нефти
- Российский рынок акций: Ожидание Давоса, отчетность лидеров и переток в металлы (20.01.2026 10:33)
2026-01-28 18:21