Адаптивный Бэйесовский Подход к Регрессии

Автор: Денис Аветисян

Новая методика позволяет повысить точность и эффективность анализа данных в обобщенных линейных моделях.

В рамках байесовской логистической регрессии, анализ апостериорных плотностей регрессионных коэффициентов, полученных при использовании стандартного нормального априорного распределения [latex]\beta_j \sim N(0,1)[/latex] для [latex]j = 1, 2, ..., 10[/latex], демонстрирует вариативность оценок коэффициентов и их распределение после учета данных. — В рамках байесовской логистической регрессии, анализ апостериорных плотностей регрессионных коэффициентов, полученных при использовании стандартного нормального априорного распределения $\beta_j \sim N(0,1)$ для $j = 1, 2, ..., 10$ , демонстрирует вариативность оценок коэффициентов и их распределение после учета данных.

Представлен гибкий вариационный подход к эмпирическому байесовскому анализу обобщенных линейных моделей, ориентированный на разреженную логистическую регрессию.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Традиционные подходы к построению байесовских обобщенных линейных моделей часто требуют трудоемкой настройки априорных распределений. В данной работе, посвященной ‘A Flexible Empirical Bayes Approach to Generalized Linear Models, with Applications to Sparse Logistic Regression’, предложен новый вариационно-байесовский метод, автоматически оценивающий априорное распределение непосредственно в процессе оптимизации. Этот подход, оптимизирующий среднее апостериорное распределение и параметры априорного, позволяет достичь высокой эффективности и применимости к широкому классу экспоненциальных семейств распределений, особенно в задачах разреженной логистической регрессии. Сможет ли предложенный метод стать универсальной альтернативой существующим вариационно-байесовским алгоритмам и открыть новые возможности для анализа сложных данных?

Разреженность: Поиск Истинных Связей в Хаосе Данных

В многочисленных статистических задачах часто возникает необходимость выделить небольшое количество действительно важных переменных из обширного набора данных. Этот процесс, известный как разреженное моделирование, представляет собой поиск наиболее значимых факторов, определяющих исследуемое явление. Вместо того чтобы учитывать все переменные, что может привести к избыточности и снижению точности, разреженное моделирование фокусируется на выявлении ключевых предикторов. Такой подход не только упрощает модели, делая их более понятными и интерпретируемыми, но и повышает их обобщающую способность, особенно в случаях, когда количество переменных значительно превышает объем доступных данных. Эффективное выявление этих важных переменных позволяет создавать более надежные прогнозы и лучше понимать лежащие в основе закономерности.

Традиционные методы статистического моделирования часто сталкиваются с серьезными трудностями при работе с данными высокой размерности. Когда количество переменных значительно превышает объем имеющихся наблюдений, стандартные алгоритмы склонны к переобучению — ситуации, когда модель слишком хорошо адаптируется к обучающей выборке, но теряет способность к обобщению на новые данные. Это проявляется в ложноположительных результатах и ненадёжных прогнозах. Кроме того, высокая размерность усложняет выявление истинных закономерностей, поскольку шум и случайные колебания могут маскировать важные сигналы, приводя к неточным оценкам параметров и ухудшению общей производительности модели. Подобные ограничения подчеркивают необходимость разработки новых подходов, способных эффективно справляться с задачами в условиях ограниченных данных и большого количества переменных.

Эффективная разреженная оценка имеет решающее значение для точного прогнозирования и создания интерпретируемых моделей в самых разных областях. В ситуациях, когда количество переменных значительно превышает количество наблюдений, или когда большинство переменных не оказывают существенного влияния на результат, традиционные методы статистического анализа часто дают неточные или ненадежные результаты. Разреженное моделирование позволяет выделить лишь наиболее важные факторы, что приводит к повышению точности прогнозов и снижению риска переобучения. Более того, простота, достигаемая за счет использования небольшого числа переменных, облегчает понимание модели и позволяет исследователям и специалистам извлекать значимые выводы из данных, что особенно важно в таких областях, как геномика, обработка изображений и финансовый анализ. Таким образом, разреженное моделирование является не просто статистическим приемом, а мощным инструментом для извлечения знаний и принятия обоснованных решений.

Методы, основанные на EBGLM, демонстрируют стабильно более высокую AUC в различных симуляциях, варьирующих размер выборки [latex]n[/latex], размерность [latex]p[/latex], корреляцию ρ между признаками, уровень разреженности [latex]s[/latex] и распределение истинных коэффициентов, что подтверждает их надежность в различных условиях. — Методы, основанные на EBGLM, демонстрируют стабильно более высокую AUC в различных симуляциях, варьирующих размер выборки $n$ , размерность $p$ , корреляцию ρ между признаками, уровень разреженности $s$ и распределение истинных коэффициентов, что подтверждает их надежность в различных условиях.

Байесовские Основы Разреженности: Вероятностный Подход к Выбору

Байесовские методы предоставляют естественную основу для разреженного оценивания, поскольку они включают априорные убеждения о параметрах модели и количественно оценивают неопределенность. В отличие от классических методов, которые полагаются на точечные оценки параметров, байесовский подход рассматривает параметры как случайные величины, описываемые априорным распределением. Это позволяет учитывать предшествующие знания о структуре данных и, в частности, о вероятности того, что определенные параметры могут быть равны нулю. Количественная оценка неопределенности достигается через апостериорное распределение, которое объединяет априорные убеждения с информацией, полученной из данных, предоставляя не только оценки параметров, но и меру их достоверности. Такой подход особенно полезен в задачах, где важно выявить наиболее значимые признаки и исключить незначимые, что и является сутью разреженного моделирования.

Выбор априорного распределения играет ключевую роль в байесовской оценке разреженных моделей, напрямую влияя на степень разреженности полученных оценок и стабильность модели. Различные априорные распределения задают различные вероятности для значений параметров модели, что определяет, насколько вероятно, что определенный коэффициент будет равен нулю или близок к нему. Более сильные априорные распределения, смещенные к нулю, приводят к более разреженным решениям, но могут привести к недооценке значимых эффектов. Напротив, более слабые априорные распределения допускают большее количество ненулевых коэффициентов, обеспечивая большую гибкость, но потенциально приводя к переобучению. Таким образом, выбор априорного распределения требует тщательного баланса между стремлением к разреженности и необходимостью адекватного представления данных.

Априорные распределения, такие как Horseshoe Prior и Spike-and-Slab Prior, обеспечивают непрерывное уменьшение (shrinkage) коэффициентов модели, что способствует разреженности. В отличие от жестких порогов, используемых в некоторых методах регуляризации, эти априорные распределения позволяют коэффициентам постепенно приближаться к нулю, потенциально устанавливая их в точности равными нулю. При этом они сохраняют возможность моделирования значимых, отличных от нуля эффектов, обеспечивая гибкость и адаптивность к данным. Horseshoe Prior характеризуется тяжелыми хвостами, что позволяет коэффициентам принимать широкий диапазон значений, в то время как Spike-and-Slab Prior комбинирует точечное распределение (spike) в нуле и непрерывное распределение (slab) для ненулевых значений, эффективно моделируя разреженность и не разреженность одновременно.

Традиционные методы регуляризации, такие как L1- и L2-регуляризация, часто полагаются на фиксированные штрафы для достижения разреженности модели. Однако, эти подходы могут потребовать ручной настройки гиперпараметров для оптимального баланса между сложностью модели и соответствием данным. В отличие от них, априорные распределения, такие как Horseshoe и Spike-and-Slab, обеспечивают автоматический, основанный на вероятностных принципах, способ достижения этого баланса. Эти априорные распределения позволяют коэффициентам модели естественным образом стремиться к нулю, эффективно осуществляя отбор признаков, при этом сохраняя возможность моделировать значимые не-нулевые эффекты. Это достигается за счет использования вероятностных моделей, которые адаптируются к данным, обеспечивая более гибкое и надежное решение, чем фиксированные штрафы, и избегая необходимости в кросс-валидации для выбора оптимального параметра регуляризации.

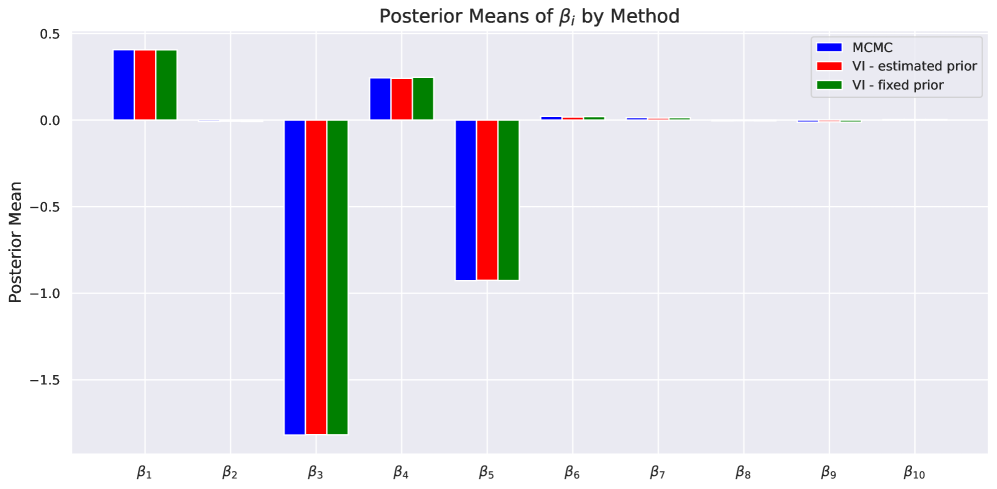
В байесовской логистической регрессии, при нормальном априорном распределении коэффициентов <span class="katex-eq" data-katex-display="false">eta\_{j}\sim 0.5\delta\_{0}+0.5N(0,1)</span> и нулевой корреляции между признаками <span class="katex-eq" data-katex-display="false">
ho=0</span>, наблюдается соответствие между маргинальными вариационными апостериорными плотностями и апостериорными средними значениями регрессионных коэффициентов. — В байесовской логистической регрессии, при нормальном априорном распределении коэффициентов $eta\_{j}\sim 0.5\delta\_{0}+0.5N(0,1)$ и нулевой корреляции между признаками $ho=0$ , наблюдается соответствие между маргинальными вариационными апостериорными плотностями и апостериорными средними значениями регрессионных коэффициентов.

EBGLM: Эмпирический Байесовский Подход к Разреженной Регрессии

Предложенная Эмпирическая Байесовская Обобщенная Линейная Модель (EBGLM) представляет собой практическое решение для разреженной регрессии, объединяя преимущества байесовского моделирования и эмпирической байесовской оценки. В отличие от традиционных методов, EBGLM не требует предварительного задания фиксированного априорного распределения для параметров модели. Вместо этого, априорное распределение оценивается непосредственно на основе данных, что позволяет модели адаптироваться к особенностям конкретного набора данных и повысить точность предсказаний. Комбинация байесовского подхода, позволяющего учитывать неопределенность в оценках параметров, и эмпирической байесовской оценки, обеспечивающей вычислительную эффективность, делает EBGLM особенно полезным в задачах с высокой размерностью и разреженностью данных.

В основе EBGLM лежит метод вариационного вывода (Variational Inference), позволяющий аппроксимировать апостериорное распределение параметров модели. В отличие от методов Монте-Карло Маркова, требующих большого количества выборок, вариационный вывод преобразует сложную задачу вычисления апостериорного распределения в оптимизационную задачу. Это достигается путем поиска распределения, которое является наиболее близким к истинному апостериорному в смысле расхождения Кульбака-Лейблера. Такой подход значительно снижает вычислительные затраты, особенно в задачах со многими признаками (высокоразмерных пространствах), делая EBGLM эффективным инструментом для разреженного регрессионного анализа.

Для оптимизации целевой функции в рамках EBGLM используется алгоритм L-BFGS (Limited-memory Broyden-Fletcher-Goldfarb-Shanno). L-BFGS является квазиньютоновским методом, эффективно аппроксимирующим матрицу Гессе, что позволяет избежать явного хранения и обращения этой матрицы, что критично при работе с данными высокой размерности. Алгоритм использует ограниченный объем памяти для хранения информации о градиентах, что обеспечивает быструю сходимость и надежную работу даже при большом количестве признаков и параметров модели. Практическая реализация L-BFGS в EBGLM гарантирует стабильную сходимость к локальному минимуму целевой функции, что подтверждается эмпирическими результатами и сравнительными анализами с другими методами регуляризации.

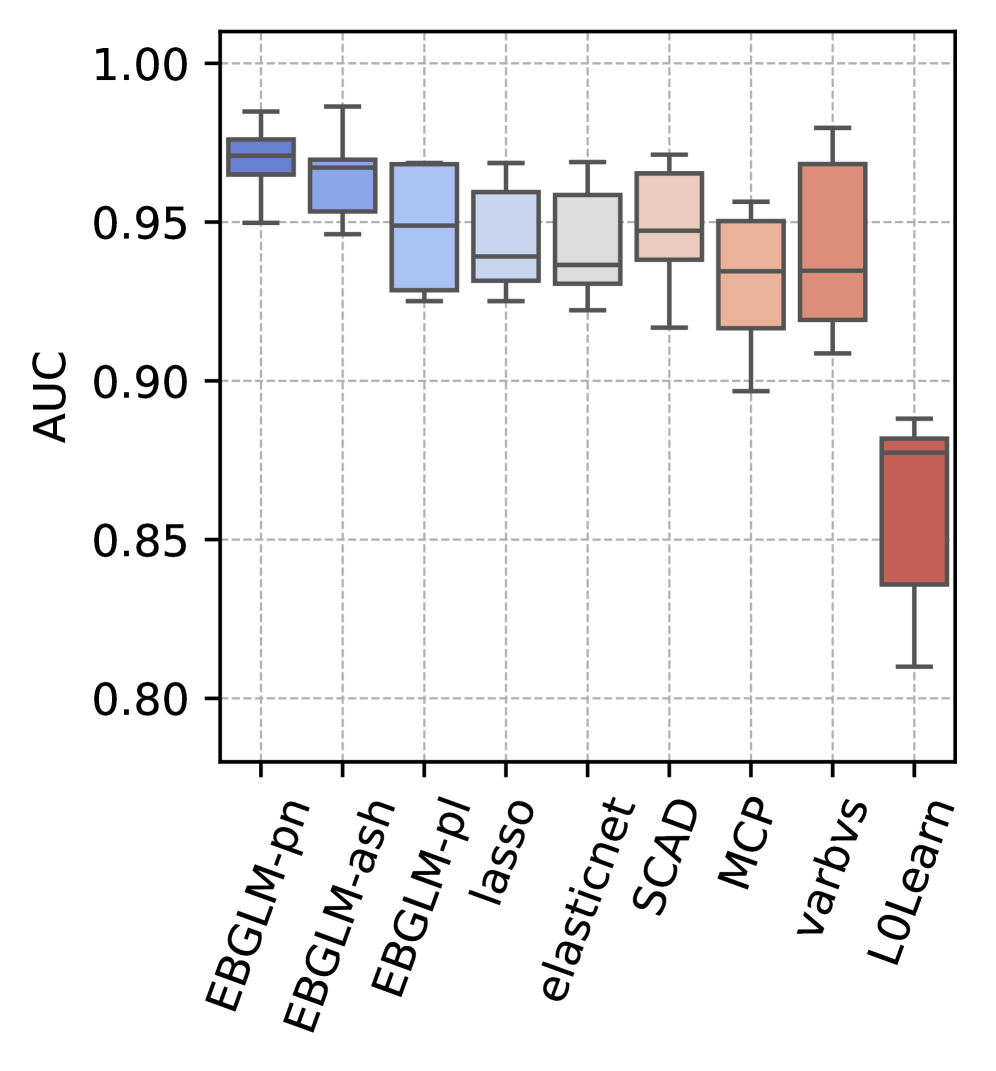
В рамках EBGLM адаптивная оценка априорного распределения на основе данных позволяет добиться более высоких значений метрики AUC по сравнению с методами Lasso, Ridge Regression, Elastic Net, SCAD, MAD, L0Learn, varbvs и sparsevb. В отличие от традиционных методов регуляризации, использующих фиксированные априорные распределения, EBGLM динамически оценивает параметры этих распределений непосредственно из данных, что обеспечивает более точную настройку модели и, как следствие, улучшенные показатели классификации. Проведенные эксперименты демонстрируют устойчивое превосходство EBGLM по AUC на различных наборах данных, подтверждая эффективность предложенного подхода к разреженному регрессионному анализу.

Методы на основе EBGLM демонстрируют более высокую медианную AUC и меньшую дисперсию по сравнению с другими подходами при классификации документов из набора данных 20 Newsgroups, что указывает на их высокую предсказательную способность и устойчивость в задачах классификации текстов высокой размерности.

Уточнение Разреженности с Продвинутыми Априорными Распределениями: Гибкость и Адаптивность

В рамках EBGLM предусмотрена гибкая настройка за счет совместимости с различными непрерывными априорными распределениями, выполняющими функцию усадки коэффициентов. Среди них — $R^2D^2$ Prior, Point Normal Prior и Point Laplace Prior. Использование этих априорных распределений позволяет исследователям адаптировать модель к специфике данных и поставленной задаче, контролируя степень усадки коэффициентов и, следовательно, сложность и интерпретируемость модели. В отличие от фиксированных штрафов, применяемых в традиционных методах, таких как Lasso или Ridge регрессия, непрерывные априорные распределения EBGLM обеспечивают более тонкую настройку и потенциально улучшают точность предсказаний и выбор наиболее значимых переменных.

В сравнении с общепринятыми методами, такими как $Lasso$ , $Ridge Regression$ и $Elastic Net$ , разработанный EBGLM зачастую демонстрирует превосходную прогностическую способность и более точный отбор переменных. Это достигается благодаря адаптивному сокращению коэффициентов, которое позволяет модели эффективно выявлять наиболее значимые факторы, игнорируя шум и избыточные данные. В результате, предсказания, полученные с использованием EBGLM, отличаются большей точностью, а отобранные переменные лучше отражают истинные взаимосвязи в данных, что особенно важно при анализе сложных систем и принятии обоснованных решений.

Адаптивное сокращение коэффициентов в рамках данной модели обеспечивает повышенную устойчивость и интерпретируемость результатов, особенно в ситуациях, когда данные содержат значительный шум или демонстрируют высокую корреляцию между переменными. В отличие от традиционных методов, которые применяют фиксированные штрафы, данная модель динамически регулирует степень сокращения для каждого коэффициента, позволяя более точно отделить значимые сигналы от случайных колебаний. Это особенно важно при анализе сложных наборов данных, где коррелированные предикторы могут приводить к ложноположительным результатам или неточному определению наиболее важных факторов. Благодаря этому подходу, модель способна строить более надежные и понятные прогнозы, а также предоставлять более точную информацию о взаимосвязях между переменными.

Исследования показали, что разработанная методика EBGLM демонстрирует высокую устойчивость к изменениям в условиях моделирования. Проведенные эксперименты охватывают широкий спектр параметров: от небольших выборок, содержащих 200 наблюдений, до крупных, включающих 3000, а также от низкоразмерных данных с 20 признаками до высокоразмерных с 3000. Устойчивость сохраняется при различных уровнях разреженности — от единичных значимых признаков до 300, и даже в условиях сильной корреляции между переменными, варьирующейся от полного отсутствия связи до почти полной зависимости (коэффициент корреляции ρ = 0-0.99). Такая универсальность позволяет использовать EBGLM в самых разных задачах анализа данных, гарантируя надежные результаты независимо от специфики исходного набора данных.

Сравнение штрафных функций показывает, что выбор гиперпараметров [latex]\pi_{0}[/latex] и [latex]\sigma^{2}[/latex] в априорном распределении Point Normal позволяет контролировать степень уменьшения коэффициентов, аналогично тому, как это делают известные методы регуляризации в регрессионном анализе. — Сравнение штрафных функций показывает, что выбор гиперпараметров $\pi_{0}$ и $\sigma^{2}$ в априорном распределении Point Normal позволяет контролировать степень уменьшения коэффициентов, аналогично тому, как это делают известные методы регуляризации в регрессионном анализе.

Наблюдается закономерность: стремление к гибкости в построении моделей, как это демонстрируется в предложенном подходе вариационного вывода для обобщенных линейных моделей, неизбежно ведёт к усложнению системы. Этот процесс напоминает рост живого организма, где каждая адаптация, каждое усовершенствование добавляет новые слои взаимосвязей. Юрген Хабермас однажды заметил: «Коммуникативное действие — это не просто обмен информацией, а процесс взаимного понимания и согласования действий». Аналогично, и в данной работе, ключевым является не просто достижение разреженности регрессии, но и обеспечение возможности самонастройки модели, её способности адаптироваться к новым данным и условиям. Система, лишенная этой способности к коммуникации и самообучению, обречена на стагнацию и, в конечном счете, на крах.

Что дальше?

Представленная работа, словно тщательно выращенный саженец, демонстрирует изящный подход к построению обобщённых линейных моделей. Однако, не стоит забывать, что даже самый ухоженный сад нуждается в постоянном внимании. Авторы предлагают гибкий инструмент для разреженного регрессионного анализа, но сама гибкость — это всегда обещание будущих компромиссов. Каждый архитектурный выбор, каждая оптимизация — это своего рода пророчество о потенциальной точке отказа, о тех случаях, когда модель перестанет прощать ошибки в данных.

Будущие исследования, вероятно, сосредоточатся на преодолении границ применимости данной структуры. Необходимо учитывать, что вариационный вывод — это лишь приближение, а истинный байесовский вывод остаётся недостижимым идеалом. Поэтому, особое внимание следует уделить разработке более точных и эффективных методов аппроксимации, способных справиться с задачами, где данные особенно сложны и неоднородны. Важно помнить, что система — это не машина, которую можно собрать, а сад, который нужно взращивать.

В конечном счёте, успех подобного подхода будет зависеть не только от математической элегантности, но и от способности адаптироваться к реальным проблемам. Необходимо исследовать возможности интеграции с другими моделями и алгоритмами, а также разработать инструменты для автоматической диагностики и исправления ошибок. Ведь устойчивость — это не изоляция компонентов, а их способность прощать ошибки друг друга.

Оригинал статьи: https://arxiv.org/pdf/2601.21217.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-31 01:47