Адаптивный поиск: новый подход к оптимизации сложных систем

Автор: Денис Аветисян

В статье представлена методика, позволяющая эффективно находить оптимальные решения в задачах, где характеристики среды меняются со временем.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал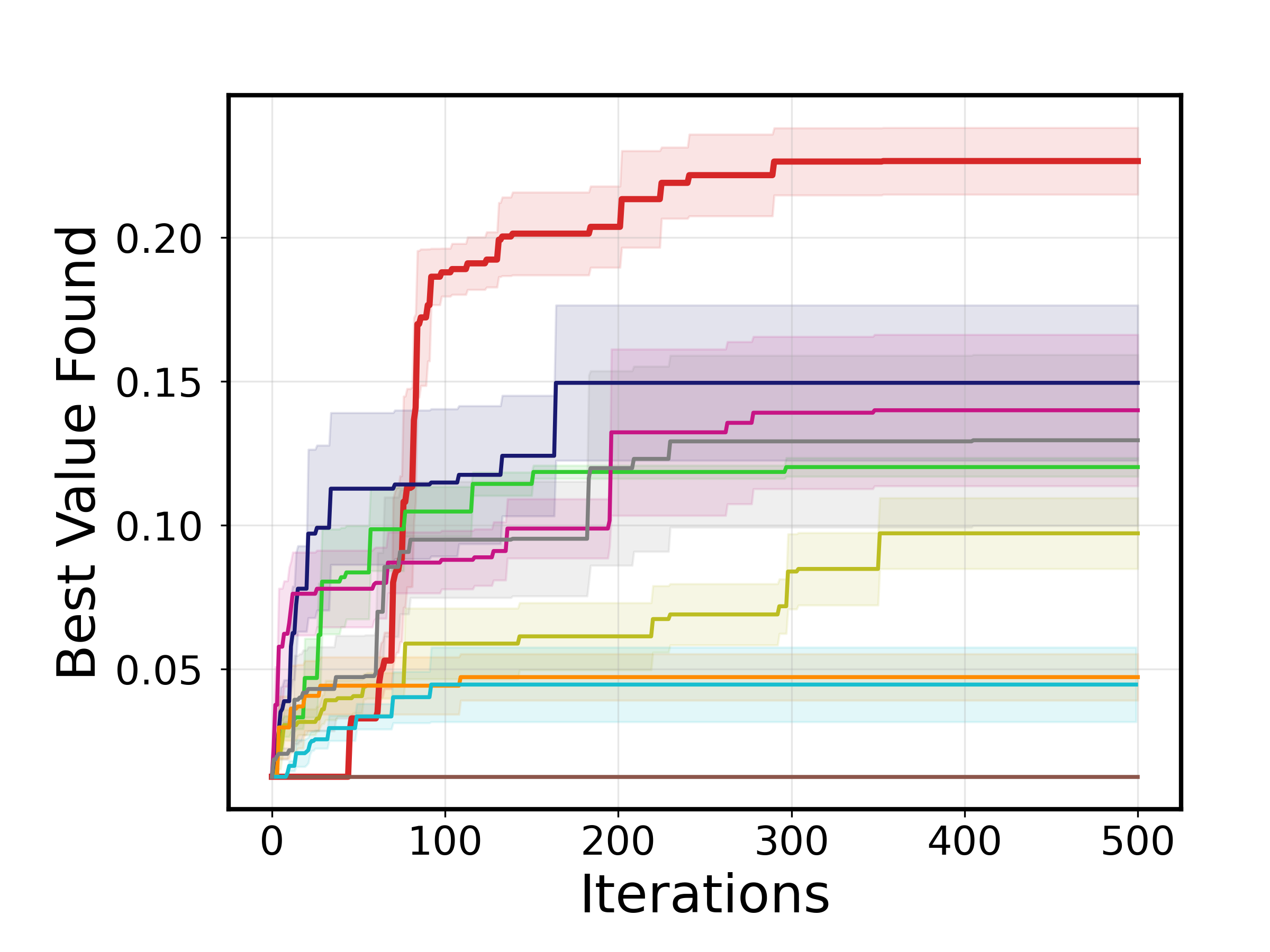

Алгоритм RAMBO демонстрирует превосходство над существующими подходами в задачах оптимизации, как на синтетических (функции Леви и Швефеля в 6D и 10D), так и на реальных данных (оптимизация молекулярных конформаций в 12D, виртуальный скрининг для разработки лекарств в 50D и проектирование стеллараторных реакторов в 81D), особенно эффективно справляясь с многомерными и многорежимными ландшафтами.

Разработан фреймворк RAMBO, использующий смесь гауссовских процессов и модель Дирихле для адаптивной оптимизации в нестанционарных задачах.

Стандартные методы байесовской оптимизации часто сталкиваются с трудностями при работе с негладкими функциями, имеющими несколько режимов. В данной работе, посвященной ‘Regime-Adaptive Bayesian Optimization via Dirichlet Process Mixtures of Gaussian Processes’, предложен новый подход RAMBO, использующий смесь гауссовских процессов с дирихлетовским процессом для адаптивного моделирования сложных ландшафтов оптимизации. Это позволяет автоматически выявлять скрытые режимы и эффективно исследовать пространство поиска, обеспечивая превосходство над существующими методами в задачах, таких как оптимизация молекулярных конформаций и разработка лекарств. Способна ли данная методика существенно расширить границы применимости байесовской оптимизации в других областях науки и техники?

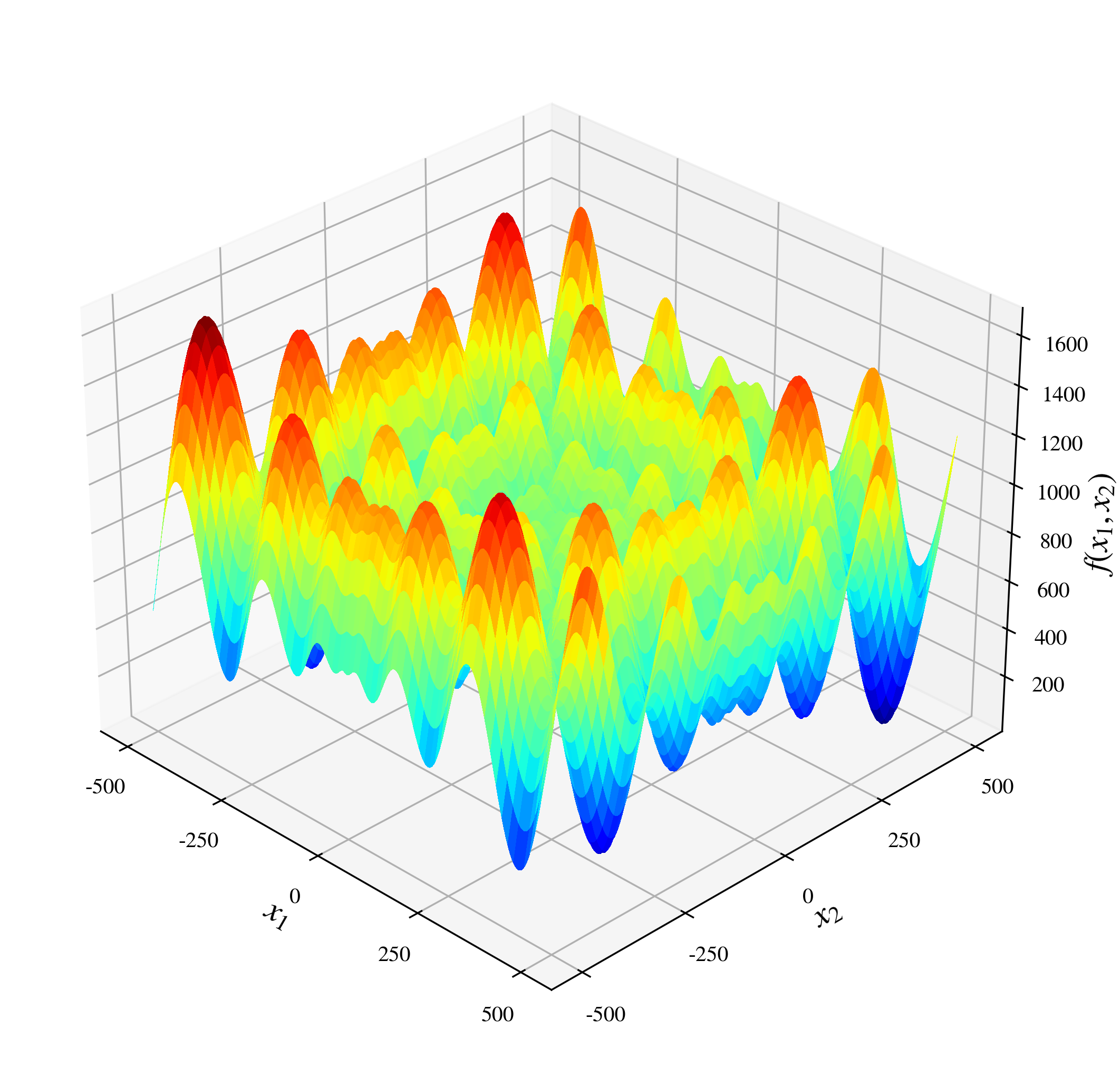
Нестационарность оптимизации: вызов сложности

Многие задачи оптимизации, возникающие в реальном мире, характеризуются нестационарностью — свойством, при котором характеристики целевой функции меняются в зависимости от исследуемой области поиска. Это означает, что традиционные методы оптимизации, предполагающие постоянство свойств функции, оказываются неэффективными. Например, в задачах, связанных с динамическими системами или машинным обучением, оптимальное решение может меняться со временем или в зависимости от входных данных. Такая изменчивость требует разработки новых подходов, способных адаптироваться к меняющемуся ландшафту целевой функции и эффективно находить оптимальные решения даже в условиях неопределенности. Попытки применить стандартные алгоритмы к нестационарным задачам часто приводят к замедлению сходимости, застреванию в локальных оптимумах или, в конечном итоге, к неспособности найти удовлетворительное решение.

Стандартные гауссовские процессы, использующие стационарные ядра, испытывают трудности при моделировании сложных оптимизационных ландшафтов. Проблема заключается в том, что стационарные ядра предполагают неизменность характеристик функции по всему пространству поиска, что редко соответствует действительности в реальных задачах. В результате, предсказания, основанные на таких моделях, оказываются неточными, особенно в областях, где функция резко меняется или имеет несколько локальных оптимумов. Это приводит к неэффективному исследованию пространства поиска и снижает вероятность нахождения глобального оптимума, поскольку модель не способна адекватно оценить неопределенность и направить поиск в перспективные области. Вместо точных оценок, процесс оптимизации рискует застрять в локальных минимумах или тратить ресурсы на бесперспективные участки пространства.

Особую сложность в задачах не стационарной оптимизации представляет наличие множественных локальных оптимумов. В подобных задачах, пространство поиска усеяно точками, где функция достигает максимума или минимума, однако лишь одна из них является глобальным. Традиционные алгоритмы оптимизации, стремясь к быстрому улучшению, часто застревают в ближайшем локальном оптимуме, не в состоянии обнаружить более выгодное глобальное решение. Это затрудняет поиск действительно наилучшей точки, поскольку алгоритм может ошибочно принять локальный оптимум за глобальный, что приводит к субоптимальным результатам и снижению эффективности решения поставленной задачи. Сложность поиска глобального оптимума возрастает экспоненциально с увеличением размерности пространства поиска и количества локальных оптимумов.

Трехмерный график функции Швефеля демонстрирует наличие множества локальных оптимумов, затрудняющих поиск изолированного глобального минимума.

DPMM-GP: адаптивная суррогатная модель

Модель DPMM-GP (Dirichlet Process Mixture of Gaussian Processes) представляет собой эффективный подход к построению суррогатных моделей, основанный на разбиении пространства поиска на отдельные “режимы”. Каждый из этих режимов моделируется собственной Гауссовой функцией $GP(x)$ . Такое разделение позволяет более точно аппроксимировать сложные функции, особенно в случаях, когда зависимость между входными и выходными данными неоднородна. Фактически, DPMM-GP автоматически определяет границы между этими режимами, адаптируясь к структуре данных и обеспечивая высокую точность предсказаний в различных областях пространства поиска.

Дирихле-процесс (Dirichlet Process) позволяет динамически определять количество и границы режимов в пространстве поиска, что критически важно для адаптации к нестационарности. В отличие от фиксированного разбиения, Дирихле-процесс автоматически регулирует сложность модели, добавляя или объединяя режимы в зависимости от наблюдаемых данных. Это достигается путем использования непараметрической априорной вероятности, которая определяет распределение вероятностей по всем возможным разбиениям пространства поиска. Вероятность конкретного разбиения определяется как бесконечное произведение, учитывающее как количество режимов, так и их размеры. Такой подход позволяет модели адаптироваться к изменяющимся характеристикам оптимизируемой функции, не требуя явного задания количества режимов или их границ заранее.

Модель DPMM-GP обеспечивает надежное и точное приближение, объединяя сильные стороны гауссовских процессов (GP) и процессов Дирихле (DP). Гауссовские процессы эффективно моделируют сложные функции, предоставляя вероятностные прогнозы с оценкой неопределенности. Однако, стандартные GP испытывают трудности при работе с не стационарными данными. Процесс Дирихле позволяет динамически адаптировать сложность модели, автоматически определяя оптимальное количество компонентов смеси и их границы. В DPMM-GP, каждый компонент смеси моделируется отдельным гауссовским процессом, что позволяет моделировать различные режимы поведения в данных и повышает общую точность и устойчивость модели к изменениям в данных. $\mathbb{G} \sim \text{DP}(\alpha, H)$ определяет априорное распределение над распределениями, где α — параметр концентрации, а $H$ — базовое распределение.

Адаптивное планирование параметра концентрации

Для управления сложностью Дирихле-процесса и предотвращения переобучения используется адаптивное планирование параметра концентрации. Параметр концентрации, обозначаемый как α, контролирует вероятность того, что новый объект будет назначен существующему кластеру или создан новый. Адаптивное планирование позволяет изменять α в процессе обучения, начиная с более высокого значения, которое способствует образованию небольшого числа кластеров, и постепенно уменьшая его, что позволяет модели исследовать более гранулярные представления данных. Это динамическое изменение предотвращает как недообучение (слишком мало кластеров), так и переобучение (слишком много кластеров, приспособленных к шуму в обучающих данных), обеспечивая оптимальный баланс между сложностью модели и ее обобщающей способностью.

Для управления ростом числа режимов в процессе Дирихле и обеспечения баланса между исследованием (exploration) и использованием (exploitation) применяется схема LogSqrtSchedule. Данная схема предусматривает постепенное уменьшение концентрационного параметра, что позволяет количеству режимов увеличиваться со скоростью, пропорциональной $\sqrt{\log(t)}$ , где $t$ — текущая итерация обучения. Такой подход позволяет модели адаптироваться к сложности данных, избегая преждевременной сходимости к локальным оптимумам и одновременно ограничивая переобучение за счет контролируемого увеличения числа параметров.

Адаптивное изменение параметра концентрации позволяет модели эффективно исследовать сложные пространства параметров, минимизируя риск попадания в локальные оптимумы. Контролируемый рост числа режимов, обеспечиваемый данной методикой, снижает чувствительность к шумам и позволяет более надежно находить глобальные решения. Это приводит к повышению стабильности и скорости сходимости алгоритма оптимизации, особенно в задачах с невыпуклыми функциями потерь и большим количеством параметров. В результате, достигается улучшенная обобщающая способность модели и более высокая точность предсказаний на новых данных.

Оптимизация пространства, состоящего из 12 вращательных степеней свободы, осложняется сложными энергетическими барьерами, возникающими из-за стерических препятствий между атомами 11 и 44.

Вывод и применение к байесовской оптимизации

Метод коллапсирующего семплирования Гиббса оказался эффективным инструментом для проведения статистического вывода в модели DPMM-GP. Данный подход позволяет оценить апостериорное распределение режимов и параметров модели, что критически важно для понимания и прогнозирования поведения сложных систем. В рамках этого метода, вероятности принадлежности данных к различным режимам и соответствующие параметры модели оцениваются и обновляются итеративно, без необходимости явного вычисления нормализующей константы. Это значительно упрощает процесс вывода и повышает вычислительную эффективность, особенно в случаях с большим объемом данных и высокой размерностью пространства параметров. Полученное апостериорное распределение предоставляет полное представление о неопределенности в оценках, позволяя более надежно принимать решения и делать прогнозы.

Интеграция модели DPMM-GP в качестве суррогатной модели внутри алгоритма байесовской оптимизации позволяет эффективно оптимизировать дорогостоящие «черные ящики» — функции, внутреннее устройство которых неизвестно. Вместо прямой оценки целевой функции, требующей значительных вычислительных ресурсов или времени, DPMM-GP строит вероятностную модель, аппроксимирующую её поведение. Этот подход позволяет алгоритму байесовской оптимизации разумно выбирать следующие точки для оценки, направляя поиск в наиболее перспективные области пространства параметров и избегая ненужных вычислений. В результате достигается значительное ускорение процесса оптимизации, особенно в задачах, где каждое вычисление целевой функции является ресурсоемким, что делает данный метод применимым в широком спектре научных и инженерных дисциплин.

Комбинация модели DPMM-GP в рамках байесовской оптимизации демонстрирует повышенную устойчивость и надежность при решении задач оптимизации, даже в условиях нестационарности и наличия множественных локальных оптимумов. Проведенные эксперименты показывают, что предложенный подход превосходит традиционные методы, обеспечивая в среднем улучшение на 8.05% при оптимизации молекулярных конформаций, 4.06% в задачах разработки лекарственных препаратов и впечатляющий прирост в 51.55% при проектировании термоядерных реакторов. Такие результаты подчеркивают значительный потенциал данной комбинации для решения сложных и требовательных оптимизационных задач в различных областях науки и техники.

В представленной работе исследуется адаптивное байесовское оптимизирование, стремящееся к упрощению процесса поиска оптимальных решений в сложных, меняющихся ландшафтах. Авторы предлагают RAMBO — систему, использующую смесь гауссовских процессов, чтобы эффективно моделировать различные режимы оптимизации. Как отмечал Клод Шеннон: «Информация — это не столько содержание сообщения, сколько выбор из возможных сообщений». Аналогично, RAMBO не просто ищет оптимальное решение, а адаптируется к текущему ‘режиму’ пространства поиска, уменьшая неопределенность и фокусируясь на наиболее перспективных областях. Такой подход позволяет системе достигать лучших результатов, избегая избыточной сложности и сосредотачиваясь на существенном.

Куда Далее?

Представленная работа, хотя и демонстрирует определенный прогресс в адаптивной оптимизации, лишь подчеркивает сложность не стационарных ландшафтов. Упор на смесь гауссовских процессов с использованием процесса Дирихле, безусловно, является элегантным решением, но не решает фундаментальной проблемы: истинная природа “режимов” в высокоразмерных пространствах часто остается неясной. Полагаться на автоматическое обнаружение режимов — это все равно что искать порядок в хаосе, ожидая, что он сам себя проявит.

Будущие исследования, вероятно, должны сосредоточиться не столько на усовершенствовании алгоритмов, сколько на разработке более эффективных способов представления и структурирования информации о ландшафте оптимизации. Необходим переход от чисто адаптивных методов к более осознанным стратегиям исследования, включающим априорные знания и экспертные оценки. В конечном счете, оптимизация — это не только поиск минимума, но и понимание структуры пространства, в котором этот минимум находится.

Стремление к универсальному алгоритму, способному решить любую задачу оптимизации, представляется тщеславным. Гораздо продуктивнее признать ограниченность любого метода и сосредоточиться на разработке специализированных инструментов, адаптированных к конкретным областям применения. В этом, возможно, и заключается истинное милосердие — в ясности ограничений.

Оригинал статьи: https://arxiv.org/pdf/2601.20043.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-30 03:52