Быстрый расчёт сложных уравнений диффузии: новый подход

Автор: Денис Аветисян

В статье представлен эффективный численный метод для решения уравнений диффузии с неопределенностью, значительно снижающий вычислительные затраты.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал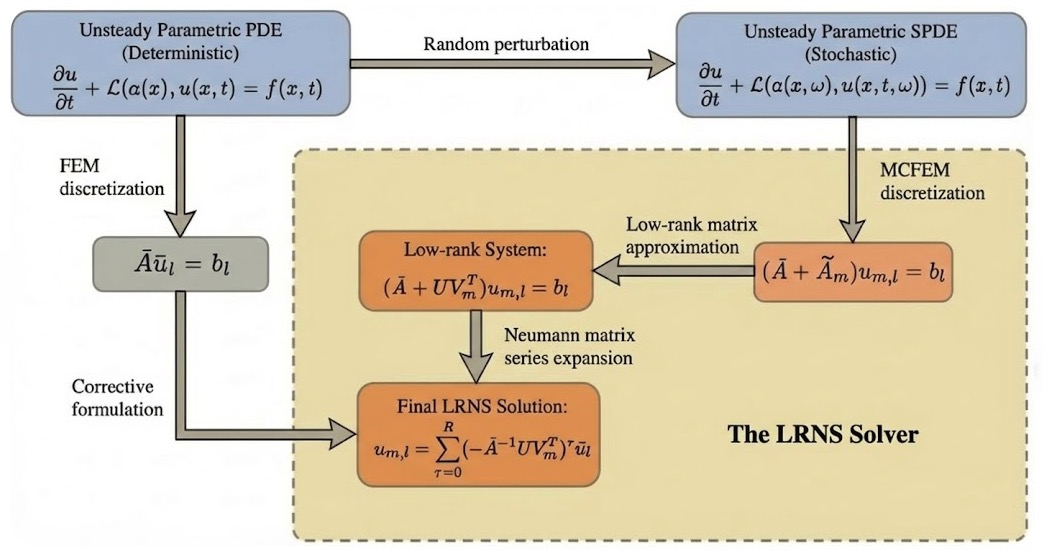

Эффективный решатель, представленный в виде блок-схемы, обеспечивает точное и надежное вычисление решения, опираясь на математически обоснованный алгоритм, гарантирующий корректность результата и исключающий возможность промежуточных состояний.

Предложен алгоритм LRNS, сочетающий аппроксимацию низким рангом и ряд Неймана для решения нестационарных стохастических уравнений диффузии и задач оптимального управления.

Решение нестационарных дифференциальных уравнений в частных производных с случайными коэффициентами часто сталкивается с вычислительными трудностями, связанными с обработкой масштабных линейных систем. В данной работе, посвященной ‘An efficient solver based on low-rank approximation and Neumann matrix series for unsteady diffusion-type partial differential equations with random coefficients’, предложен эффективный численный решатель, основанный на комбинации приближения низкоранговыми матрицами и разложением в ряд Неймана, для снижения вычислительных затрат и требований к памяти. Предложенный подход позволяет трансформировать инвертирование многомерных матриц в последовательность операций умножения низкоразмерных матриц, значительно повышая производительность. Возможно ли дальнейшее расширение области применения данного решателя для решения более сложных задач неопределенности и оптимального управления?

Математическая Элегантность Стохастических Уравнений

Решение стохастических дифференциальных уравнений в частных производных (СПДУ) играет фундаментальную роль в моделировании широкого спектра явлений в различных научных областях. От прогнозирования финансовых рынков и анализа турбулентности жидкости до моделирования распространения эпидемий и изучения климатических изменений — СПДУ предоставляют математический аппарат для описания систем, подверженных случайным воздействиям. Их применение простирается и на материаловедение, позволяя исследовать поведение материалов с дефектами, и на биологию, где они используются для моделирования динамики популяций и процессов клеточной диффузии. Эффективное решение СПДУ является ключевым фактором для получения точных и надежных результатов в этих и многих других областях науки и техники, что делает их изучение и разработку численных методов особенно актуальной задачей.

Традиционные методы решения стохастических дифференциальных уравнений в частных производных (SPDE), такие как метод Монте-Карло с применением конечных элементов (MC-FEM), часто сталкиваются с существенными вычислительными ограничениями. Эта проблема обусловлена тем, что для достижения приемлемой точности требуется экспоненциально большое количество выборок, особенно при увеличении размерности задачи и сложности стохастической модели. В результате, применение MC-FEM становится непрактичным для моделирования сложных явлений, требующих детального анализа, например, в задачах гидродинамики, материаловедения или финансовой математики. Необходимость в более эффективных алгоритмах, способных преодолеть эти вычислительные барьеры, является ключевой задачей в области численного моделирования SPDE и ограничивает возможности широкого применения этих уравнений для решения реальных научных и инженерных проблем.

Высокая размерность и стохастическая природа стохастических дифференциальных уравнений в частных производных (SPDE) создают значительные вычислительные трудности, особенно при моделировании крупномасштабных явлений. Традиционные численные методы часто оказываются непомерно затратными по ресурсам, что ограничивает их применение к задачам реального мира. Необходимость эффективных решателей обусловлена тем, что для точного моделирования SPDE требуется учитывать огромное количество случайных переменных и параметров, что приводит к экспоненциальному росту вычислительной сложности. Разработка алгоритмов, способных справляться с этими трудностями, является ключевой задачей для продвижения в областях, таких как финансовое моделирование, физика конденсированного состояния и климатология. Поиск компромисса между точностью и вычислительной эффективностью, а также использование параллельных вычислений и адаптивных методов, представляются наиболее перспективными направлениями исследований в этой области.

Снижение Вычислительной Сложности посредством Низкоранговых Приближений

Приближение матриц пониженной размерности (LRA) представляет собой эффективный метод снижения вычислительной нагрузки за счет замены исходных высокоразмерных матриц их низкоранговыми представлениями. Этот подход основан на том, что многие матрицы, возникающие в задачах численного моделирования, обладают свойством близкой к ранговой недостаточности, то есть значительная часть информации может быть представлена меньшим числом главных компонент. Вместо хранения и обработки полной матрицы $A \in \mathbb{R}^{n \times m}$ , LRA позволяет оперировать двумя матрицами меньшего размера — $U \in \mathbb{R}^{n \times r}$ и $V \in \mathbb{R}^{r \times m}$ , где $r \ll \min(n, m)$ . Это существенно снижает требования к памяти и вычислительным ресурсам, особенно при работе с крупномасштабными задачами.

Метод аппроксимации низким рангом (LRA) существенно снижает требования к памяти и вычислительные затраты при работе с матрицей жесткости, являющейся ключевым компонентом при дискретизации стохастических дифференциальных уравнений в частных производных (SPDE). Матрица жесткости, возникающая в процессе численного решения SPDE, часто обладает свойством низкой ранговости, что позволяет эффективно представлять ее в виде произведения меньших матриц. Это приводит к значительному уменьшению объема необходимой памяти для хранения матрицы, а также снижает сложность операций, таких как решение систем линейных уравнений, используемых для вычисления решения SPDE. Снижение вычислительной сложности достигается за счет уменьшения размерности матричных операций, что особенно важно при работе с задачами высокой размерности.

Оценка точности аппроксимации низким рангом (LRA) осуществляется посредством среднеквадратичной ошибки восстановления (RMSRE). Величина RMSRE напрямую зависит от коэффициента сжатия данных τ и кумулятивного коэффициента энергии. Коэффициент сжатия τ определяет степень уменьшения размерности матрицы, а кумулятивный коэффициент энергии отражает долю сохраняемой информации. Важно отметить, что путём регулирования этих параметров возможно контролировать допустимый уровень погрешности восстановления, обеспечивая компромисс между точностью аппроксимации и вычислительными затратами.

Сравнение показывает, что разработанный решатель LRNS обеспечивает сходимость к референтному решению даже при значительном сжатии данных (например, при коэффициенте сжатия [latex] \tau = 88\% [/latex] и [latex] 10\% [/latex]). — Сравнение показывает, что разработанный решатель LRNS обеспечивает сходимость к референтному решению даже при значительном сжатии данных (например, при коэффициенте сжатия $\tau = 88\%$ и $10\%$ ).

LRNS: Гибридный Решатель для Эффективного Моделирования

Решатель LRNS (Low-Rank Neumann Series) объединяет преимущества аппроксимации низким рангом (LRA) и хорошо зарекомендовавшей себя эффективности ряда Неймана. Ряд Неймана представляет собой итеративный метод решения систем линейных уравнений, а использование LRA позволяет существенно снизить вычислительную сложность и требования к памяти при работе с большими матрицами, возникающими при дискретизации стохастических дифференциальных уравнений в частных производных (SPDE). Комбинация этих подходов позволяет эффективно аппроксимировать обратную матрицу дискретизированного оператора SPDE, обеспечивая существенное снижение вычислительных затрат и объема необходимой памяти по сравнению с традиционными методами.

Гибридный подход, используемый в LRNS Solver, обеспечивает эффективную аппроксимацию обратного дискретизированного оператора SPDE, что приводит к значительному снижению вычислительных затрат и требований к памяти. В ходе численных экспериментов было продемонстрировано, что данный метод позволяет уменьшить сложность вычислений по сравнению с традиционными подходами, особенно при решении крупномасштабных задач. Наблюдаемое сокращение вычислительной нагрузки и объема необходимой памяти позволяет решать задачи, которые ранее были недоступны из-за ограничений ресурсов.

Решение на основе LRNS эффективно использует операции с матрицей жесткости, опираясь на снижение размерности, достигаемое благодаря LRA (Low-Rank Approximation). Вместо непосредственной работы с полной матрицей жесткости, LRA позволяет представить её в виде произведения нескольких матриц меньшего размера, что значительно сокращает вычислительные затраты и требования к памяти. Это снижение размерности позволяет ускорить такие операции, как умножение матрицы на вектор, необходимые для решения системы линейных уравнений, возникающих при дискретизации SPDE (Stochastic Partial Differential Equation). Эффективность данного подхода напрямую зависит от способности LRA точно аппроксимировать исходную матрицу жесткости с минимальной потерей информации.

Показатели логарифмической ошибки решателя LRNS уменьшаются с увеличением усечения [latex]R[/latex] и масштабирования σ, что указывает на сходимость метода при различных значениях параметров. — Показатели логарифмической ошибки решателя LRNS уменьшаются с увеличением усечения $R$ и масштабирования σ, что указывает на сходимость метода при различных значениях параметров.

Математические Основы и Случайные Поля: Фундамент Моделирования

Анализ стохастических дифференциальных уравнений в частных производных (SPDE) невозможен без прочного базиса, предоставляемого пространствами Соболева. Эти функциональные пространства, обобщающие понятие дифференцируемости, позволяют строго определять свойства решений SPDE, даже если они не являются классически гладкими функциями. Пространства Соболева характеризуются порядком дифференцируемости и типом используемой нормы, что позволяет оценивать «регулярность» решений и доказывать их существование и единственность. Например, пространство $W^{k,p}(\Omega)$ описывает функции, первые $k$ производных которых принадлежат пространству $L^p(\Omega)$ . Использование пространств Соболева позволяет корректно ставить и решать задачи, возникающие в различных областях, таких как гидродинамика, квантовая механика и финансовая математика, где решения часто обладают ограниченной гладкостью или даже являются обобщенными функциями.

Случайные поля играют ключевую роль в моделировании стохастической природы стохастических дифференциальных уравнений в частных производных (СПДУ). В отличие от традиционных случайных процессов, зависящих от времени, случайные поля определены в пространстве, представляя собой набор случайных величин, каждой из которых соответствует определенная точка в пространстве. Это позволяет учитывать пространственную изменчивость неопределенностей, возникающих в различных физических явлениях, таких как турбулентность, распространение тепла или поведение финансовых рынков. Каждая точка пространства характеризуется определенным распределением вероятностей, что делает случайные поля мощным инструментом для описания сложных систем, где неопределенность не является однородной, а зависит от местоположения. Использование случайных полей позволяет строить более реалистичные и точные модели, учитывающие как случайные флуктуации, так и пространственную корреляцию между ними, что критически важно для прогнозирования и анализа сложных явлений.

Метод разделения возмущений представляет собой эффективный подход к анализу случайных полей, возникающих при исследовании стохастических дифференциальных уравнений в частных производных. Суть метода заключается в разложении сложного случайного поля на сумму более простых составляющих, каждая из которых описывает отдельное возмущение. Это позволяет значительно упростить анализ, поскольку вместо работы со сложным полем можно анализировать отдельные компоненты, что особенно полезно при получении приближенных решений. Разложение обычно основывается на выделении доминирующего члена и последующем рассмотрении остаточных возмущений как малой поправки. Такой подход не только облегчает математические вычисления, но и позволяет построить эффективные численные алгоритмы для приближенного решения соответствующих уравнений, что крайне важно в практических приложениях, таких как моделирование турбулентности или финансовые рынки. В результате, $ω(x) = ω_0(x) + εω_1(x)$ , где ε — малый параметр, описывающий вклад возмущения.

Представленное исследование демонстрирует стремление к математической точности в решении сложных дифференциальных уравнений в частных производных. Разработанный алгоритм LRNS, сочетающий в себе приближение низкого ранга и ряд Неймана, направлен на достижение детерминированной и воспроизводимой точности, что особенно важно при анализе систем с случайными коэффициентами. Как однажды заметил Эрвин Шрёдингер: «Нельзя говорить, что физика описывает реальность; она лишь описывает, что мы можем измерить об этой реальности». Эта фраза отражает суть подхода, представленного в статье: фокусировка на эффективном и точном решении уравнений, которые моделируют физические процессы, даже в условиях неопределенности, что позволяет получить надежные результаты для задач оптимального управления.

Что дальше?

Представленный подход, объединяющий приближение низкого ранга и ряд Неймана, демонстрирует снижение вычислительных издержек при решении нестационарных стохастических диффузионных уравнений. Однако, стоит признать, что элегантность решения не всегда гарантирует его универсальность. Вопрос о сходимости ряда Неймана для широкого класса коэффициентов остаётся открытым, и требуются более строгие доказательства корректности. Интуитивное ощущение «работы» алгоритма на тестовых примерах — недостаточная гарантия его надежности в произвольной ситуации.

Перспективным направлением представляется исследование возможности адаптивного выбора ранга приближения. Автоматическая оценка требуемой точности, основанная на анализе спектра оператора, позволила бы избежать избыточных вычислений и повысить эффективность алгоритма. Кроме того, следует обратить внимание на разработку методов оценки погрешности, не требующих знания точного решения — ведь в большинстве практических задач оно недоступно.

В конечном счёте, истинный прогресс в области численного моделирования стохастических процессов заключается не в увеличении скорости вычислений, а в повышении надёжности и обоснованности получаемых результатов. Любое приближение — это компромисс между точностью и вычислительными затратами, и задача исследователя — найти оптимальный баланс, опираясь не на эвристику, а на математическую строгость.

Оригинал статьи: https://arxiv.org/pdf/2601.11152.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-01-20 21:46