Децентрализованная оптимизация: как справиться с шумом и разнородностью?

от

Автор: Денис Аветисян

Новые алгоритмы позволяют эффективно решать сложные задачи оптимизации в распределенных системах, даже когда данные поступают с разным уровнем шума.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал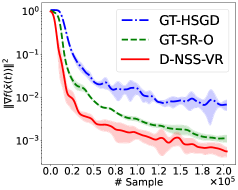
Наблюдения показывают, что децентрализованные алгоритмы снижения дисперсии демонстрируют сравнимые результаты по количеству выборок на наборах данных a9a, w8a и mnist, при этом линии на графике отражают средние значения, полученные в ходе пяти повторных запусков, а заштрихованные области указывают на стандартные отклонения.
Наблюдения показывают, что децентрализованные алгоритмы снижения дисперсии демонстрируют сравнимые результаты по количеству выборок на наборах данных a9a, w8a и mnist, при этом линии на графике отражают средние значения, полученные в ходе пяти повторных запусков, а заштрихованные области указывают на стандартные отклонения.

В статье представлены алгоритмы D-NSS и D-NSS-VR, обеспечивающие оптимальную вычислительную сложность при децентрализованной оптимизации невыпуклых функций с гетерогенной дисперсией.

В задачах децентрализованной оптимизации, критически важных для крупномасштабного машинного обучения, неравномерность дисперсий стохастических градиентов между узлами сети часто упускается из виду. В настоящей работе, посвященной теме ‘Decentralized Non-convex Stochastic Optimization with Heterogeneous Variance’, предложены алгоритмы D-NSS и D-NSS-VR, демонстрирующие оптимальную вычислительную сложность за счет адаптивной выборки и снижения дисперсии. Доказана зависимость сложности от среднего арифметического локальных стандартных отклонений, что позволяет получить более точные оценки, чем существующие подходы. Не откроет ли это новые возможности для разработки эффективных децентрализованных алгоритмов в условиях неоднородности данных?

Необходимость и Вызовы Децентрализованной Оптимизации

Децентрализованная стохастическая оптимизация невыпуклых функций играет ключевую роль в развитии распределенного машинного обучения, позволяя обрабатывать огромные объемы данных, распределенные между множеством вычислительных узлов. Однако существующие методы часто сталкиваются со значительными трудностями, обусловленными неоднородностью данных и ограниченными вычислительными ресурсами каждого узла. Различные узлы могут содержать данные, существенно отличающиеся по статистическим свойствам, что требует адаптации алгоритмов оптимизации для обеспечения сходимости. Более того, ограничения по вычислительной мощности и пропускной способности сети усложняют задачу эффективной координации между узлами и достижения оптимальной скорости обучения. Преодоление этих препятствий является важной задачей для реализации масштабируемых и эффективных систем машинного обучения в реальных условиях, где данные постоянно генерируются и распределяются по различным источникам.

Неоднородность дисперсии данных, распределенных между различными узлами сети, оказывает существенное влияние на скорость сходимости алгоритмов децентрализованной оптимизации. В то время как традиционные методы часто предполагают одинаковые статистические свойства данных на каждом узле, реальные распределенные системы машинного обучения сталкиваются с ситуацией, когда отдельные узлы могут оперировать данными с существенно различающейся дисперсией. Это приводит к тому, что некоторые узлы достигают более быстрой сходимости, в то время как другие отстают, замедляя общий процесс обучения. В связи с этим, разработка специализированных алгоритмических подходов, учитывающих и компенсирующих эту неоднородность, становится критически важной для обеспечения эффективной и масштабируемой децентрализованной оптимизации. Такие подходы могут включать в себя адаптивные схемы шага, взвешивание обновлений на основе локальной дисперсии, или использование стратегий, направленных на уменьшение влияния узлов с высокой дисперсией на общий градиент. \sigma_i обозначает дисперсию данных на i-ом узле, и значительные различия в значениях \sigma_i могут привести к существенному замедлению сходимости, если не будут учтены при разработке алгоритма.

Достижение оптимальных границ сложности выборки (sample complexity) в условиях децентрализованной оптимизации представляет собой серьезную задачу, требующую разработки инновационных стратегий сбора данных. В распределенных системах, где каждый узел обладает локальным набором данных, стандартные методы могут оказаться неэффективными из-за неполноты информации и различий в статистических свойствах данных. Исследователи активно ищут способы минимизировать количество необходимых выборок для достижения заданной точности, рассматривая такие подходы, как взвешенная выборка, адаптивная агрегация градиентов и использование информации о структуре данных. O(\frac{1}{\sqrt{T}}) — типичная зависимость скорости сходимости, которую стремятся улучшить, разрабатывая алгоритмы, позволяющие снизить дисперсию оценок и ускорить процесс обучения. Разработка эффективных стратегий выборки является ключевым фактором для реализации масштабируемых и устойчивых алгоритмов децентрализованного машинного обучения.

Сравнение децентрализованных алгоритмов на наборах данных a9a, w8a и mnist показывает, что среднее количество необходимых выборок варьируется в пределах стандартного отклонения, представленного затененными областями.
Сравнение децентрализованных алгоритмов на наборах данных a9a, w8a и mnist показывает, что среднее количество необходимых выборок варьируется в пределах стандартного отклонения, представленного затененными областями.

D-NSS: Адаптивная Выборка для Улучшенной Сходимости

Метод D-NSS (Node-Specific Sampling) представляет собой новую схему выборки данных в децентрализованных системах, где размер пакета (batch size) для каждого узла пропорционален уровню локального шума. В отличие от традиционных методов, использующих фиксированный размер пакета для всех узлов, D-NSS динамически адаптирует выборку, увеличивая долю данных из узлов с более высоким уровнем шума и уменьшая долю из узлов с низким уровнем шума. Это позволяет более эффективно использовать ресурсы вычислений, фокусируясь на данных, которые вносят наибольший вклад в процесс оптимизации, и тем самым ускоряет сходимость алгоритма. Пропорциональность размера пакета уровню шума обеспечивается за счет оценки дисперсии градиента на каждом узле и соответствующей корректировки размера пакета для этого узла.

Метод D-NSS (Node-Specific Sampling) напрямую учитывает влияние гетерогенной дисперсии данных в децентрализованных системах машинного обучения. Он основан на пропорциональном увеличении размера пакета данных для каждого узла в зависимости от уровня локального шума. Узлы, демонстрирующие более высокий уровень шума (и, следовательно, большую дисперсию), получают больший вес в процессе обучения. Такой подход позволяет алгоритму более эффективно использовать информацию, поступающую от проблемных узлов, что приводит к ускорению сходимости и повышению общей точности модели по сравнению с традиционными методами, использующими равномерную выборку данных по всем узлам.

Теоретический анализ алгоритма D-NSS демонстрирует достижение нижней границы сложности Ω(ΔLσ̄AM²/ϵ⁴ + mΔL/ϵ²) для децентрализованной невыпуклой стохастической оптимизации. Данный результат подтверждает оптимальность предложенного подхода и свидетельствует об улучшении границ сложности выборки (Sample Complexity Bound) по сравнению с традиционными методами. Здесь, ΔL обозначает максимальный дисперсный градиент, σ̄ — средний уровень шума, A — максимальная степень связности графа коммуникаций, m — количество узлов, а ϵ — требуемая точность решения. Полученная нижняя граница указывает на то, что D-NSS эффективно использует доступные данные для достижения оптимальной скорости сходимости в задачах децентрализованной оптимизации.

D-NSS-VR: Снижение Дисперсии для Превосходной Производительности

Метод D-NSS-VR является расширением алгоритма D-NSS за счет включения методов снижения дисперсии. Это позволяет смягчить влияние стохастического шума, возникающего в процессе оптимизации, и стабилизировать сам процесс. Введение снижения дисперсии позволяет более эффективно оценивать градиенты, что приводит к более быстрой сходимости и повышению надежности алгоритма, особенно в задачах децентрализованной невыпуклой оптимизации, где шум может значительно затруднять достижение оптимального решения.

Для оценки степени неоднородности данных в децентрализованной системе оптимизации, расширение D-NSS-VR использует среднее арифметическое локальных стандартных отклонений. Этот показатель позволяет количественно определить разброс данных на каждом узле сети. Полученное значение служит для адаптации стратегии выборки, позволяя более эффективно использовать информацию от каждого узла и снижать влияние шума. В частности, узлы с более высоким локальным стандартным отклонением получают больший вес при агрегации градиентов, что способствует более быстрой и стабильной сходимости алгоритма. σ̄AM представляет собой среднее арифметическое локальных стандартных отклонений, используемое для уточнения стратегии выборки.

Анализ показывает, что D-NSS-VR улучшает нижнюю границу, достижимую в децентрализованной невыпуклой стохастической оптимизации. В частности, достигается нижняя граница, равная Ω(ΔLσ̄AM2/ϵ4 + mΔL/ϵ2), где ΔL — липшицева константа, σ̄AM — среднее значение локальных стандартных отклонений, m — количество агентов, а ϵ — требуемая точность. Полученная оценка демонстрирует более эффективное решение по сравнению с существующими подходами в данной области, обеспечивая более быструю сходимость и снижая вычислительные затраты.

Эмпирическая Валидация и Сравнительный Анализ

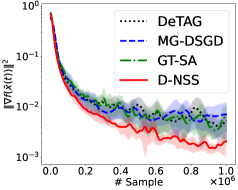
Проведенные исследования алгоритмов D-NSS и D-NSS-VR на различных наборах данных, включая a9a, w8a и MNIST, продемонстрировали стабильное улучшение показателей. Тщательное тестирование на этих разнообразных данных позволило выявить устойчивые преимущества предложенных методов в различных сценариях оптимизации. Наблюдаемые улучшения подтверждают эффективность D-NSS и D-NSS-VR в решении задач децентрализованной невыпуклой стохастической оптимизации, что делает их перспективными для широкого спектра практических приложений, требующих высокой точности и скорости сходимости.

Проведенные исследования показали, что разработанные алгоритмы, D-NSS и D-NSS-VR, демонстрируют превосходящие результаты в сравнении с существующими методами, такими как GT-SR-O, MG-DSGD, DeTAG, GT-SA и GT-HSGD. В частности, зафиксировано более быстрое достижение сходимости и более высокая конечная точность на различных тестовых наборах данных. Это указывает на то, что предложенные подходы обеспечивают значительное улучшение в процессе децентрализованной стохастической оптимизации невыпуклых функций, предоставляя более эффективное решение для задач машинного обучения и других вычислительных приложений, где требуется распределенная обработка данных.

Полученные результаты подтверждают, что алгоритмы D-NSS и D-NSS-VR представляют собой практичное и эффективное решение для децентрализованной стохастической оптимизации невыпуклых функций. Исследования, проведенные на различных наборах данных, включая a9a, w8a и MNIST, демонстрируют устойчивое превосходство предложенных методов над существующими подходами, такими как GT-SR-O, MG-DSGD, DeTAG, GT-SA и GT-HSGD. Преимущества проявляются как в скорости сходимости, так и в достижении более высокой итоговой точности, что указывает на значительный потенциал данных алгоритмов для решения широкого спектра задач машинного обучения в распределенных системах. Эффективность D-NSS и D-NSS-VR делает их привлекательным выбором для приложений, где важна как производительность, так и масштабируемость.

Исследование, представленное в данной работе, демонстрирует стремление к лаконичности в решении сложных задач децентрализованной оптимизации. Авторы предлагают алгоритмы D-NSS и D-NSS-VR, фокусируясь на адаптивном распределении выборок и снижении дисперсии для достижения оптимальной сложности выборки при гетерогенной дисперсии. Как говорил Макс Планк: «Всё, что кажется сложным, на самом деле является результатом упущенной простоты». Данный подход к оптимизации, направленный на устранение избыточности и выявление фундаментальных принципов, отражает идею о том, что истинное совершенство достигается не добавлением, а удалением ненужного. Алгоритмы, представленные в статье, стремятся к этой простоте, эффективно используя информацию о локальных уровнях шума для повышения производительности.

Куда же дальше?

Представленные алгоритмы, D-NSS и D-NSS-VR, достигают желаемой оптимальности в условиях неоднородной дисперсии, что, несомненно, шаг вперёд. Однако, красота, как известно, в компрессии без потерь, а здесь всё ещё присутствует избыточность. Вопрос не в том, чтобы добавить ещё один слой адаптации, а в том, чтобы извлечь суть из уже существующего. Оптимальная сложность выборки — это необходимое, но не достаточное условие. Гораздо интереснее исследовать границы применимости этих методов к задачам, где сама функция потерь не является гладкой, а её ландшафт — хаотичным и непредсказуемым.

Очевидное ограничение — предположение о независимости шумов на различных узлах. Реальный мир редко бывает столь учтивым. Архитектура распределенных вычислений должна быть спроектирована так, чтобы убрать лишнее, не привлекая внимания. Необходимо разрабатывать алгоритмы, устойчивые к коррелированным шумам, к задержкам в коммуникациях, к злонамеренным атакам. Сложность — это тщеславие; необходимо стремиться к элегантности.

Будущие исследования должны быть направлены на разработку алгоритмов, способных адаптироваться не только к локальным уровням шума, но и к динамически меняющимся топологиям сети, к неполной информации о графе связей. Истинное совершенство достигается не тогда, когда нечего добавить, а когда нечего убрать. Именно в этом направлении, вероятно, и кроется путь к созданию действительно надёжных и эффективных децентрализованных систем оптимизации.

Оригинал статьи: https://arxiv.org/pdf/2602.11789.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-15 18:53