Динамические системы и вмешательства: новый подход к точному прогнозированию

Автор: Денис Аветисян

Исследователи предлагают гибридную модель, сочетающую теоретические знания и анализ данных, для более надежной оценки эффектов от различных воздействий на сложные системы.

"Покупай на слухах, продавай на новостях". А потом сиди с акциями никому не известной биотех-компании. Здесь мы про скучный, но рабочий фундаментал.

Бесплатный Телеграм канал

Гибридная модель, сочетающая механистический подход и анализ данных, использует двухэтапный процесс обучения: на первом этапе создаются синтетические данные на основе известной механистической модели для обучения энкодера, сопоставляющего траектории состояния и вмешательства с вектором параметров с использованием среднеквадратичной ошибки [latex]MSE[/latex], а на втором этапе, при фиксированном энкодере, обучаются корректирующие сети на исходном наборе данных, оптимизируя [latex]MSE[/latex] между наблюдаемыми и реконструированными сигналами. — Гибридная модель, сочетающая механистический подход и анализ данных, использует двухэтапный процесс обучения: на первом этапе создаются синтетические данные на основе известной механистической модели для обучения энкодера, сопоставляющего траектории состояния и вмешательства с вектором параметров с использованием среднеквадратичной ошибки $MSE$ , а на втором этапе, при фиксированном энкодере, обучаются корректирующие сети на исходном наборе данных, оптимизируя $MSE$ между наблюдаемыми и реконструированными сигналами.

Представлен структурированный гибридный механистический подход для устойчивой оценки результатов временных интервенций в динамических системах, объединяющий причинно-следственный вывод и коррекцию на основе данных.

Оценка эффектов вмешательств в динамических системах представляет собой сложную задачу, особенно при экстраполяции за пределы доступных данных. В работе ‘Structured Hybrid Mechanistic Models for Robust Estimation of Time-Dependent Intervention Outcomes’ предложен гибридный подход, сочетающий механистические модели с компонентами, обучаемыми на данных, для более точной оценки временных эффектов вмешательств. Предложенная структура позволяет использовать априорные знания о системе, одновременно корректируя их на основе наблюдаемых данных, что обеспечивает повышенную надежность прогнозов в различных условиях. Может ли подобный подход открыть новые возможности для оптимизации вмешательств в сложных, реальных динамических системах, где полная информация о механизмах часто недоступна?

Пределы Механистического Моделирования

Традиционные механистические модели, основанные на обыкновенных дифференциальных уравнениях (ОДУ), демонстрируют высокую эффективность в описании систем, где физические законы известны и четко определены. Однако, применительно к сложным, реальным системам, эти модели сталкиваются с существенными ограничениями. Сложность заключается в том, что многие природные явления характеризуются нелинейностью, хаотичностью и взаимодействием множества факторов, которые трудно или невозможно точно учесть в рамках ОДУ. Это приводит к тому, что даже незначительные погрешности в исходных данных или неполное описание процессов могут существенно исказить результаты моделирования, ограничивая ее прогностическую способность и практическую ценность. В то время как ОДУ хорошо подходят для идеализированных сценариев, их применение к реальным системам требует значительных упрощений и компромиссов, что часто снижает адекватность модели.

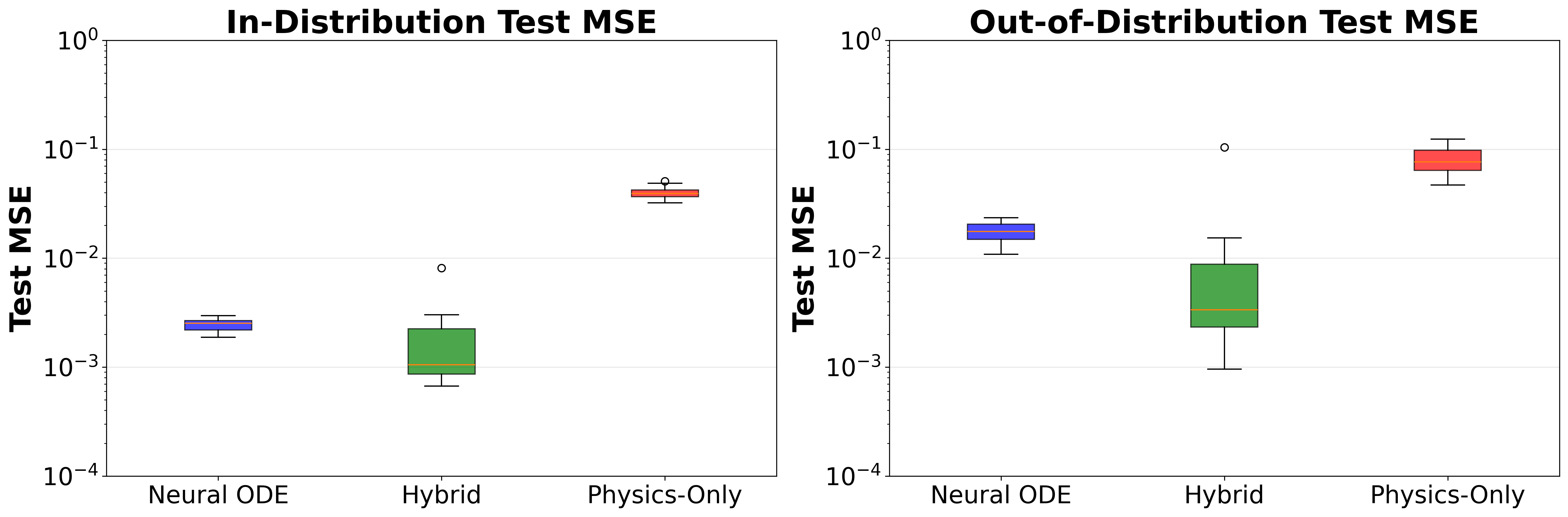
Традиционные механистические модели, основанные на обыкновенных дифференциальных уравнениях, часто сталкиваются с проблемой точности параметров. Для корректной работы им требуется детальное знание всех базовых величин, что на практике встречается крайне редко. Неточность или отсутствие информации о параметрах неизбежно приводит к погрешностям и снижает прогностическую способность модели. В отличие от этого, разработанная гибридная модель демонстрирует повышенную устойчивость к неопределенности параметров, что подтверждается более низким значением среднеквадратичной ошибки реконструкции (Test Reconstruction MSE) в динамике маятника, как показано на рисунке 3. Это позволяет добиться более точных и надежных прогнозов даже в условиях неполной информации, превосходя как чисто эмпирические, так и исключительно механистические подходы.

Тесты реконструкции траекторий маятника показали, что средняя квадратичная ошибка (MSE) при прогнозировании траекторий из случайных начальных условий и параметров, полученных из обучающей выборки, значительно различается для внутрираспределительных и внераспределительных типов воздействий, что указывает на чувствительность модели к изменениям в данных.

Преодолевая Разрыв: Коррекция на Основе Данных

Гибридный подход, объединяющий механистические модели с компонентами коррекции на основе данных, представляет собой эффективное решение для преодоления ограничений, присущих исключительно механистическому моделированию. Механистические модели, хотя и основаны на фундаментальных принципах, часто не могут учесть всю сложность реальных систем из-за упрощений и неполноты знаний. Компоненты коррекции на основе данных, такие как нейронные сети, способны изучать и компенсировать расхождения между моделью и наблюдаемыми данными, тем самым повышая точность и надежность прогнозов. Такой подход позволяет использовать преимущества обоих методов — принципиальной обоснованности механистических моделей и способности к обучению и адаптации, характерной для методов машинного обучения.

Нейронные сети, в особенности Neural ODE (Ordinary Differential Equations), демонстрируют высокую эффективность в обучении остаточным динамическим характеристикам, не отраженным в механистических моделях. В отличие от традиционных нейронных сетей, Neural ODE моделируют динамику как непрерывный процесс, что позволяет им эффективно аппроксимировать сложные зависимости во временных рядах данных. Это достигается за счет обучения функции, описывающей производную состояния системы, а не дискретных изменений между временными точками. В результате, использование Neural ODE в качестве компонента коррекции позволяет значительно повысить точность и устойчивость механистических моделей, особенно в задачах, где остаточные ошибки могут накапливаться со временем и приводить к существенным отклонениям от реальных данных.

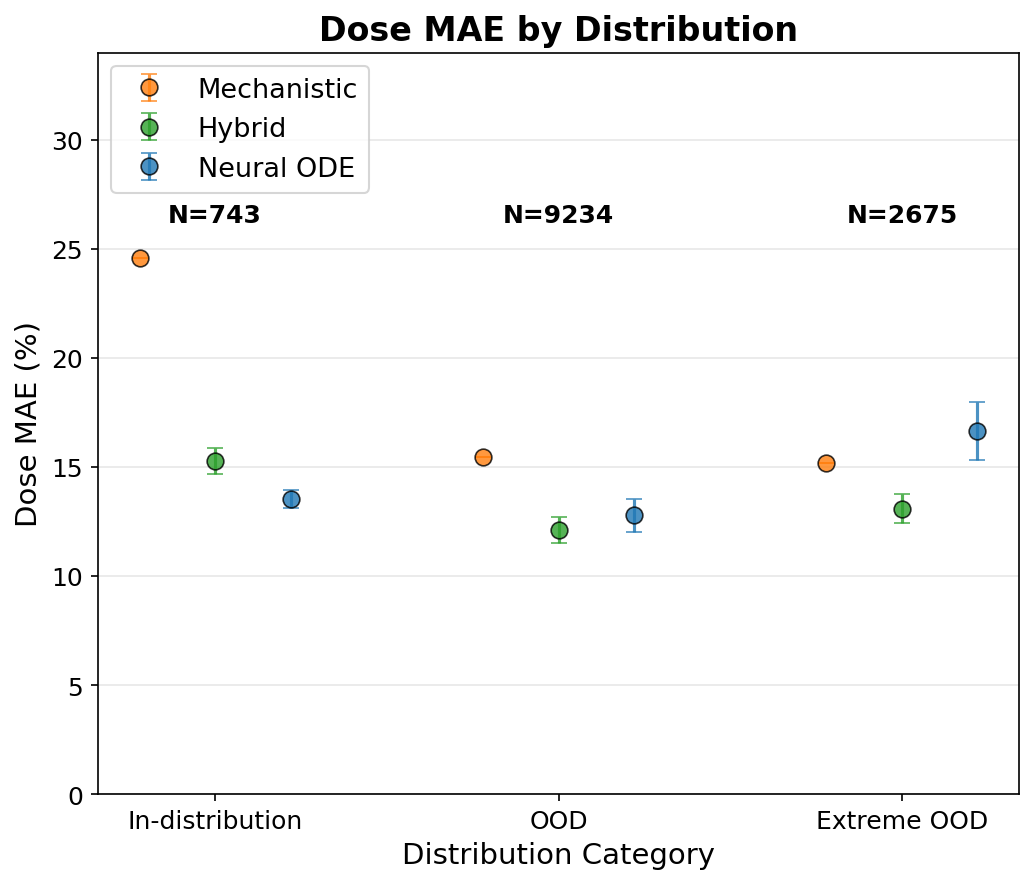
Для повышения эффективности обучения моделей, использующих временные ряды данных, применялись методы Window-Based Training и Batch Training. Window-Based Training позволяет моделировать динамику данных в локальном временном окне, что улучшает адаптацию к нелинейным зависимостям. Batch Training, в свою очередь, оптимизирует процесс обучения за счет обработки данных пакетами, снижая вычислительные затраты. В результате применения данных методов в нашей фармакокинетической (PK) модели, была достигнута более низкая средняя абсолютная процентная ошибка (MDAPE) по сравнению с базовыми моделями, что наглядно демонстрируется на рисунке 5. Полученные данные свидетельствуют о значительном улучшении точности прогнозирования PK модели при использовании гибридного подхода.

Результаты PK-теста показывают, что средняя абсолютная процентная ошибка (MAPE) варьируется в зависимости от группы пациентов: в распределении, вне распределения (возраст > 60 или ИМТ > 30) и экстремально вне распределения (возраст > 60 и ИМТ > 30), при этом оценка механистической модели Schnider et al. (1998) проводилась на основе данных 24 пациентов в возрасте от 26 до 81 года.

Учёт Внешних Воздействий: Гибкость Модели

В реальных системах динамика часто подвергается воздействию временных интервенций — событий, изменяющих параметры системы во времени. Это требует разработки моделей, способных адекватно учитывать влияние этих изменений на прогнозируемые значения. Традиционные модели, предполагающие стационарность параметров, могут давать неточные результаты при наличии таких интервенций. Необходимость точного учета временной зависимости интервенций особенно актуальна в задачах прогнозирования и управления, где даже небольшие погрешности могут приводить к значительным отклонениям от целевых значений. Для решения этой задачи используются модели, способные динамически адаптироваться к изменяющимся условиям и учитывать временной лаг между интервенцией и ее проявлением в данных.

Наш гибридный подход обеспечивает точное прогнозирование в различных условиях за счет интеграции как независимых от вмешательств, так и зависимых от них корректировок. Независимые корректировки учитывают базовые системные характеристики, остающиеся неизменными при внешних воздействиях. Зависимые корректировки, в свою очередь, моделируют изменения, вызванные конкретными вмешательствами, что позволяет учитывать их влияние на динамику системы. Комбинирование этих двух типов корректировок позволяет модели адаптироваться к изменяющимся условиям и обеспечивать более точные результаты по сравнению с подходами, учитывающими только один из этих факторов. Это особенно важно в системах, подверженных частым и разнообразным внешним воздействиям, где стандартные модели могут давать значительные погрешности.

Для повышения точности механической модели используется сеть-энкодер, которая выполняет инференс неизвестных параметров на основе наблюдаемых данных. Этот процесс позволяет уточнить параметры модели, которые не могут быть определены напрямую из априорных знаний или предварительных измерений. Сеть-энкодер обучается на исторических данных, выявляя взаимосвязи между наблюдаемыми переменными и скрытыми параметрами модели. В результате, модель становится более адаптивной к различным условиям и способна точнее предсказывать поведение системы, улучшая общую достоверность и надежность прогнозов.

Среднеквадратичная ошибка (MSE) и стандартная ошибка среднего (SEM) при предсказании исхода вмешательства для трех моделей демонстрируют зависимость от расстояния до обучающего набора вмешательств, представленную в логарифмической шкале.

Применение в Фармакокинетике и За её Пределами

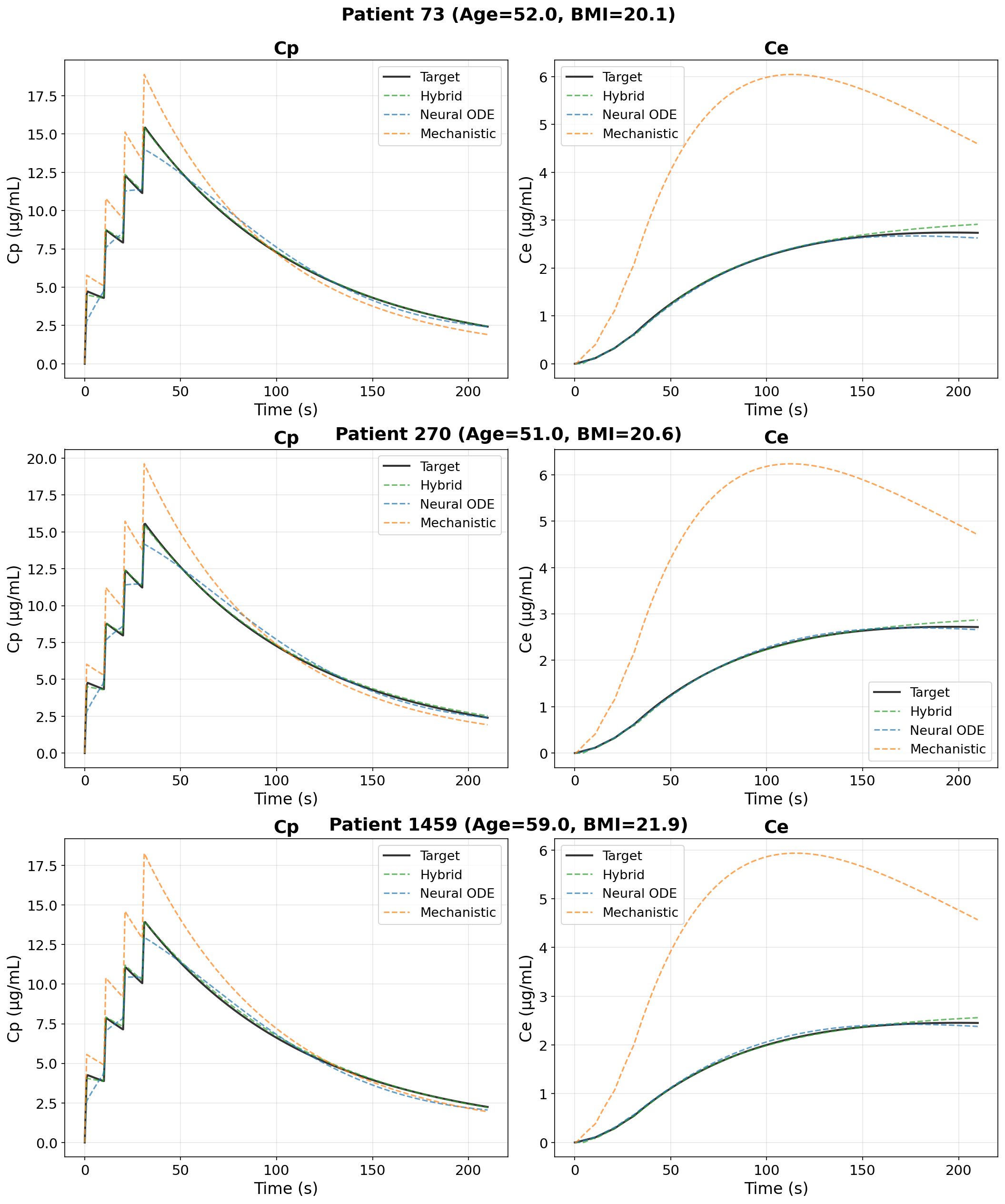
Исследование демонстрирует высокую эффективность предложенного гибридного подхода посредством анализа фармакокинетики — науки о том, как организм обрабатывает лекарственные препараты. Точное моделирование поведения лекарств в организме стало возможным благодаря сочетанию различных математических методов и алгоритмов. В ходе работы была показана способность модели адекватно предсказывать концентрацию препарата в крови и тканях во времени, что критически важно для определения оптимальной дозировки и режима приема лекарств. Полученные результаты подтверждают перспективность применения данной методологии не только в фармакологии, но и в других областях, где необходимо анализировать и прогнозировать динамические процессы.

Включение мышечной массы тела (Lean Body Mass, LBM) в фармакокинетические (PK) модели позволяет значительно повысить точность прогнозирования поведения лекарственных препаратов в организме. Традиционные модели часто используют общий вес тела, что может приводить к неточностям, поскольку распределение и метаболизм лекарств тесно связаны с количеством мышечной ткани. Учет LBM, как ключевого параметра, позволяет более адекватно отразить физиологические особенности пациента, влияющие на фармакокинетику, что особенно важно при разработке индивидуальных схем лечения и оптимизации дозировок. Данный подход позволяет более точно предсказывать концентрацию препарата в крови, время его полувыведения и другие важные фармакокинетические параметры, что, в свою очередь, способствует повышению эффективности и безопасности лекарственной терапии.

Предложенный методологический подход не ограничивается областью фармакокинетики и обладает значительным потенциалом для моделирования широкого спектра динамических систем. Исследования показали, что та же математическая структура, успешно примененная для анализа поведения лекарственных препаратов в организме, может быть эффективно использована для описания, например, колебаний математического маятника. Гибкость данной системы позволяет адаптировать её к различным физическим и биологическим процессам, открывая новые возможности для научных исследований и прогнозирования поведения сложных систем. Способность моделировать динамику различных явлений делает её универсальным инструментом для учёных, работающих в самых разных областях науки.

Модель точно предсказывает динамику фармакокинетики пропофола.

Исследование, представленное в данной работе, стремится к созданию моделей, способных надежно оценивать эффекты вмешательств в динамических системах. Этот подход, объединяющий механистические и основанные на данных компоненты, подчеркивает важность лаконичности и точности. В связи с этим, уместно вспомнить слова Дональда Кнута: «Оптимизм — это вера в то, что все будет хорошо; пессимизм — знание, что это так». Данная фраза отражает суть работы: стремление не просто предсказывать, но и обеспечивать надежность предсказаний, особенно в условиях неопределенности и экстраполяции, что является ключевой задачей в оценке временных эффектов вмешательств. Простота и ясность моделирования, в конечном итоге, обеспечивают более устойчивые и достоверные результаты.

Что дальше?

Предложенный подход, объединяющий механистические модели и коррекцию на основе данных, не является, конечно, окончательным ответом. Скорее, он обнажает главное — уязвимость любой попытки предсказания в динамических системах. Осознание этого — первый шаг к созданию действительно надежных инструментов. Проблема не в усложнении моделей, а в их радикальном упрощении. Система, требующая подробной инструкции, уже проиграла.

Ключевым направлением дальнейших исследований представляется не столько повышение точности оценок, сколько разработка метрик, позволяющих оценивать надежность предсказаний в условиях неопределенности. Необходимо стремиться к понятности — вежливости в науке. Чем сложнее модель, тем труднее определить, где кроется ее фундаментальная ошибка. Интервенционные эффекты, зависящие от времени, особенно уязвимы к таким ошибкам.

В конечном итоге, ценность предложенного подхода заключается не в конкретных алгоритмах, а в сдвиге парадигмы. Необходимо признать, что идеальная модель — это не та, которая учитывает все факторы, а та, от которой можно отказаться, не потеряв существенной информации. Понятие, которое можно передать без объяснений — вот к чему стоит стремиться.

Оригинал статьи: https://arxiv.org/pdf/2602.11350.pdf

Связаться с автором: https://www.linkedin.com/in/avetisyan/

Смотрите также:

2026-02-14 14:12